sistema-de-unidades-la-energia-y-su

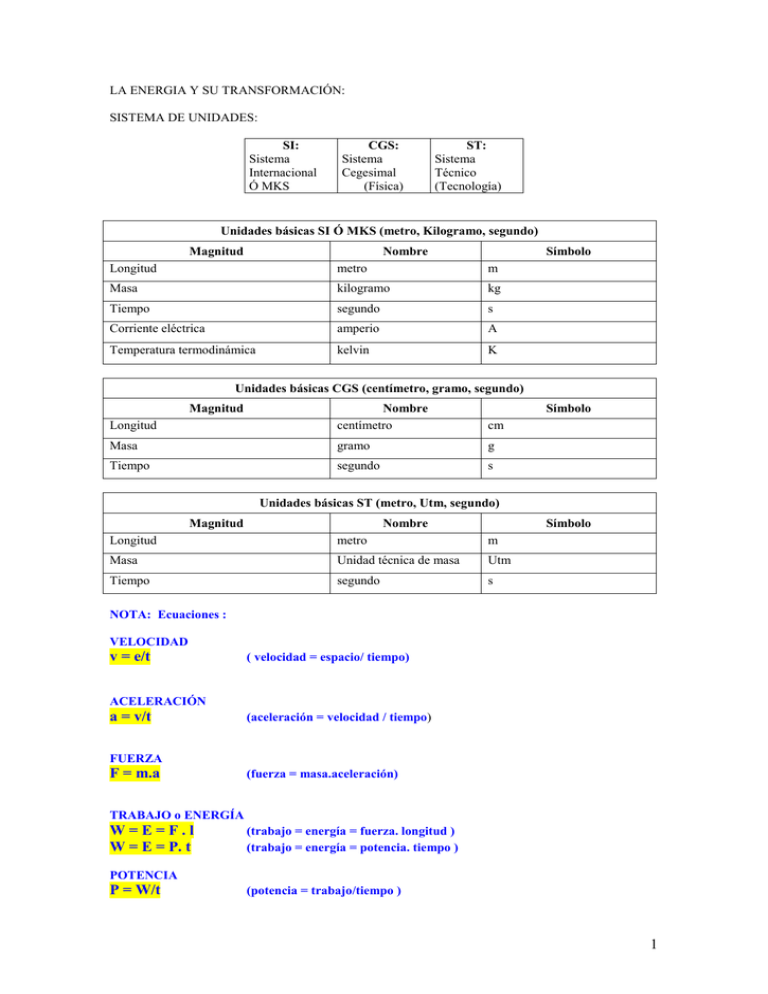
LA ENERGIA Y SU TRANSFORMACIÓN:
SISTEMA DE UNIDADES:
SI:
Sistema
Internacional
Ó MKS
CGS:
Sistema
Cegesimal
(Física)
ST:
Sistema
Técnico
(Tecnología)
Unidades básicas SI Ó MKS (metro, Kilogramo, segundo)
Magnitud
Nombre
Símbolo
Longitud
metro
m
Masa
kilogramo
kg
Tiempo
segundo
s
Corriente eléctrica
amperio
A
Temperatura termodinámica
kelvin
K
Unidades básicas CGS (centímetro, gramo, segundo)
Longitud
Magnitud
Nombre
centímetro
cm
Símbolo
Masa
gramo
g
Tiempo
segundo
s
Unidades básicas ST (metro, Utm, segundo)
Magnitud
Nombre
Símbolo
Longitud
metro
m
Masa
Unidad técnica de masa
Utm
Tiempo
segundo
s
NOTA: Ecuaciones :
VELOCIDAD
v = e/t
( velocidad = espacio/ tiempo)
ACELERACIÓN
a = v/t
(aceleración = velocidad / tiempo)
FUERZA
F = m.a
(fuerza = masa.aceleración)
TRABAJO o ENERGÍA
W=E=F.l
W = E = P. t
(trabajo = energía = fuerza. longitud )
(trabajo = energía = potencia. tiempo )
POTENCIA
P = W/t
(potencia = trabajo/tiempo )
1
Magnitud
Longitud
Masa
Tiempo
Velocidad
lineal
Aceleración
Lineal
Superficie
Volumen
Densidad
Fuerza
Unidades derivadas
Ecuación
CGS
SI
dimensional
L
cm
m
M
g
Kg
T
s
s
m
Utm
s
1m=100cm
1Utm=9,8kg=9800g
L·T-1
cm/s
m/s
m/s
1m/s=100cm/s
L·T-2
cm/s2
m/s2
m/s2
1 m/s2=100 cm/s2
L2
L3
M·L-3
M·L T-2
cm2
cm3
g/cm3
dina=gcm/s2
m2
m3
kg/m3
Newton=
kg·m/s2
m2
m3
Utm/m3
kg-fuerza=
Kilopondio=
Utm m/ s2
1 m2=104cm2
1m3=106 cm3
1 kg/m3=10-3g/cm3
1kp=9,8N=
1 N=105dinas
1kp= 9,8·105dinas
ST
Equivalencias
1 dina=1,02·10-6 Kp
Presión
M·L-1 T-2
baria=dina/cm2
Trabajo
M·L2 T-2
ergio=dina.cm
P=N/m2
Pascal
J=N.m
Potencia
M·L2 T-3
ergio/s
W=J/s
kg/m2
kp.m=kg.m
kilogrametro
kg.m/s
1 bar= 1,02 kp/cm2
1kp/cm2=1atm=105P
1kg.m = 9,8J
1J=107ergios
1kg.m/s=9,8W=
9,8.107ergios/s
Otras equivalencias:
1CV=75kg.m/s=75kg.9,8N/kg.m/s=735W
1 Wh =3600J
1 cal = 4,18 J
Magnitud
Longitud
Masa
Tiempo
Resumen Equivalencias
CGS
SI
cm
m
g
Kg
s
s
Velocidad
Aceleración
Fuerza
cm/s
cm/s2
dina=gcm/s2
m/s
m/s2
Newton=
kg·m/s2
Presión
baria=dina/cm2
Trabajo
ergio=dina.cm
P=N/m2
Pascal
J=N.m
Potencia
ergio/s
W=J/s
ST
m
Utm
s
m/s
m/s2
Kilopondio = kgfuerza= =
Utm m/ s2
kg/m2
kp.m=kg.m
kilogrametro
kg.m/s
2
Demostración de equivalencias:
LONGITUD
1m = 100cm
MASA
1 Utm = 9,8 Kg = 9800 g
VELOCIDAD
(v = e/t )
1m/s = 100cm/s
ACELERACIÓN
(a = v/t )
1m/ s2 = 100cm/s2
FUERZA
(F = m.a )
1N = 1Kg.m/s2
1kp= 9,8N
1Kp = 1Utm.m/s2 = 9,8 Kg. m/s2 =9,8N
1 N = 105 dinas
1 N = 1Kg.m/s2 = 1000g.100cm/s2 =105dinas
1kp= 9,8·105dinas
1Kp = 1Utm.m/s2 = 9,8 Kg. m/s2 = 9,8.1000g.100cm/s2 =9,8·105dinas
1 dina=1,02·10-6Kp
1Kp = 9,8·105dinas; 1dina = 1/9,8. 105Kp = 1,02·10-6 Kp
TRABAJO o ENERGÍA
( W = E = F . l ) ( W = E = P. t)
1J = 1 N.m
1kp.m = 9,8J
1Kp.m = 9,8N.m =9,8J
1 J = 107ergios
1 J = 1N.m = 1Kg.m/s2 .m = 1000g.100cm /s2 .100cm = 107dina.cm = 107ergios
1kp.m =9,8.107ergios
1kg.m = 9,8N.m = 9,8Kg.m/s2 .m = 9,8.1000g.1002cm2 /s2 = 9,8. 107dina.cm = 9,8.107ergios
POTENCIA
( P = W/t )
1W = 1J/s
1kp.m/s=9,8W
1kp.m/s=9,8N. m/s = 9,8 J/s = 9,8 W
1W = 107ergios /s
1W = 1 J/s = 1N.m/s = 1Kg.m/s2 .m/s = 1000g.100cm /s2 .100cm/s = 107dina.cm /s = 107ergios /s
1kp.m/s =9,8.107ergios /s
1kg.m/s = 9,8N.m/s = 9,8Kg.m/s2 .m/s = 9,8.1000g.1002cm2 /s2 /s = 9,8. 107dina.cm/s = 9,8.107ergios /s
3
Ejercicios:
1.- Si una persona decimos que pesa 70Kg ¿Cuántos newtons (N) pesa?
2.- Expresa las unidades de fuerza, trabajo y potencia en función de las unidades básicas en el Sistema
Internacional y en el Sistema Cegesimal.
3.- ¿ Cuántos Ws hay en 1000 J?
4.- ¿Cuántos Wh son 10800J?
5.- Si en la factura de la luz nos llega un consumo de 550KWh ¿cuántos julios son?
6.- ¿Cuántos kg hay en una Utm?
7.- ¿Qué unidades son obtenidas de las unidades fundamentales?
8.- En qué disciplinas se utilizan el Sistema CGS y el ST?
9.- ¿Cuál de los tres sistemas tiene menor peso? ¿Y mayor peso?
10.- ¿Cuántos CV tiene un compresor de 2800W?
11.- Si un motor de 20 CV ha estado funcionando durante 5h, calcula la energía consumida en KWh.
4
SOLUCIONES
Ejercicios:
1.- Si una persona decimos que pesa 70Kg ¿Cuántos newtons (N) pesa?
P = 70 Kg.9,8N/Kg = 700N
2.- Expresa las unidades de fuerza, trabajo y potencia en función de las unidades básicas en el Sistema
Internacional y en el Sistema Cegesimal.
1N = 1 Kg.m/s2
1J = 1N.m = 1 Kg.m/s2.m = 1 Kg.m2/s2
1W = 1J/s = 1 Kg.m2/s3
3.- ¿ Cuántos Ws hay en 1000 J?
1Ws =1J
1000 J = 1000Ws
4.- ¿Cuántos Wh son 10800J?
E = 10800 J = 10800 W.s = 10800 W s 1h/3600s = 3 Wh
5.- Si en la factura de la luz nos llega un consumo de 550KWh ¿cuántos julios son?
E = 550KWh = 550KWh.3600s/1h = 1,98.10 9 J
6.- ¿Cuántos kg hay en una Utm?
9,8 Kg
7.- ¿Qué unidades son obtenidas de las unidades fundamentales?
Las unidades derivadas
8.- En qué disciplinas se utilizan el Sistema CGS y el ST?
ST: TECNOLOGÍA
CGS: FÍSICA
9.- ¿Cuál de los tres sistemas tiene menor peso? ¿Y mayor peso?
Menor: CGS
Mayor: ST
10.- ¿Cuántos CV tiene un compresor de 2800W?
P = 2800W . 1CV/735 W = 3,8CV
11.- Si un motor de 20 CV ha estado funcionando durante 5h, calcula la energía consumida en KWh.
E = P.t = 20 CV. 735 W / 1CV . 5h = 2940 Wh = 2,94 KWh
5
TIPOS DE ENERGÍA
ENERGÍA es la capacidad q tiene un cuerpo o sistema para efectuar un trabajo.
Energía cinética y potencial. Energía mecánica
Energía cinética es la energía que posee un cuerpo debido a su velocidad: Ec = 1/2mv2
Energía potencial es la energía que posee un cuerpo debido a su posición dentro de un campo de fuerzas:
Ep = mgh
Energía mecánica es la suma de energías cinética y potencial:
Em = Ec + Ep
Si no existe rozamiento:
∆Em = 0
Em2 - Em1 = 0
Em2 = Em1
Ec2 + Ep2 = Ec1 + Ep1
Cálculo de la velocidad al soltar un cuerpo desde una altura h1:
Ec1 = 0 porque v1 = 0
Ep2 = 0 porque h2 = 0
Luego :
Ec2 + Ep2 = Ec1 + Ep1
1/2mv22 = mgh1
v2 =
2gh1
NOTA: Em1 = Em2 =Em3
1
2
3
PUNTO1
Ec = 0 v = 0
Em = Ep =mgh
PUNTO 2
Ec = 1/2mv2
2 g (h1  h2)
Ep =mgh2
v=
PUNTO 3
Ec = 1/2mv2
v=
2gh1
Ep =0
Em = Ec
La velocidad en este
caso es la diferncia
de alturas.
La Ep se calcula con
la altura en ese punto
Ejercicio
Se deja caer un cuerpo que pesa 83 Kg desde una altura de 60 m. Calcula la energía cinética, potencial y
mecánica en los siguientes puntos:
a) Cuando está a punto de caer.
b) Cuando está a dos tercios de la altura total.
c) En el instante anterior a llegar al suelo.
6
SOLUCION
Ejercicio
Se deja caer un cuerpo que pesa 83 Kg desde una altura de 60 m. Calcula la energía cinética, potencial y
mecánica en los siguientes puntos:
a) Cuando está a punto de caer.
b) Cuando está a dos tercios de la altura total.
c) En el instante anterior a llegar al suelo.
a)
Ec = 0 v = 0
Em = Ep =mgh = 83 Kg .9,8 m/s2 . 60m = 48.804 J
b) h2 = 40m
Ec2 = 1/2mv2
Cálculo de v:
Ec2 + Ep2 = Ec1 + Ep1
1/2mv22 +mgh2 = mgh1
v=
2 g (h1  h2) =
2.9,8.(60  40) m/s = 19,79 m/s
Ec2 = 1/2mv2 = 16.268 J
Ep2= mgh2 = 83 Kg 9,8m/s2 40m = 32.536 J
Em2 = Em1 = Ec2 + Ep2 = 48.804 J
c) Ep3 = 0
Cálculo de v:
Ec3 + Ep3 = Ec1 + Ep1
1/2mv32 +mgh3 = mgh1
v=
2 g ( h1 
h3 ) =
2.9,8.60 m/s =
1176m/s = 34,29 m/s
Ec3 = 1/2mv2 = 1/2. 83Kg. 1176m2/s2 = 48804 J = Ep1
Em3 = Ec3 = 48804J
7
Energía térmica
Mecanismos de transmisión de calor: conducción, convección y radiación. Calor absorbido por un
cuerpo.
CONDUCCIÓN
Se da en los sólidos.
Se llama conducción calorífica al mecanismo de transmisión de energía interna de un cuerpo a otro o
entre una parte de un cuerpo y otra mediante el intercambio de energía cinética de las moléculas por
comunicación directa o en los metales por emigración de los electrones libres.
No hay desplazamiento de materia.
Tiene lugar en los límites del cuerpo o en la línea divisoria entre dos cuerpos que están en contacto.
Por ejemplo, al calentar una barra por un extremo al cabo de un tiempo se calienta el otro extremo que
estaba frío.
La velocidad de conducción de calor a través de un cuerpo por unidad de sección transversal es
proporcional al gradiente de temperatura que existe en el cuerpo.
El factor de proporcionalidad se denomina conductividad térmica del material.
Los materiales como el oro, la plata o el cobre tienen conductividades térmicas elevadas y conducen bien
el calor, mientras que materiales como el vidrio o la cerámica tienen conductividades cientos e incluso
miles de veces menores; conducen muy mal el calor, y se conocen como aislantes.
CONVECCIÓN
Llamamos conducción calorífica al mecanismo de transmisión de calor que tiene lugar en un fluido
cuando una parte de éste se mezcla con otra, debido a los movimientos de masa del mismo.
Clasificación según el
origen del movimiento
del fluido
CONVECCIÓN FORZADA si es debido a
causas mecánicas externas
CONVECCIÓN LIBRE si es debido a
diferencias de densidad creadas por diferencia
de temperaturas en la masa del fluido
RADIACIÓN:
La radiación presenta una diferencia fundamental respecto a la conducción y la convección: las sustancias
que intercambian calor no tienen que estar en contacto, sino que pueden estar separadas por un vacío.
El calor se transmite en forma de ondas electromagnéticas.
El poder emisor de una superficie es proporcional a la cuarta potencia de su temperatura absoluta.
8
El factor de proporcionalidad se denomina constante de Stefan-Boltzmann en honor a dos físicos
austriacos, Joseph Stefan y Ludwig Boltzmann que, en 1879 y 1884 respectivamente, descubrieron esta
proporcionalidad entre el poder emisor y la temperatura. Según la ley de Planck, todas las sustancias
emiten energía radiante sólo por tener una temperatura superior al cero absoluto. Cuanto mayor es la
temperatura, mayor es la cantidad de energía emitida. Además de emitir radiación, todas las sustancias
son capaces de absorberla. Por eso, aunque un cubito de hielo emite energía radiante de forma continua,
se funde si se ilumina con una lámpara incandescente porque absorbe una cantidad de calor mayor de la
que emite.
Calor absorbido por un cuerpo :
Caloría: calor necesario para elevar 1ºC la temperatura (de 14,5ºC a 15,5ºC) de 1 gramo de agua a
presión normal (nivel del mar).
El calor absorbido por un cuerpo de masa m y calor específico ce al aumentar su temperatura es:
Q = ce.m (Tf - Ti)
Donde:
Calor absorbido: [Q] = Kcal
Calor específico: [ce] = Kcal/KgºC
Masa:
[m] = Kg
Temp final:
[Tf] = ºC
Temp inicial:
[Ti ] = ºC
Calor específico: calor que se debe suministrar a 1 Kg de una sustancia para elevar 1ºC su temperatura.
Luego el calor específico del agua ce = 1 Kcal/KgºC.
1 cal = 4,18 J
Ejercicio 1
Dado un depósito que contiene 864litros de agua a 18ºC, calcula la energía en Kcal, en KJ y en KWh
necesaria para calentar el agua hasta 28ºC .
m = ρ.V = 1 Kg/dm3. 864dm3 = 864 Kg
Q = ce.m (Tf - Ti) = 1 Kcal/KgºC . 864 Kg . (28 - 18 ) ºC = 8640 Kcal
E = 8640 Kcal. 4,18 KJ/ Kcal = 36115,2 KJ = 36115,2KWs. 1h/3600s = 10,032 KWh
Ejercicio 2
Calcula la temperatura final de un recipiente de 5l de agua que ha absorbido 300Kcal si se encontraba
inicialmente a 22ºC.
m = ρ.V = 1 Kg/dm3. 5dm3 = 5 Kg
Q = ce.m (Tf - Ti)
Tf = Ti + Q / ce.m
Tf = 22ºC +
300Kcal
= 22ºC + 60ºC = 82ºC
Kcal
1
.5 Kg
Kg º C
9
Energía eléctrica
Se denomina energía eléctrica a la forma de energía que resulta de la existencia de una diferencia de
potencial entre dos puntos, lo que permite establecer una corriente eléctrica entre ambos cuando se los
pone en contacto por medio de un conductor eléctrico.
E = P.t = VI t = I2. R.t
P = VI
V = IR
Donde:
P = potencia
I = intensidad de corriente
R = resistencia
t = tiempo
Unidades:
[P ] = W (watio)
[I ] = A (amperio)
[R ] = Ω (ohmio)
[t ] = s (segundo)
KWh : cantidad de energía transferida por un cuerpo o sistema de potencia 1KW durante 1 h.
1KWh =1000Wh
Ejercicio 1
Un frigorífico está funcionando una media de 12 horas al día. La tensión de red se sabe que es de 220V y
la corriente que lo recorre es de 4 A . ¿Qué energía consume al día en julios y en KWh?
E (J) = P.t = V.I.t = 220 V. 4 A . 12 h . 3600s/1h = 38.016.000 J = 3,8. 107 J
E (KWh) = P.t = V.I.t = 220 V. 4 A . 12 h = 10560 W.h = 10,56 K W.h
Ejercicio 2
Si una plancha de potencia 2000W ha estado en funcionamiento 1,5h, calcula la energía consumida en KJ
y el calor desprendido por la misma en Kcal.
E = P.t = 2KW.1,5h = 3KWh.3600s/1h = 10800 KW.s = 10800 KJ
Q = 10800 KJ. 1 Kcal/ 4,18 KJ = 2583,73 Kcal
Ejercicio 3
Si en una vivienda se han consumido 854KWh , calcula los KJ consumidos, Kcal necesarias en la central
térmica para proporcionar esa energía y la potencia necesaria de la central en KW y en CV funcionando
durante 80h.
E = 854KWh . 3600s/1h = 3074400 KJ (nunca se expresa en KJ la energía de la factura de la luz )
Q = 3074400 KJ . 1Kcal / 4,18 KJ = 735502,39 Kcal (se podría calcular la masa de combustible necesario
quemar en la central para obtener este calor conociendo el poder calorífico del combustible )
P = E/t = 854 KWh / 80h = 10,675 KW
P = 10,675KW . 1CV / 0,735 KW =
14,5CV
10
Energía química de combustión
La combustión es una reacción química exotérmica en la que un elemento combustible se combina con
otro comburente (O2 gaseoso), desprendiendo calor y produciendo un óxido.
Los combustibles son los materiales orgánicos que contienen carbono e hidrógeno. El producto de esas
reacciones puede incluir monóxido de carbono (CO), dióxido de carbono (CO2), agua (H2O) y cenizas.
Para iniciar la combustión de cualquier combustible, es necesario alcanzar una temperatura mínima,
llamada ignición.
Se entiende por poder calorífico de un combustible, la cantidad de calor producida por la combustión
completa de un kilogramo de esa sustancia, en el caso de combustible sólido o líquido y de un m3 en el
caso de un gas.
Líquidos y sólidos:
Pc (Kcal/Kg), luego el calor expresado en Kcal desprendido será:
Q Líquidos y sólidos = Pc.m, donde m: masa en Kg
Gases:
Pc(Kcal/m3), luego el calor expresado en Kcal desprendido será:
Q Gases = Pc.V, donde V: volumen en m3, siempre que el gas se encuentre en
condiciones normales ( 1 atm y 0ºC).
Si el gas se encuentra en otras condiciones, utilizamos la ecuación de los gases
perfectos y calculamos V en condiciones normales, V1:
P.V /T = cte
P.V/T = P1.V1/T1 donde : V1, P1, T1 en condiciones normales y V, P, T en
otras condiciones.
Cálculo de V1 :
V1 = P/P1.T1/T.V
Sustituyendo para P1 = 1 atm, T1 = 273 K y T =273 + t
V1 = P/1atm . (273/273+t).V
Qgases = Pc. P/1atm (273/273+t)V
Ejercicio 1:
Calcula el calor liberado por la combustión de 100g de carbón vegetal, sabiendo que su poder calorífico
es de 7300Kcal/Kg.
Q = Pc carb.vege. mcv = 7300 Kcal/Kg. 0,1 Kg = 730 Kcal
Ejercicio 2:
Calcula el calor generado en Kcal en la combustión de 1,5m3 de propano a una presión de 1,2 atm y a una
temperatura de 25ºC si su poder calorífico es de 22.350 Kcal/m3.
Q = Pc. P/1atm (273/273+t)V = 22.350 Kcal /m3. 1,2 atm/1atm (273/273+25).1,5m3 = 36.855 Kcal
11
Ejercicio 3:
Se necesita generar una energía de 100 KW.h mediante un generador que utiliza un combustible gaseoso
de 30.000 Kcal/m3 de poder calorífico a una presión de 2atm y a una temperatura de 26ºC. Se pide
calcular el volumen de gas necesario.
Q = 100KW.h.3600s/1h = 360.000 KW.s = = 360.000 KJ = 360.000 KJ .1Kcal/4,18KJ = 86.124,4 Kcal
Qgases = Pc. P/1atm (273/273+T)V
V=
Qgases
P
273
Pc.
.
1atm 273  28
=
86.124,4 Kcal
= 1,572m3
Kcal 2atm 273
30.000 3 .
.
m 1atm 299
Energía nuclear de fisión
Se llama energía nuclear de fisión a aquella que se obtiene al aprovechar las reacciones nucleares
espontáneas o provocadas por el ser humano. Estas reacciones se dan en algunos isótopos de ciertos
elementos químicos, siendo el más conocido de este tipo de energía la fisión del uranio-235 (U235), con la
que funcionan los reactores nucleares. Sin embargo, para producir este tipo de energía aprovechando
reacciones nucleares pueden ser utilizados muchos otros isótopos de varios elementos químicos, como el
torio, el plutonio, el estroncio o el polonio.
E = m.c2
Donde:
E = energía
m = masa de combustible
c = velocidad de la luz (3.108m/s)
Unidades:
[E ] = J (julio)
[m ] = Kg (Kilogramo)
[c ] = m/s
Ejercicio:
Si en una reacción nuclear de fisión se utilizan 3g de uranio , calcula la energía en julios y en Kcal
liberada suponiendo despreciables las pérdidas.
E = m.c2 = 3.10-3 Kg.(3.108)2 m2/s2 = 33.1013J = 2,7.1014J.1cal/4,18J = 6,46.1013cal = 6,46.1010Kcal
12
Rendimiento:
Relación entre el trabajo o energía útil realizado por una máquina y la energía que ha sido necesario
suministrarle.

Eútil
Esu min strada  Eperdida
Eperdida

1
1
Esu min strada
Esu min strada
Esu min strada
Se suele expresar en % y es adimensional, puesto que es una relación entre magnitudes homogéneas.
Como el trabajo útil y la energía suministrada se desarrollan en el mismo tiempo, también el rendimiento
se puede expresar como relación entre potencia útil y potencia suministrada.
Esuministrada
Eútil
Eperdida
Las máquinas no transforman toda la energía que se les suministra en energía útil, sino que parte de la
energía se pierde en forma de calor, rozamiento, etc y no se puede aprovechar.
Por ejemplo, un motor de explosión ronda el 25% de rendimiento, las placas solares fotovoltaicas un
15%, un radiador eléctrico 90%.
NOTA:
El trabajo o energía útil desarrollado por una máquina se emplea en variar la energía mecánica de un
cuerpo o sistema:
Wútil = Eútil = ∆Em
Wútil = Em2-Em1 = (Ec2+Ep2) - (Ec1+Ep1) = (Ec2 – Ec1 ) + (Ep2 – Ep1 ) = ∆Ec + ∆Ep
Luego el trabajo útil desarrollado por una máquina se emplea en variar la energía cinética y la energía
potencial de un cuerpo o sistema.
13
Ejercicios de selectividad:
Cuestión nº2
Un ascensor cuya masa es de 800 Kg sube desde el nivel de calle hasta un piso situado a
30m de altura. Suponiendo despreciables las pérdidas, se pide calcular:
a) Variación de la energía potencial del ascensor.
b) Trabajo que debe realizar el motor del ascensor.
c) Potencia necesaria del motor del ascensor si debe realizar el recorrido en 25s.
OPCIÓN BSeptiembre 98_99
a)
b)
c)
∆Ep = Ep2-Ep1 = mg (h2-h1) = 800Kg. 9,8m/s2 . (30m – 0m) = 235.200 J
Wascensor = ∆Ep = 235.200 J
P = E/t = 235.200J/ 25s = 9408W = 12,8 CV
OPCIÓN A Septiembre 2002_03
a) Wu = ∆Ep =mgh = 2500Kg. 9,8m/s2 .21m = 514.500 J
b) Pabsorbida = 220V.35A = 7.700W
c) P util = Eu/t = Wu/t = 514500 J/180s =2.858,33 W
d) η = P util/ Pabsorbida =2.858,33 W/7.700 W = 0,37 = 37%
Junio 2004_05
14
2
1
1
 120.10 3 m 
a) Wu  Ecin  mv 2  1100 Kg
  611.111J  6,1.10 5 J
2
2
 3600s 
b)
Wu 6,1.105 J

 4,7.104 W  47KW  64CV (1CV =735 W)
Putil =
t
13s
c)
η=
Putil
= 0,21
Psum
Putil
 224KW
0,21
Es = mc.Pc
Es = Ps.t =224KJ/s.13s = 2910KJ
Psum 
d)
mc = Es/Pc = 2910 KJ/41.800KJ/Kg = 0,070Kg = 70 g
Sep 2005
2
2
3
3
a) Wu  Ecin  1 mv 2  v 2   1 1150 Kg  130.10 m    75.10 m    500.321J  5.10 5 J
2
1
2
b)
η=
2
 3600s 
 3600s  
Eutil
= 0,225
Esum
Etotal = Eutil/ η = 5.105J/0,225 = 2.223.649 J
c)
Et = Qcombustión = mc.Pc
mc= Et/Pc = 2.223.649 J/4.104 J/g = 55,6g
d)
Pu = Eu /t = 5.105J/7s = 71.428 W (= 97CV)
P = M.w
M = P/w=
71.4284 W
 166,36N .m
4100.2. / 60s  1
15
OPCIÓN B Septiembre 2002_03
a) Wutil = ∆Ep + ∆Ec =mgh + 1/2mv2 = 1600 Kg.9,8m/s212m+ 1/21600Kg.22m2/s2
=191360 J
b) Pu = Eu/t = Wu/t = 191360 J/16s = 11.960W
c) Pabs = Pu/ η =11.960 W/0,61 =19.606,6 W
Junio 2005_06
2
a)
1 2 1
 105 m 
Ecin  mv  1220 Kg
  470679 J
2
2
 3600s 
b) Elib = m.Pc = 550g. 45500 J/g = 25025000J
c) η =
d)
Wutil
470679
=
*100 = 1,88 % ?????
Wlib 250250000
Putil = Eutil/t
4,7.105 J
 4,7.104 W  47KW  64CV (1CV =735 W)
Putil =
10s
P = M.w
M = P/w=
4,7.104 W
 112,2 N .m
4000.2. / 60s  1
16