MOVIMIENTO EN DOS DIMENSIONES

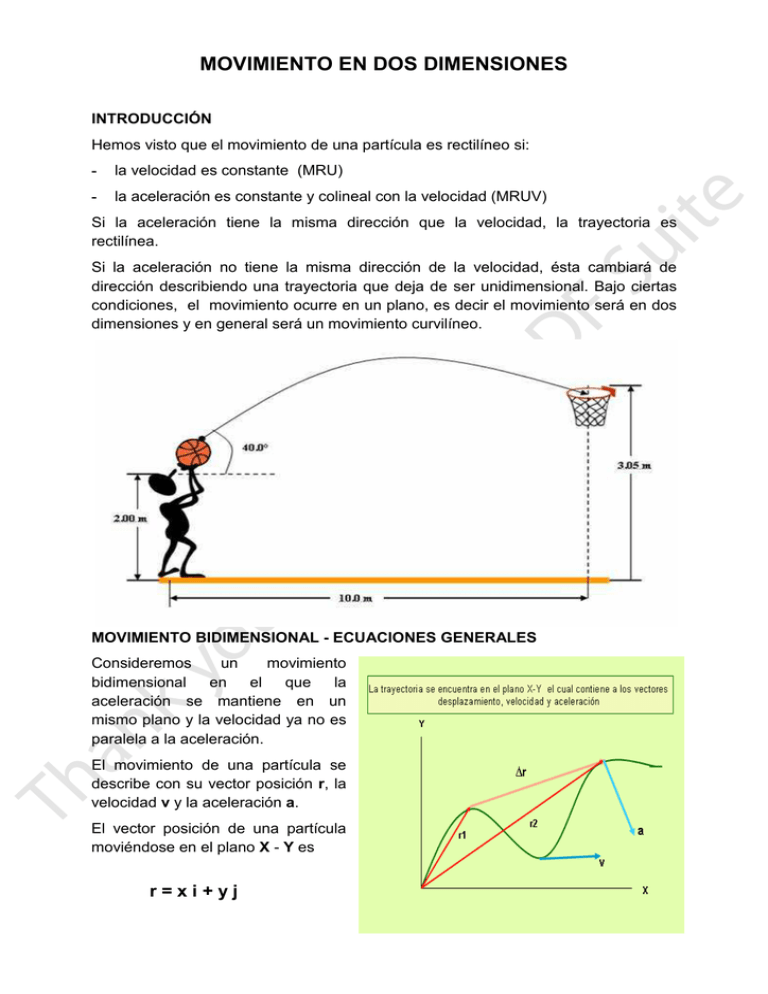
MOVIMIENTO EN DOS DIMENSIONES
INTRODUCCIÓN
Hemos visto que el movimiento de una partícula es rectilíneo si:
-
la velocidad es constante (MRU)
-
la aceleración es constante y colineal con la velocidad (MRUV)
Si la aceleración tiene la misma dirección que la velocidad, la trayectoria es
rectilínea.
Si la aceleración no tiene la misma dirección de la velocidad, ésta cambiará de
dirección describiendo una trayectoria que deja de ser unidimensional. Bajo ciertas
condiciones, el movimiento ocurre en un plano, es decir el movimiento será en dos
dimensiones y en general será un movimiento curvilíneo.
MOVIMIENTO BIDIMENSIONAL - ECUACIONES GENERALES
Consideremos
un
movimiento
bidimensional en el que
la
aceleración se mantiene en un
mismo plano y la velocidad ya no es
paralela a la aceleración.
El movimiento de una partícula se
describe con su vector posición r, la
velocidad v y la aceleración a.
El vector posición de una partícula
moviéndose en el plano X - Y es
r=xi+yj
Si se conoce el vector posición la velocidad de la partícula se puede obtener como
v = vx i + vy j
En las ecuaciones x, y, vx , y vy , componentes de r y v, varían con el tiempo
cuando se mueve la partícula.
La aceleración de la partícula en el plano estará definida por las componentes
a = ax i + a y j
Si el movimiento es con aceleración constante, entonces ax y ay, componentes de
la aceleración serán constantes y estarán en un mismo plano.
Si la partícula inicia su movimiento con velocidad inicial v0, esta es
v0 = vx0 i + vy0 j
Aplicando las ecuaciones cinemáticas a las componentes de la velocidad v para
cualquier instante t con aceleración constante:
vx = vx0 + ax t
vy = vy0 + ay t
Reemplazando estas expresiones en la ecuación de la velocidad v = v0 + a t
v = (vx0 + ax t ) i + (vy0 + ay t) j
Lo que significa que la velocidad de una partícula en un instante t es igual a la suma
del vector velocidad inicial v0 y la velocidad adicional, at, que adquiere en el tiempo t
De la misma forma remplazando en , r = r0 + v0 t + ½ a t2 , las posiciones o
coordenadas x, y de una partícula que se mueve con aceleración constante con sus
componentes
x = x0 + vx0 t + ½ a x t2
y = y0 + vy0 t + ½ a y t2
r = (x0 + vx0 t + ½ a x t2 ) i + (y0 + vy0 t + ½ a y t2 ) j
r = (x0 i + y0 j) + (vx0 i + vy0 j) t + ½ (a x i + ay j) t2
MOVIMIENTO EN DOS DIMENSIONES CON ACELERACIÓN CONSTANTE
El movimiento de una pelota pateada
por un futbolista, el de una piedra que
gira atada a una cuerda o el movimiento
de la luna alrededor de la tierra, son
ejemplos de movimiento en el plano.
En el caso de un movimiento en el cual la aceleración es constante y no colineal con
v, la trayectoria seguida por la partícula es una parábola. La parábola esta en plano
formado por la aceleración y la velocidad. El vértice se encuentra en la posición en
que la velocidad y la aceleración son perpendiculares entre si
La velocidad inicial v0 y la aceleración a
determinan el plano del movimiento de la
partícula
La aceleración a = ax i + ay j
tiene
componentes ax constante y ay, constante
La aceleración siempre apunta hacia la parte
cóncava de la curva
El eje de la parábola es paralelo a la
aceleración
Las ecuaciones de la posición de
la partícula serán
x = x0 + vx0 t + ½ a x t2
y = y0 + vy0 t + ½ a y t2
Las ecuaciones de la velocidad
de la partícula serán
vx = vx0 + ax t
vy = vy0 + ay t
v2x = vx0 + 2 ax ∆ X
v2y = vy0 + 2 ay ∆ X
Estas ecuaciones indican que las proyecciones sobre los ejes coordenados X e Y se
mueven con MRUV y ambas ecuaciones están relacionadas por un parámetro
común que es el tiempo
Si una de los ejes coordenados es paralelo a la aceleración de la partícula el otro eje
no tendrá componente de la aceleración y el movimiento en ese eje será MRU
MOVIMIENTO DE PROYECTILES
En este movimiento la aceleración a es
la que produce la tierra sobre todos los
cuerpos, la aceleración de la gravedad g,
en dirección vertical y con sentido hacia
el centro de la tierra. La representamos
vectorialmente como g = 9,81 (-j ) m/s2.
Para simplificar los cálculos aproximamos
su valor a 10 m/s2.
Al lanzar el proyectil desde la superficie
terrestre, o cerca de ésta, con una velocidad
inicial que hace un ángulo θ con la horizontal,
el proyectil sigue una trayectoria parabólica en
el plano determinado por su velocidad inicial v0
y la gravedad g como se aprecia en la figura
El vector posición r en cada punto de la trayectoria parabólica se representa en el
siguiente gráfico. Observe que si no existiera aceleración g el recorrido del móvil
sería rectilíneo en la dirección de v0t, el vector ½gt es el desplazamiento vertical
debido a la aceleración g dirigida hacia abajo.
Y
MRUV
MRU
MRU
En la figura la expresión vectorial para r es:
X
r = v0t + ½gt2
Para deducir las ecuaciones que describen el movimiento, establecemos un sistema
de coordenadas. La aceleración g actúa verticalmente, por tanto, sólo afecta a la
componente vy, mientras que vx permanecerá constante e igual a v0x como se
aprecia en esta figura
Podemos concluir entonces que el movimiento de proyectiles es la superposición de
dos movimientos: a) movimiento a velocidad constante en la dirección inicial y b) el
movimiento de una partícula que cae libremente en la dirección vertical con
aceleración constante
Las componentes del vector velocidad son vx y vy para varios puntos de la
trayectoria. La componente vx se mantiene constante e igual a vx0. La
componente vy varía debido a la aceleración de gravedad g de valor
constante. Puntos simétricos de la trayectoria tienen la misma rapidez.
.Deduciremos entonces:
- x, el desplazamiento horizontal y vx, la componente de la velocidad en el eje X
-
y, el desplazamiento vertical y vy, la componente de la velocidad en el eje Y
Aplicaremos las ecuaciones cinemáticas para el movimiento en cada eje:
a) En el eje X el movimiento es uniforme como el MRU
b) En el eje Y el movimiento tiene aceleración constante, emplearemos la
ecuación del MRUV
Ecuaciones para el movimiento parabólico
En cada punto de la trayectoria del proyectil el vector posición r, la velocidad v y la
aceleración g del proyectil se expresan en función de sus componentes como:
r =xi+yj
v = vx i + vy j
g = −gj
Velocidad inicial
v0x =
v0 = v0x i + v0y j.
v0 Cos θ
v0y = v0
Sen θ
Posición
En el caso general el origen del sistema de coordenadas no corresponde a la
posición inicial, es decir: r0 = x0 i + y0 j.
La posición de la partícula
r =xi+yj
En el eje X
x = x0 + vx0 t
vx = vx0
( MRU)
x = x0 + (v0 cos θ0 )t
En el eje Y, la aceleración es constante en el sentido negativo del eje Y, por tanto el
movimiento es descrito por las ecuaciones del MRUV.
y = y0 + vy0 t – (½)gt 2
(MRUV)
y = y0 +v0 sen θ0 t – (½)g t 2
Velocidad
El vector velocidad es el movimiento en plano esta definido por v = vx i + vy j
La velocidad en el eje X
vx = v0 cos θ0
vx2 = v0x2 –2g(∆X)
La velocidad en el eje Y
vy = vy0 – gt
vy = v0 sen θ0 t – g t
vy2 = vy02 –2g(∆y)
Por tanto el vector posición r del proyectil en cualquier instante t es:
r = ( x0 + (v0xt ) i + ( y0 +v0y t – (½)gt 2 ) j
y la velocidad v del proyectil en un instante t es:
v = (v0x) i + (v0y t – gt) j
Ecuación de la parábola
x
y remplazamos en la
voCosθ
ecuación de y obteniendo la ecuación de la trayectoria de la partícula.
De la ecuación de
t=
x deducimos el tiempo
y = voSen(
x
1
x
+ g(
)2
voCosθ ) 2 voCosθ
Altura Máxima (Hmax)
Un proyectil lanzado con un ángulo de elevación, va ganando altura hasta llegar al
punto más alto de su trayectoria que corresponde a la altura máxima. Observar que
la aceleración de la gravedad g actúa solo sobre la componente vertical de la
velocidad inicial, vy0, mientras que vx0 permanece constante. Deduciremos la
expresión para la altura máxima si se conoce v0 y θ0, el punto de lanzamiento se
considera el origen del sistema de coordenadas (x0 = 0 y0 = 0).
En el punto más alto la componente vertical de la velocidad vy = 0, entonces según
la ecuación
0 = vy0 t – gt
voSenθ
g
ts =
esto indica que para
donde ts es el tiempo de subida del proyectil.
Se alcanza la altura máxima, reemplazando ts y y0 = 0
2
Hmax = y = vy0 t – (½)gt =
simplificando
v yo ( v yo )
g
2
−
(1/2)g(v yo )
2
g
vo 2
h max =
Sen 2θ o
2g
el vector posición cuando el proyectil alcanza la altura máxima es:
r = ( R/2 ) i + Hmax j
Si fuera posible variar el ángulo de lanzamiento, manteniendo constante la rapidez,
deducimos que para θ0 = 90˚ el proyectil
llega a lo más alto que puede alcanzar. En
la figura se ilustra que el proyectil alcanza
diferentes alturas máximas para diferentes
ángulos de lanzamiento, con v0 fijo.
En la figura se observa la máxima altura
para diferentes ángulos de lanzamiento,
Alcance (R)
Cuando el proyectil vuelve a su altura inicial (y = y0), se habrá desplazado
horizontalmente una distancia que se denomina alcance denotado por R (también se
le conoce como rango). Para determinar R recordemos que el movimiento es MRU a
lo largo del eje X.
R = vx0 tv
Donde tv es el tiempo que le toma al proyectil volver a la altura inicial, o tiempo de
vuelo (tv = 2 ts). Si el proyectil se lanza desde el origen del sistema de coordenadas,
y0 = 0. En la ecuación
y = vy0 t – (½)gt 2
Si hacemos x= 0 , y = 0, obteniendo tv = (2 vy0)/g, reemplazando tv resulta
v02 sen 2θ0
2 vx0 v0y
R=
=
g
g
Dos proyectiles disparados con ángulos complementarios tienen el mismo alcance
Se puede notar de esta expresión que para θ0 = 45º el proyectil cubre el máximo
alcance.
vo 2
g
Si se apunta directamente a un blanco que cae a partir del reposo, el proyectil
necesariamente al blanco, siempre que el rango sea mayor a Rango/2
R max =
Ejemplo 1
Si desde la tierra se lanza un proyectil con una velocidad inicial de 50 m/s formando
un ángulo de 37º respecto a la horizontal. a) ¿A qué altura en metros se encuentra el
∧
∧
proyectil cuando su velocidad sea de 40 i − 20 j . b) Calcule además la altura máxima.
Solución
a)
y = Voyt – gt2/2
y = (Vo Cos37º) t – gt2/2 ..............(*)
Falta conocer t.
Pero la ecuación
→
∧
∧
V = 40 i − 20 j
Se tiene:
Vy = Voy – gt
– 20 = VoCos37º – 10t
– 20 = 50 (5/4) – 10t
donde:
t = 5s.
Reemplazando en (*)
y = h = 50(4/5)(5) – g/2(5)2 = 25m
b)
hmax =
2
Voy
2g
=
30 2
= 45m
20
Ejemplo 2 Un proyectil es lanzado con v0= 3,6 m/s y θ0 = 78, 7˚, determine la
ecuación de la trayectoria.
Con estos datos de la ecuación anterior resulta
10
x2 = 5x – 5x2
y = (tan 78, 7˚)x –
2 (3,6)2 cos2 (78, 7˚)
completando cuadrados se obtiene
y – 5/4 = – 5(x - ½) 2
que es la ecuación de una parábola con vértice en (h, k) = (1/2, 5/4) y c = -5. La
siguiente figura representa esta parábola que viene a ser la trayectoria de una
partícula lanzada con una rapidez de 3,6 m/s y un ángulo de elevación de 78,7˚.
Ejemplo 3
Se lanza una partícula desde el origen de un sistema de coordenadas con una
∧
∧
velocidad de v = (2 i + j ) m / s . Si la aceleración es a = +10
m∧
j determine la ecuación
s2
de la trayectoria.
Solución
→
r =r•t+
a 2
t ;
2
de donde:
Despejando t de la primera ecuación t =
y = (Tanθ o )x +
y=
5
Vox
2
1
1
x+
x2
2
2
 2 




 5
x2
 t2 
y = Voy t + 10 
2
x = Vox t
x
y reemplazando en la segunda.
Vox
y = Tanθ o x +
5
Vo2 Cos 2 θ o
Ec. de la trayectoria
x2
y=
y=
1
5
x+
x2
2
5Cos 2 θ o
1
5
x + x2
2
4
.