Atmosfera isotermica vs adiabática

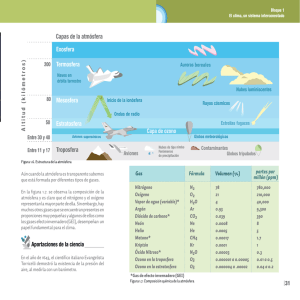
Aguerreberry, Emiliano. Virgillito,
Física II (B y G) – Práctica Especial –
Marisol.
Trabajo Práctico Especial
Objetivo
Comparar la distribución de probabilidad en una atmósfera isotérmica y en una
atmósfera adiabática, centrando el estudio en la capa baja de la atmósfera, la
Troposfera. Averiguar la difusión de las partículas en ambas atmósferas en función de
la altura.
Introducción
La Atmósfera Terrestre
Es la capa gaseosa que rodea al planeta tierra y está unida a él por la fuerza de
gravedad, por ello la acompaña en sus movimientos de rotación y traslación. Esta
formada por una mezcla de gases que varía con la altura. Básicamente, esta
compuesta por nitrógeno (78%), oxígeno (21%), anhídrido carbónico y gases raros
(cerca del 1%), vapor de agua y partículas sólidas en suspensión.
Alguno de ellos, sin embargo juega un rol fundamental en el resguardo de la vida en la
tierra, por ejemplo el ozono (O3), protegiéndola de la radiación ultravioleta.
La atmósfera regula la temperatura de la tierra, atemperando las variaciones térmicas
entre el día y la noche. En la luna, donde no hay atmósfera la temperatura media de la
superficie durante el día es de unos 110ºC y durante la noche de –150ºC.
Conforme aumenta la altura la densidad de la atmósfera disminuye con gran rapidez.
Dentro de los 5,5 kilómetros más cercanos a la superficie se encuentra la mitad de la
masa total y antes de los 15 kilómetros de altura está el 95% de toda la materia
atmosférica. Por otro lado, a medida que nos alejamos de la superficie terrestre
disminuye la presión y la temperatura.
Para su estudio resulta útil dividir la atmósfera en capas en las que el gradiente
térmico es aproximadamente constante y en las que predominan diferentes procesos.
Ellas son, desde la superficie hacia el espacio exterior: la troposfera, tropopausa,
estratosfera, estratopausa, mesosfera, mesopausa e ionosfera.
Figura 1: Distintas capas concéntricas de la atmósfera alrededor de la tierra.
1
Aguerreberry, Emiliano. Virgillito,
Física II (B y G) – Práctica Especial –
Marisol.
La Troposfera
Es la capa que está en íntimo contacto con la superficie terrestre y es uno de los
componentes más importantes del clima terrestre. Es el presupuesto energético de la
troposfera, la que primordialmente determina el estado del clima global, por ello es
esencial comprender su composición y estructura.
La vida, las nubes, los vientos, el vuelo de los aviones, etc. se desarrollan en esta
capa. Su espesor no es constante en toda la Tierra, sino que en los polos tiene casi la
mitad de espesor que en los trópicos. Tiene un grosor que varía desde 8 Km en los
polos hasta 16 Km en el ecuador.
En la troposfera, la temperatura va decreciendo en forma constante con la altura
(
= - 6.5 ºC/Km) hasta llegar a una temperatura de unos –56°C, en donde se
estabiliza en una zona de transición conocida como la tropopausa.
Figura 2: Variación esquemática de la temperatura de la atmósfera terrestre con la altura. Las regiones en que el
gradiente de temperatura es constante determinan las distintas capas de la atmósfera.
Una observación atenta de la temperatura de la atmósfera en función de la altura,
revela que existen regiones en las que las que el gradiente térmico
( Γ=dT/dz=”Temperature lapse rate”) es aproximadamente constante y regiones de
transición donde el gradiente térmico tiene cambios significativos pero donde la
temperatura misma es aproximadamente constante.
2
Aguerreberry, Emiliano. Virgillito,
Física II (B y G) – Práctica Especial –
Marisol.
Fundamento y modelos conceptuales
Distribución
Para analizar y poder explicar la distribución (densidad) de la troposfera tenemos que
considerar dos modelos distintos, el modelo isotérmico y el adiabático.
Atmósfera Isotérmica
Podemos pensar en la idea de que la atmósfera es un gas que intercambia
constantemente calor con el medio que lo rodea, para el caso particular de la
troposfera lo hará con la tierra y con la estratosfera, por lo tanto, el modelo más simple
de la atmósfera es suponer que es isotérmica, es decir, suponemos que
Tº=Tºpromedio =cte. (temperatura promedio en la troposfera es = 288K)(*) en toda la
troposfera.
A su vez, suponemos que esta se comporta como un gas ideal y que la fuerza
gravitatoria es independiente de la altura. De modo que si pensamos en el movimiento
de una partícula, su energía potencial es:
(1)
Y podemos describir su movimiento con la Ley de Boltzmann donde nos dice que la
probabilidad de encontrar a la partícula a una altura h es:
(- h/ho)
(2)
donde
(3)
[k]= 1.3806503 × 10−23 J/k cte. de Boltzmann
[T]=, Tº=Tºprom = 288 K
[m]=4.65x10-23 masa molar promedio de una partícula de aire
[g]= 9.8 m/seg2 determinada altura.
Y según la ley de gases ideales:
(4)
Con
;
(5)
(6)
[M]=kg
[n]=mol
[Mmol]=kg/mol
3
Aguerreberry, Emiliano. Virgillito,
Física II (B y G) – Práctica Especial –
Marisol.
Según la ecuación:
(7)
[h]=altura
=9.8 m/s2
podemos volver a re escribirla como:
(8)
Haciendo una serie de cálculos, integrando las variables y reemplazando éstas en la
ecuación de Boltzmann podemos obtener una fórmula para la presión y otra para la
densidad y son las siguientes:
(9)
[ho]= 8.5 km
(10)
Atmósfera adiabática
Por otro lado, en la Troposfera, cuando las masas de aire que poseen distinta
temperatura ascienden o descienden, en general lo hacen suficientemente rápido de
modo que intercambian poca energía con su medio y además, sabemos que el aire es
un mal conductor del calor. Por consiguiente, es razonable suponer que los
movimientos de las masas de aires son adiabáticos, por ende dentro de esta capa
atmosférica la temperatura no será constante y podremos encontrar un gradiente de
temperatura que variará con la altura (h).
En este caso entonces, para encontrar la distribución de partículas tendrá otro tipo de
ajuste debido a que tal temperatura no es constante y que la presión no se puede
describir únicamente con la ecuación de gas ideal.
= 1.4
(11)
[Cp]=7/2 R
[Cv]=5/2 R
Luego
(12)
Haciendo una serie de reemplazos y combinaciones matemáticas, obtenemos la
temperatura para una atmosfera adiabática
4
Aguerreberry, Emiliano. Virgillito,
Física II (B y G) – Práctica Especial –
Marisol.
(13)
Volviendo a utilizar la ecuación (7) e integrando nuevamente, obtenemos la ecuación
de presión en función de la altura:
(14)
Remplazando las ecuaciones T(h) y P(h) en la ecuación (8) obtenemos:
(15)
Que es la ecuación de distribución para una atmosfera adiabática.
Difusión
En la segunda parte del trabajo quisimos averiguar como seria la difusión de partículas
para los dos modelos de atmosféricos.
Como en la atmosfera isotérmica la temperatura es constante, utilizamos las
herramientas vistas en la práctica de Random Walks para describir el movimiento de
estas partículas.
Sabemos que:
Pup + Pdown =1
donde P(1)*P(1
2)= P(2)*P(2
(16)
1)
(17)
(18)
Luego,
(19)
Para el caso de la atmosfera adiabática la probabilidad dependerá de la altura y de la
temperatura e ira variando en cada paso.
5
Aguerreberry, Emiliano. Virgillito,
Física II (B y G) – Práctica Especial –
Marisol.
Utilizando la ecuación (15) de distribución en función de la altura y calculando las
probabilidades de la misma manera que para el caso isotérmico, obtenemos la ecuación
de probabilidad para el caso adiabático:
1/
(20)
Resultados experimentales
Distribución
En primera instancia comparamos las presiones y temperaturas para ambos modelos,
como así también las dos formas de distribución.
Gráfico1: Comparación de la presión isotérmica (azul) y presión adiabática (roja) en función de la altura.
Tanto la presión isotérmica como la presión adiabática están directamente
relacionadas con la densidad atmosférica, disminuyendo ambas conforme aumenta la
altura. La presión adiabática es menor debido a que esta a su vez esta influenciada
por el gradiente térmico que disminuye a medida que aumenta la altura.
6
Aguerreberry, Emiliano. Virgillito,
Física II (B y G) – Práctica Especial –
Marisol.
Gráfico2: Comparación de la densidad isotérmica (azul) y densidad adiabática (rojo) en función de la altura.
En este gráfico observamos que existe una pequeña diferencia en cuanto a la forma
de distribución, y que estas dos se cruzan debido a que la función isotérmica se ajusta
a una función exponencial y su gradiente disminuye linealmente, mientras que el
gradiente adiabático se ajusta a otro tipo de función.
Difusión
Para analizar como seria la difusión en ambos modelos, calculamos como variaría la
probabilidad en función de la altura para luego realizar un Random Walk para una
gran cantidad de partículas y poder acercarnos a sus distribuciones y compararlas.
Gráfico 3a): Comparación de la probabilidad isotérmica (azul) con la probabilidad adiabática (rojo) en función de la
altura. Gráfico 3 b): Probabilidad adiabática en función de la altura.
Vemos que en el caso isotérmico, la probabilidad que tiene una partícula de subir o de
bajar es constante en todo el espesor de la atmosfera ya que la temperatura no varía
en función de la altura.
7
Aguerreberry, Emiliano. Virgillito,
Física II (B y G) – Práctica Especial –
Marisol.
En cambio la probabilidad adiabática es redefinida en cada paso debido a que existe
un gradiente de temperatura y tanto la presión como la densidad se ven afectadas,
disminuyendo a medida que aumenta la altura.
Gráfico 4: A la derecha histograma para la distribución de partículas para el caso isotérmico. A la izquierda, mismo
histograma de partículas para el caso isotérmico y se graficó además las curvas de densidad en función de la altura
para el caso isotérmico (azul) y para el caso adiabático (rojo).
En el gráfico 4 observamos que el histograma para el caso isotérmico se acerca
bastante al modelo de densidad, lo cual nos da una idea de cómo es el tipo de
distribución para una atmosfera isotérmica.
Si bien, al graficar el histograma y las curvas de densidad todo en un mismo gráfico
(gráfico de la derecha), el mismo se nos va de escala, no observando una correlación
en los valores para ambos gráficos.
Suponemos que esto se debe a un error en los valores de las escalas.
Gráfico 5: Histograma para la distribución de partículas para el caso adiabático. Además están graficadas sobre el
mismo gráfico las curvas de densidad en función de la altura para el caso isotérmico (azul) y para el caso adiabático
(rojo).
En este caso, no pudimos encontrar una buena distribución de partículas que se
ajustara bien al modelo de densidad adiabático.
Creemos que es debido a la forma de graficar el histograma y las curvas de densidad
juntas, ya que tuvimos problemas a la hora de ajustar las dos escalas de los gráficos
superpuestos. Y nos falto tiempo y conocimiento del uso de Matlab para realizarlo.
8
Aguerreberry, Emiliano. Virgillito,
Física II (B y G) – Práctica Especial –
Marisol.
Conclusión
Comparando los dos modelos de distribuciones (Isotérmica y Adiabática), observamos
que no hay una diferencia significativa para explicar el tipo de distribución espacial que
existe en la atmosfera y que ambos modelos podrían coexistir. Como se observa en el
gráfico 2 a una altura aproximada a los 15 km.
En cuanto a lo que respecta a la difusión de partículas, observamos que la diferencia
se podría deber al efecto del gradiente térmico. A una temperatura menor, las
partículas tienen una menor energía cinética, su velocidad instantánea es menor, y por
lo tanto se mueven mas lento, tardando mas tiempo en chocar con otras partículas,
aumentando la probabilidad de quedarse a una determinada altura.
Como conclusión de los histogramas realizados, lo que podemos decir es que
tendríamos que volver a graficar las curvas de densidad con el histograma y encontrar
de alguna manera un buen ajuste de los valores para poder comparar bien los
modelos. Aclaramos nuevamente que nos falto tiempo y conocimiento para poder
realizarlo correctamente.
(*)Dato teórico obtenido, según las referencias.
Referencias
http://www.fisicarecreativa.com/papers_sg/papers_sgil/Docencia/Atmosfera_Terrestre.pdf
http://pagesperso-orange.fr/ballonsolaire/es-theorie2.htm
http://www.unne.edu.ar/Web/cyt/cyt/2001/8-Exactas/E-017.pdf
http://es.wikipedia.org/wiki/Difusi%C3%B3n
9