filtrado de fase en el espectro tridimensional

FILTRADO DE FASE EN EL ESPECTRO TRIDIMENSIONAL
DE IMÁGENES EN COLOR
Josep Nicolás1, Ignacio Moreno2, Juan Campos1 y María J. Yzuel1
1
2
Departament de Física, Universitat Autònoma de Barcelona, 08193 Bellaterra.
Dept. Ciencia y Tecnología de Materiales, Univ. Miguel Hernández, 03202 Elche.
Resumen
En este trabajo estudiamos la aplicación del filtro sólo de fase a imágenes multicanales
en color interpretadas como señales tridimensionales, con dos dimensiones espaciales y
una tercera dimensión de color. Esta interpretación permite aplicar la transformada de
Fourier 3D a imágenes en color, y por tanto extender las operaciones de filtrado de
frecuencias al caso 3D. Analizamos las implicaciones colorimétricas de realizar un
blanqueo de frecuencias a lo largo del eje del color, y aplicamos el blanqueo del
espectro 3D al reconocimiento de patrones en color mediante correlación 3D.
1. Introducción
El reconocimiento de patrones en color mediante la operación de correlación multicanal
ha venido empleándose desde hace años [1]. Esta operación consiste en descomponer la
escena y el patrón a detectar en sus respectivas componentes, y realizar la correlación en
cada uno de los canales por separado, para posteriormente combinar la información de
los diversos canales. Se han empleado filtros de frecuencias usuales en el procesado
monocromático con el fin de mejorar las propiedades de la correlación de cara al
reconocimiento. En particular, el filtro sólo de fase proporciona picos de correlación
estrechos y optimiza la eficiencia energética [1]. Por otra parte, la aplicación de la teoría
de la detección a imágenes multicanales ha demostrado que la solución óptima respecto
a la relación señal-ruido en presencia de ruido aditivo gaussiano es la suma de las
amplitudes de la correlación en cada canal [2]. Recientemente hemos propuesto la
interpretación de una imagen multicanal en color como una señal tridimensional, con
dos dimensiones espaciales usuales, siendo la distribución de color en cada píxel la
tercera dimensión [3]. Esta interpretación ha permitido aplicar la transformada de
Fourier 3D y la función de correlación 3D a las imágenes en color. En particular la
suma de las amplitudes de la correlación 2D en cada canal se obtiene en el origen de
color (canal cero) de la correlación 3D. En este trabajo estudiamos la aplicación del
filtro solo de fase al caso de esta señal 3D, y analizamos la transformación colorimétrica
producida por el blanqueo del espectro de color [4].
2. Transformada de Fourier 3D y transformada de Fourier del color
Consideramos una imagen en color como una función de tres coordenadas f(x,y,n),
donde x e y representan las coordenadas espaciales y n=0,1,2...N−1 indica el canal de
color. Típicamente, en imágenes RGB se tiene N=3 y asignamos los índices n=0,1,2 a
los canales rojo, verde y azul respectivamente. La transformada de Fourier
tridimensional F3D(u,v,m) de esta función es
F 3 D (u , v , m ) =
D x −1 D y −1 N −1
∑∑∑
x =0 y = 0 n =0

 ux
vy
mn 
 ,
f (x , y , n )exp − i 2 π
+
+

D
D
N
x
y



(1)
donde u y v son las frecuencias espaciales en direcciones x e y, m es la frecuencia de
color, y Dx y Dy son las dimensiones de la imagen en direcciones x e y. También
podemos definir la transformada de Fourier del color FC(x,y,m) haciendo la
transformada solamente a lo largo del eje del color, es decir,
F C (x , y , m ) =
N −1
∑ f (x , y, n )exp − i 2π mnN  .
(2)
n =0
Si aplicamos esta definición al caso de las imágenes RGB se obtienen las siguientes
expresiones para las componentes de FC(x,y,m):
F C (x , y ,0 ) = R (x , y ) + G (x , y ) + B (x , y ) ,
(3a)
 2π 
 2π 
F C (x , y ,1 ) = FC* (x , y ,2 ) = R (x , y ) + G (x , y )exp  − i
 + B (x , y )exp  + i
.
3 
3 


(3b)
Esta transformación proporciona una manera natural de describir una imagen en color
mediante una imagen de intensidad I(x,y)=FC(x,y,0) y otra de cromaticidad FC(x,y,2),
siendo esta última una imagen compleja. El blanco puede considerarse el término DC de
la transformada de Fourier del color ya que tiene FC(1)=FC(2)=0.
FC(0)
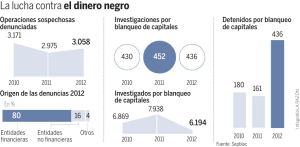
La figura 1 muestra una representación geométrica del color basada en la
transformada de Fourier del color. El eje vertical
representa el valor de la intensidad FC(0), mientras
que el plano perpendicular representa el plano
complejo, con η=Re{FC(2)} y ξ=Im{FC(2)}. Los
diferentes colores generan un cono sólido invertido.
B
A’
Los tonos de gris quedan en el eje vertical. Colores
ρ
con igual tono están situados en la misma posición
G
φ
angular φ, mientras que la saturación del color está
directamente relacionada con el radio ρ. En particular
R
los colores con máxima saturación quedan localizados
A
en la superficie exterior del cono. La sección
horizontal es un círculo donde quedan todos los
colores de igual intensidad. En particular, los colores
que pueden obtenerse como suma de valores positivos
ξ
η
de rojo, verde y azul se encuentran dentro del
triángulo de Maxwell inscrito dentro del círculo de
color, (triángulo RGB en la figura). Los colores que Fig. 1: Representación gráfica del
color basada en la transformada
quedan fuera del triángulo pueden obtenerse como
de Fourier de color.
combinación aditiva de rojo, verde y azul, si alguno
de estos primarios toma un valor negativo.
3. Blanqueo del espectro de color y blanqueo del espectro 3D
La operación de blanqueo del espectro de color consiste en realizar un filtrado tal que el
espectro de la señal filtrada es F‘C(x,y,m)= FC(x,y,m)/|FC(x,y,m)|, de forma que el
resultado es un espectro sólo de fase. De manera análoga se define el blanqueo 3D
aplicado a la transformada de Fourier 3D. La figura 1 muestra el efecto del blanqueo de
color sobre un color representado por el punto A. La normalización del espectro implica
que el nuevo color tiene intensidad unidad, y también que ρ=1. El nuevo color filtrado
A’ se encuentra localizado en la superficie del cono y por tanto tiene máxima saturación.
La figura 2 muestra las componentes de una imagen en color y la imagen filtrada al
blanquear los espectros de color y 3D. La primera fila muestra el objeto test, que se ha
seleccionado con colores poco saturados, como indica la presencia de niveles altos en
las tres componentes. Los objetos (a,b,c) corresponden a las componentes R,G,B de esta
imagen. La segunda fila corresponde al objeto filtrado mediante blanqueo del espectro
de color. La distribución espacial no se altera pero se produce una saturación de los
colores. En estas imágenes se ha visualizado el valor absoluto para evitar los valores
negativos que aparecen al saturarse los colores. Finalmente la tercera fila (g,h,i) muestra
el resultado del blanqueo del espectro 3D. Junto con el aumento de saturación, se
produce el realce de bordes típico del
blanqueo de frecuencias espaciales. La
saturación no es máxima ya que se
produce una mezcla de componentes
espaciales y de color.
La figura 3 muestra el módulo de las
tres componentes de la autocorrelación
3D de las tres imágenes anteriores. En el
primer caso (imagen original) se
obtienen picos de correlación anchos
característicos del filtro espacial clásico,
y se obtienen por igual en los tres
canales, indicando la alta correlación
entre canales. En el segundo caso
(blanqueo del espectro de color) el pico
sigue siendo ancho, pero solamente
aparece en el canal n=0, indicando que
la autocorrelacion está concentrada en el
origen de color como consecuencia del
blanqueo en el eje de color. Finalmente,
en el tercer caso (blanqueo del espectro
3D), aparece de nuevo el pico solamente
en el canal n=0, pero ahora es un pico
muy estrecho ya que también la parte
espacial de la señal se ha concentrado en
el origen. Este resultado indica la
utilidad del filtrado 3D para el
reconocimiento de patrones en color.
Agradecimientos
Fig. 2: Componentes RGB de: (a,b,c) imagen test en
color; (d,e,f) imagen con blanqueo del espectro de
color; (g,h,i) imagen con blanqueo del espectro 3D.
a)
b)
c)
n=0
n=0
n=0
n=1
n=1
n=1
n=2
n=2
n=2
Fig. 3: Componentes en los canales 0,1 y 2 de la
autocorrelación 3D de (a) imagen test en color; (b)
imagen con blanqueo del espectro de color; (c) imagen
con blanqueo del espectro 3D.
Este trabajo ha sido financiado por el Ministerio de Ciencia y Tecnología a través de los
proyectos BFM2000-0036-C02-01 y BFM2000-0036-C02-02. Josep Nicolás agradece
una beca de la Universitat Autònoma de Barcelona.
Bibliografía
[1]
[2]
[3]
[4]
M.S. Millán, J. Campos, C. Ferreira y M. J. Yzuel, Opt. Commun, 73 (1989) 277
M. Guillaume, Ph. Réfrégier, J. Campos y V. Lashin, Opt. Lett. 22 (1997) 1887
J. Nicolás, M. J. Yzuel y J. Campos, Opt. Commun. 184 (2000) 335
J. Nicolás, I. Moreno, J. Campos y M. J. Yzuel, Appl. Opt. aceptado.