áreas y volúmenes de cuerpos en el espacio

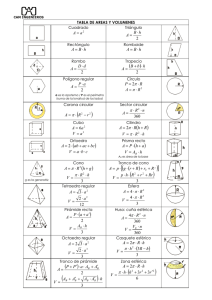
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
1. Área y volumen del ortoedro y del cubo.
1.1. Área y volumen del ortoedro.
1.2. Cálculo de la diagonal del ortoedro.
1.3. Área y volumen del cubo.
2. Área y volumen del prisma. Principio de Cavalieri.
3. Área y volumen del cilindro.
4. Área y volumen de pirámides regulares y conos.
4.1. Área y volumen de la pirámide regular.
4.2. Área y volumen del cono.
5. Área y volumen de troncos y esferas.
5.1. Área y volumen del tronco de pirámide.
5.2. Área y volumen del tronco de cono.
5.3. Área y volumen de la esfera.
6. Área y volumen de poliedros regulares.
7. Resumiendo: tabla de fórmulas.
Los contenidos que vamos a aprender en este tema se ajustan a los contenidos del
Bloque de Geometría de 2º ESO citados en el Decreto 69/2007, de 29-05-2007, por el
que se ordena el currículo de la Educación Secundaria Obligatoria en la Comunidad
Autónoma de Castilla-La Mancha (DOCM 01-06-2007)
Poliedros y cuerpos de revolución. Desarrollos planos y elementos
característicos. Clasificación atendiendo a distintos criterios. Utilización de
propiedades, regularidades y relaciones para resolver problemas del mundo
físico.
Volúmenes de cuerpos geométricos. Resolución de problemas que impliquen
la estimación y el cálculo de longitudes, superficies y volúmenes.
Utilización de procedimientos tales como la composición, descomposición,
intersección, truncamiento, dualidad, movimiento, deformación o desarrollo de
poliedros para analizarlos u obtener otros.
Uso de herramientas informáticas para construir, simular e investigar
relaciones entre elementos geométricos.
APM
Página 1
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
1. ÁREA Y VOLUMEN DEL ORTOEDRO Y DEL CUBO.
1.1. ÁREA Y VOLUMEN DEL ORTOEDRO.
Como ya sabemos, un ortoedro es un paralelepípedo en el que la totalidad de sus
caras son rectángulos.
Para conocer el área del ortoedro, es necesario conocer primero su desarrollo.
Observemos el siguiente ortoedro:
Si lo desarrollamos:
Podemos observar que se trata de seis rectángulos iguales dos a dos.
El área de la base (rectángulo verde) es a∙b.
El área lateral es: Perímetro de la base x altura = (2a+ 2b) x c
Luego, el área del ortoedro es: área bases + área lateral =2ab + 2ac + 2bc.
Por tanto, si tenemos un ortoedro con dimensiones a, b y c, el área será:
Área del ortoedro = 2∙(ab + ac + bc)
APM
Página 2
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Pasemos a calcular el volumen del ortoedro.
Observa la siguiente caja, que es un ortoedro.
¿Cuántos cubitos unidad hay en la figura?
Rellenamos el fondo con cubos, formando una capa de 6 ∙2 = 12 cubitos.
Para rellenar la caja hay que poner tres capas. Por tanto: (6 ∙2) ∙3 = 36 cubitos.
Como el producto a∙b es el área de la base, el volumen del ortoedro es igual al
área de la base por la altura.
Por tanto, si tenemos un ortoedro con dimensiones a, b y c, el volumen será:
Volumen del ortoedro = área base x altura = a∙b∙c
Veamos un ejemplo de cálculo: Una piscina tiene 8 m de largo, 6 m de ancho y
1.5 m de profundidad. Se pinta la piscina a razón de 6 € el metro cuadrado.
a) ¿Cuánto costará pintarla?
b) ¿Cuántos litros de agua serán necesarios para llenarla?
Vamos a hacer un dibujo representativo.
APM
Página 3
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
CUIDADO: Ten en cuenta que la piscina no tiene tapa. Luego la base no hay que
multiplicarla por dos.
El área es:
A=8∙6 +2∙(8∙1,5 + 6∙1,5) = 48+2∙(12+9)=48+2∙21=48+42=90 m2.
Por tanto, costará: 90∙6=540 €.
Para calcular los litros es necesario conocer el volumen:
V=8∙6∙1,5= 72 m3=72000 dm3=72000 litros
1.2. CÁLCULO DE LA DIAGONAL DEL ORTOEDRO.
Veamos el siguiente dibujo de un ortoedro y su diagonal.
Si conocemos a, b y c, es muy fácil calcular la diagonal D del ortoedro.
Vamos a dibujar la diagonal de la base. Si observas el dibujo detenidamente, verás
que se forma un triángulo rectángulo.
Por tanto, si calculamos la diagonal de la base, que vamos a llamar d, y
conocemos la altura c del ortoedro, utilizando el teorema de Pitágoras podemos calcular
D (diagonal del ortoedro).
APM
Página 4
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Vamos a ver un ejemplo. Calcula la diagonal del siguiente ortoedro:
Primero calculamos la diagonal de la base (d), que es un rectángulo de lados 10
cm y 4 cm. Por el teorema de Pitágoras:
d
4 cm
10 cm
d2 = 102 + 42
d2 = 100 + 16
d2 =116
Una vez que conocemos d, por el teorema de Pitágoras tenemos:
D
c = 5 cm
d = 10,77 cm
D2 = 52 + 10,772
D2 = 25 + 116
D2 =141
APM
Página 5
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
1.3. ÁREA Y VOLUMEN DEL CUBO.
Para saber cuál es el área lateral del cubo, es necesario conocer su desarrollo.
Imaginemos que tenemos un cubo y lo desplegamos. Se obtiene lo siguiente:
Por tanto, como un cubo está formado por seis cuadrados iguales, y el área del
cuadrado es lado x lado, entonces llegamos a la conclusión de que:
Si a es la arista del cubo, entonces:
Área cubo = 6∙a2
APM
Página 6
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Vamos a calcular su volumen.
El cubo es un ortoedro particular, que tiene todas sus aristas iguales.
En el ejemplo, el volumen sería: área de la base x altura = 5∙5∙5 = 125 cubitos.
Por tanto, si tenemos un cubo de arista a, el volumen será:
Volumen del cubo = a ∙ a ∙ a = a3
2. ÁREA Y VOLUMEN DEL PRISMA. PRINCIPIO DE CAVALIERI.
Para calcular el área de un prisma, vamos a conocer su desarrollo:
El desarrollo plano de un prisma recto está compuesto por un rectángulo y los dos
polígonos que forman las bases. Uno de los lados del rectángulo coincide con el
perímetro de la base, y el otro, con la altura del prisma.
APM
Página 7
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
El área lateral (área del rectángulo) es igual al perímetro de la base por la altura:
AL = PB · h
El área total es la suma del área lateral y el área de las bases:
ATotal = ABases + ALateral = 2ABases + PerímetroBase · h =
=
Por tanto, si tenemos un prima con apotema de la base a y altura h, entonces:
Área prisma = perímetro∙(apotema+h)
¿Qué ocurre si el prisma es oblicuo?
Las fórmulas utilizadas para calcular la superficie de prismas rectos son válidas
también para prismas oblicuos, porque la altura del prisma coincide con la altura de las
caras laterales. La diferencia es que esa altura no es la misma que la longitud de las
aristas laterales.
APM
Página 8
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Antes de calcular el volumen del prisma, vamos a ver el Principio de Cavalieri.
Principio de Cavalieri: “Si dos cuerpos tienen la misma altura y bases de igual
área, y al cortarlos por cualquier plano paralelo a las bases, el área de las secciones es la
misma, ambos tienen igual volumen”.
Para comprobar el principio de Cavalieri, observamos esta figura:
A la izquierda tenemos un montón de ladrillos iguales, unos encima de otros, y a
la derecha, están los mismos ladrillos desordenados. Es obvio que, en los dos casos, el
volumen que ocupan es el mismo. Observamos que si cortamos con un plano a
cualquier altura, la sección es la misma.
Veamos cuál es el volumen de un prisma.
APM
Página 9
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
El volumen de un prisma de base cualquiera, por el principio de Cavalieri, será
igual que el de un ortoedro con la misma sección, es decir, con la misma área de la base.
VPRISMA = área de la base · altura = AB · h
Si el prisma no es recto, su volumen, según el principio de Cavalieri, será el
mismo que el del prisma recto con igual sección y altura. La única diferencia es que, en
este caso, la altura no coincide con la arista lateral.
Por tanto, si tenemos un prisma con dimensiones a, b y c, el volumen será:
Volumen del prisma = área base x altura = a∙b∙c
3. ÁREA Y VOLUMEN DEL CILINDRO.
A partir del desarrollo del cilindro podemos calcular su área.
Área lateral, AL: Es el área de un rectángulo cuya base es la longitud de la
circunferencia de la base, 2πr, y la altura, h, es la altura del cilindro o generatriz,
g:
AL = 2 ∙ π ∙ r · h
Área de las bases, AB: Es la suma de las áreas de las dos bases. Como las bases
son círculos, cada una tendrá un área:
AB = π ∙ r2
El área total de un cilindro es la suma del área lateral más el área de las dos
bases.
AT = AL + 2 · AB = 2πrh + 2πr2
APM
Página 10
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Por tanto, si tenemos un cilindro de radio r y altura h, el área total será:
Área cilindro = 2πrh + 2πr2 = 2πr∙(h+r)
Para calcular el volumen de un cilindro, vamos a utilizar el principio de Cavalieri.
Dibujemos un cilindro y un prisma recto con la misma altura, bases de igual área
y secciones también de la misma área. Según el principio de Cavalieri, tendrán igual
volumen.
Si el radio del cilindro es r y la altura h, su volumen será:
Vcilindro = AB · h =πr2h
Por tanto, si tenemos un cilindro de radio r y altura h, el volumen será:
Volumen cilindro = área base x altura = πr2h
APM
Página 11
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Veamos un ejemplo: Calcula la cantidad de hojalata que se necesitará para hacer
10 botes de forma cilíndrica de 10 cm de diámetro y 20 cm de altura
Vamos a hacer un dibujo representativo.
En este caso el radio r = 5 cm y la altura h = 20 cm. Entonces, el área del cilindro
es:
A = 2∙π∙5∙(20+5) = 250π = 785,4 cm2
Como tenemos que hacer 10 botes con esas dimensiones, entonces necesitaremos:
785,4∙10 = 7854 cm2 de hojalata
4. ÁREA Y VOLUMEN DE PIRÁMIDES REGULARES Y CONOS.
4.1. ÁREA Y VOLUMEN DE LA PIRÁMIDE REGULAR.
Para calcular el área de una pirámide es necesario conocer su desarrollo.
El desarrollo de una pirámide recta está formado por el polígono de la base y
tantos triángulos isósceles iguales como lados tenga la base.
APM
Página 12
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Su área lateral será la suma de las áreas de los triángulos:
= n∙l ·
Alateral = número triángulos
Abase =
= perímetro base ·
, pues la base es un polígono regular.
Para calcular el área total habrá que sumar al área lateral el área de la base.
Por tanto, si tenemos una pirámide regular (cuya base tiene n lados que miden l
cada uno y apotema a) y con una altura h, entonces:
Área pirámide =
En el caso de que la pirámide no sea recta, al calcular el área lateral debemos tener
en cuenta que la altura es distinta para cada cara, luego calculamos el área de cada una
por separado.
Vamos a calcular, ahora, el volumen de una pirámide. Para ello, consideramos un
prisma y una pirámide con la misma área de la base y la misma altura, h.
Si llenamos la pirámide con arena fina o agua y la vaciamos en el prisma,
comprobamos que para llenar el prisma se necesitaría el contenido exacto de tres
pirámides.
APM
Página 13
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Luego, el volumen de la pirámide es un tercio del volumen del prisma.
Por tanto, si tenemos una pirámide regular (cuya base tiene n lados que miden l
cada uno y apotema a) y con una altura h, entonces:
Volumen pirámide =
APM
Página 14
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
4.2. ÁREA Y VOLUMEN DEL CONO.
A partir de su desarrollo podemos calcular el área de un cono.
Área lateral, AL: Es el área de un sector circular, siendo la longitud del arco la
longitud de la circunferencia de la base. Sabemos que el área de un sector circular es:
Asector circular =
.
Como no conocemos el ángulo n, tenemos que calcular el área del sector circular
de otra manera. Vamos a hacer mediante una regla de tres.
La circunferencia completa tiene una longitud de 2 π g.
El arco correspondiente al sector circular tiene una longitud de 2 π r.
El área del círculo completo es π g2.
Planteemos la regla de tres:
longitud de la circunferencia---------------superficie círculo
longitud del arco---------------------------- superficie del sector
Por tanto, si llamamos x a la superficie del sector, tenemos:
2 π g------------------ π g2
2 π r------------------- x
Luego,
APM
Página 15
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Por tanto, Área lateral = Área sector circular = π r g
Área de la base, AB: Es el área del círculo: AB = π ∙ r2.
El área total de un cono es la suma del área lateral más el área de la base:
AT = AL + AB = πrg + πr2
Por tanto, si tenemos una cono de generatriz g y radio r, entonces:
Área cono = πrg + πr2
Pasemos a calcular el volumen de un cono. Como en apartados anteriores, vamos
a utilizar el principio de Cavalieri.
Consideremos una pirámide y un cono, ambos de altura h, con bases de igual área
y secciones de la misma área.
Según el principio de Cavalieri, tendrán el mismo volumen. Luego, el volumen
del cono será igual, por tanto, a un tercio del área de la base por la altura.
Por tanto, si tenemos un cono de altura h y radio r, entonces:
Volumen cono =
APM
Página 16
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Veamos un ejemplo de cálculo: Para una fiesta, Luis ha hecho 10 gorros de forma
cónica con cartón. ¿Cuánto cartón habrá utilizado si las dimensiones del gorro son 15
cm de radio y 25 cm de generatriz?
Hagamos un dibujo representativo.
CUIDADO: No hay que sumar el área de la base, pues al ser un gorro, no está
tapado. Si estuviera tapado no podrías ponértelo en la cabeza.
El área lateral del cono es: A = π∙15∙25 = 375∙π = 1178,1 cm2.
Como queremos hacer 10 gorros con esas dimensiones, entonces se necesitará:
1178,1∙10 = 11781 cm2 de cartón
5. ÁREA Y VOLUMEN DE TRONCOS Y ESFERAS.
5.1. ÁREA Y VOLUMEN DEL TRONCO DE PIRÁMIDE.
Para calcular el área del tronco de pirámide es necesario conocer su desarrollo.
Observemos el siguiente dibujo:
APM
Página 17
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Como podemos observar el tronco de pirámide se descompone en n trapecios,
siendo n el número de lados de la base.
Por tanto, el área lateral de un tronco de pirámide es la suma de las áreas de los n
trapecios. Es decir, la mitad de la suma de los perímetros de las bases por la apotema.
Área lateral =
Al área lateral se le suma el área de cada base para hallar el área total.
Por tanto, si tenemos un tronco de pirámide con apotema a, entonces:
Área tronco pirámide =Área bases +
Vamos a calcular el volumen del tronco de una pirámide.
Observemos el siguiente dibujo:
APM
Página 18
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
El volumen de un tronco de pirámide se puede calcular mediante la siguiente
fórmula.
Sean S1 y S2 las superficies de las bases del tronco de pirámide y h su altura,
entonces:
5.2. ÁREA Y VOLUMEN DEL TRONCO DE CONO.
Para calcular el área del tronco de cono es necesario conocer su desarrollo.
El desarrollo de un tronco de cono es un trapecio circular y dos círculos.
El trapecio circular tiene por bases las longitudes de las circunferencias.
Base mayor: 2πR
Base menor: 2πr
Altura del trapecio: g
APM
Página 19
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Luego el área lateral es el área del trapecio circular, es decir:
Área lateral = Área trapecio circular = 2 π R + 2 π r 2 ∙ g
AL = (πR + πr)g = πg(R + r) → AL = πg(R + r)
El área total es igual al área lateral más el área de los dos círculos.
AT = πg(R + r) + πR2 + πr2
Por tanto, si tenemos un tronco de cono de radios R y r y altura g, entonces:
Área tronco cono = área bases + área lateral = πR2 + πr2 + πg(R + r)
Vamos a calcular el volumen del tronco de cono.
Observemos el siguiente dibujo:
APM
Página 20
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
El volumen de un tronco de cono se puede calcular mediante la siguiente fórmula.
Sean S1 y S2 las superficies de las bases del tronco de cono y h su altura, entonces:
5.3. ÁREA Y VOLUMEN DE LA ESFERA.
La esfera es un cuerpo redondo que no tiene caras, y está formado por una única
superficie curva. Tampoco tiene desarrollo, como el cilindro o el cono.
La superficie de la esfera se denomina superficie esférica.
Podemos medir su área del siguiente modo:
Imaginamos una esfera cubierta por un cilindro ajustado a ella.
APM
Página 21
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
El área lateral del cilindro es igual que el área de la esfera. Por tanto:
ALATERAL CILINDRO = 2πr · g = AESFERA
Como en el caso de la esfera g = 2r, entonces tenemos que:
AESFERA = 2πr · 2r = 4πr2
Por tanto, si tenemos una esfera de radio r, entonces:
Área esfera = 4πr2
Vamos a calcular el volumen de una esfera. Para ello, consideramos la esfera
dividida en multitud de pequeñas pirámides iguales con vértice común en el centro de la
esfera. La base de cada una de las pirámides es muy pequeña, por lo que podemos
considerarla plana y aplicar la fórmula del volumen de una pirámide.
Así, si llamamos AB al área de la base de la pirámide, su volumen es:
Volumen pirámide =
APM
Página 22
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
El volumen de la esfera es la suma de los volúmenes de todas las pirámides:
Volumen esfera =
=
La suma de las bases de todas esas pirámides será el área total de la esfera (que, como
ya sabemos, es 4πr2). Luego, el volumen de la esfera es:
Por tanto, si tenemos una esfera de radio r, entonces:
Volumen esfera =
Veamos un ejemplo representativo: Un cubo de 20 cm de arista está lleno de agua.
¿Cabría este agua en una esfera de 20 cm de radio?
Vamos a calcular el volumen del cubo.
Volumen cubo = 203 = 8000 cm3
Ahora, vamos a calcular el volumen de la esfera.
Volumen esfera =
cm3
Por tanto, el agua del cubo sí cabría dentro de la esfera.
APM
Página 23
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
6. ÁREA Y VOLUMEN DE POLIEDROS REGULARES.
Las fórmulas para calcular el área y el volumen de un poliedro regular son
complicadas.
El área total de un poliedro se determina calculando el área de una cara y
multiplicando por el número de caras.
Veamos el desarrollo de un tetraedro.
Si queremos calcular el área de un tetraedro, es necesario calcular el área de uno
de los triángulos que lo forman y, a continuación, multiplicar por cuatro.
El desarrollo del cubo o hexaedro ya lo conocemos. Para calcular su área, es
necesario calcular el área de uno de los cuadrados que lo forman y multiplicar por seis.
APM
Página 24
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Veamos el desarrollo del octaedro.
Para calcular su área total es necesario calcular el área de uno de los triángulos
que lo forman y multiplicar por ocho.
El desarrollo del dodecaedro es el siguiente:
Ya sabemos que está formado por doce pentágono regulares. Por tanto, para
calcular su área es necesario calcular el área de uno de los pentágonos y multiplicar por
doce.
APM
Página 25
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Finalicemos con el icosaedro, que está formado por veinte triángulos equiláteros.
Veamos su desarrollo.
Para calcular su área es necesario calcular el área de uno de los triángulos. A
continuación, multiplicar el resultado por veinte.
Veamos cómo calcular el volumen de los poliedros regulares.
Todos los vértices de un poliedro regular equidistan de un punto interior llamado
centro. Haciendo pasar planos por este punto y por todas las aristas, el poliedro queda
descompuesto en tantas pirámides iguales como caras tiene. Para calcular el volumen de
un poliedro será suficiente calcular el volumen de una de estas pirámides y multiplicar
por el número de caras del poliedro.
Ya sabemos que el volumen de una pirámide es
, siendo AB el área de la
base y a la apotema de la pirámide.
Si n es el número de caras, entonces el volumen
APM
.
Página 26
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Si observamos detenidamente, el producto
consecuencia
es el área total del poliedro, y en
, siendo S el área total del poliedro regular y a la apotema del
poliedro regular.
Por tanto, el volumen de un poliedro regular es la tercera parte del producto de su
área por la apotema.
Veamos un ejemplo: Calcula el área total y el volumen de un dodecaedro de 10
cm de arista, sabiendo que la apotema de una de sus caras mide 6,88 cm.
Como hemos visto anteriormente, no es necesario conocer las fórmulas. Si
pensamos un poco podremos resolver el ejercicio.
Las caras de un dodecaedro son pentágonos regulares. El ejercicio nos indica que
el lado del pentágono mide 10 cm y la apotema 6,88 cm.
6,88 cm
10 cm
Sabemos de temas anteriores, que el área de un pentágono regular es la mitad del
producto del perímetro por la apotema.
Por tanto:
APM
Página 27
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Luego:
Si utilizamos la fórmula que aparece en la tabla del siguiente apartado, obtenemos
el mismo resultado:
Para calcular el volumen vamos a utilizar la fórmula.
APM
Página 28
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
7. RESUMIENDO: TABLA DE FÓRMULAS.
P es el perímetro de la
base
a es la apotema de la
base
h es la altura
P y P’ son los
perímetros
de las bases
a es la apotema
Cubo
Cilindro
A = 6 · a2
A = 2 ∙ π · R · (h + R)
V = a3
Ortoedro
V = π · R2 · h
Cono
A = 2 · (a·b + a·c + b·c)
A = π · R∙ g + π · R2
V=a·b·c
prisma recto
V = π · R2 · h / 3
tronco de cono
A = P · (h + a)
A = π r2 + π R2+π g·(r+R)
V = AB · h
V = (AB+AB'+√AB∙√AB') · h/3=
= π · h · (R2+r2+R·r) / 3
tronco de pirámide
Esfera
A=½(P+P')·a+AB+AB'
A = 4 ∙ π · R2
V = (AB+AB'+√AB∙√AB') · h/3
V = 4 ∙ π · R3 / 3
Pirámide recta
A = P · (a + a') / 2
a es la apotema de la base.
a’ es la apotema de la pirámide
P es el perímetro de la base
APM
V = AB · h / 3
Página 29
ÁREAS Y VOLÚMENES DE CUERPOS EN EL ESPACIO
Sea a la arista de estos poliedros regulares. Entonces:
Nombre
Área de una cara
Área total
Apotema
Volumen
Tetraedro
Octaedro
Icosaedro
Hexaedro o
cubo
Dodecaedro
APM
Página 30