λ μ λ ρ ρ ρ

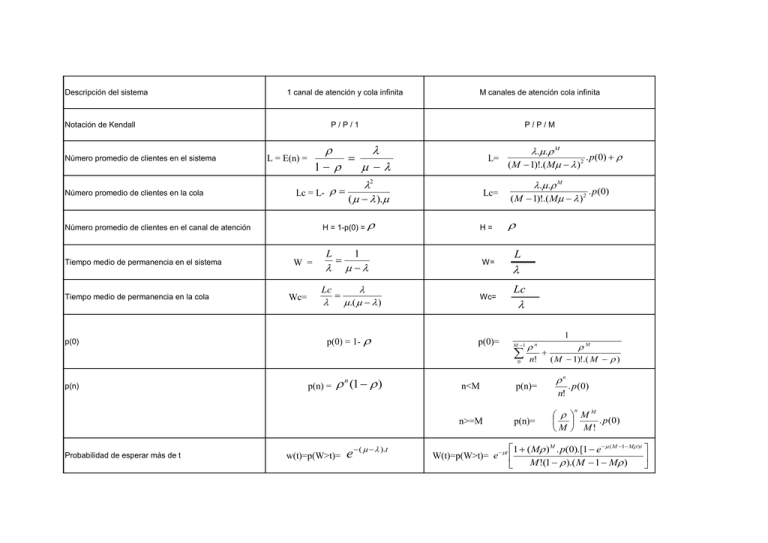
Descripción del sistema
1 canal de atención y cola infinita
M canales de atención cola infinita
P/P/1
P/P/M
Notación de Kendall
Número promedio de clientes en el sistema
Número promedio de clientes en la cola

L = E(n) =
1 
Tiempo medio de permanencia en la cola
p(0)
.. M
. p(0)  
L=
( M  1)!.( M   ) 2
 
2
Lc = L-  
(    ).
W =
Wc=
L

Lc


H=

1
 
W=


.(    )
Wc=
p(0) = 1- 
.. M
. p(0)
( M  1)!.( M   ) 2
Lc=
H = 1-p(0) = 
Número promedio de clientes en el canal de atención
Tiempo medio de permanencia en el sistema


L

Lc

p(0)=
1
M 1

0
p(n)
p(n) =
 n (1   )
n<M

n
n!
p(n)=

M
( M  1)!.( M   )
n
n!
. p ( 0)
M
   M
. p ( 0)


 M  M!
n
n>=M
Probabilidad de esperar màs de t
w(t)=p(W>t)=
e  (    ).t
W(t)=p(W>t)= e
p(n)=
 t
1  ( M ) M . p(0).[1  e   ( M 1 M )t 


M !(1   ).( M  1  M )

