Lección 5. Escorrentía Concepto. Ciclo de la escorrentía. Cuenca

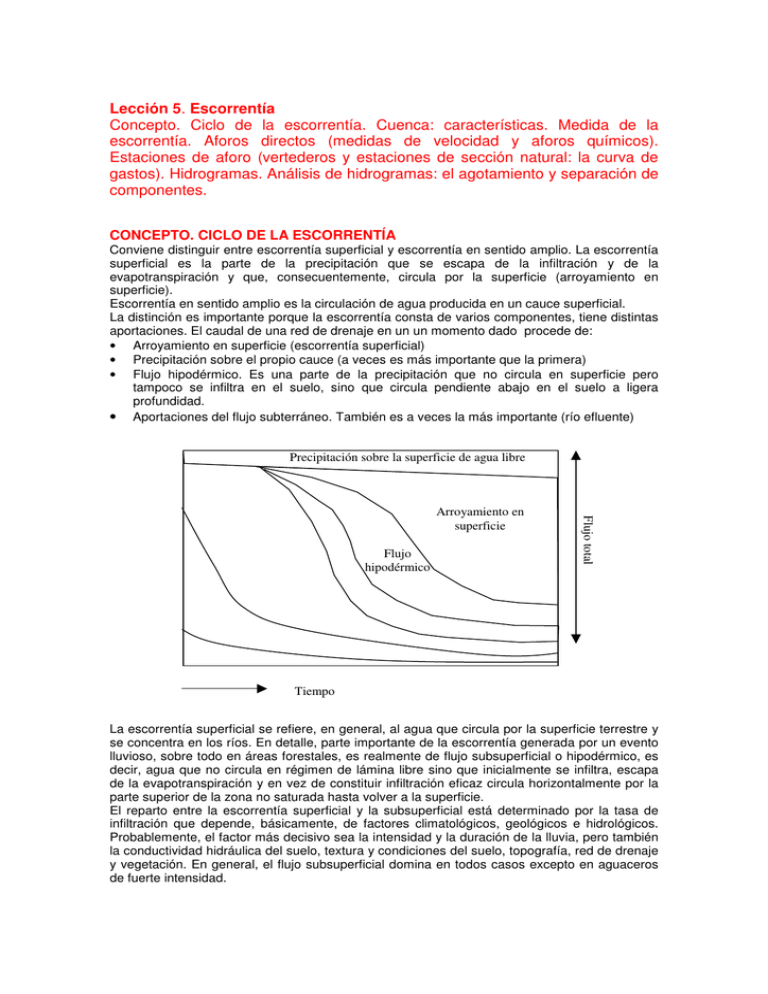
Lección 5. Escorrentía
Concepto. Ciclo de la escorrentía. Cuenca: características. Medida de la
escorrentía. Aforos directos (medidas de velocidad y aforos químicos).
Estaciones de aforo (vertederos y estaciones de sección natural: la curva de
gastos). Hidrogramas. Análisis de hidrogramas: el agotamiento y separación de
componentes.
CONCEPTO. CICLO DE LA ESCORRENTÍA
Conviene distinguir entre escorrentía superficial y escorrentía en sentido amplio. La escorrentía
superficial es la parte de la precipitación que se escapa de la infiltración y de la
evapotranspiración y que, consecuentemente, circula por la superficie (arroyamiento en
superficie).
Escorrentía en sentido amplio es la circulación de agua producida en un cauce superficial.
La distinción es importante porque la escorrentía consta de varios componentes, tiene distintas
aportaciones. El caudal de una red de drenaje en un un momento dado procede de:
• Arroyamiento en superficie (escorrentía superficial)
• Precipitación sobre el propio cauce (a veces es más importante que la primera)
• Flujo hipodérmico. Es una parte de la precipitación que no circula en superficie pero
tampoco se infiltra en el suelo, sino que circula pendiente abajo en el suelo a ligera
profundidad.
• Aportaciones del flujo subterráneo. También es a veces la más importante (río efluente)
Precipitación sobre la superficie de agua libre
Flujo
hipodérmico
Flujo total
Arroyamiento en
superficie
Tiempo
La escorrentía superficial se refiere, en general, al agua que circula por la superficie terrestre y
se concentra en los ríos. En detalle, parte importante de la escorrentía generada por un evento
lluvioso, sobre todo en áreas forestales, es realmente de flujo subsuperficial o hipodérmico, es
decir, agua que no circula en régimen de lámina libre sino que inicialmente se infiltra, escapa
de la evapotranspiración y en vez de constituir infiltración eficaz circula horizontalmente por la
parte superior de la zona no saturada hasta volver a la superficie.
El reparto entre la escorrentía superficial y la subsuperficial está determinado por la tasa de
infiltración que depende, básicamente, de factores climatológicos, geológicos e hidrológicos.
Probablemente, el factor más decisivo sea la intensidad y la duración de la lluvia, pero también
la conductividad hidráulica del suelo, textura y condiciones del suelo, topografía, red de drenaje
y vegetación. En general, el flujo subsuperficial domina en todos casos excepto en aguaceros
de fuerte intensidad.
Cuando estos flujos alcanzan algún canal de la red de drenaje natural y se une al flujo de base
del mismo, originado por la descarga de aguas subterráneas, el conjunto circula por dicha red
de acuerdo con las leyes de la hidráulica de cauces naturales.
De alguna manera, la escorrentía superficial tiene carácter residual de los restantes procesos
hidrológicos, esencialmente estocásticos, sujetos a una gran cantidad de variables no
controladas, por lo que, realmente, la escorrentía superficial carece de una ley fundamental que
rija su comportamiento, por lo que para su análisis y evaluación es necesario recurrir, en la
mayor parte de los casos, a la teoría de sistemas y a la estadística.
Los datos de partida se obtienen en las denominadas estaciones de aforos, o puntos de
control, en donde se realizan mediciones de caudales, por muy diversas técnicas, que se
denominan aforos o medidas hidrométricas.
CUENCA: características
Es una superficie tal que el agua de precipitación que cae sobre cualquier punto de la misma
circula hacia el cauce considerado. Los límites son las divisorias de aguas y se representan por
líneas de cota.
El concepto de cuenca superficial no es el mismo que de cuenca subterránea, y las divisorias
no coinciden.
Límite de cuenca
superficial
Límite de cuenca
subterránea
En el límite de las cuencas subterráneas no influye la topografía, sino razones geológicas.
Necesidad de regulación de la cuenca
La respuesta de una cuenca a la precipitación depende de numerosos factores (topografía,
permeabilidad de los materiales, etc..) y se manifiesta en diferencias de variación de caudal.
Q
Q
t
t
La figura de la izquierda es típica de cuencas con materiales poco permeables, en la que
pueden esperarse inundaciones y crecidas que provocan erosionabilidad y pérdida de suelo. La
cuenca no se autorregula y es necesario regularla artificialmente mediante embalses. En la
figura de la derecha, típica de cuencas bien reguladas naturalmente, el caudal base es
aproximadamente constante.
MEDIDA DE LA ESCORRENTÍA
Los datos hidrométricos deben ser fiables y continuos; para ello se requiere de un periódico y
sistemático contraste y mantenimiento de las estaciones, y un diseño previo de la red de
observación que debe ser lo suficientemente densa como para no permitir la pérdida de
información básica pero no tanto como para representar un excesivo coste, mayor complejidad
de mantenimiento y la obtención de datos no realmente representativos. Un aspecto
interesante a destacar es que, dado precisamente el carácter estocástico del proceso, se
requieren series temporales de larga duración para realizar interpretaciones del funcionamiento
del sistema poco influenciadas por situaciones anecdóticas y poco representativas, y también,
curiosamente, para poder interpretar y enmarcar adecuadamente, este tipo de situaciones. Por
esta razón, el mantenimiento eficiente de la red debe establecerse como norma, y debe estar
sujeta a un proceso continuo de optimización.
Los aforos continuos permiten conocer las variaciones de caudal con el tiempo. Es más sencillo
medir una variable que se relacione con el caudal, como es la altura de la lámina de agua.
Se mide mediante: Escala limnimétrica o limnímetro, limnígrafo, sensores de presión.
Los aforos directos consisten en determinar el caudal de un curso en un momento dado. Hay
de dos tipos: basados en la velocidad del agua (flotador y molinete) y aforos químicos(caudal
constante, inyección instantánea).
Tipos de limnígrafos
Los principales tipos de limnígrafos son los de flotador y los neumáticos o de presión.
Los limnígrafos de flotador consisten básicamente en un flotador que sube o baja según las
oscilaciones del nivel del agua y que por medio de un contrapeso y una polea mueve un lápiz o
una plumilla de tinta que marca las variaciones en el limnigrama.
En los limnígrafos neumáticos el lápiz se mueve por la presión o carga de agua sobre un
sensor de presión que se coloca en el fondo del río, comunicando con el detector de presiones
por un tubo de pequeño diámetro, flexible y resistente.
Sin duda, los limnígrafos de mayor interés son los de presión, equipados con un transductor de
presiones y sistema de almacenamiento de datos en un data logger, o bien la trnsmisión de
datos en tiempo real mediante un equipo emisor. El elevado coste de este sistema hace que
los limnígrafos de flotador sigan siendo muy utilizados.
Para una sección dada, existe una relación entre el caudal y la altura de la lámina de agua, Q =
f (h), que se denomina curva de gastos. La curva de gastos se determina experimentalmente
por medidas repetidas de caudales y alturas en diversas condiciones. A partir de ella, basta con
medir la altura para determinar el caudal, o lo que es lo mismo, basta con determinar la
variación de la altura del agua con el tiempo, para obtener la variación de los caudales con el
tiempo.
1,4
Caudal, en m3/seg
1,2
1,0
0,8
0,6
0.4
0,2
0
10
20
30
40
50
Altura la lámina de agua, en cm
60
70
Normalmente, la curva de gastos se obtiene mediante el dibujo de una curva suave que se
ajuste lo mejor posible a los puntos obtenidos por los pares de valores (hi, Qi), pero también se
puede hacer un ajuste estadístico para obtener la ecuación de la curva que normalmente es
una parábola de segundo grado, del tipo:
2
Q = ah + bh +c
En la que los parámetros a, b y c se obtienen por ajuste de mínimos cuadrados.
a
Otros ajustes de la curva puden ser a leyes exponenciales del tipo h = h0·Q o potenciales de la
A
forma Q = (h - h0) , que tienen la ventaja de que representadas, en papel semilogarítmico la
primera o doblelogarítmico la segunda, la curva de gastos tiene la forma de una recta.
Altura del agua (cm, m)
Aforo por medición de la lámina de agua
A partir de la curva de gastos Q = f ( h) el caudal se determina mediante la medición de la
altura de la lámina de agua.
Estas mediciones se pueden realizar con carácter esporádico, con cierta periodicidad o en
continuo. Para los dos primeros casos se utilizan los limnímetros y para las medidas en
continuo los limnígrafos.
Un limnímetro es, en esencia, una escala graduada que se coloca normalmente adosada a la
pared del cauce, si la hubiere, como es el caso de un puente, por ejemplo, o en el cajero de la
estación de aforos, si está construída. Con objeto de evitar errores en la lectura que pudieran
ser producidos por los agentes atmosféricos o por la propia corriente de agua, los limnímetros
se suelen colocar en el interior de pozos unidos al cauce por medio de tuberías, lo que requiere
un trabajo continuo de mantenimiento para evitar los arrastres sólidos de la corriente puedan
embozar o taponar dichas tuberías.
Tanto si la lectura del limnímetro se realiza con carácter esporádico como periódico el principal
inconveniente que presenta este método es que no se pueden controlar las variaciones de
altura y, por tanto de caudal, que se experimentan entre dos medidas, salvo que estas medidas
se realicen con una ventana temporal reducida, de tipo diario como mínimo, lo que requiere de
una persona encargada de dicha tarea. En los episodios de crecida o avenidas este periodo
debiera ser mucho más reducido.
Desde un punto de vista práctico, es recomendable que todos los caracteres de la escala
(marcas y números) estén grabados o resaltados para evitar que con el tiempo desaparezcan.
Normalmente, las escalas están construidas en plástico, fundición o cerámica.
De mucho más interés son los limnígrafos, que permiten obtener medidas continuas de la
variación de la altura del agua y, por tanto, del caudal. Es decir, se obtiene una curva h = f (t),
que se denomina limnigrama (figura 2), que no es más que el registro sobre un papel adosado
a un tambor giratorio de una plumilla solidaria con un mecanismo sensible a las variaciones de
nivel.
Tiempo (minutos, horas, días)
Figura 2. Ejemplo de limnigrama
En los limnígrafos convencionales, la escala de tiempo es variable en función del mecanismo
empleado pero normalmente la duración es de una semana, quince días o un mes.
La curva del limnigrama, por sí misma, no da información cuantitativa sobre la variación de
caudales si no se coteja con la curva de gastos. La curva resultante Q = f (t) que representa la
variación de los caudales con el tiempo se denomina hidrograma.
Para evita distorsiones, existen las estaciones de aforo de tipo vertedero, en las que se
modifica la sección natural del río, canalizando un tramo con paredes y fondo regulares e
independizando la lámina de agua de manera que el caudal sólo dependa de la altura de la
lámina y no de la pendiente. Para ello se utilizan semimódulos denominados vertederos, que
pueden ser de varios tipos. Para cauces pequeños y de caudales bajos se utilizan los
denominados vertederos de pared o de lámina delgada, que consisten en una chapa metálica
de unos 5 mm de espesor.
En cada vertedero hay una fórmula que da el caudal en función de la altura de la lámina de
agua y de las características del vertedero.
Para ríos de caudal más alto se usan los denominados vertederos de pared gruesa, que
pueden ser de dos tipos: de pantalla y de escalón. Se construyen de hormigón y tienen como
función laminar el caudal. Los de pantalla son semejantes a los metálicos, mientras que los de
escalón no presentan obstáculos sino un escalón que rompe la lámina de agua de modo que
no se acumulen acarreos del río.
En áreas donde son previsibles importantes variaciones estacionales de caudal conviene hacer
un doble vertedero, uno denominado canal principal y otro denominado canal de estiaje.
Aforo por medición de la velocidad de flujo
El caudal que circula por una cierta sección puede calcularse a partir de la velocidad del agua
en dicha sección, ya que se cumple que Q = S·v.
La medición de la velocidad se realiza por dos procedimientos fundamentales: flotadores y
molinetes.
El aforo mediante flotador es un sistema rudimentario pero rápido y muy útil para medidas
puntuales. El flotador puede ser una botella lastrada o cualquier objeto que flote o
preferiblemente que se hunda ligeramente en la lámina de agua, ya que la velocidad en la
superficie es de alrededor de 0,80 a 0,95 la velocidad media.
En la práctica, hay que seleccionar un tramo recto y homogéneo del cauce de una longitud
mínima del orden de cinco a diez metros, procurando que la sección final sea de geometría
sencilla, asimilable a una sección rectangular, de manera que su medida se pueda hacer con la
simple medida de la anchura del cauce y del espesor de la lámina de agua. El flotador debe
aplicarse unos metros antes de la sección inicial del tramo seleccionado con objeto de que la
velocidad del mismo se iguale a la del agua y, sobre todo, que permita iniciar, mediante un
cronómetro, la medida del tiempo que el flotador tarda en recorrer el tramo completo.
Si la anchura del cauce es grande conviene dividirlo en franjas y medir la velocidad en cada
una de estas franjas y calcular luego la velocidad media. También es recomendable repetir
varias veces cada medida y promediar los tiempos obtenidos.
De mayor fiabilidad son las determinaciones de la velocidad del agua mediante un instrumento
denominado molinete que consiste básicamente en una hélice sumergida que se orienta en la
dirección de los filetes líquidos que gira por la presión debida a la velocidad del agua. El eje de
esta hélice transmite su movimiento, por medio de un sistema de engranaje, a un excéntrico
que establece sucesivos contactos en un circuito eléctrico, que transmite las indicaciones a un
contador de vueltas, que se hacen más ostensibles intercalando un timbre o alguna otra señal
visual o auditiva.
La velocidad se determina en función del número de vueltas, según las características del
modelo que se utilice y con arreglo a fórmulas o parámetros determinados por la casa
constructora del aparato. La ecuación general de calibrado es del tipo v = a + b, en la que
son las revoluciones por minuto obtenidas en el contador, y a y b son coeficientes que
dependen del tipo de hélice utilizada.
Si el río es vadeable, el molinete se monta en una varilla que se va apoyando en el fondo, a
altura variable sobre la misma, de acuerdo con el número de observaciones que se vayan a
hacer en cada perfil. El molinete debe colocarse aguas arriba del operador y a la mayor
distancia posible a fin de que no influya en la medida la perturbación que pueda ocasionar el
propio operador.
Si el río no es vadeable, se puede utilizar el sistema de cable y canastilla. Consiste en un cable
tendido de una orilla a otra y anclado en ellas, con apoyo de castilletes y del que se suspende
una canastilla que pueda correr a lo largo del cable y que pueda albergar a una o dos
personas. Desde la canastilla se cuelga el molinete con un cable o se maneja con una varilla.
Otra alternativa es realizar las medidas desde un puente con la ayuda de un torno.
Variaciones de la velocidad
El principal inconveniente de los métodos de medida de la velocidad es que ésta no es
uniforme sino variable, tanto en planta como en alzado, por lo que se requiere realizar una
serie de medidas en diversos puntos de la sección transversal.
Las líneas de igual velocidad se denominan líneas isotacas, cuya distribución se puede ver en
los ejemplos de las figuras 3 y 4.
Figura 3. Planta y perfil de las velocidades en
un cauce natural
Figura 4. Vista frontal de las
isotacas
La curva que adopta la variación de velocidades en una vertical se asemeja a una parábola de
eje horizontal, de forma que el máximo (del orden de 1,2 v) se produce a 0,2 h de la superficie.
Se puede tomar como velocidad media en la vertical la del punto situado a 0,6 h.
Procedimiento operativo
El método más fiable pero también el más laborioso sería dibujar las curvas isotacas por
interpolación de datos y asociar a la franja comprendida entre dos isotacas la velocidad media
de ambas.
En la práctica, se suele dividir el cauce en secciones verticales (figura 5) en cuya mediana se
determina la velocidad en varios puntos, o bien para determinar una velocidad media aplicable
a toda la sección o bien para aplicar cada valor de velocidad a la subsección en que se haya
determinado.
Distribución en secciones de un cauce
Si la velocidad medida en la subsección rayada, de superficie Si, es vi, el caudal que circula por
dicha sección es:
Qi = Si · vi
El caudal total que circula por la sección será:
Q=
S i vi
Aforos químicos
Si en un curso de agua se hace una inyección instantánea de un colorante en todo el ancho de
una sección transversal, la señal coloreada, que en el instante inicial sería una línea recta
perpendicular a la corriente, se iría trasladando hacia aguas abajo debido al movimiento del
agua, al mismo tiempo que iría ensanchándose debido a la difusión de la materia colorante;
asimismo, y causa de esta difusión, el color iría rebajándose, quedando más intenso en la parte
central y más débil en los bordes. Dado que la velocidad en las orillas es menor que en el
centro del cauce, la faja antes citada se convertira en una punta de flecha que se irá
agudizando a medida de la marcha.
Un observador colocado en un punto cualquiera aguas abajo podría dibujar un diagrama que
relacionase la intensidad de coloración con el tiempo, obteniendo un dibujo similar la
hidrograma de un aguacero. La ordenada máxima de este diagrama (la punta) dependerá
fundamentalmente de a distancia del observador al punto de inyección, ya que a mayor
alejamiento la difusión hace que la coloración se vaya rebajando. Las muestras que obtendría
este observador no serían nunca de igual concentración, obteniendo siempre un máximo que
sería tanto menos elevado cuanto más alejado esté el punto de inyección.
Si la inyecciónde colorante se efectuase, en lugar de manera instantánea, de forma continua
durante un periodo suficiente de tiempo, el diagrama obtenido sería la suma de varios
diagramas elementales, decalado cada uno del siguiente un intervalo de tiempo infinitamente
pequeño.
Si el tiempo de inyección es mayor que el de paso de la nube coloreda, se producirá un estado
de equilibrio, apareciendo una meseta durante cuyo intervalo de tiempo la intensidad de
coloración de la nube permanece constante y máxima. El diagrama así obtenido sería similar al
de un aguacero en el que el tiempo de duración del mismo sea superior al de concentración de
la cuenca.
Basados en las consideraciones anteriores, los métodos de aforo de tipo químico son
fundamentalmente dos: métodos de inyección continua o en régimen constante y método de
integración o de inyección instantánea.
Método de inyección continua
En un cierto punto del cauce (estación de inyección) se inyecta a caudal constante (q) una
disolución del trazador con una concentración C conocida y notablemente superior a la
concentración C0 de dicho trazador en el agua del río, si lo hubiere.
La inyección se puede hacer con la ayuda de un frasco de Mariotte o preferiblemente mediante
un inyector de nivel constante, si el caudal del río es apreciable. Si se procede
cuidadosamente, la inyección manual puede dar también buenos resultados.
Aguas abajo, en la estación de medida, el trazador llegará con una concentración inicialmente
baja hasta que se alcanza el régimen permanente correspondiente a la meseta anteriormente
referida (figura 6).
Si es Q el caudal que circula por el río, q el caudal de trazador inyectado, Q+q es el caudal en
la estación de muestreo, C la concentración del trazador en la estación de inyección y Cm la
concentración en la estación de muestreo, según la ecuación de continuidad, y en el supuesto
Q ⋅ C 0 + q ⋅ C = (Q + q ) ⋅ C m
de que no haya ni aportes ni pérdidas entre ambas estaciones, se puede escribir:
De donde:
Q=q
C − Cm
Cm − C0
Dado que C0 es despreciable de por sí y que Cm tiene poca importancia respecto a C, se puede
escribir:
C
Cm
Meseta de
concentración
Concentración
Q=q
Tiempo
Curva de concentración en el río en un aforo químico a caudal constante
Conviene asegurarse de que, una vez conseguida la meseta, la concentración del trazador
debe ser la misma en todos los puntos de la corriente en que se efectúe el muestreo. Para
lograr esto se precisa que los puntos de inyección y muestreo estén suficientemente alejados,
pero no demasiado con el fin de reducir el tiempo de inyección y, por tanto, ahorrar trazador.
Por otra parte, hay que comprobar que el trazador no sea retenido por el terreno o la materia
orgánica entre las dos esatciones, es decir, que la cantidad de trazador que atraviesa que la
sección de control sea igual a la cantidad de trazador que se inyecta, en el intervalo en que
dura la meseta.
Método de inyección instantánea
Este método consiste en la inyección total del trazador en un corto espacio de tiempo. En la
sección de control se van tomando muestras sucesivas que marquen la variación de
concentración del trazador desde que empieza a presentarse hasta que desaparece
totalmente.
Concentración
4
5
6
3
7
2
C3
C2
8
1
∆t
Tiempo
∆t
Curva de concentración en el río en un aforo con trazador instantáneo
En este caso, la curva de concentración presenta la forma de una campana de Gauss, aunque
generalmente de forma asimétrica.
Si consideramos la corriente de agua dividida en un número determinado de tubos imaginarios
de sección suficientemente pequeña para que la concentración de trazador (c) existente en un
momento determinado no presente ningún gradiente, por uno de estos tubos pasará una
fracción de caudal (dQ) y una fracción (dM) de la masa total de trazador inyectado.
Se verifica que:
Siendo C la concentración media, según:
dM = C ⋅ dQ
De manera que:
Q=
M
C = c dt
c dt
O bien:
Q=
M
∆t c
Como los intervalos t son constantes y la campana de la figura 7 puede considerarse a
grandes rasgos simétrica, el denominado puede ser sustituido por T·C, sinedo T el tiempo total
base de la onda de llegada, de manera que:
Q=
M
TC
También se puede resolver la integral calculando el área de la figura 7, que se calcula de la
siguiente manera: si tomamos, por ejemplo, el intervalo comprendido entre los muestreos 2 y 3,
en los que se han determinado las concentraciones respectivas c2 y c3, el área que
corresponde es el siguiente:
El área total será:
c + c3
c + c4
c + c8
c1 + c 2
∆t + 2
∆t + 3
∆t + ..... + 7
∆t
2
2
2
2
(c − c 2 ) ⋅ ∆t c 2 + c3
s = c 2 ⋅ ∆t + 3
=
∆t
2
2
S = c dt =
Para calcular la superficie del primer y último intervalos, se admite una muestra anterior y
posterior, respectivamente, de concentración cero.
Desde el punto de vista práctico, si se aplica la fórmula de la concentración media, bastaría con
tomar n muestras a intervalos regulares de tiempo y todas ellas del mismo volumen, de manera
que se pueden mezclar y realizar un solo análisis de la mezcla para obtener la concentración
media. Naturalmente, se debe estar seguro de cuales son la primera y última muestra del paso
de la nube de trazador. Para aplicar el método de integración se requieren muestras distintas a
intervalos fijos de tiempo y un análisis de cada una de ellas.
Tipos de trazadores
Se dividen en dos grandes grupos: químicos y radioactivos.
Los trazadores químicos más utilizados son el dicromato sódico, la fluoresceína y la rodamina
B. Las condiciones que deben cumplir son que el trazador disuelto no quede perturbado en su
marcha ni por los materiales del lecho del río ni por las características de la corriente, que
pueda efectuarse su determinación cuantitativa a bajas concentraciones con suficiente
exactitud y de forma simple, que sea suficientemente soluble en agua y que que tenga baja
toxicidad (se requiere precaución con el dicromato potásico).
En cuanto a los trazadores radioactivos, los más utilizados son el el Br-82, como BrNH4 y el I131, como NaI. Sus características deben ser las mismas que las mencionadas para los
trazadores químicos pero, además, deben tener baja radiotoxicidad, corto periodo de
semidesintegración, alta actividad específica de suministro, facilidad de adquisición y precio
reducido.
HIDROGRAMA
Es la representación de la variación del caudal con el tiempo.
El hidrograma correspondiente tendrá formas distintas según las aportaciones que
alimenten al caudal.
a) Todo el caudal es debido a la precipitación sobre el propio cauce. El resto del agua
es retenida por el suelo
b) Las aportaciones son debidas tanto a la precipitación sobre el propio cauce como
al fluo hipodérmico
c) Debidas a la precipitación, al flujo hipodérmico y a la escorrentía superficial
d) Aporte de todo lo anterior más el aporte de los acuíferos
Hidrograma de una crecida
Q
P
Punta
cg
CC
CD
TR
CA
TC
TB
Tconc
t
P
Cg
CC
CD
CA
TR
TC
TB
Precipitación
Centro de gravedad de la precipitación
Curva de crecida
Curva de descenso
Curva de agotamiento
Tiempo de respuesta
Tiempo de concentración
Tiempo base
Tconc Tiempo de concentración
Es el tramo final del hidrograma, en el que hay un cambio de pendiente. En esta zona
del hidrograma las aportaciones son debidas a las aguas subterráneas, de forma que
su estudio puede proporcionar información sobre el comportamiento de los acuíferos.
Durante el agotamiento, la ley de decrecimiento del caudal responde a la ecuación de
Maillet:
α
en donde Qo es el caudal al comienzo del agotamiento, t es el tiempo transcurrido
desde el inicio del agotamiento y es el coeficiente de agotamiento (días-1).
Por definición, α es el la inversa del tiempo necesario para que el caudal descienda
una fracción -ésima, de manera que si el caudal desciende rápidamente,
es muy
grande, y si desciende lentamente, es pequeño.
α
α
Que es la ecuación de una recta en la que t y Qt son las variables, de modo que se
puede representar en papel semilogarítmico, lo que dará una una recta de pendiente
negativa cuyo valor es -0.4343α, que corresponde a (lg Q2 - lg Q1) / (t2 - t1).
En el hidrograma se puede separar la aportación de agua subterránea y distinguirla de
la escorrentía directa. Para ello hay varias soluciones:
a) Trazar una paralela al eje de abscisas por el punto del inicio de la crecida
b) Trazar una línea entre el punto del inicio de la crecida y el punto de inicio del
agotamiento
c) Trazar una curva entre los dos puntos anteriores, aproximadamente, haciendo
pasar el mínimo coincidiendo con la punta.
Pero el método más aceptado es el de Barnes, que consiste en prolongar la curva de
agotamiento hasta la punta, y desde ahí otra recta hasta el inicio de la crecida.