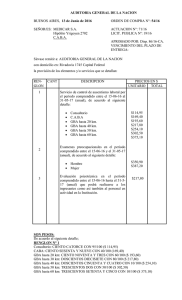
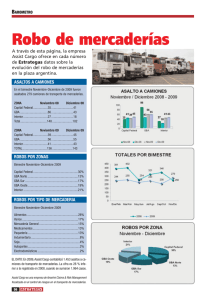
Tema 6 (3): Márgenes de estabilidad relativa

Tema 6 (3): Márgenes de
estabilidad relativa
¡BA ⇒BC!
Im
−1
Mf
Re
GBA ( jωc )
ωc
GBA ( jω )
−1
Introducción
z
Criterio de Nyquist:
z
z
z
z
Estabilidad en bucle cerrado a partir de
propiedades de bucle abierto.
Basado en modelo de G(s) o en datos de la
respuesta frecuencial experimental.
Aplicable a sistemas con retardos.
Criterio gráfico:
z
z
Proporciona medida de la lejanía de la inestabilidad.
Incertidumbres: dos sistemas son parecidos si sus
respuestas frecuenciales son parecidas.
Regulación Automática
M.G. Ortega
Criterio de Nyquist
z
Enunciado:
Un sistema en BUCLE CERRADO es estable
⇔
la imagen de GBA(s) sobre el contorno de
Nyquist rodea al -1 en sentido antihorario
tantas veces como polos de GBA(s) haya en el
SPD abierto.
Regulación Automática
M.G. Ortega
Criterio de Nyquist reducido
z
Enunciado:
Si GBA(s) no tiene polos en el SPD abierto, GBC(s) es estable
si y sólo si
el Nyquist de GBA(s) no engloba al -1
Im
−1
Re
GBC(s) ESTABLE
Regulación Automática
Im
−1
Re
GBC(s) INESTABLE
Im
−1
Re
GBC(s) ESTABLE
M.G. Ortega
Criterio de Nyquist reducido
z
GBC(s) ESTABLE
Idea intuitiva:
Im
−1
RESPUESTAS EN B.C.
Re
GBA ( jω )
t
Im
−1
GBA ( jω )
Regulación Automática
Re
t
M.G. Ortega
Márgenes de estabilidad relativa
z
Permiten medir la proximidad de la inestabilidad.
z
Necesarios por estabilidad frente incertidumbre y
por comportamiento.
z
En este curso:
z
z
z
Margen de ganancia
Margen de fase
Se miden en GBA(s),
pero dan información de
la estabilidad de GBC(s)
Existen otras posibilidades (cursos de especialización).
Regulación Automática
M.G. Ortega
Márgen de ganancia (MG)
z
Definición:
Variación relativa de la ganancia del sistema en
bucle abierto para el sistema en bucle cerrado
alcance el límite de la estabilidad
D
−1
ω180
GBA ( jω )
Im
Re
1
Mg =
D
D = GBA ( jω180 ) donde ω180 t.q. ∠GBA ( jω180 ) = − 180 º
Basado en Criterio de Nyquist reducido: válido
sólo si GBA(s) no tiene polos en el SPD abierto.
Regulación Automática
M.G. Ortega
Márgen de ganancia (Mg)
z
Definición:
1
GBA ( jω180 ) =
Mg
Mg =
Im
1
donde ω180 t.q. ∠GBA ( jω180 ) = − 180 º
GBA ( jω180 )
G BA ( jω ) dB
ω180
0 dB
−1
M g > 0dB ( > 1)
Re
ω180
GBA( jω)
GBC ( s ) ESTABLE
ω ( rad / s )
∠G BA ( jω )
− 180 º
ω ( rad / s )
ω180
GBC(s) ESTABLE ⇔ Mg > 1 (0 dB)
Regulación Automática
M.G. Ortega
Márgen de ganancia (Mg)
z
Definición:
GBA ( jω180) =
1
Mg
Mg =
Im
1
donde ω180 t.q. ∠GBA ( jω180 ) = − 180 º
GBA ( jω180 )
G BA ( jω ) dB
M g < 0dB (< 1)
ω ( rad / s )
0 dB
Re
ω180
−1
ω180
∠GBA ( jω )
GBA( jω)
− 180 º
ω ( rad / s )
ω180
GBC ( s ) INESTABLE
GBC(s) ESTABLE ⇔ Mg > 1 (0 dB)
Regulación Automática
M.G. Ortega
Márgen de fase (Mf)
z
Definición:
Variación relativa de la fase del sistema en bucle
abierto para el sistema en bucle cerrado alcance
el límite de la estabilidad
M f = 180 º +∠GBA ( jωc )
Im
−1
Mf
Re
GBA ( jωc )
ωc
GBA ( jω )
Regulación Automática
donde ωc t.q. GBA ( jωc ) = 1
−1
Basado en Criterio
de Nyquist reducido:
válido sólo si GBA(s)
no tiene polos en el
SPD abierto.
M.G. Ortega
Márgen de fase (Mf)
z
Definición:
M f = 180 º +∠GBA ( jωc ) donde ωc t.q. GBA ( jωc ) = 1
G BA ( jω ) dB
Im
−1
M f > 0º
Re
ωc
GBA ( jω )
−1
ωc
ω ( rad / s )
0 dB
∠GBA ( jω )
− 180 º
M f > 0º
ω ( rad / s )
ωc
GBC ( s ) ESTABLE
GBC(s) ESTABLE ⇔ Mf > 0º
Regulación Automática
M.G. Ortega
Márgen de fase (Mf)
z
Definición:
M f < 0º
ωc
−1
GBA ( jω )
M f = 180 º +∠GBA ( jωc ) donde ωc t.q. GBA ( jωc ) = 1
G BA ( jω ) dB
Im
Re
−1
0 dB
ωc
ω ( rad / s )
∠GBA ( jω )
− 180 º
ωc
ω ( rad / s )
M f < 0º
GBC ( s ) INESTABLE
GBC(s) ESTABLE ⇔ Mf > 0º
Regulación Automática
M.G. Ortega
Márgen de fase (Mf)
¿Cuál es el máximo retardo Lmax que se puede introducir
a un sistema en b.a. antes de que el b.c. se inestabilice?
G BA ( jω ) dB
Im
−1
Mf
Re
ωc
GBA ( jω )
Regulación Automática
M f > 0º
− 180 º
M f 180 º
ω ( rad / s )
ωc
GBA ( jω )e
ωc
ω ( rad / s )
0 dB
∠GBA ( jω )
−1
Lmax =
ωc
− Lmax s
Lmax ω c
180 º
π
π
M.G. Ortega
Márgenes de ganancia y de fase
z
Mg =
Definición:
1
GBA ( jω180) =
Mg
− 1 ω180
M f > 0º
1
donde ω180 t.q. ∠GBA ( jω180 ) = − 180 º
GBA ( jω180 )
M f = 180 º +∠GBA ( jωc ) donde ωc t.q. GBA ( jωc ) = 1
G BA ( jω ) dB
Im
M g < 0dB (< 1)
ω c ω180
0 dB
ω ( rad / s )
Re
∠GBA ( jω )
ωc
GBA ( jω )
−1
− 180 º
ω ( rad / s )
M f > 0º
ω c ω180
GBC(s) ESTABLE ⇔ Mf > 0º y/o Mg>1 (0dB)
Regulación Automática
M.G. Ortega
Márgenes de ganancia y de fase
z
Valores orientativos:
z
z
z
Mf > 30º (por robustez Mf>50º)
Mg > 2
No son equivalentes numéricamente:
z
Ejemplos:
z
z
Sistema de primer orden: Mg=∞ , Mf > 90º
Sistema de segundo orden: Mg=∞ , Mf > 0º
Regulación Automática
M.G. Ortega
Márgenes de ganancia y de fase
z
No siempre son buena medida de robustez:
1
Mg
−1
1
Mg
Im
ω 180
f
ωc
G BA ( j ω )
MUY ROBUSTO
Regulación Automática
ω 180
Re
M S−1
M S−1
M
−1
Re
Im
−1
M
f
ωc
−1
G BA ( j ω )
POCO ROBUSTO
M.G. Ortega
Márgenes de ganancia y de fase
z
Sistemas con más de una ωc:
ω c5
M
4
f
−1
M 3f
¿ Mf ?
Im
ω c4
Re
ω c3
ω c2
ω
1
c
−1
GBA ( jω )
Regulación Automática
M.G. Ortega
Márgenes de ganancia y de fase
z
Sistemas con más de una ω180: ¿ Mg ?
1
M g2
1
M g3
Im
1
ω180
−1
2
ω180
Re
3
ω180
GBA ( jω )
Regulación Automática
M.G. Ortega
Márgenes de ganancia y de fase
z
Herramienta informática:
Control Toolbox de Matlab
z
z
num= 1; den=conv([1 1 0],[0.1 1]);
Gba=tf(num,den);
G BA ( s ) =
z
z
1
s ( s + 1)(0.1s + 1)
margin(Gba);
sisotool(Gba);
Regulación Automática
M.G. Ortega
Resumen
9
9
Los márgenes de estabilidad relativa permiten
medir la proximidad de la inestabilidad en bucle
cerrado.
En este curso:
9 Margen de ganancia:
Mg =
9
1
donde ω180 t.q. ∠GBA ( jω180 ) = − 180 º
GBA ( jω180 )
Margen de fase:
M f = 180 º +∠GBA ( jωc ) donde ωc t.q. GBA ( jωc ) = 1
9
GBC(s) estable ⇔ Mf > 0º y/o Mg>1 (0dB)
9
Hay que tener cuidado de cómo se aplican.
Regulación Automática
M.G. Ortega