Una línea poligonal es una secuencia de ______

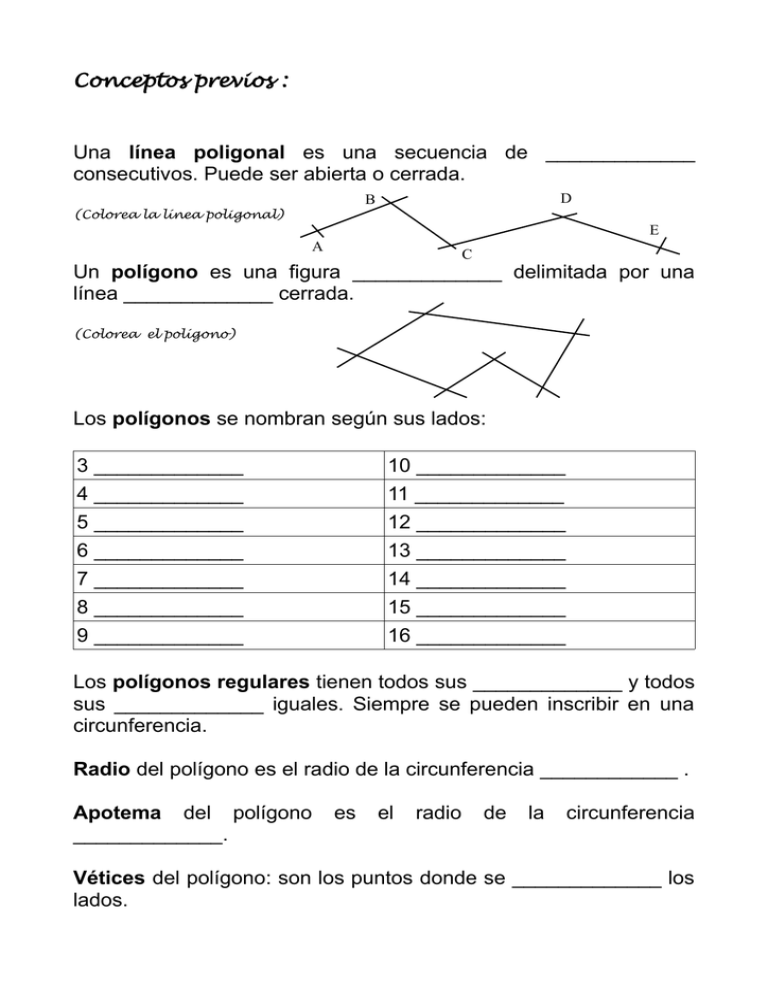
Conceptos previos :
Una línea poligonal es una secuencia de _____________
consecutivos. Puede ser abierta o cerrada.
D
B
(Colorea la línea poligonal)
E
A
C
Un polígono es una figura _____________ delimitada por una
línea _____________ cerrada.
(Colorea el polígono)
Los polígonos se nombran según sus lados:
3 _____________
4 _____________
5 _____________
6 _____________
7 _____________
8 _____________
9 _____________
10 _____________
11 _____________
12 _____________
13 _____________
14 _____________
15 _____________
16 _____________
Los polígonos regulares tienen todos sus _____________ y todos
sus _____________ iguales. Siempre se pueden inscribir en una
circunferencia.
Radio del polígono es el radio de la circunferencia ____________ .
Apotema del polígono
_____________.
es
el
radio
de
la
circunferencia
Vétices del polígono: son los puntos donde se _____________ los
lados.
El ángulo central de un polígono regular se calcula dividiendo 360º
entre el número de ____________ del polígono.
El ángulo interno de un polígono regular es el ángulo que forman
dos lados ____________. Es el ____________ del ángulo central.
•
Dibuja la circunferencia circunscrita
•
Calcula el ángulo central
•
Calcula el ángulo interno
Los polígonos
Dibuja el triángulo equilátero dado el lado.
A
•
Calcula el ángulo central
•
Calcula el ángulo interno
B
Dibuja el triángulo equilátero dado el radio.
A
B
Dibuja el cuadrado el lado.
A
•
Calcula el ángulo central
•
Calcula el ángulo interno
B
Dibuja el cuadrado dado el radio.
A
B
Los polígonos estrellados
Si a partir de un polígono regular de n lados se une un determinado
vértice con otro no _____________ de orden q ("avanzando" q
vértices) y se continúa el proceso del mismo modo hasta alcanzar
el vértice inicial, se obtiene un polígono regular estrellado, cuyos
lados y ángulos son todos iguales. La figura que se obtiene puede
representarse mediante la expresión n/q, siendo q el número de
vértices contados a partir del primero.
Para generar un polígono estrellado, la fracción n/q debe ser
irreducible, esto es, n y q han de ser primos relativos.
Dibuja un dodecágono regular inscrito en una circunferencia de
radio 60mm. Dibuja en colores diferentes los dodecágonos
estrellados posibles.
¿Sabrías calcular cuántos octógonos estrellados son posibles sin
dibujarlos?
¿Qué figura obtendrías uniendo todos los puntos pares y todos los
puntos impares de un octógono regular (orden 2)?