Capitulo 3 Calculo de estructuras metalicas
Anuncio

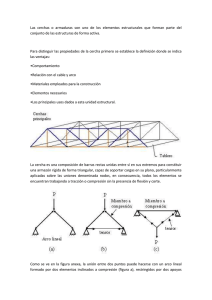
Diseño y cálculo del bastidor de un vehículo cosechador de fresas 3 Cálculo de estructuras metálicas . En este capítulo vamos a estudiar las bases de cálculo que hemos adoptado para el diseño y construcción del bastidor. Más adelante adaptaremos estos criterios a las necesidades especiales que requiere nuestro proyecto. 3.1. Estados límite La mayoría de las normas para el cálculo de estructuras metálicas se basan en la actualidad en el cálculo en los estados límites. Los estados límites son aquellos a partir de los cuales la estructura no cumple los requisitos de comportamiento del proyecto. Las condiciones de estado límite se clasifican en: • • Estado límite último. Estado límite de utilización o servicio. Los estados límites últimos son aquellos asociados a la rotura de una estructura o a otros tipos de fallo, que ponen en peligro la seguridad de las personas. Para simplificar, los estados previos al colapso estructural se clasifican y tratan como estados límites últimos en vez del propio colapso. Los estados límites últimos que deben tenerse en cuenta son los siguientes: - Pérdida del equilibrio de una estructura o parte de ella, considerada como cuerpo rígido. - Pérdida de capacidad de soporte de carga como, por ejemplo: rotura, inestabilidad, fatiga u otros estados límites tales como excesivas deformaciones y tensiones. Los estados límites de servicio corresponden a estados a partir de los que no se cumplen los criterios de utilización especificados. Son los siguientes: - Deformaciones o flechas que afectan al aspecto o al uso efectivo de la estructura (incluyendo el mal funcionamiento de máquinas y servicios) o causan daño a los remates o elementos no estructurales. - Vibración que causa incomodidad a las personas, daños al edificio o sus contenidos, o que limita su efectividad funcional. Memoria 18 Diseño y cálculo del bastidor de un vehículo cosechador de fresas 3.1.1. Cálculo en los estados límites Según el Eurocódigo 3, al considerar un estado límite, se verificará que: �(𝛾𝑓 ∙ 𝐹) ≤ donde: 𝑅 𝛾𝑀 𝛾𝑓 = Coeficiente parcial de seguridad para la acción F. 𝛾𝑀 = Coeficiente parcial de seguridad para la resistencia R. F= Valor de una acción. R= Valor de una resistencia para un estado límite relevante. A 𝛾𝑓 ∙ 𝐹 = 𝐹𝑑 se la denomina carga de cálculo mientras que a denomina resistencia de cálculo. 𝑅 𝛾𝑀 = 𝑅𝑑 se la 3.2. Análisis estructural El análisis estructural consiste en la determinación del efecto de las acciones sobre la totalidad o parte de la estructura, con objeto de efectuar las comprobaciones de los estados límites últimos y de servicio. El análisis estructural proporciona resultados a nivel global (reacciones, desplazamientos) y a nivel seccional (esfuerzos, curvaturas, elongaciones). Debe servir, también, para determinar el comportamiento a nivel local (tensiones, deformaciones) de aquellas zonas singulares en las que las hipótesis clásicas de la resistencia de materiales no sean aplicables: zonas locales próximas a cargas concentradas, nudos, cambios bruscos de sección, etc. En elementos unidimensionales, las constantes estáticas a considerar son el área, los momentos de inercia respecto de ejes principales y el módulo de torsión uniforme. El área de cortante y los efectos de distorsión de la sección y de la torsión de alabeo sólo necesitan tenerse en cuenta en algunos casos especiales. Los efectos del arrastre por cortante y de la abolladura de paneles comprimidos de chapa, sobre la rigidez de los elementos deben considerarse cuando afecten significativamente a los resultados del análisis estructural. Memoria 19 Diseño y cálculo del bastidor de un vehículo cosechador de fresas 3.2.1. Métodos de análisis Las condiciones que, en principio, debe satisfacer todo análisis estructural son las de equilibrio y las de compatibilidad, teniendo en cuenta las leyes de comportamiento de los materiales. Los métodos para el análisis global de una estructura se clasifican en: a) Análisis lineales, basados en las hipótesis de comportamiento elástico-lineal de los materiales constitutivos y en la consideración del equilibrio en la estructura sin deformar (análisis en primer orden). b) Análisis no lineales, que tienen en cuenta la no linealidad mecánica, esto es, el comportamiento no lineal de los materiales, y la no linealidad geométrica, es decir, la consideración de las condiciones de equilibrio sobre la estructura deformada (análisis en segundo orden). Los efectos de segundo orden, debidos a la deformación de la geometría de la estructura, deben tenerse en cuenta si aumentan significativamente los efectos de las acciones (esfuerzos y deformaciones) en la respuesta estructural. Para su evaluación se han de considerar las imperfecciones geométricas y mecánicas. 3.2.2. Clasificación de las secciones transversales Pueden utilizarse diferentes modelos para el análisis de estructuras de acero y para el cálculo de los esfuerzos resultantes (fuerza normal, esfuerzo cortante y momento flector y torsor en las barras de una estructura). Para el cálculo en los estados límites últimos, el proyectista se encuentra ante tres métodos de cálculo (Fig. 4.1). Las secciones transversales clases 3 y 4 con el procedimiento 'elástico-elástico" se diferencian solamente en que se requiere comprobación del pandeo para el tipo 4. Procedimiento "plástico-plástico" Sección transversal clase 1 Este procedimiento trata del cálculo plástico y de la formación de rótulas plásticas y redistribución de momentos en la estructura. Se desarrolla plasticidad total en la sección transversal (bloques de tensiones bi-rectangulares). La sección transversal puede formar una rótula plástica con la capacidad de rotación que se requiere para el análisis plástico. El estado límite último se alcanza cuando el número de rótulas plásticas es el suficiente para producir un mecanismo. El sistema debe permanecer en equilibrio estático. Memoria 20 Diseño y cálculo del bastidor de un vehículo cosechador de fresas Procedimiento "elástico-plástico" Sección transversal clase 2 En este procedimiento los esfuerzos se determinan siguiendo un análisis elástico y se comparan con las capacidades de resistencia plástica de las secciones transversales de los elementos. Las secciones transversales pueden desarrollar su resistencia plástica pero tienen una capacidad de rotación limitada. El estado límite último se alcanza mediante la formación de la primera rótula plástica. Procedimiento "elástico-elástico" Sección transversal clase 3 Este procedimiento consiste en el cálculo elástico puro de los esfuerzos y las capacidades de resistencia de las secciones transversales del elemento. El estado límite último se alcanza al fluir las fibras extremas de una sección transversal. La tensión calculada en la fibra más comprimida de la sección transversal del elemento puede alcanzar su límite elástico, pero el pandeo local tiende a impedir el desarrollo de la resistencia del momento plástico. Procedimiento "elástico-elástico" Sección transversal clase 4 La sección transversal se compone de paredes más delgadas que las de la clase 3. Es necesario tener en cuenta explícitamente los efectos del pandeo local (abolladura) cuando se determina el momento último o la capacidad de resistencia a compresión de la sección transversal. La aplicación de los tres primeros procedimientos anteriormente mencionados se basa en la suposición de que las secciones transversales o sus componentes no pandean localmente antes de alcanzar sus cargas límite últimas, esto significa que las secciones transversales no deben ser de pared delgada. Con el fin de cumplir dicha condición, las relaciones de esbeltez no deben exceder determinados valores máximos (Fig. 4.2). Una sección transversal debe clasificarse de acuerdo a la clase menos favorable (la más alta) de los elementos sometidos a compresión y/o flexión. Memoria 21 Diseño y cálculo del bastidor de un vehículo cosechador de fresas Fig. 3.1 Clasificación de secciones transversales y métodos de cálculo Memoria 22 Diseño y cálculo del bastidor de un vehículo cosechador de fresas Fig. 3.2 Esbelteces máximas para paneles comprimidos interiores (alas y almas) *) Ψ ≤ -1 se aplica cuando la deformación en la fibra comprimida es menor que la deformación en la fibra traccionada, tanto si la tensión de compresión es menor que fy como si la zona traccionada está plastificada. En este segundo caso, ψ es la relación algebraica entre la deformación plástica en la fibra traccionada (> fy/E) y la deformación elástica en la fibra comprimida (<fy/E). Memoria 23 Diseño y cálculo del bastidor de un vehículo cosechador de fresas 3.2.3. Elementos en compresión axial Como ya justificaremos más adelante vamos centrarnos en el estudio de perfiles tubulares de sección cuadrada y rectangular, puesto que son los perfiles que usaremos para nuestro bastidor. Vamos a tratar ahora el pandeo de elementos comprimidos de perfiles tubulares pertenecientes a las clases 1, 2 y 3 de sección transversal. Actualmente, el cálculo a pandeo de un elemento de acero sometido a compresión se realiza en la mayoría de los países europeos, utilizando las llamadas "curvas de pandeo europeas". Estas se basan en amplias investigaciones, tanto experimentales como teóricas, que tienen en cuenta especialmente las imperfecciones mecánicas (por ejemplo, tensión residual, distribución del límite elástico) y geométricas (por ejemplo, la desviación lineal) existentes en las barras. Fig. 3.3 Curvas de pandeo europeas En la actualidad, existen un gran número de códigos de cálculo y los procedimientos recomendados son a menudo muy similares, por lo que nos referiremos a Eurocódigo 3. Para los perfiles tubulares, el único modo de pandeo a tomar en consideración es el pandeo por flexión. No hace falta tener en cuenta el pandeo lateral con torsión ya que la rigidez torsional muy grande de una sección tubular impide cualquier pandeo con torsión. Memoria 24 Diseño y cálculo del bastidor de un vehículo cosechador de fresas La carga de cálculo a pandeo de un elemento a compresión se da por la siguiente condición: 𝑁𝑑 ≤ 𝑁𝑏,𝑅𝑑 donde: 𝑁𝑑 = Carga de cálculo del elemento comprimido. 𝑁𝑏,𝑅𝑑 = Resistencia de cálculo a pandeo del elemento. 𝑁𝑏,𝑅𝑑 = 𝑥 ∙ 𝐴 ∙ 𝑓𝑦 𝛾𝑀 donde: 𝐴 = es el área de la sección transversal; 𝑥 = es el factor de reducción de la curva de pandeo apropiada (Fig. 4.3), dependiente de la esbeltez adimensional 𝜆̅; 𝑓𝑦 = es el límite elástico del material utilizado; 𝛾𝑀 = es el coeficiente parcial de seguridad respecto a la resistencia. El factor de reducción 𝑥 es la relación entre la resistencia de pandeo 𝑁𝑏,𝑅𝑑 y la resistencia plástica axial 𝑁𝑃𝑙,𝑅𝑑 : 𝑥= 𝑓𝑏,𝑅𝑑 = tensión de pandeo de cálculo = 𝑓𝑦,𝑑 = límite elástico de cálculo = 𝑓𝑦 𝑁𝑏,𝑅𝑑 𝑓𝑏,𝑅𝑑 = 𝑁𝑃𝑙,𝑅𝑑 𝑓𝑦,𝑑 𝑁𝑏,𝑅𝑑 𝐴 𝛾𝑀 Memoria 25 Diseño y cálculo del bastidor de un vehículo cosechador de fresas La esbeltez adimensional 𝜆̅ se determina por: 𝜆̅ = 𝜆 𝜆𝐸 con 𝜆= 𝑙𝑏 𝑖 (𝑙𝑏 = longitud efectiva de pandeo; 𝑖 = radio de giro) 𝜆𝐸 = 𝜋 ∙ � 𝐸 𝑓𝑦 (esbeltez de Euler) La selección de la curva de pandeo (de la "a" a la "c" en la figura 4.3) depende del tipo de sección transversal. Se basa principalmente en los diferentes niveles de tensiones residuales que se originan a causa de los diferentes procesos de fabricación. Fig. 3.4 Curvas de pandeo según el proceso de fabricación Con fyb = Límite elástico del material básico (sin conformar en frío); fya = Límite elástico del material después de conformado en frío. Memoria 26 Diseño y cálculo del bastidor de un vehículo cosechador de fresas 3.2.4. Elementos en compresión y flexión combinadas Comprobación de la estabilidad Los elementos estructurales a menudo soportan simultáneamente cargas de compresión axial y momentos flectores. Según el Eurocódigo 3 la comprobación de la estabilidad se basa en las siguientes fórmulas de interacción lineal: 𝑀𝑦,𝑆𝑑 𝑁𝑆𝑑 𝑀𝑧,𝑆𝑑 + 𝜅𝑦 + 𝜅𝑧 ≤1 𝑁𝑏,𝑅𝑑 𝑀𝑦,𝑅𝑑 𝑀𝑧,𝑅𝑑 donde: 𝑁𝑆𝑑 = Valor de cálculo de la compresión axial (𝛾𝑓 veces la carga) 𝑁𝑏,𝑅𝑑 = 𝑥 ∙ 𝐴 ∙ 𝑥 𝑓𝑦 𝛾𝑀 = Factor de reducción (el más pequeño de y 𝑥𝑧 ) 𝐴 = Área de la sección transversal 𝑓𝑦 = Límite elástico 𝛾𝑀 = Coeficiente parcial de seguridad respecto a la resistencia 𝑀𝑦,𝑆𝑑 , 𝑀𝑧,𝑆𝑑 = Valor de cálculo del máximo absoluto del momento flector alrededor del eje 𝑦 o el 𝑧 según la teoría de primer orden. El incremento de los momentos flectores según la teoría de segundo orden se considera determinado 𝜆̅𝑦 y 𝜆̅𝑧 por medio de las longitudes de pandeo del sistema estructural completo. 𝑓𝑦 𝑀𝑦,𝑅𝑑 = 𝑊𝑒𝑙,𝑦 𝛾𝑀 y 2) 𝛾𝑀 𝑀𝑦,𝑅𝑑 = 𝑊𝑝𝑙,𝑦 𝑓𝑦 𝑓𝑦 𝑀𝑧,𝑅𝑑 = 𝑊𝑒𝑙,𝑧 𝛾𝑀 y 2) 𝛾𝑀 𝑀𝑧,𝑅𝑑 = 𝑊𝑝𝑙,𝑧 𝑓𝑦 para comportamiento elástico de una sección transversal (clase 3) para comportamiento plástico de una sección transversal (clases 1 para comportamiento elástico de una sección transversal (clase 3) para comportamiento plástico de una sección transversal (clases 1 Memoria 27 Diseño y cálculo del bastidor de un vehículo cosechador de fresas 𝜅𝑦 = 1 − 𝑁𝑆𝑑 𝑥𝑦 ∙ 𝑁𝑃𝑙 ∙ 𝜇𝑦 con 𝜅𝑦 ≤ 1,5 𝑊𝑒𝑙,𝑦 𝜇𝑦 = 𝜆�𝑦 �2𝛽𝑀,𝑦 − 4� + � − 1� con 𝜇𝑦 ≤ 0,9 𝜅𝑧 = 1 − 𝑁𝑆𝑑 𝑥𝑧 ∙ 𝑁𝑃𝑙 ∙ 𝜇𝑧 𝑊𝑝𝑙,𝑦 con 𝜅𝑧 ≤ 1,5 𝑊 𝜇𝑧 = 𝜆̅𝑧 �2𝛽𝑀,𝑧 − 4� + � 𝑒𝑙,𝑧 − 1� con 𝜇𝑧 ≤ 0,9 𝑊𝑝𝑙,𝑧 Para las secciones elásticas (clase 3) el valor 𝑊𝑒𝑙,𝑧 𝑊𝑝𝑙,𝑧 se considera igual a 1. 𝛽𝑀,𝑦 y 𝛽𝑀,𝑧 son los factores de momento uniforme equivalente para determinar la forma de distribución del momento flector 𝑀𝑦 y 𝑀𝑧 . Fig 3.5 Factor 𝛽𝑀 de momento uniforme equivalente Memoria 28 Diseño y cálculo del bastidor de un vehículo cosechador de fresas Calculo basado en tensiones Un elemento comprimido debe calcularse en base a la estabilidad y a la sección transversal que más tensión soporta. Han de considerarse simultáneamente la fuerza axial, los momentos flectores My y Mz y el esfuerzo cortante. Según el Eurocódigo 3, puede omitirse el esfuerzo cortante VSd cuando se cumple la siguiente condición: 𝑉𝑆𝑑 ≤ 0,5 𝑉𝑝𝑙,𝑅𝑑 donde 𝑉𝑝𝑙,𝑅𝑑 = Resistencia de cálculo plástico a esfuerzo cortante de una sección transversal Para perfiles tubulares rectangulares (RHS) toma la forma: 𝑉𝑝𝑙,𝑅𝑑 = 2𝑡 ∙ ℎ𝑚 ∙ 𝑓𝑦 √3 ∙ 𝛾𝑀 La ecuación 𝑉𝑆𝑑 ≤ 0,5 𝑉𝑝𝑙,𝑅𝑑 , se satisface en casi todos los casos prácticos. Para el cálculo elástico (secciones clase 3), sin tener en cuenta el esfuerzo cortante, puede utilizarse la siguiente ecuación: 𝑀𝑦,𝑆𝑑 𝑁𝑆𝑑 𝑀𝑧,𝑆𝑑 + + ≤1 𝐴 ∙ 𝑓𝑦𝑑 𝑊𝑒𝑙,𝑦 ∙ 𝑓𝑦𝑑 𝑊𝑒𝑙,𝑧 ∙ 𝑓𝑦𝑑 donde 𝑓𝑦𝑑 = 𝑓𝑦 𝛾𝑀 Esta ecuación puede usarse también como un límite inferior para el cálculo plástico de tensiones de secciones transversales de clases 1 y 2. Memoria 29 Diseño y cálculo del bastidor de un vehículo cosechador de fresas 3.3. Uniones soldadas en estructuras planas Las normas de cálculo expuestas en este apartado son aplicables para perfiles tubulares que tengan un límite elástico nominal inferior a 355 N/mm2 y una relación entre el límite elástico nominal y la resistencia última de (fy / fu) ≤ 0,8. Estas normas se limitan a las uniones sometidas a cargas predominantemente estáticas, siendo preciso usar métodos de cálculo alternativos bajo condiciones diferentes de carga. Todas las formulas de cálculo de uniones se dan en términos de resistencia en los estados límite, lo que significa que el efecto de las cargas de cálculo (las cargas características multiplicadas por los coeficientes parciales de seguridad apropiados), no debería sobrepasar la resistencia de cálculo de la unión. Las expresiones de resistencia de cálculo de la unión, que expondremos más adelante, incluyen ya un coeficiente de seguridad parcial para el material y unión (𝛾𝑀 ) o bien un coeficiente de resistencia de la unión (𝜙). 3.3.1. Clasificación de las uniones La clasificación de los nudos básicos que pueden aparecer en una estructura construida con perfiles tubulares, tales como en T (que incluye Y), X o K (que incluye N) no se basa, únicamente, en el aspecto físico del nudo, sino también, y fundamentalmente, en el método de transferencia de los esfuerzos en la unión. Fig. 3.6 Configuraciones básicas de los nudos: nudos en T, X y K Memoria 30 Diseño y cálculo del bastidor de un vehículo cosechador de fresas Fig. 3.7 Clasificación de los nudos (a) Cuando la componente normal del esfuerzo en una barra auxiliar se equilibra con el esfuerzo cortante (y la flexión) de la barra principal (a la que llamaremos cordón), el nudo se clasifica como nudo en T si la barra auxiliar es perpendicular al cordón y como nudo en Y en caso contrario. (b) Cuando la componente normal del esfuerzo en una barra auxiliar se equilibra, al menos en gran medida (diferencias menores del 20%), con la componente normal del esfuerzo en otra (u otras) barra auxiliar, situada en el mismo lado de la unión, el nudo se clasifica como nudo en K. La separación (espaciamiento “g”), se mide entre las barras auxiliares cuyas cargas se equilibran. Los nudos en N pueden considerarse como un tipo especial de nudo en K. (c) Cuando la componente normal del esfuerzo se transmite a través del cordón y se equilibra con una (o varias) barra auxiliar situada en el lado opuesto de la unión, el nudo se clasifica como un nudo en X. (d) Cuando un nudo presenta barras auxiliares en más de un plano, el nudo se clasifica como un nudo espacial. Como veremos en el capítulo 4, dedicado a la geometría del bastidor, en nuestro proyecto tendremos básicamente dos tipos de uniones: uniones en T, uniones en X, y uniones en ángulo. Vamos a centrarnos en el estudio de estas uniones sometidas a momento flector cuando se construyen con perfiles tubulares rectangulares. Memoria 31 Diseño y cálculo del bastidor de un vehículo cosechador de fresas 3.3.2. Uniones entre perfiles RHS sometidos a momento flector Uniones Vierendeel Se componen de elementos de cordón unidos a montantes que están casi siempre a 900 de los cordones. El principio de cálculo habitual en las vigas Vierendeel ha sido asumir la rigidez total de los nudos, pero esto rara vez sucede con uniones Vierendeel entre perfiles RHS. A diferencia de las celosías tipo Warren o Pratt trianguladas, en las que las uniones se acercan a una condición de articulación en su estado límite último y provocan que las barras auxiliares estén solicitadas por fuerzas predominantemente axiales, las uniones Vierendeel tienen montantes sometidos a momentos flectores importantes, así como a esfuerzos axiales y esfuerzos cortantes. Fig. 3.8 Unión Vierendeel Tanto la resistencia como la rigidez a flexión de una unión no reforzada disminuye al aumentar la relación b0 / t0 de esbeltez del cordón, y al disminuir la relación b1 / b0 (ó β) entre la anchura del montante y la del cordón. Las uniones con β = 1,0 y un valor bajo b0 / t0 se acercan a la rigidez total, pero todas las otras uniones no reforzadas pueden clasificarse como semirrígidas. Vamos a considerar los posibles tipos de rotura para estas uniones que se muestran en la figura 4.9. Los tipos de rotura representados suponen que ni las soldaduras ni las barras en sí son críticas (por ejemplo, se impide el pandeo local del montante). Memoria 32 Diseño y cálculo del bastidor de un vehículo cosechador de fresas Fig. 3.9 Posibles tipos de roturas para uniones RHS solicitadas por momentos flectores en el plano (a) Fluencia de la cara de cordón (b) Fisuración en el montante (c) Pandeo local de las paredes laterales del cordón Para cada mecanismo de rotura, el momento soportado por la unión tiene una expresión diferente. Estas expresiones de cálculo para solicitación de momento en el plano y fuera de él, se resumen en la figura 4.10. A efectos de cálculo, puede obtenerse una valoración aproximada de la resistencia a momento de la unión como el menor de los valores M*ip conseguidos de las ecuaciones expresadas en la tabla 4.10. Puede verse que la capacidad que predice la ecuación 1 tiende hacia el infinito cuando β tiende hacia la unidad, y por ello, este tipo de rotura, que corresponde a un estado de plastificación completa de la unión y como consecuencia a altas deformaciones de la misma, no es crítica en la zona de valores altos de β. Esto justifica el límite β ≤ 0,85 impuesto a la ecuación 1 y, para valores altos de β, probablemente gobernará el criterio de rotura por pandeo local del alma, expresado por la ecuación 3. De estas expresiones para M*ip puede verse que las uniones Vierendeel de RHS no reforzadas y de anchura total (β = 1,0) son capaces de desarrollar la capacidad total de momento flector del montante, suponiendo que b0 / t0 es lo suficientemente bajo. Memoria 33 Diseño y cálculo del bastidor de un vehículo cosechador de fresas Fig 3.10 Resistencia de cálculo de uniones en T y X soldadas de perfiles tubulares rectangulares bajo momentos flectores en el plano y fuera del mismo Las expresiones anteriores para resistencia a momento están basadas en solicitación a momento flector solamente, mientras que en vigas Vierendeel pueden también existir cargas axiales significativas en los montantes. El efecto de la carga axial en la capacidad a momento de la unión depende del tipo de rotura crítica, y por lo tanto se desarrolla un complejo conjunto de interacciones. Memoria 34 Diseño y cálculo del bastidor de un vehículo cosechador de fresas Se propone, de forma conservadora, utilizar una relación de interacción lineal para reducir la capacidad resistente a momento flector en el plano de unión Vierendeel, tal y como sigue: 𝑀𝑖𝑝 𝑁1 ∗+ ∗ ≤1 𝑁1 𝑀𝑖𝑝 Mip y N1 son el momento flector aplicado y la carga axial respectivamente en el montante, M*ip es el menor de los valores obtenidos de las ecuaciones 1, 2 y 3 (Fig. 4.10), y N*1 es la resistencia de la unión con una carga axial aplicada al montante únicamente (Fig. 4.11). Fig.3.11 Resistencia de cálculo de uniones T y X soldadas entre perfiles tubulares rectangulares bajo cargas axiales Memoria 35 Diseño y cálculo del bastidor de un vehículo cosechador de fresas Por tanto las uniones de RHS no reforzadas con β ≈ 1 y determinados valores b0 / t0 y t0 / t1 podrían alcanzar la capacidad total de momento del montante, pero la resistencia a momento de la unión, M*ip, calculada debe reducirse para tener en cuenta la influencia de la carga axial en el montante. Las uniones así calculadas que desarrollan todavía una resistencia a momento flector que excede la capacidad de momento del montante, pueden considerarse como completamente rígidas en los análisis de la viga Vierendeel. Cualquier otra unión (que comprende la mayoría de las posibles combinaciones de unión) debería considerarse como semirrígida. Uniones en ángulo Para el cálculo de uniones en ángulo sometidas a flexión y carga axial se aplica un factor de reducción al límite elástico del material donde: 𝑀𝑖𝑝 𝑁𝑖 + ≤𝛼 𝑁𝑟𝑖 𝑀𝑟𝑖 Nri = la resistencia axial del elemento i, bien a compresión o a tracción tal y como sea aplicable Mri = resistencia a momento de la barra i. 𝛼 = factor de reducción de la tensión que puede tomarse como 1,0 para uniones a inglete con placas de refuerzo. Para nudos en inglete sin placas de refuerzo, 𝛼 es una función de las dimensiones de sección transversal, figura 4.12. Para uniones sin placas de refuerzo, Ni tampoco debería exceder de 0,1 Nri. Fig. 3.12 Factores a de reducción de la tensión, para RHS sometidos a flexión alrededor del eje principal en uniones de ángulo recto a inglete sin refuerzo Memoria 36 Diseño y cálculo del bastidor de un vehículo cosechador de fresas 3.4. Uniones soldadas en varios planos Para uniones en XX y en TT a 90º, se ha demostrado de manera teórica que existe muy poca diferencia entre las resistencias de cálculo de uniones planas y multiplano. Sin embargo se recomienda aplicar un coeficiente de corrección de 0,9 a las resistencias de unión T y X planas para tener en cuenta las barras solicitadas fuera del plano. Fig. 3.13 Coeficientes de corrección de unión en varios planos 3.5 Cálculo de soldaduras Excepto para determinadas uniones en K y N con barras de relleno con recubrimiento parcial una unión soldada debería hacerse alrededor del perímetro completo de una barra de relleno por medio de una soldadura a tope, una soldadura en ángulo, o una combinación de ambas. Las soldaduras en ángulo para cualquier carga de la barra de relleno deberían calcularse para proporcionar una resistencia que no sea menor que la capacidad de dicha barra. Esto da como resultado el siguiente espesor de garganta mínima (a) para soldaduras en ángulo alrededor de las barras de relleno, asumiendo electrodos adecuados y los siguientes tipos de acero ISO [2]: a ≥ 0,95 t, para s 235 (fyi = 235 N/mm2) a ≥ 1,00 t, para s 275 (fyi = 275 N/mm2) a ≥ 1,07 t, para s 355 (fyi = 355 N/mm2) Si las soldaduras están dimensionadas en base a determinadas cargas de las barras de relleno, el calculista debe saber que la longitud total de la soldadura puede no ser eficaz, y el modelo para la resistencia de la soldadura debe justificarse en términos de resistencia y capacidad de deformación. Memoria 37 Diseño y cálculo del bastidor de un vehículo cosechador de fresas Longitud eficaz: (2 hi /sen θi) + bi para θi ≥ 60° Longitud eficaz: (2 hi /sen θi) + 2 bi para θi ≥ 50° Para 50° < θi < 60°, se sugiere una interpolación lineal. Fig. 3.14 Detalles de soldadura recomendados Por lo general, es más económico utilizar soldaduras en ángulo que soldaduras a tope. Sin embargo, el límite superior del tamaño de garganta o de los lados para soldaduras en ángulo dependerá del fabricante. La mayoría de las normas de soldadura solamente permiten soldadura en ángulo en el extremo de una barra de relleno si θi ≥ 60°. A causa de la dificultad de soldar en el talón de una barra de relleno con valores θi bajos, se ha establecido el límite inferior de θi = 30° para la aplicación de las reglas de cálculo de unión aquí presentadas. Algunos detalles de soldadura recomendados vienen ilustrados en la figura 3.14. Memoria 38