Desde la orilla de un río se observa la copa de un árbol, situado en

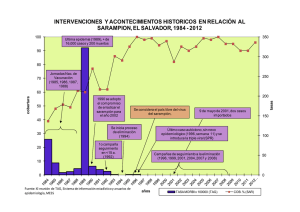
Desde la orilla de un río se observa la copa de un árbol, situado en la otra orilla, bajo un
ángulo de 60º. Si nos alejamos 8 m. de la orilla, el ángulo de observación es de 45º. Calcula
la altura del árbol y la anchura del río.
Tenemos que averiguar h (altura del árbol) y x
(anchura del río). Para ello utilizaremos la fórmula de
la tangente. Observa que los triángulos formados por
la copa del árbol, su base y los respectivos puntos de
observación son rectángulos y, por tanto, puedo
plantear:
tag 60 =
h
h
y de igual forma tag 45 =
x
x+8
(tangente es igual a cateto opuesto partido por cateto
contiguo)
Recordemos que tag 60 = 3
y que tag 45 = 1 .
Sustituyo el valor de la tag60 en la primera ecuación y despejo la h.
3=
h
⇔h=x 3.
x
Una vez que tengo el valor de h, lo sustituyo en la segunda ecuación así:
tag 45 = 1 =
x 3
⇔ ( x + 8) = x 3 .
x+8
(
Agrupo
la
x
y
saco
factor
común:
)
x 3 − x = 8 ⇔ x 3 − 1 = 8 y finalmente despejo x:
x=
8
= 10,93 m.
3 −1
Sustituyendo este valor en la expresión de h calculamos directamente la altura del árbol:
h = x 3 = 10,93 3 = 18,93 m.
Inicio del problema
L.Roche Ramón, 2006
Pág. 1 de 1