Ejemplo para transformar un DFA en una Expresión Regular

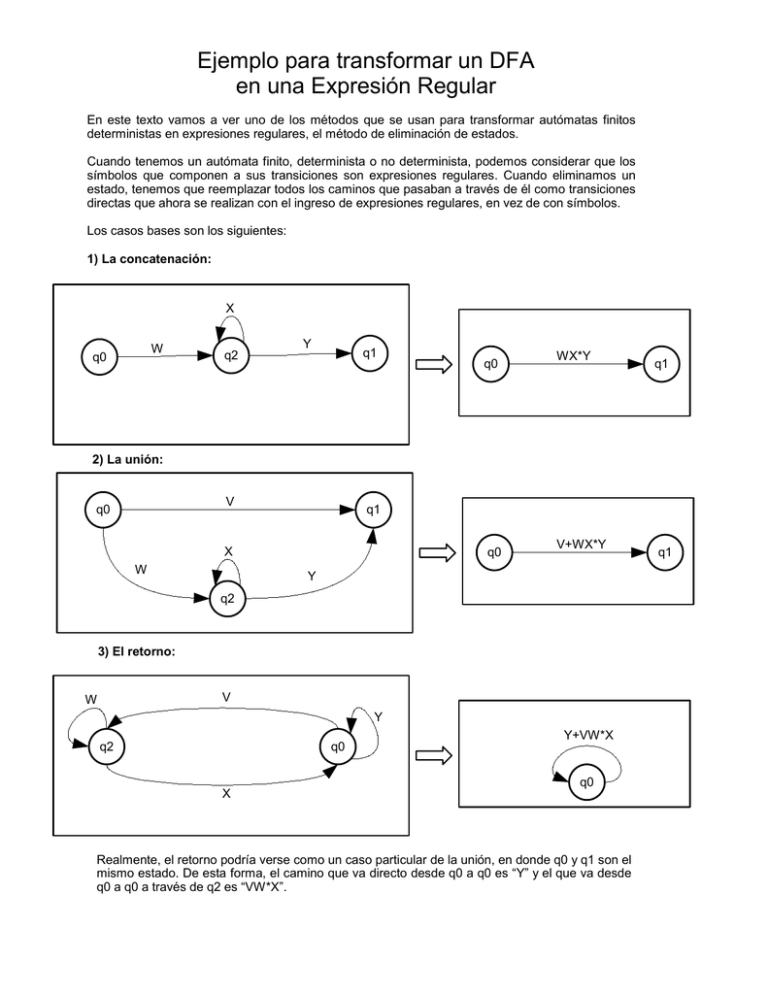
Ejemplo para transformar un DFA
en una Expresión Regular
En este texto vamos a ver uno de los métodos que se usan para transformar autómatas finitos
deterministas en expresiones regulares, el método de eliminación de estados.
Cuando tenemos un autómata finito, determinista o no determinista, podemos considerar que los
símbolos que componen a sus transiciones son expresiones regulares. Cuando eliminamos un
estado, tenemos que reemplazar todos los caminos que pasaban a través de él como transiciones
directas que ahora se realizan con el ingreso de expresiones regulares, en vez de con símbolos.
Los casos bases son los siguientes:
1) La concatenación:
X
W
q0
q2
Y
q1
q0
WX*Y
q1
2) La unión:
V
q0
q1
X
W
q0
V+WX*Y
Y
q2
3) El retorno:
V
W
Y
q2
q0
X
Y+VW*X
q0
Realmente, el retorno podría verse como un caso particular de la unión, en donde q0 y q1 son el
mismo estado. De esta forma, el camino que va directo desde q0 a q0 es “Y” y el que va desde
q0 a q0 a través de q2 es “VW*X”.
q1
Consejos finales antes de empezar con el ejemplo:
A la hora de reducir un autómata, se recomienda partir eliminando primero todos los estados que no
sean ni el de inicial ni los finales.
Cuando se eliminen todos estos estados y el autómata tenga más de un estado inicial, se deben hacer
tantas copias como estados de aceptación tenga el autómata. En cada una de las copias, se debe elegir
uno de los estados de aceptación diferentes. Todos los demás estados de aceptación de esta copia
pasarán a ser estados ordinarios. Ahora se deben reducir todos los autómatas copias a expresiones
regulares. La expresión regular final será la unión de todas las expresiones regulares resultantes de
cada una de las copias.
Al reducir por completo a un autómata finito se llegará a uno de dos casos:
1) El estado de aceptación es distinto al estado inicial
V
W
q0
Y
q1
X
En este caso, la expresión final de este autómata viene dada por (W + XY*V)*XY*
2) El estado de aceptación y el de inicio son el mismo
W
q0
En este caso, la expresión final de este autómata viene dada por W*
Supongamos que un autómata particular tuviese dos estados de aceptación y los autómatas copias que
terminaría reduciendo sean estos dos últimos que hemos mostrado hasta el momento. En este caso la
expresion regular total del autómata vendría dada por W* + (W+XY*V)*XY*
Ahora veamos un ejemplo más complejo para aplicar los conocimientos adquiridos. El autómata
de ejemplo es el siguiente:
q1
a,c
a
b
c
q0
c
q4
q3
a
b
a
q2
c
Lo primero que se debe hacer es transformar todas aquellas transiciones que contemplan más
de un símbolo en expresiones regulares del tipo “R+P”. En este caso, la única transición que
tenemos como objetivo es la de q0 a q1, que queda como “a+c”. Todas las demás permanecen
iguales, por ser símbolos.
a+c
q1
a
b
c
q0
c
q4
q3
a
b
a
q2
c
Ahora procedemos a eliminar el estado q2. Tenemos que fijarnos en todos los caminos que atraviezan a q2:
●q0 puede llegar a q3 pasando por q2.
●q1 puede llegar a q3 pasando por q2.
Veamos cómo quedan las transiciones del DFA cuando eliminamos q2:
1) Para llegar a q3, q0 primero debe pasar por q2 usando el símbolo “b”, luego puede pasar repetidas
veces por q2 (o ninguna vez) usando cero, uno o varios símbolos “c” y, por último, pasa de q2 a q3
con el símbolo “a”. Esto queda expresado con la expresión regular
T = bc*a
2) Para pasar de q1 a q3, primero debemos llegar a q2 con una “c”. Después de esto, podemos volver
repetidas veces a q2, usando el símbolo “c”. Podemos pasar cero, una o muchas veces por q2 de
esta forma. Ahora, como último paso, debemos llegar desde q2 a q3 con una “a”. Al concatenar estos
tres caminos obtenemos:
S = cc*a
cc*a=S
a+c=U
q1
a
b
q0
q3
bc*a=T
c
q4
a
Ahora, haciendo las simplificaciones correspondiente, sólo dejamos las expresiones regulares resumidas
por las letras mayúsculas (incluyendo a+c = U), y nos queda el autómata así:
S
U
q0
q1
T
a
b
q3
c
q4
a
Como siguiente paso, vamos a eliminar a q1. Las transiciones afectadas son:
1) De q0 a q3, que puede hacerlo a través de q1 o directamente, usando T. La expresión regular que
va de q0 a q3 a través de q1 es US y la expresión que va directamente de q0 a q3 es T. Como puede
ser una o la otra, como resultado queda la siguiente expresión:
V = T + US
2) De q3 a q3, a través de q1. Esto es: Primero llegamos a q1 con una “a”, y luego pasamos de q1 a
q3, usando S. La expresión resultante es:
W = aS
aS=W
q0
T+US=V
b
q3
c
q4
a
En el siguiente paso, eliminaremos q3. Las transiciones afectadas son:
1) De q0 a q4, pasando por q3: Primero vamos de q0 a q3 usando la expresión V. Luego vamos
de q3 a q3 repetidas veces, usando W. Por último, pasamos de q3 a q4 usando una “a”. La
expresión regular queda como sigue:
X = V.W*.a
2) De q4 a q4, pasando por q3 o directamente por q4 con una “c”. Para pasar a través de q3,
primero vamos de q4 a q3 con una “b”. Luego vamos de q3 a q3 usando W. Y, por último,
pasamos de q3 a q4 con una “a”. Como podemos ir desde q4 a q4 tanto usando la “c” como a
través de q3, la expresión regular que nos queda es:
Y = (c + bW*a)
q0
VW*a=X
q4
(c+bW*a) = Y
Si dejamos las Expresiones Regulares de forma
resumida, el último autómata nos queda así:
q0
X
q4
Y
Completemos las transiciones vacías (de q4 a q1 y de q1 a q1) con las
expresiones regulares vacías Z y P para obtener un autómata similar al que
aparece en la página 2:
Z=Ø
P=Ø
q0
q4
X
Y
De esta forma, podemos generar la expresión regular final a partir
de la fórmula (P + XY*Z)*XY* Esta expresión es equivalente a decir
que podemos ir de q0 una o muchas veces usando el camino corto
P o el largo XY*Z. Cuando ya nos decidimos de pasar de q0 a q4,
usamos X, y estando en q4 podemos hacer Y cero, una o varias
veces.
Expresión Final = (P + XY*Z)*XY* = (Ø* + XY*Ø)* XY* = (ε+Ø)*XY* = ε*XY* = XY*
Recordemos que las propiedades de las expresiones regulares nos dicen
que la clausura del conjunto vacío nos entrega al conjunto con el string
vacío:
Ø* = ε
Y que la concatenación con el espacio vacío nos produce al espacio
vacío (el operador nulo de la concatenación):
R.Ø = Ø
Ahora imaginemos que tenemos un autómata muy parecido al del ejemplo anterior, pero que
adicionalmente tiene al estado inicial q0 como estado de aceptación y también tiene un tercer estado final
más: q5.
a,c
a
q1
b
c
q0
c
q4
q3
a
b
d
a
q2
c
d
q5
La eliminación de los estados procedería de manera muy similar, hasta llegar al siguiente autómata de
expresiones regulares:
d
X
d
q0
q4
q5
Y
Ahora procedemos a hacer las tres copias correspondientes para este autómata:
X
d
q4
q0
q5
d
Y
q0
X
d
q4
q5
d
Y
d
q0
X
d
q4
q5
Y
Reduzcamos el primero de los tres autómatas:
X
d
q4
q0
q5
d
Y
Como se puede apreciar, ninguno de los estados q4 y q5 nos llevan a algún estado de aceptación, por lo
que se pueden eliminar sin tener problemas.
P=Ø
q0
En este caso, el autómata hacepta la expresión regular P* = Ø* = ε. Nótese que el lenguaje de este
autómata no es el conjunto vacío Ø, ya que el autómata es capaz de aceptar el string vacío ε.
Reduzcamos ahora el segundo autómata:
X
q0
d
q4
q5
d
Y
En este caso, el estado que no nos llevan a ningún estado de aceptación es el estado q5. Lo eliminamos:
q0
X
q4
Y
El autómata resultante es el mismo que el del ejemplo anterior, al igual que la expresión regular que
genera: XY*
Reduzcamos el último autómata:
d
X
q0
d
q4
q5
Y
Lo primero que hacemos es eliminar el estado q4, realizando una concatenación de expresiones
regulares:
XY*d = Z
q0
q5
d
Ahora obtenemos la expresión regular final del último autómata, la cual está dada por Zd*
Lo último que queda por hacer es unir las tres expresiones regulares de las tres copias del
autómata:
Expresión Final = ε + XY* + Zd*
DCC/2006.03.30