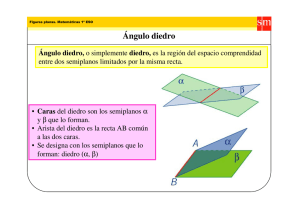
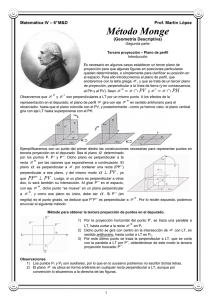
π π π

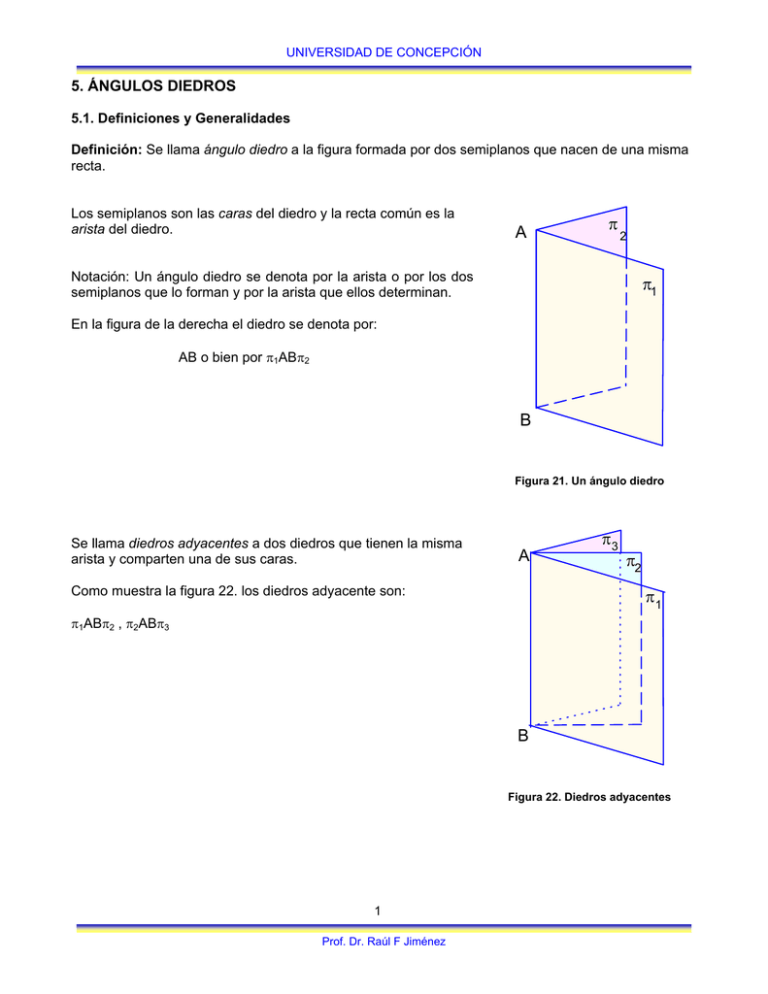
UNIVERSIDAD DE CONCEPCIÓN
5. ÁNGULOS DIEDROS
5.1. Definiciones y Generalidades
Definición: Se llama ángulo diedro a la figura formada por dos semiplanos que nacen de una misma
recta.
Los semiplanos son las caras del diedro y la recta común es la
arista del diedro.
A
π
2
2
Notación: Un ángulo diedro se denota por la arista o por los dos
semiplanos que lo forman y por la arista que ellos determinan.
π1
π
1
En la figura de la derecha el diedro se denota por:
AB o bien por π1ABπ2
B
Figura 21. Un ángulo diedro
Se llama diedros adyacentes a dos diedros que tienen la misma
arista y comparten una de sus caras.
A
π3
π2
π1
Como muestra la figura 22. los diedros adyacente son:
π1ABπ2 , π2ABπ3
B
Figura 22. Diedros adyacentes
1
Prof. Dr. Raúl F Jiménez
UNIVERSIDAD DE CONCEPCIÓN
Se llama diedros opuestos por la arista a dos diedros cuyas
caras son las prolongaciones de las caras del otro, como
muestra la figura 23.
π2
A
π
1
Dos diedros son iguales cuando son superponibles.
Se llama suma de dos diedros al diedro formado por las
dos caras no comunes de dos diedros adyacentes.
En la figura 22. el diedro π1ABπ3 es la suma de los diedros
π1ABπ2 y π2ABπ3.
El plano bisector de un diedro es el semiplano que pasando
por la arista divide al diedro en dos diedros iguales
B
Figura 23. Diedros opuestos por la arista
Definición: Se llama ángulo plano o ángulo rectilíneo de un
diedro al ángulo formado por dos rectas trazadas en cada
cara, perpendiculares a la arista y que tienen un punto en
común en la arista.
En la figura 24: en π1 trazamos la recta CD ⊥ AB y sobre el
plano π2, trazamos la recta EC ⊥ AB, siendo C el punto en
común. Entonces el ángulo rectilíneo del diedro π1ABπ2 es
el ECD.
A
π2
π1
E
C
D
E*
C*
Además, si elegimos un punto arbitrario C* sobre la arista y
levantamos las perpendiculares en ese punto C*, en ambos
planos, entonces
ECD =
E*C*D* (lados
respectivamente paralelos). Luego, para obtener el ángulo
rectilíneo de un diedro cualquiera es suficiente trazar por un
punto cualquiera de la arista un plano perpendicular a ella.
Las intersecciones de este plano con las caras del diedro
es el ángulo rectilíneo del diedro.
D*
B
Figura 24. Angulo rectilíneo de un diedro
Teorema 26: “Dos diedros iguales tienen ángulos rectilíneos iguales”
En efecto, consideremos dos diedros iguales, como muestra la figura 25, cuyos ángulos rectilíneos
son α y α*.
Haciendo coincidir los dos diedros de manera que los puntos C y C* coincidan, resulta que las rectas
CD y C*D* coinciden ya que están en un mismo plano y son ambas perpendiculares a AB en el
mismo punto. Esto mismo sucede con las rectas CE y C*E*.
Luego los ángulos α y α son iguales.
Teorema 27 (Recíproco del teorema 26) “Dos diedros que tienen ángulos rectilíneos iguales
son iguales”
2
Prof. Dr. Raúl F Jiménez
UNIVERSIDAD DE CONCEPCIÓN
π
π2
A
π 2∗
∗
A
2
2
π1
π
C
α
∗
1
E
∗
C
α∗
π 1∗
1
E
D
D∗
∗
B
B
Figura 25. Dos diedros iguales
5. 2. Medida de diedros
Los ángulos diedros se miden según la medida de los ángulos rectilíneos correspondientes. Luego, la
medida en grados, del diedro π1ABπ2 de la figura 25 es la medida en grados del ángulo α.
Definición: Un ángulo diedro se dice recto, agudo u obtuso según sea el ángulo rectilíneo recto,
agudo u obtuso.
Dos diedros serán complementarios de sus ángulos rectilíneos lo son, y serán suplementarios si sus
ángulos rectilíneos lo son.
El siguiente teorema se demuestra como se hace en Geometría Plana:
Teorema 28 “1. Dos diedros opuestos por su arista son iguales
2. Cuando dos diedros son opuestos por su arista, sus planos bisectores
coinciden.
3. Dos diedros adyacentes con caras exteriores en un mismo plano son
suplementarios y recíprocamente.
4. Dos diedros adyacentes y suplementarios tienen planos bisectores formando
un ángulo recto.
5. La suma de todos los diedros consecutivos que se pueden formar con una
arista común es igual a cuatro ángulos rectos.
6. El plano bisector de un diedro es el LG de todos los puntos equidistantes de
las caras del diedro.”
5. 3. Diedros orientados
Definición: Si en el espacio elegimos un sentido positivo para las rotaciones efectuadas alrededor de
una recta, diremos que el espacio está orientado.
3
Prof. Dr. Raúl F Jiménez
UNIVERSIDAD DE CONCEPCIÓN
Para indicar la orientación en el espacio trazamos una curva situada en
un plano perpendicular a la recta y trazamos una flecha para indicar el
sentido de la dirección.
En la figura de la derecha, hemos indicado el sentido positivo
convencional (conocido en Física como “regla de la mano derecha”).
El sentido positivo también se llama sentido directo.
Evidentemente, el sentido opuesto se llamar sentido negativo o
retrógrado.
Definición: Un diedro π1ABπ2 está orientado si se ha elegido un sentido positivo sobre su arista u un
sentido positivo
En la figura de la derecha mostramos dos
diedros orientados, en sentido positivo y
negativo.
A
π
2
π *
2
A*
π*
1
π
1
Note que π1ABπ2 y π2ABπ1 son diedros con
sentido opuestos, lo mismo que π1*A*B*π2*.
B*
B
positivo
negativo
6. PLANOS PERPENDICULARES
Definición: Dos planos son perpendiculares si forman un diedro recto.
Teorema 29. “Por una recta de un plano se puede trazar un único semiplano perpendicular a
este plano”.
La demostración es la misma de teorema análogo de la Geometría Plana o Planimetría
Teorema 30. “Si una recta es perpendicular a un plano, todo plano que contenga a esta recta,
es perpendicular al plano”.
H: l ⊥ π
π* contiene a l
T: π* ⊥ π
π∗ l
D: Sea P pie de l y π ∩ π* = l *.
Sea l 1 ⊥ l * en P.
l ⊥π⇒ l ⊥ l*
l 1 ⊥ l * ⇒ l P l 1 es ángulo rectilíneo del diedro π l *π* y
como l ⊥ l 1 , entonces el diedro es recto.
π
P
l*
l1
Figura 26. Planos perpendiculares
4
Prof. Dr. Raúl F Jiménez
UNIVERSIDAD DE CONCEPCIÓN
Teorema 31. (Primer recíproco del teorema 30) “Si dos planos son perpendiculares, entonces
toda recta traza en uno de ellos perpendicular a la intersección de los planos, será
perpendicular al otro plano”.
En efecto, observando la figura 26: supuesto π perpendicular a π* y si l 1 es perpendicular a l * en P,
entonces el ángulo formado por l y l 1 es el ángulo rectilíneo del diedro que es recto. Luego l es
perpendicular a l 1 y como también es perpendicular a l *, entonces l es perpendicular a π*.
AS: Formalice esta demostración.
Teorema 32 (Segundo recíproco del teorema 30) “Si dos plano son perpendiculares y si por un
punto cualquiera de uno de ellos se traza una recta perpendicular al otro plano, ésta recta está
totalmente contenida en el primer plano”.
AS: Redacte una demostración de este teorema, especificando hipótesis y tesis.
El teorema 30 y su primer recíproco, el teorema 31, se pueden enunciar de la siguiente manera:
“Para que dos planos sean perpendiculares es necesario y suficiente que uno de ellos
contenga una recta perpendicular al otro”.
AS: Especifique la condición necesaria y la condición suficiente.
Teorema 33. “Por una recta situada en un plano o fuera de él se puede trazar un único plano
perpendicular a ese plano”.
En efecto, supongamos que la recta l no está en el
plano π. Sea P un punto arbitrario de la recta y desde P
bajamos la perpendicular al plano π que lo atraviesa en
Q. Este plano interfecta a π según la recta l *. Las
rectas l y l * determinan un plano que es
perpendicular a π de acuerdo al teorema 30.
Pruebe Ud. la unicidad y el caso cuando la recta está
en el plano.
P
l
l*
Q
π
Teorema 34. La intersección de dos planos secantes y perpendiculares a un tercer plano, es
también perpendicular a este plano”.
H: π1 ∩ π2 = l
π1 ⊥ π
π2 ⊥ π
l
π2
A
π1
T: l ⊥ π
D: Sea A ∈ l arbitrario. Por A trazar recta perpendicular a π,
continúe Ud. con la demostración.
5
Prof. Dr. Raúl F Jiménez
P
π
UNIVERSIDAD DE CONCEPCIÓN
Corolario: “Todo plano perpendicular a la intersección de dos planos, es perpendicular a cada
uno de los planos”.
Teorema 35. “Si los lados de un ángulo son perpendiculares a las caras de un diedro,
entonces este ángulo y el ángulo rectilíneo del diedro son iguales o suplementarios”.
H: α = QPR, β = π1ABπ2
PQ ⊥ π1, PR ⊥ π2
A
T: α = β o bien α + β = 1800.
Q
π1
D: PQ ⊥ π1, y PR ⊥ π2 ⇒ Plano QPR ⊥ π1 y QPR ⊥ π2
S
β
π
R
α
2
P
∴ Plano QRP ⊥ AB
∴
B
QSR = β rectilíneo del diedro.
∴α y β tiene sus lados perpendiculares.
PROBLEMAS RESUELTOS:
1. Dado un diedro y una recta que encuentra su arista, hacer pasar por la recta un plano que corte las
dos caras del diedro de modo que la recta dada sea bisectriz del ángulo que se forma por las dos
rectas de intersección del plano pedido con los planos dados.
SOL:
Sea π1ABπ2 el diedro y l la
recta dados, La recta encuentra
la arista en P y sea Q un punto
de l . Por Q trazamos un plano
(verde) perpendicular a l , que
corta a π1 según l 1 y corta π2
según l 2, y ambas se cortan en
S con la arista AB. Por Q
trazamos QR // l 1. Sobre l 1,
ES = 2QR.
EQ (→)Q: F. El Plano (amarillo)
PEF es el plano pedido.
En efecto, QE=QF , PQ⊥EF,
luego ∆PEF isósceles y PQ
=bisectriz FPE
l
ππ22
F
A
l1
R
R
Q
Q
SS
P
E
E
B
l2
ππ11
EJERCICIOS:
1. Demuestre que todos los puntos M desde los cuales se dividen las distancias a las caras de un
diedro de modo que esos cuocientes son constantes, están en un mismo plano.
6
Prof. Dr. Raúl F Jiménez
UNIVERSIDAD DE CONCEPCIÓN
2. Determine los puntos del espacio que equidistan de las caras de un diedro y de dos rectas
paralelas.
3. Hallar el LG de los puntos M de un plano de donde se ve, bajo un ángulo recto, un trazo no situado
en el mismo plano..
4. Por los lados iguales de un triángulo isósceles se trazan los planos π1 y π2 perpendiculares al plano
del triángulo. Todo plano trazado por la base determina en los planos π1 y π2 los lados de un triángulo
isósceles que tienen la misma base que el triángulo primero. Hallar el LG de las intersecciones de las
transversales de gravedad y de los pies de las alturas.
5. Considere dos rectas l 1 y l 2 y un plano π perpendicular a l 1. Por las rectas se trazan dos planos
π1 y π2 rectangulares. Hallar el LG de los puntos comunes a los tres planos.
7. PROYECCION ORTOGONAL SOBRE UN PLANO
1, Proyección de una recta.
Definición: La proyección ortogonal de un punto sobre un plano es el pie de la perpendicular bajada
desde el punto al plano.
La perpendicular abatida se llama proyectante del punto.
La proyección ortogonal de una figura cualquiera sobre un plano es el conjunto de las proyecciones
de todos los puntos de la figura.
NOTA: Las proyecciones no ortogonales carecen de interés en este curso, por lo tanto desde ahora
hablamos de proyección en el entendido que se trata de proyecciones ortogonales.
Teorema 36. “La proyección de una recta sobre un plano es otra recta”.
Sea π el plano sobre el cual proyectamos la recta l . Sean A
y B dos puntos cualesquiera de l , cuyas proyecciones son
los puntos A´ y B´, respectivamente. La recta l y A´
determinan un plano π* perpendicular al plano π. La
intersección de los planos π y π* determinan la proyección
de la recta l , esto es, la recta l* .En efecto, si otro punto
cualquiera de l , digamos C se proyecta sobre π, la
perpendicular está completamente contenida en el plano π*
y encuentra a l * y su pie C´, será la proyección de C.
Como C es arbitrario, esto vale para todo punto de l
A
l
π
l*
A'
C
C'
B
π∗
B'
.
NOTA: El plano π se llama plano proyectante de l en el plano π. Si la recta l es paralela a π, ella será
paralela a su proyección. Si la recta l es perpendicular al plano π, su proyección es un punto.
Teorema 37. “Las proyecciones sobre un plano de dos rectas paralelas, son dos rectas
paralelas”.
7
Prof. Dr. Raúl F Jiménez
UNIVERSIDAD DE CONCEPCIÓN
En efecto, los planos proyectantes π1 y π2 determinan dos
parejas de rectas respectivamente paralelos: l *1 , l *2 y
AA´ , BB´. Luego, sus intersecciones l 1 y l 2 son el plano
π, también son paralelas.
l*1
A
π1
B
l*2
π2
l 1 A'
l 2 B'
π
2. Proyección de un ángulo recto.
Teorema 38. “Si uno de los lados de un ángulo recto es paralelo a un plano, entonces su
proyección sobre el plano, es un ángulo recto”.
En efecto, sea α el ángulo recto formado por las
rectas l 1 y l 2 con vértice en A. Sea l 2 // π y sea π*
el plano proyectante de l 2 que interfecta π según
l 2* y tal que Pr⎥πA = A´ .
Luego, l 2* ⊥ l 1
l 2* ⊥ AA´
∴ l 2* ⊥ plano (l 1, l 1*)
∴ l 2* ⊥ l 1*
l
2
π∗
π∗
l*l*22
ππ
8
Prof. Dr. Raúl F Jiménez
A
α
l
1
l*11
A'
A'
UNIVERSIDAD DE CONCEPCIÓN
Teorema
“Cuando dos, planos se cortan, la recta de uno de ellos que forma el mayor
ángulo con el otro plano es la perpendicular a su intersección”
En efecto:
Sea π1 ∩π2 = AB. Sea P ∈ π2 y PQ ⊥ AB.
Sea PR una recta cualquiera.
Sean Pr π1 PQ = P * Q , Pr π1 PR = P * R .
PP* ⊥ π1 y PQ ⊥ AB ⇒ P*Q ⊥ AB
∴P*Q < P*R
Sea P*R* = P*Q.
∴ ∆ PP*Q ≅ ∆ PP*R* ⇒ PQP* =
PR*P* =
exterior ∆ PR*R
Pero
PRR* +
RPR*
∴ PR*P* =
PQP* <
PRQ
∴
π2
P
π1
P*
R*
PR*P*.
A
R
Q
B
Perpendicular común a dos rectas.
Definición : Se llama recta perpendicular común a dos rectas dadas a la recta que encuentra ambas
rectas dadas y es perpendicular a cada una de ellas.
El siguiente teorema garantiza la existencia de esta perpendicular común.
Teorema
“Por dos rectas cualesquiera no situadas en un mismo plano se puede trazar una
única recta perpendicular a ambas”
9
Prof. Dr. Raúl F Jiménez
UNIVERSIDAD DE CONCEPCIÓN
Q
l1
π∗
l **
P
π
10
Prof. Dr. Raúl F Jiménez
l2