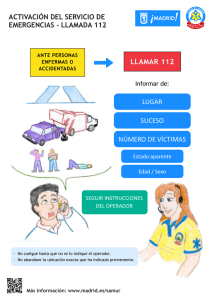
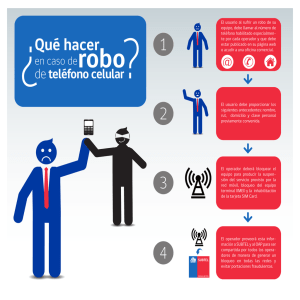
MÉTODOS MATEMÁTICOS TEMA 4: OPERADORES LINEALES

MÉTODOS MATEMÁTICOS
ESPACIOS DE HILBERT Y OPERADORES LINEALES
Profesora: Mª Cruz Boscá
TEMA 4: OPERADORES LINEALES
L1 ≡ ( L1 , ⋅ 1 )
Notación: sean
y
L2 ≡ ( L2 , ⋅ 2 ) dos
espacios normados; sea
T un
T : D(T1 ) < L1 → L 2 , de recorrido R(T ) < L2 ; sea L( L) el espacio lineal
constituido por todos los operadores T con dominio D (T ) = L y recorrido R (T ) < L , y sea
H un espacio de Hilbert.
Lema: ∀D | D = H se tiene x, y = 0 ∀y ∈ D ⇒ x = 0 .
operador lineal
Lema: Dado T ∈ L( L) , L pre-Hilbert, k = ℂ ⇒ ( T = 0 ⇔ x, Tx = 0 ∀x ∈ L ) .
Lema: Dados Ti ∈ L( L), i = 1, 2 , L pre-Hilbert, k = ℂ ⇒
T1 = T2 ⇔
x, T1 x = x, T2 x
∀x ∈ L .
Aplicaciones lineales entre espacios lineales
T con dominio D(T ) y recorrido R(T ) ,
T : D(T ) ⊂ L1 → R (T ) ⊂ L2 , es aplicación lineal u operador lineal del
espacio lineal L1 sobre el espacio lineal L2 , ambos sobre el cuerpo común
Λ , sii satisface:
a) D (T ) < L1
b) T es univaluada: ∀x ∈ D (T ) ∃! y ∈ R (T ) : T ( x ) = y (notación:
y = Tx ),
c) ∀x, y ∈ D (T ), ∀α , β ∈ Λ : T (α x + β y ) = α T ( x ) + β T ( y ) .
Una aplicación
Denominación: aplicación lineal
≡
operador lineal
≡
homomorfismo.
T con dominio D(T ) y recorrido R(T ) ,
T : D(T ) ⊂ L1 → R (T ) ⊂ L2 , es aplicación antilineal u operador antilineal del
espacio lineal L1 sobre el espacio lineal L2 , ambos sobre el cuerpo común
Λ = ℂ , sii satisface:
Una aplicación
D(T ) < L1
b) T es univaluada: ∀x ∈ D (T ) ∃! y ∈ R (T ) : T ( x ) = y (notación:
y = Tx ),
c) ∀x, y ∈ D (T ), ∀α , β ∈ Λ : T (α x + β y ) = α * T ( x ) + β * T ( y ) .
a)
© M.C. Boscá, U. de Granada
1
Propiedades:
Dada una aplicación lineal
T : D(T ) < L1 → R (T ) ⊂ L2 , se tiene:
R(T ) < L2
b) T (01 ) = 0 2 ( 0i es elemento neutro de la ley ( + ) en L i , i = 1, 2
c) T ( − x) = −T ( x) ∀x ∈ D (T )
d) kerT= x ∈ D (T ) : Tx = 0 2 < L1 (núcleo o kernel del operador)
a)
{
)
}
D ( T ) = L 1 y d i m L 1 es finita: dim D (T ) = dim ker T + dim R (T ) ,
denominándose nulidad de T a la dim kerT y rango de T a la dim R (T ) .
e) Si
Gráfico de un operador lineal
Dada una aplicación lineal T : D (T ) ⊂ L1 → R (T ) ⊂ L2 , se define su
gráfico Γ(T ) como
Γ(T ) = {( x1 , x2 ) ∈ L1 × L2 : x1 ∈ D(T ), x2 = Tx1 ∈ R(T )} ⊂ L1 × L2 .
Γ(T ) < L1 ⊕ L2
Teorema del gráfico: Un subespacio lineal Γ(T ) < L1 ⊕ L2 es gráfico
de algún operador lineal entre
es, si
Γ
corta al eje
L1
y
L2 ⇔
((01 , y ) ∈Γ ⇒ y = 02 )
(esto
L2 , lo hace sólo en el origen).
Igualdad entre operadores lineales: Dados dos operadores lineales
y T2 , son iguales
⇔ Γ(T1 ) = Γ(T2 ) ⇔ D(T1 ) = D(T2 ) = D(T ) y
T1
T1 x = T2 x ∀x ∈ D(T ) .
Extensiones y restricciones: Dados dos operadores lineales
D(T1 ) ⊂ D(T2 ) y T1 x = T2 x ∀x ∈ D(T1 ) , entonces T2
extensión de T1 a D(T2 ) , y T1 es una restricción de T2 a D(T1 ) .
tales que
T1
y
T2 ,
es una
Notación:
T2 ⊃ T1
T1 ⊂ T2
»»
T2
es una extensión de
T1 .
»»
T1
es una restricción de
T2 .
Operador lineal inverso
Dado un operador lineal T : D (T ) < L1 → R (T ) < L 2 la relación inversa T ( −1)
se define según:
T ( −1) : D (T ( −1) ) = R (T ) → R (T ( −1) ) = D(T ) tal que ∀y ∈ D (T −1 ) se tiene T ( −1) y = x
con x ∈ D (T ) y Tx = y .
© M.C. Boscá, U. de Granada
2
En general, T ( −1) no tiene por qué ser un operador (i.e.: no tiene por qué
ser univaluada).
Dado un operador lineal T : D (T ) < L1 → R (T ) < L 2 la relación inversa T ( −1)
es un operador lineal T −1 : D (T −1 ) = R (T ) < L2 → R (T −1 ) = D (T ) < L1 ⇔ T es un
operador inyectivo ⇔
ker T = {01} .
[ (Tx1 = Tx2 ) ⇒ x1 = x2 ] ⇔
[ Tx = 0 2 ⇒ x = 01 ], i.e.:
Dado un operador lineal T : D (T ) < L1 → R (T ) < L 2 , T
operador no singular ⇔ ∃T
−1
se define como
operador lineal.
Dado un operador lineal T : D (T ) < L1 → R (T ) < L 2 no singular ⇒
∃ T −1T ≡ I D : D (T ) → D (T ) / T −1Tx = x ∀x ∈ D (T )
∃ TT −1 ≡ I R : R (T ) → R (T ) / TT −1 y = y ∀y ∈ R (T )
Dado un operador lineal T : D (T ) < L → R (T ) < L , T
se define como
⇔ D (T ) = R (T ) = L y T es no singular ⇔
operadores lineales, y TT −1 = T −1T = I .
operador invertible
∃ T , T −1 ,
Dados dos operadores lineales Ti : D (Ti ) < L1 → R (Ti ) < L2 , i = 1, 2 , tales que
D (T1 ) ⊂ D (T2 ) y T2 ( x) = T1 ( x) ∀x ∈ D (T1 ) , se dice que T2 es una extensión de
T1 a D (T2 ) y que T1 es una restricción de T2 a D (T1 ) , simbolizándose T1 ⊃ T2 .
Operadores lineales acotados y continuos
Operador lineal continuo/acotado (∈ A )
Dados dos espacios normados L1 y L2 sobre el mismo cuerpo k , un
operador lineal A : D ( A) < L1 → R ( A) < L2 es continuo en x ∈ D ( A) ⇔
⇔ ∀ε > 0 ∃δ ( x, ε ) > 0 /
A( x) − A( y ) 2 < ε ∀y ∈ D( A) tal que x − y 1 < δ
⇔ ∀ { xn }n =1 ⊂ D( A) se tiene que xn → x ⇒ A( xn ) → A( x) .
∞
Un operador lineal A : D ( A) < L1 → L2 es continuo si lo es ∀x ∈ D ( A) .
Dados dos espacios normados L1 y L2 sobre el mismo cuerpo k , un
operador lineal A : D ( A) < L1 → R ( A) < L2 es acotado
⇔ ∃k ∈ ℝ finito, k ≥ 0 /
Ax 2 ≤ k x 1 ∀x ∈ D( A) .
-Nota: Obsérvese que K min = sup
x ≠0
Ax
2
x1
es el menor valor de k para el que se verifica
la anterior desigualdad para todo operador lineal acotado.
© M.C. Boscá, U. de Granada
3
Dados dos espacios normados L1 y L2 sobre el mismo cuerpo k , un
operador lineal T : D (T ) < L1 → R (T ) < L2 es continuo ⇔
⇔ es continuo en un punto de su dominio (cualquiera)
⇔ es continuo en x = 0
⇔ es acotado.
La suma, el producto por un escalar y la composición de operadores
lineales continuos dan como resultado otro operador lineal continuo.
Norma de un operador lineal acotado
Definición: Dados dos espacios normados L1 y L2 sobre el mismo cuerpo k
y un operador lineal acotado A : D ( A) < L1 → R ( A) < L2 , se define la norma
del operador, A ∈ ℝ,
A = sup
Ax
x 1 ≠0
x∈D ( A )
x1
Ax 2 ≤ A
2
A ≥ 0 , según
.
x 1 ∀x ∈ D( A) .
Teorema: Definiciones equivalentes para la norma de un operador (¡lineal
acotado!):
a) A = inf {k ∈ ℝ, k ≥ 0 / Ax 2 ≤ k x 1 ∀x ∈ D( A)}
b) sup Ax
0 < x 1 ≤1
2
c) sup
x∈D ( A )
x 1 ≤1
x∈D ( A ), x ≠0
Ax
x1
2
d) sup Ax
x 1 =1
2
.
x∈D ( A )
Propiedades
(A ( L1 , L2 ), ⋅ ) es un espacio lineal normado (cuerpo k ).
(A ( L1 , L2 ), ⋅ ) con L2 espacio de Banach es un espacio de Banach.
A ( L1 , L 2 ) = LC ( L1 , L2 ) ≠ L ( L1 , L2 ) .
A ( Ln , L) = LC ( Ln , L) = L ( Ln , L) .
En (A ( L1 , L2 ), ⋅ ) la suma (de elementos de A , esto es, de operadores lineales
acotados), el producto por un escalar y el producto de operadores son
también elementos del espacio (o sea, operadores lineales continuos).
-Por ejemplo: An → A, Bn → B, α n → α ⇒ An + Bn → A + B, α n An → α A, An Bn → AB .
Dados A1 ∈ A ( L1 , L2 ) y A2 ∈ A ( L2 , L3 ) , entonces Ain es acotado, Ain
≤
n
Ai ;
A2 A1 ∈ A ( L1 , L3 ) y A2 A1 ≤ A1 ⋅ A2 .
-Nota: la última propiedad permitirá que A ( H ) = A ( H , H ) , H ≡ espacio de Hilbert (y, por
tanto, espacio completo), constituya un álgebra de Banach.
© M.C. Boscá, U. de Granada
4
El espacio Banach A ( H ) ≡ A ( H , H ) con dim H > 1 no es espacio euclídeo
(i.e.: la norma no cumple la ley del paralelogramo, o sea, no deriva de un
producto escalar).
Teoremas del operador inverso acotado:
Dado un operador lineal T : D (T ) < L1 → R (T ) < L 2 , L2 ≠ {02 } , entonces
∃ T −1 operador lineal acotado ⇔ ∃ k > 0 : Tx 2 ≥ k x 1 ∀ x ∈ D(T ) .
Dado un operador lineal acotado biyectivo A : L1 → L 2 , con L1 y L 2
Banach, entonces ∃ A−1 y es operador lineal acotado.
Representación matricial:
Todo operador lineal acotado A ∈ A ( H ) con H espacio de Hilbert
separable, admite representación como una matriz cuadrada de elementos
Aij = ei , Ae j , siendo {ei }i∈I , card I ≤ ℵ0 , una base ortonormal numerable de
H y teniéndose ∀x ∈ H , x = ∑ α i ei , que
i∈I


Ax = ∑  ∑ Aijα j  ei ,
i∈I  j∈I

esto es,
( Ax )i = ∑ Aijα j .
j∈I
Operadores cerrados
Definiciones y teoremas
Un operador lineal T : D (T ) < L1 → L 2 se define como cerrado ⇔ su
gráfico η (T ) = {( x, y ) ∈ L1 × L2 : x ∈ D (T ), y = Tx} < L1 ⊕ L2 es cerrado (i.e.:
η (T ) = η (T ) ⊲ L1 ⊕ L2 ; recordar que L1 ⊕ L2 es el espacio suma directa externa
de L1 y L2 , donde se ha definido la norma ( x, y ) = x 1 + y 2 ; dado
S < L1 ⊕ L2 , S es gráfico de un operador lineal T : D(T ) < L1 → L 2 ⇔
( (0, y ) ∈ S ⇒ y = 0 ); además, si L1 y L2 son Banach, entonces L1 ⊕ L2 es
Banach).
Un operador T : D (T ) < L1 → L 2 es cerrado ⇔
(∀ { xn }n =1 ⊂ D(T ), xn → x, Txn → y ) ⇒ (x ∈ D(T ), y = Tx)
∞
Dado un operador lineal acotado A : D ( A) < L1 → L 2 , entonces ⇒
Si D ( A) = D ( A) , entonces A es cerrado, y
Si A es cerrado y L2 es Banach, entonces D ( A) = D ( A) .
Dado un operador lineal acotado A ∈ A ( D ( A), H ) , A es cerrado
⇔ D( A) = D( A) .
© M.C. Boscá, U. de Granada
5
Teorema del gráfico cerrado:
Dados dos espacios Banach L1 , L2 y un operador lineal T : D (T ) < L1 → L 2 ,
con D (T ) = D (T ) , entonces ⇒ ( T es operador cerrado ⇔ T es operador
acotado).
Un operador lineal
T : D(T ) < L1 → L 2
clausurable ⇔ posee extensión T
c
ext
(i.e.:
se define como cerrable o
⊇ T cerrada
∃ Textc : D(Textc ) < L1 → L2 : D(Textc ) ⊇ D(T ), Textc x = Tx ∀x ∈ D(T )
y
Textc
es
operador cerrado).
c
Si T es cerrado, es cerrable (e.g.: Text
=T).
T es cerrable ⇔ η (T ) no posee puntos (0, y ) con y ≠ 0 ⇔
[({ xn }n∈N ⊂ D(T ), xn → 0, Txn → y ) ⇒ y = 0] ⇔
 { xn }n∈N ⊂ D(T ), xn → x, {Txn } → z1 
⇔ 
 ⇒ z1 = z2 .
y
D
T
x
Ty
z
⊂
→
→
(
),
y
,
{
}
{
}
n
n
n
2
n∈N


Dado T operador cerrado o acotado, y no singular ⇒ T −1 es operador
cerrado.
Clausura de un operador
Dado un operador cerrado o cerrable T : D (T ) < L1 → L 2 , se define su
cierre o clausura T como su extensión cerrada minimal, i.e., la extensión
c
de él,
cerrada del mismo tal que, dada cualquier otra extensión cerrada Text
se tiene η (T ) ⊂ η (Textc ) .
Dado T operador cerrado ⇒ T = T .
Dado un operador lineal T : D (T ) < L1 → L 2 , operador no cerrado pero
clausurable, entonces ⇒
T posee clausura T ,
η (T ) = η (T ) ,
( )
D(T ) ⊂ D T ⊂ D(T ) .
Nota: Existen operadores lineales T : D(T ) < L1 → L 2 que son:
Cerrados pero no acotados (e.g.: el operador diferencial, ver Vera p. 192).
Acotados pero no cerrados (e.g.: el operador identidad I D , D L , ver Vera p. 192).
Ni cerrados ni acotados.
© M.C. Boscá, U. de Granada
6
Extensión de operadores lineales acotados
Teorema de extensión de un operador lineal acotado con recorrido en
un Banach:
Dado un operador lineal acotado A : D ( A) < L1 → L2 , con L2 espacio de
Banach, entonces ⇒ ∃! A ext : D ( Aext ) = D ( A) ⊲ L1 → L2 , operador lineal acotado
tal que:
Aext ⊃ A , i.e.: Aext x = Ax ∀x ∈ D( A) y η ( Aext ) ⊃ η ( A)
D( Aext ) = D( A)
∀ x ∈ D( A) : A ext x = lim Axn con { xn } ⊂ D( A) y xn → x
n →∞
Aext = A
y Aext = A .
Todo operador lineal acotado con dominio de definición denso en el
correspondiente espacio normado y recorrido en un Banach puede
extenderse a todo el espacio conservando su norma.
Dado A : D ( A) < H → H , operador lineal acotado con dominio y recorrido
sobre un Hilbert, entonces ⇒ existen unas extensiones acotadas A de A a
D( A) , A : D( A) = D( A) ⊲ H → H , única, y AH de A a todo el espacio,
AH : D( AH ) = H → H , no única en general, tales que:
A ⊃ A , i.e.: Ax = Ax ∀x ∈ D( A) ; η ( A) ⊃ η ( A) ; D( A) = D( A) ⊃ D( A) y
∀ x ∈ D( A) : Ax = lim Axn con { xn } ⊂ D( A) y xn → x .
n →∞
AH ⊃ A , i.e.: AH x = Ax ∀x ∈ D( A) ; η ( AH ) ⊃ η ( A) ; D( AH ) ⊃ D( A) y, puesto
(
que ∀x ∈ H : x = x1 + x2 con x1 ∈ D( A) , x2 ∈ D( A)
)
⊥
, entonces ∀x ∈ H \ D ( A) :
AH x = Ax1 + A⊥ x2 , siendo A⊥ ∈ A (( D( A))⊥ , H ) (i.e.: un operador lineal acotado con
(
)
⊥
dominio D( A⊥ ) = D( A) ).
AH ≥ A = A ( AH = A = A cuando A⊥ = 0 ).
Todo operador lineal acotado con dominio y recorrido en un Hilbert puede
extenderse a todo el espacio; por tanto, en el estudio de un operador
continuo A sobre un H puede suponerse siempre que el operador
A ∈ A ( H ) = A ( H , H ) (aunque su extensión, en general, no es única si D( A) ≠ H ).
© M.C. Boscá, U. de Granada
7
Teorema de representación de Riesz o de Riesz-Fréchet:
Dado
F ∈H
*
un
espacio
de
Hilbert
H , entonces un funcional lineal
⇔ ∃! g ∈ H / F ( x) = g , x ∀x ∈ H , teniéndose F = g ( g se denomina
el vector “generador” del funcional F , H * representa el espacio dual del H * , véase tema 5).
Adjunto de un operador
Dado un operador lineal acotado A ∈ A ( H ) se define su operador adjunto
A+ como el operador lineal A+ : H → H tal que A+ x, y = x, Ay
∀x, y ∈ H .
∀A ∈ A ( H ) ∃! A+ ∈ A ( H ) (demostración: requiere el teorema de Riesz).
El concepto de operador adjunto generaliza el de matriz adjunta, pues si,
como vimos, todo operador lineal acotado A ∈ A ( H ) , con H espacio de
Hilbert separable, admite representación como una matriz cuadrada de
elementos Aij = ei , Ae j , siendo {ei }i∈I , card I ≤ ℵ0 , una base ortonormal
numerable de H , entonces se tiene que la matriz asociada al operador
adjunto A+ es la transpuesta de la conjugada de la matriz de A :
A+ = ( A )* .
ij
ji
Propiedades: ∀A, An ∈ A ( H ) , se tiene
A ∈ A ( H ) ⇔ A+ ∈ A ( H ) .
A++ = A y A+ es cerrado.
A+ = A ; (α A)+ = α * A+ ∀α ∈ k .
( A1 + A2 )+ = A1+ + A2+ ; ( A1 A2 ) + = A2+ A1+ .
A+ = A ; A+ A = AA+ = A
2
.
Si A es invertible, A−1 ∈ A ( H ) ⇒ A+ invertible, ( A+ )−1 ∈ A ( H ) y
( A+ )−1 = ( A−1 )+ .
ker A+ = ( R ( A)) ⊥ y ker A = ( R ( A+ )) ⊥ ; H = R( A) ⊕ ker A+ .
Dado un
operador lineal T : D(T ) < H → H , se denomina operador
adjunto de T , símbolo T + , al operador lineal T + : D (T + ) < H → H definido:
1) D(T + ) = { x ∈ H / ∃! g ∈ H : x, Ty = g , y ∀y ∈ D(T )} ≠ ∅ ,
2) x ֏ T + x = g ∀x ∈ D(T + ) .
∀T ∈ L( D(T ) < H , H ) , ∃!T + ∈ L( D(T + ) < H , H ) ⇔ D(T ) = H .
Propiedades: Sea T ∈ L( D (T ) < H , H ) con D (T ) = H (en particular,
∀A ∈ A ( H ) ), entonces:
∃!T + ∈ L( D(T + ) < H , H ) y es cerrado.
Si T es cerrado ⇒ D(T + ) = H ⇒ ∃T ++ = T .
D(T + ) = H ⇔ T es cerrable.
Si D(T + ) = H ⇒ ∃T ++ = T .
© M.C. Boscá, U. de Granada
8
Si ∃T ++ ⇒ T ++ = T y
(T )
+
=T+.
( )
Si ∃T −1 con D (T −1 ) = H ⇒ ∃ T +
−1
y
(T )
+ −1
= (T −1 ) .
+
T + x, y = x, Ty ∀x ∈ D(T + ) , ∀y ∈ D(T ) .
∀Ti ∈ L( D(Ti ) < H , H ), D(Ti ) = H , i = 1, 2 ⇒
⇒ (T1 ⊂ T2 ⇒ T2+ ⊂ T1+ ) ; (α Ti ) + = α *Ti + ∀α ∈ k .
∀Ti ∈ L( D(Ti ) < H , H ) , i = 1, 2 , con D(Ti ) = D(T1 + T2 ) = H ⇒ (T1 + T2 ) + ⊃ T1+ + T2+ .
∀Ti ∈ L( D (Ti ) < H , H ) , i = 1, 2 , con D(Ti ) = D(T1T2 ) = H ⇒ (T1T2 ) + ⊃ T2+T1+ .
Operadores hermíticos y autoadjuntos
Dado un operador lineal T : D(T ) < H → H con D (T ) = H , se define como
operador hermítico o simétrico ⇔
Tx, y = x, Ty
∀x, y ∈ D(T ) ⇔ T ⊆ T + .
Todo T ∈ L( D (T ) < H , H ) hermítico es cerrable.
T ∈ L( D(T ) < H , H ) hermítico ⇒ T ⊆ T ++ ⊆ T + .
Dado un operador lineal T : D(T ) < H → H con D (T ) = H , se define como
operador autoadjunto ⇔ T + = T .
Postulado II de la Mecánica Cuántica: Cada observable de un sistema físico se
representa en el formalismo matemático de la Mecánica Cuántica mediante un operador
lineal autoadjunto que actúa en el espacio de Hilbert ( H complejo, k = ℂ , y separable)
del sistema físico considerado.
Dado un operador lineal T : D(T ) < H → H hermítico ( ⇒ D (T ) = H ), se
define como operador esencialmente autoadjunto cuando posee una única
extensión autoadjunta ⇔ T es autoadjunto ⇔ T + = T ++ ( T + es autoadjunto)
⇔ T =T+.
Dado T ∈ L( D (T ) < H , H ) hermítico ( ⇒ D (T ) = H ):
Puede poseer una, ninguna o varias extensiones autoadjuntas.
Si T es esencialmente autoadjunto, admite extensión propia única,
Text T , autoadjunta.
Si T es autoadjunto, no admite extensión propia autoadjunta.
T ∈ L( D(T ) < H , H )
autoadjunto
T ∈ A ( D(T )) , i.e., es continuo ⇔ D(T ) = H .
Dado
( ⇒ D (T ) = H ),
entonces
Dado T ∈ L( D (T ) < H , H ) hermítico ( ⇒ D (T ) = H ) con cierre autoadjunto,
es esencialmente autoadjunto.
Dado T ∈ L( D (T ) < H , H ) hermítico ( ⇒ D (T ) = H ):
T es autoadjunto ⇔ R (T + iI ) = R (T − iI ) = H .
T es esencialmente autoadjunto ⇔ R (T ± iI ) = H ⇔ ker(T + ± iI ) = {0} .
© M.C. Boscá, U. de Granada
9
T es autoadjunto ⇔ ( T cerrado y ker(T + ± iI ) = {0} ).
Bloque 1 de propiedades: Sea T ∈ L( D (T ) < H , H ) con D (T ) = H , entonces:
Si T hermítico ⇒ ( T es cerrable, ∃T ++ = T , T ⊂ T ++ ⊂ T + ).
Si T hermítico y T = T ++ T + ⇒ T es cerrado y no es autoadjunto.
Si T hermítico y T T ++ = T + ⇒ T tiene cierre autoadjunto (es
esencialmente autoadjunto) y no es autoadjunto.
Si T hermítico y cerrado ⇒ T = T = T ++ ⊆ T + .
Si T hermítico y cerrado ⇒ (T = T + ⇔ T + es hermítico) .
Si T hermítico y cerrado ⇒ T es autoadjunto.
Si T hermítico y T = T ++ = T + ⇒ T es autoadjunto y cerrado.
Si T es autoadjunto ⇒ T hermítico y cerrado.
( T hermítico con D (T ) = H ⇒ T es acotado ) ⇒ T autoadjunto.
Si T es hermítico con D (T ) ≠ H y T es acotado ⇒ T es
esencialmente autoadjunto.
Si T cerrado y T + hermítico ⇒ T autoadjunto.
Si dim H < ∞ ⇒ ( T hermítico ⇔ T autoadjunto).
Lema: Dado T ∈ L( H ) , tal que
x, Tx = 0 ∀x ∈ H ⇒
Si k = ℝ y T = T + ⇒ T = 0
Si k = ℂ ⇒ T = 0
Dado T ∈ L( D (T ) < H , H ) , k = ℂ ⇒
Si D (T ) = H y T es acotado ⇒
( T es autoadjunto ⇔
x, Tx ∈ ℝ ∀x ∈ H ).
Si T es hermítico ( ⇒ D (T ) = H ) ⇒
x, Tx ∈ ℝ ∀x ∈ D(T ) .
Nota: Considerados los operadores lineales T : D(T ) < H → H , D(T ) = H :
Existen operadores hermíticos no acotados no autoadjuntos.
NO existen operadores autoadjuntos no acotados con D(T ) = H .
Bloque 2 de propiedades (acotados): Sea A ∈ A ( D ( A) < H , H ) con
D( A) = H , entonces:
Si A hermítico ⇒ A+ = A .
Si A ∈ A ( H ) (esto es, D ( A) = H ) y A es hermítico ⇒ A+ = A , i.e., es
autoadjunto.
Si A hermítico ⇒ puede siempre extenderse a D ( A) = D ( A+ ) = H , de
forma que se obtiene un autoadjunto.
Dados Ai ∈ A ( D ( Ai )) , i = 1, 2 , autoadjuntos ( D( Ai ) = H ) ⇒
A1 + A 2 y α Ai , ∀α ∈ ℝ, autoadjuntos.
Dados Ai ∈ A ( D( Ai ) < H , H ) , i = 1, 2 , con D( Ai ) = D( A1 A2 ) = H ,
autoadjuntos ⇒ ( A1A 2 autoadjunto ⇔ A1 A2 = A2 A1 ).
Si A autoadjunto con R ( A) ⊂ D ( A)
© M.C. Boscá, U. de Granada
10
⇒ An , n = 0,1, 2,… es autoadjunto.
Dado A ∈ A ( D ( A) < H , H ) hermítico (⇒ D ( A) = H ) , entonces:
Si D ( A) ≠ H , A es esencialmente autoadjunto.
Si D ( A) = H , A es autoadjunto.
Dado A ∈ A ( H ) con k = ℂ ; entonces:
∃! expresión A = Ar + iAi con Ar , Ai ∈ A ( H ) y autoadjuntos.
1
1
Ar = ( A + A+ ) ; Ai = ( A − A+ ) .
2
2i
Es posible definir una relación de orden parcial (i.e.: no todos los
elementos serán ordenables) en el conjunto de los operadores acotados
autoadjuntos (tanto para k = ℝ como para k = ℂ ):
Sea AA = A ∈ A ( H ) / A+ = A , entonces:
{
}
Dados A, B ∈ AA : A ≤ B ≡ B ≥ A ⇔
x, Ax ≤ x, Bx ∀x ∈ H
Si A ≤ B ⇒ A+C ≤ B+C ∀ A, B, C ∈ AA
Si A ≤ B ⇒ α A ≤ α B ∀α ∈ ℝ, α ≥ 0 ∀ A, B ∈ AA
Operadores positivos
operador lineal T : D(T ) < H → H hermítico (⇒ D ( A) = H ) , se
Dado un
x, Tx ≥ 0 ∀x ∈ D(T ) .
define como operador positivo ⇔
Dados T1 y T2 operadores positivos ⇒
T1 y T2 conmutan.
Su producto no es, en general, un operador positivo.
Todo operador A ∈ A ( H ) positivo es A ≥ 0 y autoadjunto.
Dado A ∈ A ( H ) ⇒ AA+ y A+ A son acotados, autoadjuntos y positivos.
Dado A ∈ A ( H ) positivo ( ⇒ A es autoadjunto) ⇒
A + I es invertible
1
1
∃! B = A 2 ∈ A ( H ) , operador raíz cuadrada de A , A 2 , tal que B 2 = A .
1
1
1
1
A 2 ∈ A ( H ) ; A 2 ≥ 0 y ( A 2 )+ = A 2 .
Dado
A ∈ A ( H ) se define el operador módulo de
A,
1
2
A = ( A+ A) .
= A ; ( A = A+ ⇔  A, A+  = 0 ).


-Nota: en general, A + B ≤ A + B , AB ≠ A B y A − B
A ≥ 0;
A
© M.C. Boscá, U. de Granada
11
≤ A− B .
A , como
Proyectores ortogonales (⊂ A )
Proyectores ortogonales
Definición: Dados un espacio euclídeo L y dos subespacios lineales M 1 < L
y M 2 < L tales que L = M 1 ⊕ M 2 , un proyector de L sobre M 1 en la dirección
de
M2 ,
PMM1 2 ≡ PM1 : L → M 1 , se dice que es un proyector ortogonal
⇔ M1 ⊥ M 2 .
Dado P ∈ A ( H ) , se define como un proyector ortogonal sii P = P + = P 2 .
Dados un proyector ortogonal P y el operador identidad I en L ⇒ el
operador I − P es proyector ortogonal con recorrido R ( I − P ) = ker P y núcleo
ker ( I − P ) = R ( P ) .
{}
Todo proyector ortogonal PM es continuo, positivo, P ≥ 0 , y, sii M ≠ 0 y
P ≠ 0 , posee norma unidad.
Dado P proyector ortogonal en L ⇒
ker P ⊲ L y R ( P ) ⊲ L
ker P = ( R ( P )) ⊥ y R ( P ) = (ker P )⊥
Dados dos subespacios lineales M < L y N < L tales que L = M ⊕ N y
M ⊥ N , entonces ⇒ ∃! (existe un único) proyector ortogonal P con R ( P ) = M
y ker P = N = M ⊥ .
-Nota: Obsérvese que, dado un M ⊲ L , no está garantizado que exista un proyector
ortogonal PM , o sea, no siempre se tendrá L = M ⊕ M ⊥ (algo que sí ocurre cuando el
espacio es completo, esto es, un Hilbert).
Dado un operador lineal P ∈ L( H ) , P es un proyector ortogonal ⇔ P 2 = P y
x, Py = Px, y
∀x, y ∈ H (esto es, sii P es idempotente y autoadjunto).
Dados Pi ∈ A ( H ) ,proyectores ortogonales con recorrido M i = R ( Pi ) ⊲ H ,
i = 1, 2 :
P1 P2 es proyector ortogonal sobre M 1 ∩ M 2 ⇔
[ P1 , P2 ] = 0 .
P1 + P2 es proyector ortogonal sobre M 1 ⊕ M 2 ⇔ M 1 ⊥ M 2 .
P1 P2 = P1 ⇔ M 1 ⊂ M 2 .
P2 − P1 es proyector ortogonal sobre M 1⊥ ∩ M 2 ⇔ M 1 ⊂ M 2 ( P1 ≤ P2 ).
Dada la sucesión
{Pn }n =1
∞
con Pm ≤ Pn si m < n
proyector ortogonal sobre
∪M
n
© M.C. Boscá, U. de Granada
12
n
.
⇒
Pn → P con P
Operadores normales
operador lineal N : D ( N ) = H → H con D ( N ) = H , se define
Dado un
como operador normal ⇔ N + N = NN + (i.e.:  N , N +  = 0 , o sea, conmutan).
operador lineal T : D(T ) = H → H con D (T ) = H , es operador
Dado un
Tx = T + x ∀x ∈ H ⇔ T + es operador normal.
normal ⇔
Todo operador autoadjunto acotado es normal.
operador lineal acotado A ∈ A ( H ) con k = ℂ , es operador
Dado un
normal ⇔
[ Ar , Ai ] =0 , con
Ar =
1
( A + A+ ) y
2
Ai =
1
( A − A+ ) .
2i
Propiedades:
Dado un operador normal acotado N ⇒
N2 = N .
2
Dado un operador lineal T : D(T ) = H → H , T operador autoadjunto
⇒ T es normal.
Si N i : D ( N i ) = H → H , i = 1, 2 , normales ⇒ N1 + N 2 y α N i , ∀α ∈ k,
normales; N1 N 2 normal ⇔  N1 , N 2+  =  N 2 , N1+  = 0 .
Dada { N i }i =1 , sucesión de operadores N i : D ( N i ) = H → H , i = 1, 2 ,
∞
normales acotados, N i → T , T operador acotado ⇒ T operador
normal.
Operadores isométricos (⊂ A )
Dado un operador lineal T : D (T ) < L1 → L2 con D(T ) = L1 , se define como
operador isométrico ⇔
Dado un
isométrico ⇔
isométrico ⇔
2
∀x ∈ D(T ) .
operador lineal T : D (T ) < L1 → L2 con D(T ) = L1 , es operador
Tx, Ty
2
= x, y
Dado un operador T
singular y con T = 1 .
Dado un
Tx 1 = x
1
∀x, y ∈ D(T ) .
lineal e isométrico ⇒ T
es operador acotado, no-
operador lineal T : D(T ) = H → H con D (T ) = H , es operador
T +T = I D (T ) (restricción de la identidad a D(T ) ).
© M.C. Boscá, U. de Granada
13
Operadores unitarios (⊂ A )
Dado un operador lineal acotado U ∈ A ( H ) , se define como operador
unitario ⇔ es un isomorfismo isométrico ⇔ es una biyección lineal y
Ux,Uy = x, y ∀x, y ∈ H (se tiene D(U ) = R (U ) = H ).
Dado un operador lineal acotado U ∈ A ( H ) , es unitario ⇔
+
−1
+
+
U
es
+
invertible y U = U
⇔ U es invertible y U U = UU = I ⇔ U es unitario
⇔ U transforma una base ortonormal de H en otra base ortonormal de H .
Dados dos operadores unitarios U1 , U 2 ∈ A ( H ) ⇒ su producto es también
un operador unitario U1U 2 ∈ A ( H ) .
Dado T ∈ A ( H ) con H de dimensión finita, si es operador isométrico, es
unitario.
Todo operador unitario es normal.
Dado
T ∈ L( D(T ) < H , H )
y
definido
el
operador
unitario
+
U ∈ A ( H ⊕ H ) : U ( x, y ) = (− y, x) ∀( x, y ) ∈ H ⊕ H , tal que U = −U , se tendría,
supuesto que el operador poseyera adjunto, que:
∀ x ∈ D(T + ) ∀ y ∈ D(T ) : T + x, y = x, Ty ⇔
⇔ ( x, T + x), U ( y, Ty ) = 0 ⇔ η (T + ) = (U (η (T ))) ⊥ ,
de forma que siempre que el complemento ortogonal de la acción del
operador U sobre el gráfico del operador T sea el gráfico de un operador
lineal, entonces puede definirse T + , lo que ocurre para operadores con
dominio denso, D (T ) = H .
Dados dos operadores lineales Ti : D (Ti ) < H → H , i = 1, 2 , se definen como
operadores unitariamente equivalentes ⇔ existe un operador unitario
U ∈ A ( H ) tal que U ( D(T1 )) = D(T2 ) y T2 = U −1TU
.
1
La equivalencia unitaria es una relación de equivalencia en la clase de
todos los operadores lineales T : D(T ) < H → H .
Dados operadores lineales, uno
A : D( A) < H → H
acotado y otro
T : D(T ) < H → H , unitariamente equivalentes ⇒ T es acotado y T = A .
Dados
autoadjunto,
operadores
o
lineales,
unitario)
y
uno
otro
T1 : D(T1 ) < H → H
T2 : D(T2 ) < H → H ,
hermítico
(o
unitariamente
equivalentes ⇒ T2 es hermítico (autoadjunto, unitario).
Dados los operadores unitarios An , A , Bn , B ∈ A ( H ) tales que An 
→A y
Bn 
→ B ⇒ An Bn 
→ AB .
© M.C. Boscá, U. de Granada
14
Mecánica Cuántica: El operador de evolución temporal para un vector estado
ψ (t ) , i.e.: ψ (t ) = U (t , t0 ) ψ (t0 ) , es un operador lineal unitario; para un sistema
conservativo, U (t , t0 ) = exp[−i (t − t0 )E / ℏ] es el operador evolución temporal para los
estados estacionarios o estados propios de H con autovalor E (energía),
H ψ (t0 ) = E ψ (t0 ) , donde H es el Hamiltoniano del sistema.
Operador de Fourier-Plancherel:
(
)
-Se trata del operador unitario F ∈ A L2 ( ℝ ) tal que ∀f , g ∈ L2 ( ℝ ) :
+∞
− ixy
i d e −1
f ( x)dx c.d.
∫
2π dy −∞ x
(Ff )( y ) =
+∞
−i d e + ixy − 1
g ( y )dy c.d. ,
∫
2π dx −∞ y
extensión a todo L2 ( ℝ ) del operador que da la transformación de Fourier
(F −1 g )( x) =
sobre las funciones de la envolvente lineal de la b.o.n. de L2 ( ℝ ) :
∀f , g ∈ {en }n∈N 
/
(Ff )( y ) =
1
2π
+∞
∫e
− ixy
f ( x)dx ∀y ∈ ℝ ,
−∞
+∞
1
(F −1 g )( x) =
e+ ixy g ( y )dy ∀x ∈ ℝ .
∫
2π −∞
(Ampliar: Abellanas y Galindo, pp. 188ss.).
Operadores compactos (⊂ A ; C ( H )<A ( H ))
Dado un operador lineal T : D (T ) = L1 → L2 con D(T ) = L1 , se define como
operador compacto o completamente continuo ⇔
⇔ dada la bola unidad B = { x ∈ L1 / x 1 ≤ 1} , se tiene que T ( B ) es compacto
⇔ ∀ { xn }n =1 ⊂ B ⇒
∞
{Txn }n=1 ⊂ T ( B)
∞
contiene alguna subsucesión
convergente (en T ( B ) ).
⇔ ∀ { xn }n =1 ⊂ L1 , sucesión acotada, ⇒
∞
{Txn }n =1 ⊂ L2
∞
contiene alguna
subsucesión convergente (en L2 ).
⇔ ∀S ⊂ L1 , subconjunto acotado, ⇒ T ( S ) es compacto.
⇔ transforma sucesiones débilmente convergentes en sucesiones fuertemente
convergentes (nota: ver tema 5 para estos dos conceptos).
Propiedades:
Todo operador compacto es
acotado (nota: existen operadores acotados no
L1 con dimensión no finita, el operador identidad I : L1 → L1 no es compacto; en
dimensión finita, un operador es lineal ⇔ es acotado ⇔ es compacto).
Todo operador acotado degenerado (i.e.: de rango finito, dim R (T ) finita)
compactos; e.g.: para
es compacto.
© M.C. Boscá, U. de Granada
15
C operador compacto ⇒ C + compacto.
A operador acotado y A+ compacto ⇒ A compacto.
Dado C ∈ C ( H ) ⇒ ∃ x ∈ D (C ) , con norma x = 1 , tal que Cx = x .
C operador compacto ⇔ C operador compacto.
Sea C ( H ) el conjunto de los operadores C : D (C ) = H → H compactos.
Propiedades:
C (H ) < A (H )
∀C ∈ C ( H ), ∀A ∈ A ( H ) ⇒ CA ∈ C ( H ), AC ∈ C ( H )
u
→ C ⇒ C ∈ C (H )
{Cn } ⊂ C ( H ), Cn 
{ An } ⊂ A ( H ), A n
Sea T =
u
degenerado ∀n, A n 
→ A ⇔ A ∈ C (H )
N
∑λ P , N < ∞ ,
n =1
n n
con Pn proyector ortogonal ∀n , λn Pn ≠ 0 ∀n y
Pn ⊥ Pm si n ≠ m ; entonces T es compacto ⇔
Sea T =
∞
∑λ P
n =1
n n
, con Pn proyector ortogonal ∀n , λn Pn ≠ 0 ∀n y Pn ⊥ Pm si
Pn es degenerado ∀n y lim λn = 0 .
n ≠ m ; entonces T es compacto ⇔
Sea
Pn es degenerado ∀n .
C ∈C (H ) , C
n →∞
N
C = ∑ λn Pn , N < ∞ , con Pn
⇒
operador normal
n =1
proyector ortogonal degenerado ∀n , λn Pn ≠ 0 ∀n y Pn ⊥ Pm si n ≠ m , o bien
∞
C = ∑ λn Pn con Pn proyector ortogonal degenerado ∀n , λn Pn ≠ 0 ∀n , Pn ⊥ Pm
n =1
si n ≠ m y lim λn = 0 .
n →∞
Sean {en }n =1 y {e´n }n =1 dos bases ortonormales numerables del espacio H .
∞
∞
Lema: Dado A ∈ A ( H ) tal que
∑
Aen
2
< ∞ , ∀ {e 'n } , b.o.n. de H ⇒
n
∑
n
Aen
2
= ∑ e 'm , Aen
n ,m
© M.C. Boscá, U. de Granada
2
= ∑ Ae 'n
n
2
= ∑ A+ en
n
16
2
= ∑ A + e 'n
n
2
.
Operadores de la clase Hilbert-Schmidt (C 2 < C )
Dado A ∈ A ( H ) , se define
A
2
≡ A 2 = ∑ Aen
2
2
.
n
Dado A ∈ A ( H ) , se define
A como operador perteneciente a la clase
A ≡ A 2 < +∞ .
Hilbert-Schmidt, o de Hilbert-Schmidt, sii
Propiedades:
∀A ∈ A ( H ) ⇒
A ≤ A2
∀A ∈ A ( H ) , A 2 = 0 ⇔ A=0
Sea C 2 ( H ) el conjunto de los operadores C2 : D (C2 ) = H → H de la clase
Hilbert-Schmidt.
Propiedades:
i define una norma en C 2 ( H ) (norma Hilbert-Schmidt).
(C 2 ( H ), i ) es Hilbert; C2 , B2 =
∑
Ben , Cen , C2 , B2 ∈ C 2 ( H ) .
en ∈b.o .n.
C2 (H ) < C (H ) < A (H ) .
∀C ∈ C 2 ( H ) ⇒ C + ∈ C 2 ( H ) y C 2 = C + .
2
C ∈ C2 (H ) ⇔ C ∈C2 (H ) .
∀C ∈ C 2 ( H ), ∀A ∈ A ( H ) ⇒ CA ∈ C 2 ( H ), AC ∈ C 2 ( H ) .
∀C ∈ C 2 ( H ), ∀A ∈ A ( H ) ⇒ CA 2 ≤ C
2
A ,
AC 2 ≤ C
2
A.
Operadores integrales de Hilbert-Schmidt:
K ∈ A ( L2 ([ a, b ]) ) , con dominio todo el
Operador lineal continuo
espacio y regla de actuación
(K f ) ( x) = ∫ K ( x, y) f ( y)d y , con K ( x, y ) ∈ L2 ([ a, b ] × [ a, b ]) .
b
a
Operador lineal continuo K
∈ A ( L2 ( ℝ ) ) , con dominio todo el espacio
y regla de actuación
(K f ) ( x) = ∫ K ( x, y ) f ( y)d y , con K ( x, y ) ∈ L2 ( ℝ 2 ) .
ℝ
Propiedad:
K f ≤ K ⋅ f , por lo que K ≤ K .
-Nota: estos operadores aparecen en la teoría de ecuaciones integrales.
© M.C. Boscá, U. de Granada
17
Operadores de la clase traza (C1 < C 2 )
Dado A ∈ A ( H ) se define como operador de la clase traza C1 ( H ) o
1
trazable sii A 2 ∈ C 2 ( H ) .
Dado A ∈ A ( H ) , se define A 1 ≡ tr A =
Dado A ∈ A ( H ) , A ∈ C1 ( H ) ⇔
∑
en ∈b.o .n.
1 2
1
A 2 en = ∑ en A en = A 2 .
n
2
A 1 < +∞ .
Propiedades:
∀A ∈ A ( H ) , A ∈ C1 ( H ) ⇔ A ∈ C1 ( H ) ⇔ A=BC con B,C ∈ C 2 ( H ) .
⋅ 1 ≡ tr A define una norma en C1 ( H ) (norma traza).
(C1 ( H ), ⋅ 1 ) es Banach.
∀C ∈ C1 ( H ) ⇒ C + ∈ C1 ( H ) y C 1 = C + .
1
C1 ( H ) < C 2 ( H ) < C ( H ) < A ( H ) .
∀C ∈ C1 ( H ) ⇒ C ≤ C 2 ≤ C 1 .
∀C ∈ C1 ( H ), ∀A ∈ A ( H ) ⇒ CA ∈ C1 ( H ), AC ∈ C1 ( H ) .
∀C ∈ C1 ( H ), ∀A ∈ A ( H ) ⇒ CA 1 ≤ C
1
A ,
AC 1 ≤ C
1
A .
Dado C ∈ C1 ( H ) , se define su traza, tr C , como el escalar
tr C =
∑
en , Cen .
b. o. n.
La aplicación tr : C1 ( H ) → ℂ satisface:
tr C + = ( tr C ) .
*
∀λ ∈ ℂ ⇒ tr (λC ) = λ tr C .
tr (C+B) = tr C + tr B .
C ∈ C1 ( H ), A ∈ A ( H ) ⇒ tr CA = tr AC .
tr C ≤ tr C .
Operadores densidad (∈ C1 ) y estados en
Mecánica Cuántica (cf. Abellanas y Galindo, pp. 211-212)
Mecánica Cuántica: Los estados físicos de un sistema cuántico se definen
como aplicaciones del conjunto P ( H ) de los proyectores ortogonales en H
(recuérdese: separable y complejo) sobre el intervalo [ 0,1] , p : P ( H ) → [ 0,1] , de
forma que p ( P ) representa la probabilidad de que al medir el observable P
en el estado p resulte el valor 1.
Estas aplicaciones deben cumplir:
© M.C. Boscá, U. de Granada
18
a) p (0) = 0, p (1) = 1
b) ∀i ≠ j : p (
∞
∞
i =1
i =1
∑ Pi ) = ∑ p( Pi ) siempre que Pi ⊥ Pj .
El teorema de Gleason asegura que, si dim H ≥ 3 ⇒ ∀p ∃ρ ∈ C1 ( H ) ,
autoadjunto ( ρ + = ρ ) y positivo ( ρ ≥ 0) , tal que tr ρ = 1 y p ( P ) = tr ( ρ P ) ∀P .
Estos operadores ρ , que representan los estados del sistema físico, se
denominan operadores densidad.
Dados dos operadores densidad, ρ1 y ρ 2 ⇒ toda combinación lineal
convexa, esto es, de la forma ρ = λ1 ρ1 + λ2 ρ 2 , λ1 , λ2 ≥ 0, λ1 + λ2 = 1 , representa
otro operador densidad.
Mecánica Cuántica: Un operador densidad expresable como combinación
lineal convexa de otros dos, con ρ = λ1 ρ1 + λ2 ρ 2 , λ1 , λ2 ≥ 0, λ1 + λ2 = 1 , con
λ1λ2 ≠ 0 , define un estado impuro o estado mezcla del sistema; si λ1λ2 = 0 el
estado se define como estado puro.
Todo operador compacto normal C
(en particular, todo operador
autoadjunto de clase traza) admite expresión C =
∞
∑λ P ,
n n
Pn ⊥ Pm si n ≠ m .
1
Todo operador densidad (que, por serlo, es positivo) admite expresión
∞
ρ = ∑ λn Pn , λn ≥ 0, Pn ≠ 0 ∀n y Pn ⊥ Pm si n ≠ m .
1
Como tr ρ = 1 , se tiene
∞
∑ λ tr P
n
n
= 1 ⇒ ( Pn ,
λn ≠ 0 ⇒ Pn de rango finito) .
1
Y, supuestos dos λ1 y λ2 no nulos, entonces:
 P1 
 λ2 P2 + ⋯ 
 + (1 − λ1trP1 ) 
 , siendo 1 − λ1trP1 ≠ 0 ,
tr
P
1
−
tr
P
λ
 1

1
1 
ρ = λ1P1 + λ2 P2 + ⋯ = λ1trP1 
ya que λ2 ≠ 0 .Luego
dos operadores
el operador ρ es combinación lineal convexa de los
P1
ρ − λ1P1
y
.
trP1
1 − λ1trP1
Consecuentemente, ρ es puro ⇔ ρ es un proyector unidimensional
⇔ trρ 2 = 1 . En este caso es frecuente identificar el estado ρ con uno
cualquiera de los vectores de norma 1 que engendran el subespacio de
proyección de ρ .
© M.C. Boscá, U. de Granada
19