conductividades termicas a par

ISSN -0325-4011
Lat. am. j. heat mass. transf.
References
le, edited by S. Angus, B. Arms·
Rev. latinoam. transf. cal. mat.
6: 181-190 (1982)
Lat. am. j. heat mass. transf.
COMMUNICATION
COMUNICACION
unic properties near the critical
:biger thermodynamischer. Zusg.-Wes. 45 Nr. 1 (1979).
0 2 im 2 • Phasen-Gebiet", theoReceived: July 7, 1982
Accepted: July 28, 1982
DISPERSION DE RADIACION Y TRANSFERENCIA DE CALOR EN
ESPUMAS PLASTICAS: CONDUCTIVIDADES TERMICAS A PARTIR
DE ESPECTROS INFRARROJOS
RADIATION SCATTERING AND HEAT TRANSFER IN CELLULAR
PLASTICS: THERMAL CONDUCTIVITIES FROM INFRARED SPECTRA
VALENTIN T. AMOREBIETA, AGUSTIN J. COLUSSI
Departamento de Quimica, Universidad de Mar del Plata, 7600 Mar del Plata, Argentina
Resumen
Abstract
El mecanismo de flujo de calor radiante en materiales celulares es analizado en terminos de sus propiedades espectrales en la zona de infrarrojo. Especificamente, se encontro que espumas comerciales de poliestireno con diametros de celda de alrededor de
100-150 µm se comportan como medios dispersantes
6pticamente densos hasta cerca de 8 µm. A longitudes
de onda mas largas, es decir, en la region donde los
cuerpos negros presentan la maxima potencia emisiva
a temperatura ambiente, el coeficiente de dispersion
disminuye marcadamente y el material se vuelve casi
transparente por encima de 50 µm. El comportamiento de a en esta region critica no sigue una ley
simple del tipo .,_ - n, indicando que el proceso debe
clasificarse como dispersion de Mie. Se muestra como a partir de esta informaci6n, codificada en la forma de Ull coeficiente efectiVO de dispersion, la COn·
ductividad termica neta se puede calcular mediante
tecnicas usuales ya desarrolladas. Las bases fisicas que
relacionan la estructura celular y el flujo neto de calor
en estos materiales quedan as{ establecidas.
The mechanism of radiative heat flow in cellular
materials is analyzed in terms of their spectral properties in the infrared region. Specifically, it was found
that commercial polystyrene foan1s having average
cell diameters of 100-150 µm behave as optically
dense scattering media up to about 8 µm. At longer
wavelengths, i.e. in the region where black bodies
display their maximum emissive power at ambient
temperatures, the scattering coefficient a markedly
decreases and the material becomes almost transparent above 50 µm, The behavior of a in thls critical region does "not follow a simple .,.. - n law,·
revealing that the process should be classified as Mie
scattering. It is shown that from this infonnation,
encoded as an effective scattering coefficient, overall
thermal conductivities can be actually derived by
means of standard techniques dealing with energy
transfer in scattering media. The physical basis for
relating cellular structure . and net heat flow in
plastic foams is thereby established.
lntroducci6n
Introducction
Las espumas plasticas r{gidas proveen aislaci6n termica eficiente a temperatura ambiente y
subambiente. Por esta raz6n se estima que su
demanda llegara al 35 % del mercado de poliestireno y poliuretano hacia 1985 debido a costos
de energ{a crecientes. Parece as{ justificado
retomar la investigaci6n del mecanismo de flujo
de calor en estos materiales.
Rigid plastic foams provide highly efficient
thermal insulation at ambient and subambient
temperatures. For this reason it is expected that
their demand will increase up to a 35 % share of
the polystyrene and polyurethane markets by
1985 due to rising energy costs (Chem. Eng.
News, 1980). Thus further research on the
mechanism of heat flow in these materials
seems entirely justified.
181
Rev. latinoam. transf. cal. mat.
Lat. am. j. heat mass. transf.
Las espumas comerciales consisten en celdas de gas de tamafio uniforme distribuidas regularmente en una matriz homogenea y continua de polimero. Los tamafios corrientes de celda y de pared de celda varian entre 100-380 µm
y 1-5 µm, respectivamente. El sistema compuesto se puede caracterizar por su densidad neta y
el valor de Xg.
Esencialmente, los linicos mo dos que deben
ser considerados en la transferencia de energia
son conducci6n y radiaci6n, dado que se puede
demostrar que la convecci6h dentro de las burbujas es despreciable para los tamafios de celda usuales. Suponiendo, ademas, que los dos
modos se<pueden tratar separadamente y considerando que la conducci6n por el s6lido es
despreciable, resulta evidente que los dos procesos a tratar son conducci6n gaseosa y transferencia de radiaci6n a traves de todo el material. La estimaci6n de conductividades termicas
de plasticos celulares se reduce al problema de
predecir sus propiedades 6pticas en el infrarroj o. Dado que un solido finamente dividido en
particulas de tamafios comparables a la longitud de onda de la radiacion incidente se comporta de modo muy diferente a la del material
compacto, es preciso considerar no solo la absorci6n de radiacion sino tambien su dispersion.
Las correlaciones empmcas corrientes que
vinculan k con p no logran incorporar la transferencia por radiacion, y por consiguiente fallan
al ser extendidas a temperaturas elevadas, es
decir, a las condiciones que prevalecen en el
procesado de pol{meros.
Un modelo reciente propone una distribucion regular de pianos semitransparentes para
explicar la transferencia de radiacion, pero no
incorpora la dependencia espectral de los parametros 6pticos.
En este trabajo relacionamos cuantitativamente la transmision de capas delgadas de espuma de poliestireno en la region del infrarro. jo con sus propiedades termicas. Este enfoque
lleva a la conclusion especifica que las propiedades aislantes se pueden mejorar significativamente reduciendo la transparencia por encima
de 8 µm. Estamos investigando c6mo lograr
este objetivo.
Commercial foams consist of uniformly
seized discrete gas filled cells imbedded in a
homogeneous, continuous polymer matrix,
Average cell diameters Xg and cell wall thicknesses x 8 vary between 100-380 µm and 1-5
µm 1 respectively. The composite system is usually characterized by its overall density Pf and
Xg values..
.
Essentially, conduction and radiation are
the only modes to be considered in thermal
energy transfer through- the solid and gas phases,
since convection within the gas bubbles is
negligible in the rage of Xg values normally
available (Progelhof et al., 1976; Eckert and
Drake, 1972). Assuming that the two effective
modes can be treated separately (Siegel and
Howell, 1972) and considering that solid
conduction only amounts to a small fraction ·
of the combined heat flow, it follows that the
dominant processes are simply gas conduction ·
and radiation transfer through the entire material. Thus, estimation of thermal conductivi·
ties for cellular plastics reduces to the basic
problem of predicting their transmission properties in the infrared region. Since a finely
divided solid in the form of small particles
whose seizes are comparable to the wavelength
of incident radiation behave very differently
from the same material in the bulk form, absorption as well as radiation scattering must be
considered in general.
Current empirical correlations between ther·
mal conductivities and foam density overlook
the role of radiative transfer (Progelhof, 1976)
and therefore they can hardly be extended to ·
higher temperatures, i.e. the conditions prevailing in polymer processing (Progelhof and'
Throne, 1975).
A recently proposed geometrical model of
a foam deals explicitly with radiation transfer
without incorporating the spectral dependence
of the optical parameters (Marciano et al.
1980).
In this communication we are able to
quantitatively relate the infrared transmission
spectra of thin layers of polystyrene foams
with experimental data on thermal conductivi·
ties ..This approach leads to the specific con·
clusion that insulating properties can be sig·
nificantly improved by reducing transparency
above 8 µm. The ways to achieve this goal are
being investigated.
182
Parte experimental
Una muestra comerc
forma de espuma inflad:1
pleado como material de
da en todos los experime ·
El material era de tex
nes de densidad en pore
sultado muy reproducib ,
La examinacion microsc
de 0,5 mm de espesor
de panal muy unifom1e
angosta de tamafios Xg
celulas) Y Xs = 4 µm.
La conductividad te
pianos (30 X 3 cm) fue
Los discos se mantuvie,
de acero termostatizad<1
axial de 20 K hasta qu,
estado estacionario. El V<•
X 10- 2 W m- 1 K- 1 cc
literatura para materiales .
Los espectros infram
das de espuma se registr1
fotometro Perkin-Elmer::
Las muestras fueron con
mo manual y montadas
cuado. Con el objeto Ci
error introducido por · p1
transmitancia de las mue
plicados. Para minintizar .
cion de propagaci6n del
secciones de los haces de l
por un factor diez sin ei
ficos absorbancia vs. espes
coeficientes de extincion
mos se presentan en la tab
TABLA 1
TABLE
A. (µm)
(a+ a) cm
*
Coeficie•
cia (A.)/ S
* Extinctioi
Lat. am. j. heat mass. transf.
foams consist of unifonnly
as filled cells imbedded in a
:ontinuous polymer matrix;
neters Xg and cell wall thicketween 100-380 µm and 1-5
fhe composite system is usual.
by its overall density Pf and
mduction and radiation are
to be considered in thennal
rough- the solid and gas phases,
within the gas bubbles is
rage of Xg values normally
10f et al., 1976; Eckert and
suming that the ·two effective
reated separately (Siegel and
and considering that solid
amounts to a small fraction
heat flow, it follows that the
es are simply gas conduction ·
nsfer through the entire ma.
nation of thermal conductiviplastics reduces to the basic
icting their transmission profrared region. Since a finely
the form of small particles
:omparable to the wavelength
ltion behave very differently
1aterial in the bulk form, abs radiation scattering must be
~ral.
cal correlations between thers and foam density overlook
ive transfer (Progelhof, 1976)
y can hardly be extended to
·es, i.e. the conditions prevail·
processing (Progelhof and
>posed geometrical model of
licitly with radiation transfer
1ting the spectral dependence
>arameters (Marciano et al.
mnication we are able to
1te the infrared transmission
.ayers of polystyrene foams
l data on thermal conductivi·
)h leads to the specific con·
lating properties can be sig·
ed by reducing transparency
ways to achieve this goal are
VALENTIN T. AMOREBIETA, AGUSTIN J. COLUS.SI
Parte experimental
Experimental
Una muestra comercial de poliestireno en
forma de espuma inflada con aire del tipo empleado como material de empaque fue empleada en todos los experirnentos.
.
A sample of commercial air-filled polystyrene foam used as packing material was selected. Its density Pf> microscopic structure, apparent thermal conductivity and infrared spectra were determined.
El material era de textura pareja y medicioThe material was evenly textured and densines de densidad en porciones diferentes un re- · ty measurements from different portions were
sultado muy reproducible Pf = 19 $ Kg m- 3 • quite reproducible yielding a value of Pf =
La examinaci6n microsc6pica de una hojuela 19 .8 Kg m - 3 • Microscopic examination of a
de 0 ,5 mm de espesor reve16 una estructura 0 .5 mm thick sheet revealed an uniform honeyde panal muy uniforme con una distribuci6n comb structure and a rather narrow size disangosta de tamafios Xg = 160 ± 40 µm (10 tribution with cell diameters Xg = 160 ± 40
µm (10 cells) and a wall thickness· Xs = 4 µm.
celulas) Y Xs = 4 µm.
La conductividad termica neta de discos
The overall thermal conductivity of flat
planos (30 X 3 cm) fue determinada a 310 K. (30 X 3 cm) discs was determined at 310 K.
Los discos se mantuvieron entre dos placas The discs were kept between two thermostatde acero termostatizadas bajo un gradiente ted steel plates under a 20 K gradient until the
axial de 20 K hasta que el equipo alcanzara insulated assembly reached steady state. The
estado estacionario. El valor medido ka = 4$3 measured value ka = 4.83 X 10- 2 W m- 1 K-1
X 10- 2 W m - 1 K - 1 concuerda con datos de agrees well with literature data for materials of
literatura para materiales analogos.
similar density, within experimental error
(15%).
The infrared spectra of thin sheets, 0.25 to
Los espectros infrarrojos de 13minas delgadas de espuma se registraron con un espectro- 1 5 mm thick were recorded with a doublefot6metro Perkin-Elmer 599 entre 2,5 y 50 µm. beam Perkin-Elmer 599 spectrophotometer
Las muestras fueron cortadas con un micr6to- from 2.5 to 50 µm. The samples were sliced
mo manual y montadas sobre un soporte ade- with a manual microtome and mounted on a
cuado. Con el objeto de eliminar el posible liquid cell holder assembly. To eliminate the
error introducido por · poros minusculos en la possible error introduced by small pore. irp.transmitancia de las muestras se corrieron du- perfections on the effective light transmission,
plicados. Para minimizar dispersion en la direc- duplicate runs of different sheets were taken.
ci6n de propagaci6n del haz se redujeron las In order to eliminate forward scattering, the
secciones de los haces de prueba y de referencia sample and reference beam cross sections were
por un factor diez sin efecto apreciable. Gra- reduced by a factor of ten without appreciable
ficos absorbancia vs. espesor fueron lineales; los effect on the spectra. Linear plots of absorbcoeficientes de extinci6n derivados de los mis- ence vs. sample thickness were obtained at
all wavelengths. The derived extinction coefmos se presentan en la tabla 1.
ficients are pressented in table 1.
TABLA 1.- Coeficiente de extincion de espumas de polietireno a 300 K*
TABLE 1.-Extinction coefficients of polystyrene foams at JOO K*
A. (µm)
(a+ a) cm· 1
5
10
15
20
25
36.8
29.8
21.2
15.8
10.7
*
30
35
40
45
50
8.0 5.9 4.4 3.9 3.4
Coeficientes de extinci6n obtenidos como (a+ a)A. = 2.303 Absorbancia (A.)/ R,.
* Extinction coefficients obtained as (a + a)A. = 2.303 Absorbance (A.)/ R,
183
Lat. am. j. heat mass. transf.
Rev. latinoam. transf. cal. mat.
Resultados y discusi6n
Results and discussion
El mecanismo de transmision de calor
por radiaci6n
The mechanism of radiation heat transfer
La radiaci6n tennica que incide sobre una
lamina de espuma de poliestireno es parcialmente absorbida pero otra parte se deflecta por
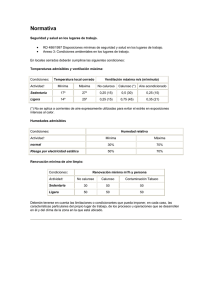
dispersi6n (fig. 1). Los detalles discretos del espectro de la figura 1 corresponden a vibraciones
moleculares de poliestireno. Sin embargo, la
mayor parte de la radiaci6n se elimina por dis·
persi6n, como queda evidenciado por la dependencia inversa del fondo continuo con X. Una
representaci6n del material como un conjunto
uniforme polidisperso de prismas chatos dis·
puestos al azar, las paredes de las celdas, con
dimensiones promedio de 50 X 50 X 4-µm es
consistente con dichas observaciones. Ademas,
las part{culas dispersoras irregulares se pueden
considerar para este efecto como equivalentes a
esferas con un diametro medio de D "' 25 µm;
por consiguiente, la relaci6n per{metro-longitud
de onda (7T D/X) var{a entre 1,7 y 34.ElHmite
inferior que se alcanza en el limite rojo del espectro es todav{a mayor que el requerido para
la dispersi6n de Rayleigh. Por otro lado, para
valores superiores a 10 la interacci6n se puede
describir simplemente como un proceso de reflexi6n y difracci6n no selectivo. El rango que
cubre la mayor parte de la curva de emisi6n de
un cuerpo negro a 300 K corresponde al domi·
nio de la teoria de la dispersion de Mie.
Thermal radiation impinging upon a layer
of polystyrene foam is partly removed by
absorption and in part redirected by scattering (fig. 1). The discrete features of the
spectrum in figure 1 correspond to molecular
vibrations of polystyrene. However, most of
the radil!,tion is indeed removed by scattering,
as evidenced by the inverse dependence of the
continuous background with X. A picture of
the material as an uniform polydisperse arrangement of randomly oriented flat prisms, the cell
faces, with average dimensions of 50 X 50 X 4
µm is consistent with the above observations.
Moreover, the irregular scattering particles can
be justifiably considered equivalent to spheres
(Chandrasekhar; 1960) with a mean diameter
D ,..., 25 µm and therefore the perimeter to
waveJength ratio (7T D/X) varies between 1.7
and 34. The lower limit, achieved at the long
wavelength end of the spectrum is still larger
than the onset for Rayleigh scattering. On the
other hand, for values of (tr /DX) > 10 the
interaction may be simply described as a nonselective reflection and difraction process.
The range, which overlaps most of the emission
curve of a black body at 300 K (fig. 1) falls
within the scope of Mie scattering theozy (van
de Hulst, 1957).
Claramente, este fen,
delar adecuadamente
pianos macrosc6picos
luz sufre reflexiones 1
{ndice de refracci6n n .
valor constante de n = 1
un modelo tal predecir
misi6n constantes, a dff
Procederemos ahor~
pueden derivar cuantitw
des tennicas a partir de
cedentes. Es preciso enf:
que siguen tienen com,
tal confirmar el meca11
de calor mas que prop,
calculo.
La ecuaci6n de transfere;
La ecuaci6n de tran~
si6n de la ley de Beer q
ci6n de la emisi6n espo
hacia adelante por el mr
Esto es particularmente
6pticamente densos en
incidente se atenua casi
reunimos brevemente la
Un tratamiento complete
Siegel y Howell (1972).
La intensidad local se .
absorbida y dispersada y
si6n espontanea y la <lisp
recci6n considerada. Para
ca elastica queda:
1.0
30
y
OJ
u
c
20
co
.0
'-
iii
.0
co
E
u
~
0.5
T=300 K
· donde a es el albedo y K
defmimos la funci6n fuc
de los terminos positivo~.
derecha, (1) se puede escr
3000
2000
1500
1000
500
Fig. 1.- Absorbancia vs. numero de onda para una hoja de poliestireno de 0,4 mm de espesor (ordenada iz·
quierda). Potencia emisiva de un cuerpo negro vs. n(1mero de onda (ordenada derecha). (Absorbance
vs. wavenumber for 0.4 mm thick polystyrene sheet (left ordinate). Blackbody emissive power vs.
wavenumber (right ordinate)).
184
*
Se puede obt!)ner a partir
rencia producidas por un
liestireno de 50 µm de e
hart, 1974).
VALENTIN T. AMOREBIETA, AGUSTIN J, COLUSSI
Lat. am. j. heat mass. transf.
ion
radiation heat transfer
ion impinging upon a layer
1am is partly removed by
1 part redirected by scat1e discrete features of the
1 correspond to molecular
'styrene. However, most of
deed removed by scattering,
te inverse dependence of the
ound with A.. A picture of
tniform polydisperse arrange.
oriented flat prisms, the cell
dimensions of 50 X 50 X 4
rith the above observations.
~ar scattering particles can
idered equivalent to spheres
~60) with a mean diameter
therefore the perimeter to
:rr D(A.) varies between 1.7
· limit, achieved at the long
· the spectrum is still larger
Rayleigh scattering. On the
1.lues of (rr /Df...) ;;;.. 10 the
: simply described as a non·
1 and difraction process.
1verlaps most of the emission
1ody at 300 K (fig. 1) falls
f Mie scattering theory (van
Claramente, este fen6meno no se puede mo~
delar adecuadamente por una red regular de
pianos macrosc6picos paralelos en los que la
luz sufre reflexiones multiples. Dado que el
fndice de refracci6n n de poliestireno tiene un
valor constante de n = 1,60 entre 2 ,5 y 5 0 µ.m *,
un modelo tal predeciria reflectividad y trans·
misi6n constantes, a.diferencia de lo observado.
Procederemos ahora a mostrar c6mo se
pueden derivar cuantitativamente conductividades termicas a partir de las observaciones precedentes. Es preciso enfatizar que las secciones
que siguen tienen como prop6sito fundamental confirmar el mecanismo de transferencia
de calor mas que proporcionar una rutina de
calculo.
La ecuaci6n de transferencia
Clearly, this phenomenon can not be ade·
quately modelled by a regular array of macroscopic parallel planes in which light undergoes
multiple reflections. Since the refractive index
n of polystyrene has a constant value· of n =
1.60 between 2.5 and 50 µm*, such a model
would predict wavelength independent reflectivity and transmission, at variance with observations.
We will proceed now to show how to quantitatively derive overall thermal conductivities
from the above observations. We wish to emphasize that the main thrust of the following
sections is to confirm the basic mechanism of
heat flow rather than to provide a calculational
routine.
The equation of transfer
La ecuaci6n de transferencia es una extenThe equation of transfer is an extension of
sion de la ley de Beer que incluye la contrlbu- Beer's· law to include the contribution of
ci6n de la emisi6n espontanea y la dispersion . spontaneous emission and forward scattering
hacia adelante por el medio a lo largo del haz. by the medium into the beam path. This is
Esto es particularmente importante en medios particularly important for optically dense
6pticamente densos en los cuales la radiaci6n media in which the incident radiation is almost
incidente se atemia casi completamente. Aqu{ completely attenuated. A brief survey of the
reunimos brevemente las expresiones basicas. basic expressions will be given here (Siegel and
Un tratamiento completo se puede encontrar en Howell, 1972).
Siegel y Howell (1972).
The local intensity ir.. (x) will be attenuated
La intensidad local se atenua por la radiaci6n
absorbida y dispersada y se refuerza por la emi· by radiation absorbed and scattered out and
si6n espontanea y la dispersi6n dirigida en la di· will be enhanced by spontaneous emission and
recci6n considerada. Para la dispersi6n isotr6pi- radiation scattered into the direction being
considered. For elastic isotropic scattering:
ca elastica queda:
ddxi'A
30
. + ar,. -.
= - ( a'A + a'A) l"A. + a'A l"Ab
l"As
y
20
E
u
dir.. = - lr,.
. +·(1 -dK'A.
i.
. + a: a:) lr,.b
l"A.s. •
(1)
donde a: es el albedo y " la densidad 6ptica. Si
definimos la funci6n fuente Ii\. como la suma
de los terminos positivos en el miembro de la
derecha, (1) se puede escribir asi:
where a:= a"Af(ar.. + ar._) and Ki\.~ (ai\. + ai\.)x.
Defining the source function Ii\. as the sum of
the positive terms in the RHS, (1) can be
written as:
*
*
500
),4 mm de espesor (ordenada izordenada derecha). (Absorbance
1. Blackbody emissive power vs.
Se puede obtener a partir de las bandas de interferencia producidas por un film transparente de poliestireno de SO µm de espesor (Hannah y Swinehart, 1974).
n can be obtained from the evenly spaced interference fringe pattern produced by a clear polystyrene film SO µm thick (Hannah and Swinehart,
1974).
185
Lat. am. j. heat mass. transf.
Rev. latinoam. transf. cal. mat.
(1')
Integration of (1 ') in the interval 0 :s;;; x :s;;; Q,
yields:
La integraci6n de (1') en el intervalo 0 :s;;; x
:s;;; ,Q,lleva a:
(2)
where KA= KA (Ji,) and K~ =KA (x).
Clearly, the intensity at optical depth KA is
composed of two terms. The first is the attenuated incident radiation arriving at x = JI,
and the second is the intensity resulting from
emission and scattering in the KA direction by
all elements along the path and reduced by exponential attenuation between the point of
emission K ~ and KA . Notice that the integral in
donde KA= KA (.Q,) Y K~ =KA (x).
Claramente, la intensidad a la densidad 6ptica KA se compone de dos terminos. El primero
es la radiaci6n incidente atenuada que llega a
x = JI, y el segundo es la intensidad que resulta
de la emisi6n y la redispersi6n en la direcci6n
KA por todos los elementos a lo largo del camino 6ptico y reducidos por atenuaci6n exponencial entre el punto de emisi6n K~ y KA. N6tese
que la integral en (2) se puede escribir asimismo
como
(2) can also be written as
J;A IA (KV exp (- KV d K~ tornado el
El coeficiente media efect
La transferencia de rac
en medios 6pticamente (:
problema formidable, dad
espectral de la radiaci6n ii
to tiene un caracter local.
terial gris la ecuaci6n (1) sc
Para una capa unidime
radiante requiere ademas c
dispersada que incide en c
asBT4 Irr y, por consiguien
la ecuaci6n (4) es directa:
i(Ji,) =
IA (KV exp
0
origen en KA. Cuando la (mica fuente significativa de radiaci6n es la que se origina en el haz incidente, como sucede en el registro de un espectro de una muestra delgada y fr{a (fig. 1),
(2) se reduce a la ley de Beer.
Para poder derivar el flujo neto de energ{a en
el caso mas simple de una capa unidimensional
entre dos placas grises infinitas y paralelas a T 1
y T2 separadas por la distancia JI, es necesario
escribir la ecuaci6n de transferencia (2) para
los caminos 1 -+ 2 y 2 -+ 1, integrarlas sobre 'A
y restarlas una de otra. En general, uno debe
obtener primero la distribuci6n estacionaria de
temperatura dentro de la capa ya que la emisi·
vidad del cuerpo negro es una funci6n de T. En
este caso el albedo es pnicticamente uno y las
propiedades 6pticas son practicamente independientes de la temperatura de modo que
h se desacopla de T (KV. Sin embargo, se puede demostrar que el formalismo se preserva para
todos los valores de ex, es decir desde absorci6n
pura a dispersi6n pura. Para una capa gris
KA = K y la soluci6n adopta una expresi6n
simple:
.
Jf'"A
\
(-KV dK~ by taking the origin at KA. When
the only significant intensity source is that
arising from the incident beam as in recording
the spectrum of a cold thin sample (fig.1),(2)
reduces to Beer's law.
De acuerdo a la ecuaci6r
a la intensidad direccional
mento (x, x + dx) es:
In order to derive the net energy flux in the
simplest case of a one dimensional layer conta·
ined between two infinite parallel gray plates
at T 1 and T2 separated by the distance JI,, it is
necessary to write down the transfer equations
(2) for the paths 1 -+ 2 and 2 -+ 1, integrate
them over 'A and substract one from the other,
In general, one must first obta)n the steady
state temperature distribution within the layer
as iAb, the blackbody emissivity, is a function
of T. In this case since the albedo ex ,.,, 1 and
the optical properties are nearly independent of
temperature, the source function IA becomes
decoupled from T (KV. However, it can be
shown that the formalism is preserved for all
values of ex, i.e. from pure absorption (ex= 0)
to pure scattering (ex = 1). For a gray layer
KA = (aA + aA) JI, = K and the solution takes a
simple expression:
Un coeficiente efectivc
homogeneo, isotermico qu.
preservar la forma de (6):
asB (Ti - Ti) '11
di (Q,)
=ib (x) (a+ a)e exr
Integrando los segundos
nos de (7) con respecto ax (1
- ib [ 1 -
exp {- 1
. A partir de (7) y (8) obt<
una expresi6n para el coeficie
(a+a)e(1
= 1 + '11 (€11 +s21 - 2)
donde '11 (K) es una funci6n integral que ha sido where w (1<)
qR
tabulada. Varia entre w (0,1) = 0,916 y
= 1,333 (1,421 +Kt1 paraK>1.
w(K)
is an integral function which has
been tabulated. It varies between '11 (0.1) ==
1
0916 and '11(K)=1.333 (1.421 + Kt for
K > 1. (Siegel and Howell, 1972; Heaslett
and Warming, 1965).
186
Esta representa una exten
persores del coeficiente de
Lat. am. j. heat mass. transf.
(l')
(1 ') in the interval 0 is;;; x is;;; JI,
(2)
~)and K~
1tensity at optical depth K-,,, is
o teims. The first is the att radiation arriving at x = JI,
s the intensity resulting from
ttering in the K-,,, direction by
~ the path and reduced by exation between the point of
"-,,, . Notice that the integral in
f:"" h
El coeficiente media efectivo
The effective mean coefficient
La transferencia de radiaci6n policromatica
en medios 6pticamente densos representa un
problema formidable, dado que la distribuci6n
espectral de la radiaci6n incidente en cada punto tiene un caracter local. En el caso de un material gris la ecuaci6n (1) se transforma en:
Polychromatic radiation transfer in optically
thick media represents a formidable problem
since the spectral distribution of incident radiation at each point has a local character. In the
case of a gray material a-,,, =a and a-,,, = a for
all A. and (1) transforms into:
-di = - i + (1 -
= K-,,, (x).
written as
VALENTIN T. AMOREBIETA, AGUSTIN J. COLUSSI
dK
Para una capa unidimensional, el equilibrio
radiante requiere ademas que la radiaci6n total
dispersada que incide en cada punto Ts = ib =
asB T4 /rr y, por consiguiente, la integraci6n de
la ecuaci6n ( 4) es directa:
i(.R.)=ib(O)exp(-K)+
(KV exp
De acuerdo a la ecuaci6n (5) la contribuci6n
a la intensidad direccional i (JI,) desde un elemento (x, x + dx) es:
rive the net energy flux in the
one dimensional layer conta·
'O infinite parallel gray plates
1arated by the distance JI, , it is
e down the transfer equations
1 1 ~ 2 and 2 ~ 1, integrate
substract one from the other,
must first obt~in the steady
) distribution within the layer
body emissivity, is a function
e since the albedo ex "" 1 and
rties are nearly independent of
source function 1-,,, becomes
T (KV. However, it can be
formalism is preserved for all
from pure absorption (ex= 0)
1g (ex = 1). For a gray layer
Q, = K and the solution takes a
Un coeficiente efectivo para un material
homogeneo, isotermico que no sea gris debe
preservar la forma de ( 6):
i
(4)
•
For a one dimensional layer, radiative equilibrium also requires that the total incident
scattered radiation Ts = ib = asB T 4 /~ and
therefore integration of ( 4) becomes straightforward:
J:
:aking the origin at K-,,,. When
:ant intensity source is that
incident beam as in recording
i cold thin sample (fig.1),(2)
law.
di(.R.)
ex) ib +ex i 8
ib(K*)exp(-K*)dK*.
According to (5) the contribution to the directional intensity i (JI,) from an element at
(x, x + dx) is:
= ib (x) (a+ a) exp [- K (x)] dx.
Integrando los segundos y terceros tenni·
nos de (7) con respecto ax donde 0 hasta JI, da:
- ib [ 1 - exp {- (a+ a)e JI,}]
=[
J:
A partir de (7) y (8) obtenemos finalmente
una expresi6n para el coeficiente efectivo:
(a+ a)e (JI,)= [
(6)
An effective coefficient for a nongray, homogeneous, isothermal material (i.e. a and a
independent of x) must preserve the form of
(6):
=):
di (.R.) = ib (x) (a+ a)e exp [-(a+ a)e x] dx
(5)
i"Ab (a+ ah exp [-(a+ a)A x] dx d'A. (7)
Integrating the second and third terms of
(7) with respect to x from 0 to JI, gives:
i"Ab exp - {(a + ah JI,} d A]- ib .
(8)
From (7) and (8) we finally obtain an expression for the effective coefficient:
~: i-,,,b (a+ a)-,,, exp {-(a+ ah JI,} dA.] X
1
n integral function which has
[t varies between '11 (0 .1) ==
1
I = 1.333 (1.421 + Kt
for
and Howell, 1972; Heaslett
55).
[~:i-,,,bexp{-(a+a)A.R.}dA.]- •
Esta representa una extension a medios dispersores del coeficiente de absorci6n medio
(9)
This represents an extension to scattering
media of the so called Patch's effective mean
187
Rev, latinoam. transf. cal. mat.
Lat. am, j. heat mass. transf,
· efectivo de Patch. El coeficiente medio efecti·
vo es ulia aproximaci6n util para materiales
no grises y que ha sido probado para medio no
dispersores solamente. Sin embargo, cabe se·
nalar que la ecuaci6n generalizada de transfe·
rencia (l ') incluyendo absorci6n, emisi6n y
dispersi6n retiene la misma forma en el caso de
absorci6n, emisi6n y dispersi6n, retiene la misma forma en el caso de absorci6n y emisi6n
puras y, por lo tanto, las aproximaciones matematicas a las soluciones se aplicaran en ambos
casos.
absorption coefficient. The effective mean
coefficient is an useful approximation for
nongray materials that has only been tested
for nonscattering media. However, it should
be pointed out that the generalized equation of
transfer (1 ') including absorption, emission and
scattering retains the same form in the case of
pure absorption and emission and therefore
many of the mathematical approaches to solutions will apply in both cases. (Patch, 1967).
La conductividad termica aparente
de una espuma
The apparent thermal conductivity of a foam
Alrededor de dos tercios de la fase s6lida
yacen paralelas a la direcci6n de flujo. Se pueden demostrar que la fracci6n de area transversal <fJ cubierta por poliestireno esta dada aproximadamente por
About two thirds of the solid phase lie along
the direction of heat flow, It can be shown that
the fraction of transversal area <fJ covered by
polystyrene is approximately given by:
En este caso con Pf= 19,8 Kg m- 3 , Pg=
1,189 Kg m- 3 y Ps = 1052,5 Kg m- 3 , </J =
0,0118. La· fracci6n remanente (1 - <P) =
0,9882 esta ocupada por aire pero sobre un camino levemente mas corto i (1 - 0,5 r/>). El
flujo de calor a traves de todo el material se
puede calcular por la ecuaci6n (11):
In this case with Pf= 19.8 Kg m~ 3 , Pg=
1.189 Kg :in- 3 and Ps = 10525 Kg m- 3 4>
0.0118. The remainder ( 1 - q,) = 0 .9882 ·
occupied by air but over a slightly shorter pa
length i ( 1 - 0 5 q,). The heat flow throu
the entire material can then be calculated b
(11):
bajo las suposiciones de conducci6n paralela
por las fases s6lidas y gaseosas y de flujo de ra·
diaci6n desacoplado. A partir de (11) la con·
ductividad tennica aparente o experimental ka
se puede calcular mediante (12):
under the assumptions of parallel conductio
by solid and gas phases and uncoupled radiatio
flow. From (11) the experimental or appare
thennal conductivity ka can be derived (12):
Con los coeficientes de extinci6n de tabla 1,
it..b a 300 K a partir de tablas de funciones de
cuerpo negro se obtiene por integraci6n numerica de (9) para i = 0,03 m: (a + a)e = 3,34
X 10 2 tj:l- 1 , lo que conduce a una densidad 6ptica efectiva Ke = 10,02 y '11 (Ke)= 0,1165. Suponiendo que las emisividades hemisfericas del
acero oxidado con que fueron fabricadas las
With the extinction coefficients of table 1
and it..b at 300 K from tables of blackb~d
functions we obtain by numerical integratiop. o
(9) for i = 0.03 m:(a + a)e = 3.34 X 102 m- 1
which leads to an effective optical depth Ke
10.02 and '11 (Ke)= 0.1165. Assuming fort
hemispherical emissivities of the oxidized ste
plates employed in the determination of ka
188
placas empleadas en la dt
valor de E 1
E2 = 0,8
se puede calcular a partir
m - 2 • Finalmente, con el 1
amorfo k 8 = 1,107 X IC
valor para aire seco kg =
K - 1 calculamo s a partir
10- 2 W m- 1 K- 1 en exc1
valor medido. N6tese qut
radiaci6n equivale a un 4
neto en estas condicione
sado en las propiedades
cuenta de las conductivi1
vadas y provee una met;,
ras investigaciones en este
=
Nomenclatura
coeficiente de absorci6n
dllimetro de particula
intensidad de radiaci6n d
gro
intensidad promedio salie1
funci6n fuente
conductividad termica
camino 6ptico
indice de refracci6n
flujo de energ{a
temperatura absoluta
coordenada en la direcciz
capa plana
dilimetro de celda gaseosa
espesor de pared
Letras griegas
albedo
emisividad
densidad 6ptica
longitud de onda
densidad
coeficiente de dispersi6n
constante de Stefan-Boltz1
fracci6n de area transversa
flujo adimensional de ener
Sub indices
aparente
cuerpo negro
efectiva
espuma
VALENTIN T. AMOREBIETA, AGUSTIN ,J. COLUSSI
Lat. am. j. heat mass. transf,
ifficient. The effective mean
an useful approximation for
ials that has only been tested
ng media. However, it should
that the generalized equation of
:luding absorption, emission and
ris the same form in the case of
n and emission and therefore
1athematical approaches to solu.
y in both cases. (Patch, 1967).
iermal conductivity of a foam
:hirds of the solid phase lie along
f heat flow. It can be shown that
0
transversal area </; covered by
.pproximately given by:
with Pf= 19.8 Kg m~ 3 , Pg
and Ps = 10525 Kg m- 3 .<fl
~mainder (1 - </;) = 0.9882 ·
r but over a slightly shorter pa
05 </;). The heat flow throu
.erial can then be calculated b
1mptions of parallel conducti
s phases and uncoupled radiati
1) the experimental or appare
~tivity ka can be derived (12):
:tinction coefficients of table
O K from tables of blackb~d
btain by numerical integratiop.
2
13 m:(a + a)e = 3.34 X 10 m' an effective optical depth Ke
:Ke) = 0.1165. Assuming fort
emissivities of the oxidized st
~d in the determination of ka
=
e:2 = 0 .8, the radiation heat flux
placas empleadas en la determinaci6n de ka un value of e: 1
valor de e: 1 "= e:2 = 0,8, el flujo de radiaci6n can be calculated from (3): CtR = 14.88 W m-2 •
se puede calcular a partir de (3): QR = 14,88 W Finally, with the value for amorphous polysm- 2 • Finahnente, con el valor para poliestireno tyrene ks= 1.107 X 10- 1 W m-1 K-1 and the
amorfo ks= 1,107 X 10- 1 W m- 1 K- 1 y el value for dry air kg= 250 X 10-2 W m-1 K-1
valor para aire seco kg= 2,50 X 10-2 W m- 1 we calculate from (12) ka = 4.84 X 10- 2 W
K- 1 calculamos a partir de (12) ka = 4,84 X m- 1 K- 1 in excellent ,agreement with the
10- 2 W m- 1 K- 1 en excelente acuerdo con el measured value. Notice that radiation transfer
valor medido. N6tese que la transferencia por amounts to about 48% of the net heat flow
radiaci6n equivale a un 48 % del flujo de calor under these conditions. This approach, based
neto en estas condiciones. Este enfoque ba- on the actual properties of the material is able
sado en las propiedades reales del material da to account for the observed thermal conductivicuenta de las conductividades termicas obser- .ties and provides a definite goal for further
vadas y provee una meta definida para futu- research in this field.
ras investigaciones en este tema.
Nomenclatura
Nomenclature
a
coeficiente de absorci6n
diametro de particula
intensidad de radiaci6n de un cuerpo negro
intensidad promedio saliente
funci6n fuente
conductividad termica
camino 6ptico
indice de refracci6n
flujo de energ{a
temperatura absoluta
coordenada en la direcci6n paralela a la
capa plana
dilimetro de celda gaseosa
espesor de pared
Xs
Letras griegas
Greek letters
albedo
emisividad
densidad 6ptica
longitud de onda
densidad
coeficiente de dispersion
constante de Stefan-Boltzmann
fracci6n de area transversal
flujo adimensional de energia
ex
e:
Sub indices
aparente
cuerpo negro
efectiva
espuma
D
i
I
k
JI,
n
q
T
x
Xg
"
;\
p
a
asB
</;
'11
absorption coefficient
particle diameter
radiation intensity of a blackbody
average outgoing intensity
source function
thermal conductivity
path length
refractive index
energy flux
absolute temperature
coordinate direction parallel to plane
layer
gas cell diameter
wall thickness
albedo
emissivity
optical depth
wayelength
density
scattering coefficient
Stefan-Boltzmann constant
fraction of transversal area
dimensionless energy flux
Subscripts
a
apparent
b
e
f
189
blackbody
effective
foam
Rev. latinoam. transf. cal. mat.
gas
racliante
dispersor, dispersado o s6lido
espectral
Lat. am. j. heat mass. transf.
g
R
s
A.
Rev. latinoam, transf. cal. mat
gas
radiant
scattered or scattering or solid
spectrally dependent
REVIEW PA PERS
References
Referencias
Chandrasekhar, S.: "Radiative Transfer", Dover, New York (1960).
Chem. Eng. News, June 9, 33 (1980).
Eckert, E. R. G. and Drake, R.H.: "Analysis of Heat and Mass Transfer" Mc Graw Hjll,New York (1972).
Hannah, R. W. and Swinehart, J. S.: "Experiments in Techniques of Infrared Spectroscopy", Perkin Elmer,
Norwalk, Conn. (1974).
Heaslett, M. A. and Warming, R. F.: "Radiative Transport and Wall Temperature Slip in an Absorbing Planar
Medium", Int. J. Heat Mass Transfer, 8: 979, (1965).
Marciano, J. H., Rojas, A. J. and Williams, R. J. J.: "A Theoretical Model for the Thermal Conductivity of Plastic Foams", Europ. J. Cellular Plastics 3: 102, (1980).
Patch, R. W.: "Effective Absorption Coefficients for Radiant Energy Transport in Nongrey, Nonscattering
Gases", J. Quant. Spectrosc. Radiat. Transfer, 7: 611, (1967).
Progelhof, R. G. and Throne, J. L.: "Cooling of Structural Foams" J. Cellular Plastics, 11: 152, (1975).
Progelhof, R. C., Throne, J. L. and Ruetsch, R. R.: "Methods for Predicting the Thermal Conductivity of Composite Systems: A Review'', Polym. Eng. Science, 16: 615, (1976).
Siegel, R. and Howell, J. R.: 'Thermal Radiation Heat Transfer" Mc Graw Hill, New York, chapters 14 and 20.
(1972).
Van de Hulst, H. C.: "Light Scattering by Small Particles", Wiley, New York (1967).
Recibido: Junio 22, 1982
Aceptado: Agosto 6, 1982
Received: June 22, 1982
Accepted; August 6, 1982
NON-CATALYTIC
TO COM!
INTEc
Abstract
The main models existing i
Using the criterion of gas acct
place are classified. The analysi
The additional complexity
is discussed, The paper particu
carbon particle. It reviews the r
I. Introduction
Non-catalytic gas-solid 1
Regeneration of coked cat
are some of their applicatio1
The successful design 01
chemical processes and trar
ous heterogeneous and hon
the gaseous film surroundir:
some anomalous s\tuations
For an adequate mathe1
ferential equations with no
situation thus established r
system of equations under :
frequently complicated by t
This review work deals
Using the criterion of acces
two main groups: inaccessil
porous structure is modelled
Those models considerin
quently examined. Accardi
* ResearcH fellow of the Nati'
** Institute of Technological L
and CONICET.
190