Cálculo con aplicaciones en Biolog´ıa

Cálculo con aplicaciones en Biologı́a
Homero G. Dı́az Marı́n
2
Contenido
1 El concepto de función
1.1 Funciones . . . . . . . . . . . . . . . . . . . . . . . . . .
1.2 Funciones lineales . . . . . . . . . . . . . . . . . . . . . .
1.3 Funciones crecientes y decrecientes . . . . . . . . . . . .
1.4 Funciones exponenciales . . . . . . . . . . . . . . . . . .
1.5 La función exponencial ex . . . . . . . . . . . . . . . . .
1.5.1 Crecimiento exponencial continuo de poblaciones
1.5.2 El logaritmo natural y tiempo de duplicación . .
1.5.3 Decaimiento radioactivo . . . . . . . . . . . . . .
1.5.4 Fechamiento de minerales y fósiles . . . . . . . .
1.6 Ejercicios de repaso . . . . . . . . . . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
5
5
9
12
15
20
20
23
25
26
27
2 La Derivada
2.1 Razón media de cambio . . . . . . . .
2.2 Razón instantánea de cambio . . . . .
2.3 Derivación de funciones polinomiales .
2.4 Derivación de funciones exponenciales
2.5 Problemas de máximos y mı́nimos . .
2.6 Ejercicios de repaso . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
31
31
32
35
39
41
43
3 La Integral
3.1 Integral Definida: Areas bajo la gráfica .
3.2 Integral Indefinida: Antiderivada . . . .
3.3 Cálculo de áreas usando integrales . . .
3.4 Cálculo de probabilidades . . . . . . . .
3.5 Ejercicios de repaso . . . . . . . . . . . .
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
.
49
49
53
56
57
64
3
4
Capı́tulo 1
El concepto de función
1.1
Funciones
El concepto de función es uno de los más importantes ya que nos permite expresar la dependencia
entre dos cantidades. En lenguaje cotidiano decimos por ejemplo: ”el precio de un automóvil
seminuevo está en función de su modelo”, ”el número de peces en un lago está en función de sus
niveles de contaminación”, ”el nivel de riqueza material de un paı́s es función de su PIB per capita”.
Estas frases expresan la idea de que al conocer un factor se puede determinar completamente al
otro. Para estudios de tipo cuantitativo consideramos que ambos factores son cantidades que toman
valores numéricos. Es decir, hablaremos de la dependencia de dos cantidades que toman valores en
el conjunto de los números reales R.
Definición. Una función f es una regla que a todo valor numérico x dentro de un conjunto D ⊂ R,
le asigna un único valor numérico que se denota como f (x). El conjunto D se llama dominio de la
función, x es el argumento o variable independiente y al valor y = f (x) se le llama variable
dependiente y se lee “el valor de f evaluada en x”.
Una función puede pensarse también como un procedimiento bien determinado que dado un
número x lo transforma en otro número f (x). Dicho procedimiento se puede especificar de varias
maneras: o bien mediante una fórmula o expresión analı́tica, o bien mediante una tabla, o bien
mediante una gráfica.
Una fórmula es una igualdad en la que de un lado muestra la función, f (x), mientras que del
otro lado, se indican las operaciones que es necesario hacer con x para obtener el valor de f (x).
Ejemplo. Una población de bacterias inicialmente es de 1000 colonias y se incrementa en 20 colonias
cada hora, expresar el número de colonias N como una función de x, las horas transcurridas desde
el inicio de la observación.
Este ejemplo ilustra como el lenguaje algebraico puede ser de gran utilidad para expresar una
función mediante una fórmula. Ası́ podemos traducir la frase ”se incrementa en 20 colonias cada
hora” adicionando el término 20x y obtenemos la fórmula
N (x) = 1000 + 20x
La función queda completamente especificada con esta fórmula.
Una función puede expresarse también como una tabla, es decir una colección de valores de x
que forman parejas con sus respectivos valores f (x) asignados mediante la función.
Ejemplo. Se midió la estatura (en cm) de un niño cada cumpleaños y se obtuvieron las siguientes
mediciones
5
x (años)
f(x) (cm)
1
55
2
67
3
81
4
115
5
127
6
135
7
140
Dada una fórmula para una función siempre es posible construir una tabla que cualesquiera
valores en x le asigne los valores correspondientes de la funcin.
Es claro que una fórmula contiene más información que una tabla, ya que una tabla sólo contiene
una colección finita de valores de una función, mientras que una fórmula contiene una infinidad de
valores para la función. En el ejemplo anterior, si tuviésemos una fórmula podrı́amos determinar la
estatura del niño en cualquier instante y no solamente cada cumpleaños. Por supuesto que en este
momento nos parece difı́cil ”adivinar” cul es la fórmula que describa la talla como función del peso
del niño.
Hay situaciones de la vida cotidiana en las que a partir de mediciones y una tabla, es posible
”adivinar” una fórmula o una ”ley” que predice dichas mediciones. Precisamente el cálculo surgió
como una necesidad de darle poder predictivo a la ciencia, al permitirle elaborar estas leyes en
términos de funciones.
Ejemplo. Galileo observó que los cuerpos que caı́an libremente describı́an movimientos similares.
Por ejemplo al dejar caer una piedra desde la torre de Pisa, observó que la distancia recorrida, h
(en metros) por la piedra, se podı́a describir como función del tiempo transcurrido, t (en segundos),
desde que se habı́a dejado caer. Además observó que no importaba la masa de la piedra, es decir,
las mediciones eran las mismas, con piedras de masas diferentes:
t (s)
h(t) (m)
0
0
1
4.9
2
19.62
3
44.14
4
78.48
5
122.625
Después, Galileo, asumió que el movimiento debı́a ser uniformemente acelerado, y a partir de esta
hipótesis y algunas deducciones matemáticas llegó a la conclusión de que la altura h(t) debı́a tener
la siguiente fórmula que expresaba la distancia vertical recorrida como función del tiempo
h(t) = 4.905t2
Como los datos predichos por la fórmula concordaban con mucha precisión con las mediciones observadas, atribuimos a Galileo el “descubrimiento” de la “ley” de la caı́da libre.
Ası́ nació el concepto de ley de la naturaleza como un conjunto de hipótesis que mediante procedimientos matemáticos precisos predicen fenómenos contrastables con mediciones.
De la misma manera a como hizo Galileo, en muchos fenómenos biológicos es posible formular
hipótesis biológicas que permiten arribar a predicciones contrastables con la observación. A esta
herramienta predictiva se le denomina modelo matemático (determinista) del fenómeno en cuestión.
Decimos que una variable dependiente y es directamente proporcional (por brevedad usaremos tambin el trmino proporcional) a una variable independiente x, si la razón entre ambas es
constante; es decir, si y = kx, donde k se llama constante de proporcionalidad. Ası́ por ejemplo, si
el precio y (en pesos) de una bolsa de azúcar es proporcional al peso x (en kg), con constante de
proporcionalidad 18, quiere decir que por cada kilo de azúcar debemos pagar 18 pesos. Si el precio
es función del peso la función queda determinada por
y = f (x) = 18x.
Ejemplo. Los siguientes datos corresponden a la edad E en millones de años de rocas presentes en
una excavación. La variable independiente x corresponde a la profundidad de la que se extrajo la
roca.
Profundidad (m)
5 10 15 20
25
Edad (mill. años) 20 40 60 80 100
6
120
120
100
100
80
80
60
60
40
40
20
20
0
1
2
3
4
5
6
0
5
10
15
20
25
Figura 1.1: Algunos puntos de la gráfica de h(t) = 4.905t2
120
100
80
60
40
20
0
1
2
3
4
5
Figura 1.2: Gráfica de h(t) = 4.905t2
Notamos que la edad E es proporcional a la profundidad de la excavación x con constante de
proporcionalidad k = 4. Es decir, E = 4x o como función E(x) = 4x. Notamos además que k tiene
como unidades m/mill. años.
Definición. La representación gráfica de una función f (x) es el trazo en el plano cartesiano
que se obtiene al considerar todos los puntos de la forma (x, f (x)), tomando todos los posibles valores
x en el dominio D de la función.
En términos prácticos la representación gráfica (o simplemente gráfica) de una función se puede
esbozar o dibujar si se conoce una tabla con un número suficiente de evaluaciones de la función. En
tal caso tendremos una colección de puntos en el plano cartesiano y suponiendo la ”continuidad” de
la función podemos intercalar el trazo de la gráfica completa.
Ejemplo. Para trazar la gráfica de la función de caı́da libre h(t) = 4.905t2 en el lapso de tiempo de
0 a 5 segundos, utilizamos las evaluaciones de la siguiente tabla para esbozar la gráfica de la función
en el el intervalo [0, 5].
t (s)
h(t) (m)
0
0
1
4.9
2
19.62
3
44.14
4
78.48
5
122.62
con ello obtenemos una colección de puntos en el plano cartesiano:
Al considerar más evaluaciones intermedias (t=.2, .4, .6, etc.) se obtienen más puntos de la gráfica
y se puede esbozar la gráfica con más detalle. Al final la gráfica se esboza como un trazo continuo
que une todos los puntos calculados:
En muchas circunstancias se desconoce la fórmula de una función y solamente es posible trazar
algunos puntos.
7
250
200
150
100
50
0
2
4
6
8
10
12
Figura 1.3: Crecimiento de una planta de girasol
Ejemplo. Los siguientes datos corresponden a las mediciones de la altura de una planta de girasol,
cada semana
t (Semanas)
Altura (cm)
1
10
2
25
3
60
4
87
5
123
6
165
7
201
8
224
9
235
10
250
11
251
12
251.5
La gráfica correspondiente a estos datos consta de una curva quebrada que une los puntos señalados.
Como desconocemos la fórmula de la función que describe la altura h(t) de una planta de girasol
como función del tiempo t, no es posible trazar más puntos de la gráfica. Si quisiéramos introducir
más datos tendrı́amos que hacer más mediciones. En estos casos, para tener una idea de como serı́a
la gráfica unimos los puntos con segmentos rectilı́neos y obtenemos un trazo poligonal para la gráfica
de la función.
EJERCICIOS
1. La cantidad de aguacates (en toneladas) producidas en una huerta es proporcional, al número
de árboles en el huerto. Si el huerto consta de 255 árboles y produjo 145 toneladas.
(a) Calcula la constante de proporcionalidad. ¿Qué unidades tiene la constante de proporcionalidad?
(b) Expresa la producción P como función del número de árboles x.
(c) Elabora la tabla correspondiente para x = 0, 50, 100, 150, 200.
(d) Esboza la gráfica de P (x).
2. Los siguientes datos corresponden a la temperatura (en grados celsius) en el desierto del
Vizcaı́no durante un dı́a de invierno.
t hora
T Temperatura (o C)
0
2
4
-5
8
10
12
35
16
25
20
15
(a) Esboza la gráfica mediante una poligonal.
(b) ¿En qué momento aproximadamente se alcanza la temperatura máxima? ¿Y la mı́nima?
3. Los siguientes datos corresponden a observaciones del crecimiento de bacterias en un cultivo
de E. Coli llevados a cabo en el Instituto Pasteur del sur de India en 1910. Se mantuvieron
8
las bacterias a una temperatura constante de 37 Co y nutrientes de extracto de carne con sal.
t (hr)
0
0.5
1
2
3
4
5
6
P(t) (bacterias)
2,850
7,500
17,500
105,000
625,000
2,250,000
17,750,000
50,000,000
(a) Esboza la gráfica de la población P como función del tiempo t, con los datos proporcionados.
(b) ¿Cuál era la población de bacterias al inicio del experimento?
4. La función de costo, C(x), describe el costo de producción en (miles de pesos) en una granja
de truchas para producir x toneladas de trucha al año. Se determinó en un estudio que dicha
función tenı́a la forma
C(x) = −0.005x2 + 12.5x + 75.
(a) Evalúa el costo cada 250 tons., es decir en x = 0, 250, . . . , 1500
(b) Esboza la gráfica de la función costo C(x) en el intervalo [0, 1500].
(c) ¿Aproximadamente cuántas toneladas tienen el costo máximo? ¿Aproximadamente cuál
es el costo máximo?
1.2
Funciones lineales
Definición. Una función lineal es una función de la forma
f (x) = mx + b
donde m se llama pendiente y b se llama ordenada al origen.
Las funciones lineales son las funciones más sencillas que podemos encontrar. Su gráfica también
es muy sencilla.
Afirmación. La gráfica de una función lineal f (x) = mx + b es un recta que interseca al eje y en
el punto (0, b). Si θ es el ángulo que forma dicha recta con el eje x, entonces θ está determinado
por la pendiente m,
m = tan θ, θ = tan−1 m.
Se sigue de esta afirmación las siguiente observaciones
1. Si m = 0, entonces la gráfica es una recta es horizontal, es decir, paralela al eje x, además y
es la función constante y = b.
2. Si m > 0, entonces la gráfica es una recta que forma un ángulo θ agudo entre 0o y 90o con el
eje x
3. Si m < 0, entonces la gráfica es una recta que forma un ángulo θ obtuso entre 90o y 180o con
el eje x.
9
10
8
6
4
2
-1.0
-0.5
0.5
1.0
1.5
2.0
-2
Figura 1.4: Gráfica de y = 4.5x + 1.5
De esta manera, para trazar la gráfica de un función lineal cuando conocemos su fórmula lo único
que necesitamos es trazar dos puntos y después unirlos con una recta (una recta está completamente
determinada por dos puntos).
Ejemplo. Si y es una función lineal de x con ordenada al origen 1.5 y pendiente 4.5; entonces la
relación correspondiente se pede expresar como y = 4.5x + 1.5. Su intersección con el eje y, es decir
con la recta x = 0, es el punto (0, 1.5). Su intersección con el eje x se puede obtener haciendo y = 0,
es decir x = −1.5/4.5 = −1/3. Ası́ la intersección con el eje x es el punto (−1/3, 0). Es posible
trazar la gráfica de la función trazando la recta que pasa por los puntos (0, 1.5), (−1/3, 0).
Ejemplo. Los siguientes valores corresponden a una función lineal, determinar de qué función lineal
se trata.
x 3.5 4.2 0
y
-1
-2 4
Solución. Dado que sabemos que y es función lineal de x, entonces tenemos que determinar los valores
de la pendiente m y la ordenada al origen b en la ecuación y = mx + b. Basta considerar dos parejas
de valores para determinar la función; por ejemplo, al considerar las parejas (3.5, −1), (4.2, −2) y
sustituyendo en la ecuación de la recta, obtenemos
−1 = 3.5m + b
−2 = 4.2m + b
Este es un sistema de dos ecuaciones lineales con dos incógnitas m, b. Para resolverlo podemos usar
por ejemplo el método de suma o resta: Restamos la segunda ecuación de la primera y obtenemos
1 = −0.7m
De donde m = −1/0.7. Sustituyendo el valor de m en alguna de las dos ecuaciones, por ejemplo en
la primera, se obtiene b = −1 − 3.5(−1/0.7) = −1 + 5 = 4. Por lo tanto, la ecuación de la función
lineal que corresponde a la tabla de valores mencionada es
y = −10/7x + 4
Ejemplo. Una recta forma un ángulo de 30o con el eje x y pasa por el punto (1, 2). Determina la
ecuación de la recta y = mx + b.
√
Solución. En este caso la pendiente es m = tan 30o = 1/ 3, para determinar el valor de b
la ordenada al origen sustituimos m por 0.5, y la pareja (x, y) por (1, 2) en la ecuación de la recta
y = mx + b.
√
2 = (1)1/ 3 + b
√
√
√
de donde b = 2 − 1/ 3. Finalmente la ecuación de la recta es = (1/ 3)x + 2 √3−1
.
3
10
Los modelos lineales son muy sencillos y en algunas situaciones pueden describir algunos fenómenos
biológicos.
Ejemplo. En un cultivo de células gliales originalmente habı́a 1000 células; se observó posteriormente que el número de células presentes se incrementaba en 20 cada semana. Expresa el número
de células presentes, P (t), como función de t, el número de semanas transcurridas.
Solución. El modelo lineal que corresponde serı́a una ecuación de la forma
P (t) = mt + P0
donde la ordenada al origen es P0 , convenientemente es la población al inicio del experimento. La
pendiente m indica la porción de células que se incorporan por unidad de tiempo; en nuestro caso
m = 20 células/semana. De esta manera, la función lineal que expresa la población de células como
función del tiempo es
P (t) = 20t + 1000
Ejemplo. El número de oyameles presentes en una reserva, decrece de manera lineal por la tala
clandestina. Originalmente habı́a 2000 ejemplares y 6 meses después su número se habı́a reducido a
1850.
1. Encuentra la función lineal que describe el número de árboles presentes t meses después de
iniciadas las observaciones.
2. ¿En cuánto tiempo desaparecerán los oyameles de la zona?
Solución. Como se trata de una función lineal tenemos que emplear la siguiente expresión P (t) =
mt + P0 . Sabemos que originalmente (cuando t = 0) la población es P0 = 2000 oyameles. Para
conocer el valor de la pendiente m, sustituimos (t, P ) por (6, 1850), en la ecuación, obteniendo
1850 = 6m + 2000,
Despejando m, 6m = 1850 − 2000, m = −150/6 = −25. El valor negativo quiere decir que la
cantidad de oyameles está disminuyendo a una rapidez de 25 árboles por mes. Ası́ tenemos
P (t) = −25t + 2000
b) Para responder a la pregunta planteada, tomemos en cuenta de que si los oyameles desaparecen,
entonces P = 0, es decir,
0 = −25t + 2000
2000
= 80 meses.
t=
25
Lo que significa que si esta tendencia se mantiene, deben transcurrir 80 meses para que desaparezcan
por completo los oyameles.
EJERCICIOS
1. Encontrar la función lineal que proporciona los siguientes datos
x
2
3
y
-2.3
1.4
2. Una población de 2000 bacterias se coloca en un cultivo y se observa un crecimiento lineal
durante 4 dı́as. Al final de los cuatro dı́as la población era de 6250 células. Escribe la población
como función de los dı́as transcurridos. Esboza la gráfica en el intervalo [0, 4].
11
2000
1500
1000
500
20
40
60
80
Figura 1.5: Gráfica de P (t) = −25t + 2000
3. Durante el siglo XVII las ballenas del Atlántico Norte casi se extinguieron por a causa del
exterminio de la industria pesquera Europea. En un periodo de 50 años, la población descendió
de 25,000 ejemplares a sólo 20. Suponiendo una función lineal de decremento de la población.
(a) Determina la función que describe la población en relación del tiempo transcurrido en
años.
(b) ¿Aproximadamente cuántas ballenas desaparecı́an cada año durante ese periodo?
(c) ¿Después de cuánto tiempo la cantidad de ballenas se habı́a reducido a la mitad?
Aunque aún existen en nuestros dı́as las ballenas en el Atlántico Norte, éstas están condenadas a la extinción.
4. Al inicio del siglo XX en México se hablaban 106 lenguas. Al inicio del 2010, sólo se hablan
46. Suponiendo una función lineal, que expresa el número de lenguas que se hablan, P , como
función de los años, t, transcurridos desde 1900. ¿Encuentra P0 y m en la ecuación P = mt+P0 .
De seguir esa tendencia ¿En cuánto tiempo perderá México su diversidad cultural?
5. El precio de la gasolina es de $ 12.09 el litro. Durante un año, el precio se incrementará en 9
centavos cada fin de mes, a partir de enero.
(a) Escribir el precio P del litro de gasolina como función lineal de los t meses transcurridos
desde enero.
(b) ¿Cuál será el precio de la gasolina al finalizar junio?
(c) Hacer la gráfica de la función en el intervalo [0, 12].
(d) ¿En qué mes el precio de la gasolina será mayor a $ 13 el litro?
1.3
Funciones crecientes y decrecientes
Definición. Una función f (x) es creciente (resp. decreciente) en un intervalo α < x < β, si para
toda pareja α < x0 < x < β se cumple que f (x0 ) < f (x) (resp. f (x0 ) > f (x)).
En general es difı́cil determinar si una función es creciente o decreciente en un intervalo; ya que
es necesario comparar todas las parejas de puntos x0 < x. Dichas parejas son infinitas, ası́ que en
principio serı́a imposible concluir nuestra tarea.
También es posible entender el comportamiento creciente o decreciente de una función en términos
de sus incrementos o decrementos dentro de un intervalo.
12
Definición. El cambio o variación de una función f (x) definida en un intervalo a ≤ x ≤ b se
define como
∆f = f (b) − f (a).
Si ∆f > 0, decimos que se trata de un incremento. Si ∆f < 0 decimos que se trata de un
decremento.
Afirmación. f (x) es creciente (decreciente) en un intervalo α < x < β si f (x) tiene un incremento
(decremento) en todo subintervalo a ≤ x ≤ b, α < a < b < β.
También en términos de incrementos y decrementos no resulta muy práctica la definición de
función creciente en un intervalo ya que hay una infinidad de subintervalos a ≤ x ≤ b contenidos en
un intervalo α < x < β.
No obstante estas dificultades para determinar si una función es creciente o decreciente, para la
clase de funciones lineales es relativamente sencillo verificar si se trata de una función creciente o
decreciente.
Afirmación. Una función lineal f (x) = mx + b es creciente (resp. decreciente) en todo su dominio
si m > 0 (resp. m < 0).
En aquellas funciones que no son lineales una misma función puede tener comportamiento creciente o decreciente en intervalos distintos.
Ejemplo. Supongamos que P (t) es la población de células cancerosas en un cultivo sometido a
cierto fármaco. En un estudio se determinó que la ecuación que describı́a la población como función
de los dı́as transcurridos era
P (t) = −0.3t2 + 24t + 500
Observemos que ésta no es una función lineal. La población al inicio del experimento (t = 0) era de
P (0) = 500 células. Para realizar la tabla calculamos la población cada 10 dı́as y obtenemos
t dı́as
P(t) células
0
500
10
710
20
860
30
950
40
980
50
950
60
860
70
710
80
500
Al esbozar la gráfica parece que la función es creciente en el intervalo 0 < t < 40 y decreciente para
t > 40.
1000
800
600
400
200
20
40
60
80
100
Figura 1.6: Gráfica de P (t) = −0.3t2 + 24t + 500
Remarquemos que solamente hemos afirmado que ”parece” ser creciente en el intervalo 0 < t <
40, basándonos en algunas cuantas parejas de valores de la función. Nuestro argumento además es
13
sustentado por criterios gráficos. Sin embargo, tendrı́amos que argumentar de alguna manera que el
comportamiento creciente se mantiene para toda pareja (t0 , t), de números tales que 0 < t0 < t < 40,
no solo para los puntos que hemos considerado. Esta es una de las motivaciones por las que más
adelante introduciremos el concepto de derivada.
La totalidad de las células desaparecen cuando P = 0. Resolviendo para t tenemos
0 = −0.3t2 + 24t + 500
Empleamos la fórmula general para encontrar las raı́ces de un polinomio cuadrático ax2 + bx + c, la
cuál es
√
−b ± b2 − 4ac
x=
2a
En nuestro caso a = −0.3, b = 24, c = 500. Sustituyendo tenemos
√
−24± 242 −4(−0.3)(500)
t =
2(−.3)
el valor que hace sentido en este problema se obtiene tomando el signo “-” en la raı́z cuadrada;
t = 97.1548 por lo que aproximadamente después de 97 dı́as todas las células cancerosas han desaparecido.
Podemos resumir el comportamiento de la población en el ejemplo anterior como sigue:
• Primero la población ”parece” crecer hasta aproximadamente los 40 dı́as.
• La población ”parece” tener un valor ”máximo” de 980 células después de 40 dı́as.
• En seguida ”parece” que decrece hasta finalmente desaparecer después de aproximadamente
97 dı́as.
De este análisis podemos extraer la siguiente conclusión
Afirmación. Si f (x) es una función creciente (resp. decreciente) en α < x < x0 y decreciente
(resp. creciente) en x0 < x < β, y si además es una función continua; entonces f (x) tiene un valor
máximo (resp. mı́nimo) local en x0 . Es decir, f (x0 ) ≥ f (x) (resp. f (x0 ) ≤ f (x)), para todo
α < x < β.
La condición de que f (x) sea continua se refiere intuitivamente a que el trazo de su gráfica sea
continuo. Nosotros consideraremos siempre funciones continuas por lo que este tecnicismo no será
visto detallado. La denominación ”máximo local” se refiere a que la función adquiere un máximo
en un intervalo α < x < β que contiene a x0 , pudiendo tener otros máximos fuera de este intervalo.
EJERCICIOS
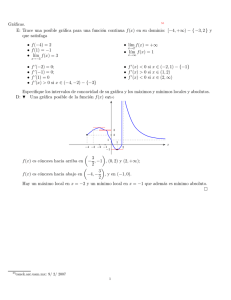
1. Suponiendo que una función tiene la gráfica indicada en la figura 1.8 señala aproximadamente
cuales son los intervalos en los que es creciente, decreciente y los valores de x donde alcanza
un máximo o mı́nimo local.
2. En cierto modelo, la tasa de crecimiento de la biomasa es f (x) y es función de la biomasa x
de un recurso natural. f (x) está dada por
x
f (x) = rx 1 −
K
donde r es la tasa intrı́nseca de crecimiento; K es el nivel de saturación. Para una población
de truchas K = 5000, r = 0.05.
14
6
4
2
2
4
6
8
10
-2
-4
-6
Figura 1.7: Una función con dos máximos locales y dos mı́nimos locales
8
0.25
6
0.20
4
0.15
2
2
0.10
4
6
8
10
-2
0.05
-4
-6
[h]
-4
-2
2
4
Figura 1.8:
(a) Esboza la gráfica de f (x) utilizando los valores x = 1000, 1500, . . . , 3500, 4000.
(b) ¿En qué intervalo de 1000 < x < 4000 es creciente la función f (x)? ¿dónde es decreciente?
(c) Para qué valor de x, f (x) alcanza un valor máximo? ¿Cuál es el valor máximo de f (x)?
(d) Para qué valores de x, la tasa de crecimiento f (x) es 0.
1.4
Funciones exponenciales
Una función exponencial de base a, a > 0, a 6= 1, es una función que tiene la forma
f (x) = abx .
También las funciones exponenciales tienen criterios muy sencillos para verificar si se trata de
funciones crecientes o decrecientes.
Afirmación. La función exponencial f (x) = abx , es creciente
1. Si a > 1, b > 0,
2. Si 0 < a < 1 y b < 0.
Es decreciente
15
y
12
10
8
6
4
2
-3
-2
-1
1
2
3
x
Figura 1.9: Gráficas de 0.5x , 1.5x , 0.5−2x , 0.52x
1. Si a > 1 y b < 0
2. Si 0 < a < 1 y b > 0.
Para ver como aparecen las funciones exponenciales en el estudio de poblaciones biológicas,
analicemos el siguiente ejemplo.
Ejemplo. Supongamos que un biólogo desea estudiar la reproducción de unas aves migratorias que
llegan a una reserva. Ss sabe que dichas aves tienen un sólo periodo de reproducción al año. Realiza
el conteo de la población al final del periodo de reproducción durante cinco años consecutivos. Se
obtienen los siguientes datos
t P (t) Incremento
0 2500
1 2550
50
2 2601
51
3 2653
52
4 2706
53
5 2760
54
6 2815
55
7 2872
57
Observa que la población no crece de manera lineal (¿Porqué?)
Sin embargo el patrón de crecimiento tiene la siguiente peculiaridad:
Incremento anual
≈ .02
Población al inicio del año
Es decir la tasa porcentual de crecimiento se mantiene más o menos constante y es de 0.02×100 = 2%.
t
0
1
2
3
4
5
6
7
P(t)
2500
2550
2601
2653
2706
2760
2815
2872
Incremento anual
Tasa porcentual de crecimiento
50
51
52
53
54
55
57
2
2
1.999
1.997
1.996
1.993
1.985
16
P
7000
6000
5000
4000
3000
2000
1000
0
10
20
30
40
50
t
Figura 1.10: Gráficas de P (t) = 2500(1.02)t con t entero
Este modelo se puede generalizar de la siguiente manera
Afirmación. Bajo ciertas condiciones es posible suponer que una población se incrementa en la
misma proporción o porcentaje cada periodo de reproducción. La ecuación que describe el crecimiento
(decrecimiento) de la población bajo estas circunstancias es
P (t) = P0 (1 + r)t para crecimiento
P (t) = P0 (1 − r)t para decrecimiento
Donde t son los periodos de reproducción transcurridos. P0 es la población inicial (cuando t = 0).
r es la tasa porcentual de crecimiento (decrecimiento) por periodo de reproducción.
Regresando a los datos del ejemplo anterior vemos como haciendo r = .02 y P0 = 2500 tenemos
el modelo exponencial P (t) = 2500(1.02)t . A continuación contrastamos los datos observados con
los datos predichos por el modelo.
t
0
1
2
3
4
5
6
7
Población
2500
2550
2601
2653
2706
2760
2815
2872
P(t)
2500
2550
2601
2653.02
2706.08
2760.202
2815.406
2871.714
Ejemplo. Una población de ballenas se reproduce una sola vez al año. Inicialmente hay 850
individuos y después de un año la población es de 857. Suponiendo un modelo a tasa porcentual
constante una vez cada año, P (t) = P0 (1 + r)t .
1. Determina el valor de la población inicial P0 y de la tasa porcentual de crecimiento r.
2. ¿Cuál será la población 10 años después de iniciadas las observaciones?
17
P
1200
1000
800
600
400
200
0
10
20
30
40
50
t
Figura 1.11: Gráfica de P (t) = 850(1 + .008235)t con t entero
Solución. Es claro que P0 = 850 (¿porqué?). Para determinar el valor de r, basta considerar la
proporción en la que se incrementó la población al cabo de un año.
r=
Incremento de la población
857 − 850
=
Población al inicio del periodo
850
r=
7
≈ .008235
850
El modelo exponencial es
t
7
P (t) = 850 1 +
,
850
basta sustituir t = 10.
10
7
P (10) = 850 1 +
≈ 923.
850
También puede estudiarse el decrecimiento de poblaciones con este modelo exponencial. En este
caso la ecuación que describe la población como función del tiempo es
P (t) = P0 (1 − r)t
donde r tiene ahora un signo menos que indica que se trata de una tasa de decrecimiento.
Ejemplo. Una población de monos araña en una región de la selva en Campeche disminuyó de 1320
ejemplares a 1200 ejemplares en 6 años. Suponiendo un modelo de decrecimiento a tasa porcentual
constante, P (t) = P0 (1 − r)t y un periodo de reproducción al año. Determina el valor de la tasa de
decrecimiento.
Solución. Debemos despejar r de la ecuación
P
(1 − r)t
=
=
1−r
=
r
=
18
P0 (1 − r)t
P
P0 1t
P
P0
1−
q
t
P
P0
P
1400
1200
1000
800
600
400
200
0
5
10
15
20
25
30
t
Figura 1.12: Gráfica de P (t) = 1320(1 − .01576)t con t entero
Sustituyendo P0 = 1320, t = 6 y P (6) = 1200, tenemos:
r
r =1−
6
1200
≈ .01576
1320
es decir una tasa porcentual constante de decrecimiento de 1.576%.
Observación. El despeje para r en el modelo de crecimiento P (t) = P0 (1 + r)t es
r
r=
t
P
− 1.
P0
en tanto que para el modelo de decrecimiento (como en el problema anterior)es
r
r =1−
t
P
.
P0
EJERCICIOS
1. Una población de golondrinas que arriba a una comunidad se incrementó de 5600 ejemplares
a 5630 al cabo de un año. Suponiendo un periodo de reproducción anual a tasa porcentual
anual constante. Determina dicha tasa r.
2. Durante la revolución mexicana la población en México disminuyó de 15 millones en 1910,
a 13.9 millones de habitantes en 1920. Suponiendo un modelo exponencial anual P (t) =
P0 (1 − r)t , donde t son los años transcurridos desde 1910 y P0 es la población de 1910 y r es
la tasa porcentual anual de decrecimiento.
(a) Determina la tasa porcentual anual de decrecimiento, r.
(b) Esboza la gráfica de la función usando t = 0, 1, 2, . . . , 10
3. El precio del gas se incrementara en 5 % mensual al final de cada mes a partir de enero. Si el
precio original del cilindro de gas es 285 pesos al 1 de enero. Escribe el precio del cilindro de
gas como función de los meses t transcurridos a partir del inicio del año. ¿Cuál será el precio
el 31 de julio?.
19
1.5
1.5.1
La función exponencial ex
Crecimiento exponencial continuo de poblaciones
Hemos visto que el modelo de crecimiento exponencial de una población P (t) = P0 (1 + r)t , supone
las siguientes hipótesis:
A) La población se reproduce con una tasa porcentual constante.
B) La población se incrementa por ”saltos”, es decir, sólo lo hace una vez por periodo de reproducción.
La hipótesis B es adecuada para describir el crecimiento de algunas poblaciones como las golondrinas, ballenas, para las cuales las escalas temporales pequeñas no son tan importantes. Por ejemplo,
para una población que se reproduce una sola vez al año, no nos interesa mucho saber cuál es la
población en escala de dı́as entre dos fechas de conteo sucesivas.
Sin embargo esta hipótesis resulta inadecuada y poco realista ya que en general la dinámica de
poblaciones tiene lugar de manera continua. En el tiempo los organismos nacen y mueren sin tener
una fecha especı́fica para hacerlo, por lo que el conteo de la población debe considerarse como un
fenómeno continuo en el tiempo que no se produce mediante saltos.
Por ejemplo en el estudio del crecimiento semanal de bacterias en un cultivo, no es posible suponer
que la población se incrementa sólo cada semana. Es más factible suponer que la población se está
incrementando de manera continua, instante a instante. En otras palabras, las escalas de tiempo
pequeñas (por ejemplo horas, minutos o segundos) resultan importantes para el bacteriólogo.
Ejemplo. Una población de 30000 bacterias en un cultivo se reproduce a tasa porcentual constante
de 5 % semanal. Calcula la población de bacterias transcurridas 2 semanas, suponiendo que se
reproducen una vez cada: a) Semana; b) Dı́a; c) Hora; d) Minuto; e) Segundo.
Solución. a) Sustituimos P0 = 30000, r = .05 y t = 2 en el modelo P (t) = P0 (1 + r)t ,
P (2) = 30000(1.05)2 = 33075
b) Suponiendo que las bacterias se reproducen una vez por dı́a, entonces la dinámica de la
población de bacterias difiere. Denotemos k = 7 el número de dı́as de la semana. Entonces dado
que la tasa porcentual r = 0.05 es semanal, debemos considerar una nueva tasa porcentual diaria,
a saber, r/k = .05/7. Además en 2 semanas debemos considerar kt = 7(2) = 14 periodos de
reproducción de donde, la población al final de las dos semanas serı́a
r kt
= 30000(1 + .05/7)14 ≈ 33143.
P = P0 1 +
k
Para los siguientes incisos podemos completar la siguiente tabla que muestra la evolución de la
población para los distintos ritmos de reproducción
k
1
7
168
10080
604800
Tasa porcentual
5% semanal
5/7% por dı́a
5/168% por hora
5/10080% por minuto
5/604800% por segundo
P(t)
33075
33143
33154
33155
33155
Del ejercicio anterior vale la pena hacer las siguientes observaciones.
Observación. Para un ritmo de reproducción más acelerado, la población después de dos semanas
tiende a ser mayor. Por ejemplo para un ritmo diario (k = 7), la población esperada es de 33143,
mientras que para un ritmo que toma escalas de tiempo de segundos (k = 604800), la población es
de 33155 (mayor).
20
P
P
P
33 000
33 000
33 000
32 000
32 000
32 000
31 000
31 000
31 000
30 000
30 000
30 000
0.0
0.5
1.0
1.5
2.0
t
0.0
0.5
1.0
1.5
2.0
t
0.0
0.5
1.0
1.5
2.0
Figura 1.13: Gráfica de P (t) = 30000(1 + .05/k)kt , k = 1, 7, 168
Para periodos de reproducción cada vez más pequeños, la población después de dos semanas
tiene a estabilizarse en un valor determinado de aproximadamente 33155 bacterias al final de dos
semanas.
Afirmación. Si en el modelo de crecimiento exponencial a tasa porcentual constante r
r kt
,
P0 1 +
k
nos interesa predecir el comportamiento de la población a escalas de tiempo pequeñas, debemos tomar
k muy grande (esto se escribe k → ∞).
Cuando hacemos esto, la población que obtenemos se aproxima a un valor que denotamos
r kt
P (t) = lim P0 1 +
.
k→∞
k
En el ejemplo de las bacterias que acabamos de analizar se tiene
lim 30000(1 + r/k)2k ≈ 33155.
k→∞
Resulta sorprendente que esta aproximación puede calcularse mediante una fórmula, es decir, no
será necesario hacer k → ∞ para poder calcular la población tomando en cuenta escalas de tiempo
pequeñas.
Afirmación. Se tiene el lı́mite
r kt
= P0 ert .
lim P0 1 +
k→∞
k
donde e ≈ 2.71828182... es cierto número irracional (no periódico) al que se llama la base de los
logaritmos naturales.
Por tanto un modelo de crecimiento exponencial que toma en cuenta escalas muy pequeñas de tiempo,
tiene por ecuación
P (t) = P0 ert
A dicho modelo también se le denomina exponencial continuo, porque toma en cuenta que la
población crece instante a instante.
En el ejemplo de las bacterias se tiene 30000e.05 ≈ 33155
Ejemplo. Consideremos una población de peces introducidos en una presa consta de 100 mil ejemplares y crece a una tasa anual del 50 %, suponiendo un crecimiento anual, semestral, bimestral y
mensual se tiene
P (t) = 100(1 + .5/k)kt ,
con k = 1, 2, 6, 12. Sus gráficas aparecen en la fig. 1.14. Al considerar un crecimiento continuo en el
tiempo, k → ∞, de donde se tiene P (t) = 100e.5t .
21
t
PHmilesL
250
200
150
100
0.0
0.5
1.0
1.5
2.0
t
Figura 1.14: Gráficas de P (t) = 100(1 + .5/k)kt , k = 1, 2, 6, 12, y gráfica de P (t) = 100e.5t
Ejemplo. La población de México en el 2002 fue de 101.8 millones de habitantes. Si la tasa de
crecimiento era 1.4 % anual. Suponiendo que se mantiene constante.
1. Calcula la población en el 2010 utilizando el modelo exponencial continuo P (t) = P0 ekt .
2. Bajo esa misma dinámica poblacional, calcula la población que habı́a en el 2000.
Solución. Podemos considerar P0 = 101.8 millones como la población inicial, t el número de años
transcurridos desde el 2002. Para calcular la población en el 2010, utilizamos r = .014 y t =
2010 − 2002 = 8,
P (8) = 101.8e.014×8 ≈ 113.9 millones.
Gráfica de P (t) = 101.8e.014t
Para calcular la población que hubo en el 2000 hacemos t = 2000 − 2002 = −2,
P (−2) = 101.8e.014(−2) = 98.9 millones.
Ejemplo. En cierto paı́s la tasa porcentual de crecimiento es r = .04. ¿En qué proporción se habrá
incrementado la población en cinco años? Suponiendo un modelo exponencial continuo.
Solución. Como tenemos un modelo exponencial continuo se tiene P (t) = P0 ert = P0 e.04t . Después
de cinco años,
P (5) = P0 e.04(5) = P0 e.2 = P0 (1.2214)
Quiere decir que la población se habrá incrementado en una proporción
P (5)
1.2214P0
=
= 1.2214,
P0
P0
que en porcentaje se traduce en un 1.2214 × 100 = 122.14%.
22
PHmillL
150
140
130
120
110
100
90
-5
0
5
10
15
20
t
Figura 1.15: Gráfica de P (t) = 101.8e.014t
Observación. Notamos que la función exponencial P (t) = P0 ert tiene las siguientes propiedades:
A). Es creciente si r > 0
B). Es decreciente si r < 0.
C). P (0) = P0 .
D). Siempre es positiva (si P0 lo es). En particular no existe ningún valor de t para el cual
P (t) = 0.
E). Si r > 0, para valores positivos grandes de t, P (t) tiene valores grandes
F). Si r < 0, para valores negativos grandes de t, P (t) es muy cercana a 0.
1.5.2
El logaritmo natural y tiempo de duplicación
Definición. Dado una número positivo y > 0, entonces x es el logaritmo natural de y si
y = ex
y se escribe
x = ln y.
El logaritmo natural tiene la siguiente propiedad ln ex = x = eln x . La cuál es útil en algunos
problemas que involucran la función exponencial. En la fig. 1.16 aparece la gráfica de la función
logaritmo natural.
Ejemplo. Suponiendo que la población mundial crece continuamente de manera exponencial con
tasa anual 1.6 % y que en 1995 la población fue de 5770 millones de habitantes. Calcula el tiempo
para el cual la población alcanzará los 7000 millones de habitantes con este modelo. Calcula el
tiempo de duplicación de la población.
Solución. Tenemos que despejar t de la ecuación
P = P0 ert .
De la ecuación obtenemos ert =
P
P0 .
Aplicando logaritmo rt = ln PP0 , finalmente
t=
ln PP0
r
23
ln x
4
2
1
2
3
4
x
-2
-4
Figura 1.16: Gráfica de ln x
PHmillL
14 000
12 000
10 000
8000
6000
-10
0
10
20
30
40
50
t
Figura 1.17: Gráfica de P (t) = 5770e.016t
Sustituyendo r = .016, P = 7000 y P0 = 5770 obtenemos
t=
ln 7000
5770
= 12.07
.016
que corresponde al año 1995 + 12 = 2007.
Para calcular el tiempo de duplicación despejamos t de la ecuación, P = 2P0 .
Es decir, de 2P0 = P0 ert ,, obtenemos la fórmula general,
t=
ln (2)
.
r
En nuestro ejemplo particular t = ln 2/.016 = 43.32; que corresponde a aproximadamente el año
1995+43=2038.
Ejemplo. Si la población de un paı́s crece de 16 millones a 18.5 millones en 10 años. Calcula la
tasa de crecimiento en el modelo exponencial P = P0 ert . Solución. El despeje de r utilizando las
propiedades del logaritmo natural es
ln PP0
r=
t
24
yHgrL
10
8
6
4
2
[h]
0
50
100
150
200
250
300
350
tHhrsL
−.0077t
Figura 1.18: Ley de decaimiento del Rn222
86 , y(t) = 10e
Sustituyendo P = 18.5, P0 = 16 y t = 10, tenemos
r=
ln 18.5
16
= .0145.
10
que corresponde a una tasa porcentual de 1.45 % anual.
1.5.3
Decaimiento radioactivo
La función exponencial ex aparece también en otros contextos en los que se describe un decaimiento
de una cierta magnitud como función del tiempo.
Según la explicación de Rutherford para la radioactividad, los átomos de ciertos elementos muy
pesados son inestables y se transforman en otros elementos cuyos átomos son más ligeros, emitiendo;
Partı́culas α: combinación de dos protones y dos neutrones.
Partı́culas β: electrones energéticos.
Partı́culas γ: fotones de alta energı́a o rayos X.
Por ejemplo el isótopo de radón Rn222
86 es un elemento radioactivo. Rutherford descubrió que si
y0 es la cantidad original de una muestra de material radioactivo, y si y(t) es la cantidad de material
radioactivo presente en una muestra t horas después de iniciadas las observaciones, entonces
y(t) = y0 e−λt
Esta es la “ley de decaimiento radioactivo” y expresa la cantidad de material radioactivo presente
como función del tiempo. La constante λ se llama la constante de desintegración radioactiva del
elemento.
−1
Para el Rn222
.
86 , la constante radioactiva es λ = 0.0077 y sus unidades son horas
Ejemplo. Calcula la porción de material radioactivo presente en una muestra de 10 gr de Rn222
86
después de 240 horas
Solución. Tomamos y0 = 10 y entonces
y(240) = 10e−0.0077(240) = 10e−1.848 = 1.58 gramos
Consideremos la ley de decaimiento radioactivo
Q = Q0 e−λt
25
yHgrL
10
8
6
4
2
0
50
100
150
200
250
300
350
tHhrsL
Figura 1.19: Vida media de Rn222
86
donde Q0 es la cantidad original de material radioactivo, λ es la constante radioactiva, Q es la
cantidad de material radioactivo presente después de t unidades de tiempo.
La vida media, tm , de una sustancia radioactiva se define como la cantidad de tiempo requerida
para reducir a la mitad la cantidad de la sustancia radioactiva del material. Es una constante que
solamente depende de la sustancia y que se puede relacionar a la constante radiactiva, mediante la
relación
Q0
Q0
Q=
,
Q0 e−λtm =
2
2
de donde es posible obtener la relación
ln 12
ln 2
tm =
=
−λ
λ
Por ejemplo para Rn222
86 la vida media es tm = ln 2/.00779 = 88.98 horas (ver figura).
1.5.4
Fechamiento de minerales y fósiles
La función exponencial es útil en el fechamiento de minerales y fósiles para determinar el tiempo
en el que vivieron organismos o para determinar la edad de una roca. En 1960 W. Libby ganó el
Premio Nobel por su descubrimiento del método de datación de carbono. El método consiste en
considerar la proporción de carbono 14 respecto al carbono 12 presente en un tejido muerto. Debido
a que el carbono 14 decae en carbono 12, dicha proporción disminuye respecto a la proporción
carbono 14/ carbono 12 presente en la atmósfera.
Se determinó que la vida media del carbono 14 es de 5730 años por lo que su constante radioactiva
se obtiene de la relación
ln 12
ln 2
=
λ=
−tm
tm
sustituyendo tm = 5730 se obtiene λ = .00012097.
Ejemplo. Un fósil tiene 30 % del carbono 14 que contenı́a originalmente. Calcula la edad del fósil.
Solución. Basta considerar la relación QQ0 = e−λt , de donde Q/Q0 = e−λt . Empleando el
logaritmo natural a ambos lados de la ecuación
t=
ln QQ0
−λ
26
sustituyendo en nuestro caso particular se tiene
t=
1.6
ln 0.3
≈ 9953.
−.00012097
Ejercicios de repaso
1. Expresa el área de un cuadrado como función de la longitud de uno de sus lados.
2. La presión P de un gas a volumen constante es función de su temperatura de acuerdo a la
función lineal
P (T ) = kT + b
para unas constantes k y b. Supón que en un experimento cuando T = 0 o C se midió P =
760 mmHg; después cuando T = 100 o C, se midió P = 1040 mmHg.
(a) Determina el valor de las constantes k y b en este experimento. ¿Qué unidades tienen k
y b?
(b) El cero absoluto se puede aproximar haciendo P = 0. De la ecuación P = kT +b encuentra
el valor T para el que P = 0.
3. El nivel de CO2 en partes por millón (ppm) en el Observatorio Mauna Loa fue de 325.3 en
1970 y 338.5 en 1980. Asumiendo que el nivel de CO2 crece de manera lineal
(a) Encuentra la ecuación que determina la concentración de CO2 , C(x), como función lineal
del tiempo x (en años transcurridos desde 1970). ¿Cuál es la pendiente y cuál es la
ordenada al origen?
(b) Usa esta ecuación para predecir el nivel de CO2 en 1900 y en 2010.
4. La reacción del cuerpo a las drogas está dada por la ecuación
D
M
−
R(D) = D2
2
3
donde D es la dosis administrada, M es una constante que representa la dosis que produce
máxima reacción.
(a) Utiliza M = 200 y esboza la gráfica de la función utilizando los siguientes valores de D,
0, 50, . . . , 300, 350.
(b) ¿En qué intervalos es creciente/decreciente R(D)?.
5. La temperatura corporal en un individuo sigue un ciclo circadiano con un modelo dado por la
siguiente ecuación
T (t) = 0.002(t3 − 45t2 + 609t + 16000)
donde T (t) es la temperatura corporal y t es el tiempo en horas transcurrido desde las 8 hasta
el fin del dı́a, 8 ≤ t ≤ 24.
(a) Evalúa la temperatura T (t) cada 2 horas, es decir para t = 8, 10, . . . , 24.
(b) ¿En qué intervalos la temperatura es creciente/decreciente?
(c) ¿Aproximadamente a qué hora alcanza la temperatura máxima y la mı́nima?
27
6. La Ley de Enfriamiento de Newton establece que la razón de enfriamiento R de un objeto
caliente es directamente proporcional a la diferencia entre la temperatura T del objeto y la
temperatura del ambiente T0 , con constante de proporcionalidad k.
(a) Escribe la ecuación que describe R como función de T . ¿Cuál es la pendiente, la ordenada
al origen?.
(b) Suponiendo que en la cocina hay una temperatura T0 = 20o C y que cuando una tasa de
café tiene temperatura T = 40o C, entonces R = 5o C/seg, calcula la constante k.
(c) Esboza la gráfica de la recta del inciso anterior.
7. Una población de golondrinas se reproduce cada otoño (una vez al año), con una tasa de
crecimiento de r = 2% anual o r = 0.02 año, con una población inicial P0 de 10,000 ejemplares.
(a) Emplea el modelo de crecimiento con una replicación anual
P (t) = P0 (1 + r)t
donde t son los años transcurridos para calcular la población en t = 0, 1, 2, . . . , 8.
(b) Esboza la gráfica con estos valores.
(c) ¿En cuánto tiempo se duplica la población?
8. La población P de una ciudad como función del tiempo t, suponiendo el modelo utilizado en
el problema anterior, tiene la forma
P (t) = 80, 000(1.015)t
(a) Determina la razón anual de crecimiento r y la población inicial P0 .
(b) Determina el momento t en el que se duplica la población.
9. Una población crece a una tasa porcentual constante 2.5 % anual. Dentro de 5 años la población
será de 15000 individuos ¿Cuál es la población actualmente? Emplea el modelo de crecimiento
con una replicación anual P (t) = P0 (1 + r)t .
10. Una población de mosquitos se reproduce una vez al mes. Calcula la tasa de reproducción mensual si la población crece de 9000 a 9095 durante dos meses. Emplea el modelo de crecimiento
con una replicación mensual P (t) = P0 (1 + r)t
11. Una población de bacterias crece de manera continua de 6000 a 9000 células durante 24 horas.
Determina la ley de crecimiento exponencial P (t) = P0 ert .
12. Unos pergaminos datan de año 100 antes de n. e. Determina el porcentaje de carbono 14 aún
presente en la fecha de su descubrimiento en el año 1947.
13. La datación de carbono 14 del manto de Turı́n se realizó en 1988. El estudio arrojó que estaba
presente el 92.3 % del carbono 14 original del Santo Sudario.
(a) Calcula la edad probable del Santo Sudario.
(b) Calcula el porcentaje presente de carbono 14 si en realidad se tratara de una reliquia de
1960 años de edad.
(c) En el año 1398, ante el papado, el obispo Pierre d’Arcis, acusó a un colega de falsificación
del Santo Sudario. Determina si tenı́a razón el obispo en sus acusaciones.
28
14. Una población de bacterias crece de acuerdo a la ley de evolución P (t) = 1000 − 600t + 30t2 .
Donde t es el número de horas transcurridas desde iniciado el experimento.
(a) Encuentra el tiempo t0 ≥ 0, para el cuál la población se hace 0.
(b) Esboza la gráfica de la función en el intervalo [0, t0 ] .
15. Supón que la inflación en México crece de manera continua con tasa del 4.5 % anual.
(a) Si el litro de gasolina cuesta 7.9 pesos. Escribe la función que describe el precio P del
litro de gasolina en términos del tiempo t medido en años.
(b) ¿Dentro de cuántos años se duplicará el precio de la gasolina?
(c) En otro paı́s el precio de gasolina se incrementa de 7.9 a 10 pesos en 5 años ¿cuál es la
tasa de inflación en ese paı́s?
16. El rubidio 87, Rb87 , es un elemento inestable y decae exponencialmente a estroncio 87, Sr87
emitiendo radiación beta. Se le encuentra abundantemente en muchos minerales en la Tierra.
(a) Si la cantidad de Rb87 presente en un mineral se reduce a la mitad en aproximadamente
4.7 × 1010 años. Calcula la tasa λ de decrecimiento anual en el modelo exponencial
Q (t) = Q0 e−λt .
(b) En un pedazo de biotita hallado en el Gran Cañón se encontró 202 partes por millón
(ppm) de Rb87 y 3.97 ppm de Sr87 . Suponiendo que originalmente la concentración de
Rb87 en la biotita era de Q0 = 205.97 = 202 + 3.97 ppm ¿cuál es la edad de la roca?
17. Una población de pingŸinos en una reserva descendió de 2500 ejemplares en 1970 a sólo 1000
ejemplares en el 2000. Suponiendo un modelo de decrecimiento lineal calcula la población que
habrá en el 2008. Esboza la gráfica que describa el comportamiento desde 1970 hasta el 2008.
De seguir esa tendencia ¿En qué momento se extinguirá dicha especie?
18. Una población de antı́lopes migrantes del norte de Canadá está creciendo a una tasa porcentual
constante de 1.5% anual. Suponiendo un periodo de reproducción anual, si en este momento
hay 60,000 ejemplares calcula en cuánto tiempo se duplicará la población.
19. La cantidad que queda de una sustancia radioactiva después de t años está dada por Q(t) =
Q0 e−0.0001t . Si después de 5000 años hay 200 gramos de sustancia ¿Cuántos gramos habı́a
inicialmente?
20. Una cuenta de banco que capitaliza mensualmente crece de 25000 a 25060 pesos en 2 meses.
Calcula la tasa mensual de interés.
21. Al producirse x unidades de cierto artı́culo, el precio unitario de cada unidad será P (x) =
40e−.05x dólares. a) ¿Qué cantidad debe producirse para que el precio unitario sea de 10
dólares. b) Esboza la gráfica utilizando x = 0, 20, 40, 60, ..., 100.
22. En una cuenta de banco se invirtieron 45,000 pesos durante 6 meses a capitalización mensual.
Al final de estos 6 meses la cuenta ascendió a 46,200 pesos. a) Calcula la tasa porcentual
mensual de la inversión. b) Calcula a cuánto ascenderá el monto si los 45,000 se invierten
durante 25 años.
23. En una zona en recuperación del santuario de la mariposa monarca se observa 30,000 ejemplares
se incrementan a 30,560 durante un año. Suponiendo que la población de mariposas monarca
se incrementa un vez cada año a tasa porcentual constante: a) determina la tasa porcentual
de crecimiento anual, b) Calcula la población que habrá en la zona después de 10 años.
29
24. Una población de bacterias crece de acuerdo a la relación P = P0 e.05t . Encuentra t para el
cual se duplica la población.
25. Una población de bacterias crece de acuerdo a la ecuación P = 1000ert . Encuentra la razón
de crecimiento r para la cual la población llega de 1000 a los 5000 en 4 dı́as.
26. Un cultivo de E. coli crece de acuerdo al modelo exponencial, tiene un tiempo de duplicación
de 16 minutos. Cuando t = 0 se tenı́a una población P0 = P (0) = 20, 000 bacterias.
(a) Encuentra la expresión para el número de bacterias después de t horas.
(b) Encuentra el número de bacterias después de 6 horas.
(c) ¿Cuándo se tendrá una población de P = 1, 000, 000 de bacterias?
27. Un cultivo de bacterias está en fase de crecimiento exponencial. 2 horas después de iniciado
el experimento el conteo fue de 5,000 bacterias. 7 horas después habı́a 256,000 bacterias.
(a) ¿Cuál era el número de bacterias cuando inició el experimento, es decir en t = 0?
(b) Determina el número de bacterias P (t) como función exponencial para t ≥ 0.
(c) ¿Cuál es el tiempo de duplicación del cultivo?
28. Inicialmente habı́a 100 mg presentes de cierta sustancia radioactiva. Después de 6 horas
disminuyó en un 3 %. Encuentra la cantidad de sustancia radioactiva que queda después de
24 horas y determina la vida media de la sustancia.
29. En un pedazo de madera quemada de la caverna de Lascaux se encontró que un 85.5 % del
C14 ya se habı́a desintegrado. ¿Qué edad tenı́a ese pedazo de madera?
30. La planta de girasol en cierta región crece de acuerdo a la siguiente ecuación logı́stica
y(t) =
261.1
e−.613132(t−4.89)
+1
donde y es la altura promedio (en cm), t semanas después de iniciado el experimento.
(a) Esboza la gráfica de y(t) en el intervalo t ∈ [0, 12].
(b) Cuando ha transcurrido mucho tiempo ¿a qué valor se aproxima y?
30
Capı́tulo 2
La Derivada
2.1
Razón media de cambio
Definición. El cambio o variación de una función f (x) en un intervalo α ≤ x ≤ β se define como
∆f := f (β) − f (α)
La razón media de cambio o también llamada tasa media de variación de la función f (x) en
un intervalo α ≤ x ≤ β es
∆f
f (β) − f (α)
:=
∆x
β−α
Afirmación. Si f (x) es una función lineal, entonces para todo intervalo α ≤ x ≤ β, la tasa media
de cambio de f (x) en α ≤ x ≤ β es la pendiente
∆f
=m
∆x
En efecto
∆f
f (β) − f (α)
=
∆x
β−α
sustituyendo por le expresión que define la función lineal se tiene
Afirmación. Una función f (x) es creciente (respectivamente decreciente) en un intervalo (a, b)
si para todo intervalo [x0 , x1 ] contenido en (a, b), es decir, para todo a < x0 < x1 < b, se tiene que
la variación de f (x) en [x0 , x1 ] es positiva, ∆f > 0 (respectivamente negativa, ∆f < 0).
Intuitivamente la tasa media de cambio en un intervalo se interpreta como la rapidez promedio
con la que ha cambiado la función o cantidad dependiente durante el intervalo.
Ejemplo. La cantidad de larvas de mosquito presentes en un estanque t dı́as después de que se
iniciaron las observaciones, obedece la ecuación P (t) = −.5t2 + 25t + 100. Calcula la tasa media de
variación desde iniciado el experimento hasta después de a) 1 dı́a, b) 10 dı́as, c) 20 dı́as, d) 50 dı́as.
¿Cuáles son las unidades de la tasa media de variación?
Solución. Elaboramos la siguiente tabla para calcular las tasas pedidas
Intervalo
0≤t≤1
0 ≤ t ≤ 10
0 ≤ t ≤ 20
0 ≤ t ≤ 50
∆t
1
10
20
50
P (t)
124.5
300
400
100
31
∆P (t)
24.5
200
300
0
∆P (t)/∆t
24.5
20
15
0
notamos que las unidades de la tasa media de variación son las unidades de P entre las unidades
de t, es decir, en este ejemplo son larvas/dı́a. Una tasa positiva indica un crecimiento de las larvas
presentes en el estanque, en tanto que una tasa negativa indica un decrecimiento de las larvas
presentes en el estanque.
Intuitivamente, la tasa media de variación indica la rapidez promedio con la que han crecido las
larvas en el estanque durante el intervalo de tiempo indicado. Ası́ por ejemplo, una tasa media de
variación de 20 larvas/dı́a en el intervalo de 0 a 10 dı́as, se interpreta diciendo que en los primeros
diez dı́as la población de larvas creció con una rapidez promedio de 20 larvas por dı́a. Esto no quiere
decir que la población creció a un ritmo de 20 larvas por dı́a, cada dı́a, ya que por ejemplo el primer
dı́a la rapidez promedio fue de 24.5 larvas/dı́a. Más bien lo que significa es una rapidez promedio
tomando en cuenta el crecimiento neto de la población desde el inicio y hasta el final de los diez
dı́as.
Ejemplo. Supongamos que en otro estanque hay 100 larvas originalmente. Las larvas crecen a una
tasa media de variación constante de 20 larvas/dı́a cada dı́a. Encontrar la función que describe la
población de larvas en términos de los dı́as transcurridos y la tabla del ejemplo anterior.
Podemos asegurar que en la población de larvas crece de manera lineal con una fórmula P (t) =
20t + 100. En tal caso la tasa media de variación siempre vale
∆P
= 20 larvas/dı́a.
∆t
sin importar el intervalo de dı́as que se esté considerando. Ası́ por ejemplo se tendrı́a la siguiente
tabla
Intervalo
0≤t≤1
0 ≤ t ≤ 10
0 ≤ t ≤ 20
0 ≤ t ≤ 50
∆t
1
10
20
50
P (t)
120
300
500
1100
∆P (t)
20
200
400
1000
∆P (t)/∆t
20
20
20
20
EJERCICIOS
1. La cantidad de bacterias en un cultivo crece a razón media constante de 1000 bacterias por
dı́a. Si después de 4 dı́as el cultivo tiene 20,000 bacterias¿Cuántas bacterias habı́a al inicio del
experimento?.
2. Una población de bacterias que crece de acuerdo a la ley exponencial continua P (t) = 20, 000e.05t ,
donde t son los dı́as transcurridos desde iniciado el experimento. Calcula la razón media de
crecimiento en el los intervalos a) [0, 1]; b) [2, 3]; c) [3, 4]; d) [5, 4].
2.2
Razón instantánea de cambio
La tasa media de variación en un intervalo es una noción de rapidez promedio de cambio de la
función en el intervalo dado. Por tratarse de un promedio se trata de una aproximación burda que
no contiene información del comportamiento de la función dentro del intervalo.
En problemas de mecánica donde la variable independiente t es el tiempo y la variable dependiente
s(t) es la distancia, la razón media de cambio es la velocidad media del móvil. En este contexto, un
auto que recorre durante una hora un trayecto de 80 km, indica que la rapidez media promedio es
∆s
80 km
=
= 80 km/hr.
∆t
1 hr
32
que es la velocidad media en el trayecto. Esto no significa que el velocı́metro marca en todo momento
80 km/hr. La velocidad no necesariamente permaneció constante quizás disminuyó en ciertos intervalos de tiempo o quizás fue superior a 80 km/hr en otros. No obstante manteniendo un promedio de
80 km/hr. La velocidad que marca el velocı́metro en cada instante de tiempo es lo que denominamos
la velocidad instantánea del automóvil.
Mientras la velocidad media ∆s/∆t depende de un intervalo de tiempo, la velocidad instantánea
depende sólo del instante que consideremos.
Para clarificar el concepto de velocidad instantánea de un móvil analicemos el siguiente ejemplo
que concierne a la caı́da libre de un cuerpo.
Ejemplo. Supongamos que un cuerpo se deja caer desde el último piso de un edificio a una altura
de 30 m. La ecuación que describe la altura s(t) como función del tiempo t transcurrido desde que
se suelta es s(t) = 30 − gt2 /2, donde g = 9.81m/s2 . Calcula la velocidad instantánea del objeto 1
segundo después de que se soltó.
Solución. Aproximamos la velocidad instantánea como velocidades medias en intervalos de
tiempo cada vez más pequeños, digamos en los siguientes intervalos
[.9, 1], [.99, 1], [.999, 1], [.9999, 1], [.99999, 1]
Ası́ obtenemos la tabla de evaluaciones
t
.9
.99
.999
.9999
.99999
1
s(t)
26.027
25.1926
25.1048
25.0951
25.094018
25.095
que a su vez nos permite obtener ∆s en cada intervalo. Ası́ Calculamos velocidades medias
Intervalo
.9 ≤ t ≤ 1
.99 ≤ t ≤ 1
.999 ≤ t ≤ 1
.9999 ≤ t ≤ 1
.99999 ≤ t ≤ 1
∆t
.1
.01
.001
.0001
.00001
∆s
-.93195
-0.0976095
-0.0098051
-0.000980951
-0.0000980995
∆s/∆t
-9.3195
-9.76095
-9.8051
-9.80951
-9.80995
Cuando los intervalos de tiempo son cada vez más pequeños, más ”cerca” nos encontramos en
un ”instante” de tiempo. Observamos que la velocidad media se aproxima cada vez más a un valor
especı́fico −9.81 m/s, ası́ la velocidad instantánea será aproximadamente −9.81 m/s, el signo menos
significa que la altura va disminuyendo durante la caı́da.
El concepto de velocidad instantánea en problemas de mecánica, puede extrapolarse a otros
contextos y ası́ hablamos de la razón instantánea de cambio o tasa instantánea de variación
de una función f (x) en el instante x0 , como un lı́mite de la rapidez media de cambio
∆f
∆x→0 ∆x
Para el cálculo de dicho lı́mite se procede a construir aproximaciones sucesivas como en el ejemplo
que previamente analizamos.
Ejemplo. Una población de bacterias crece de acuerdo a la regla, P (t) = −5t2 + 100t + 2000.
Calcula la velocidad media en los intervalos
Razón instantánea de cambio de f en x0 = lim
[2, 2.1], [2, 2.01], [2, 2.001], [2, 2.0001]
¿Cuál es valor de la rapidez instantánea de cambio en t = 2? ¿La población crece o decrece en t = 2
33
Solución. Primero procedemos a calcular las evaluaciones de la función en los tiempos indicados,
t
2.1
2.01
2.001
2.0001
2
P (t)
2187.950000
2180.799500
2180.079995
2180.007999
2180
Enseguida calculamos rapidez media en intervalos cada vez menores de tiempo.
Intervalo
2 ≤ t ≤ 2.1
2 ≤ t ≤ 2.01
2 ≤ t ≤ 2.001
2 ≤ t ≤ 2.0001
∆t
.1
.01
.001
.0001
∆P
7.950000
.799500
.079995
.007999
∆P/∆t
79.500
79.950
79.995
79.999
Finalmente podemos decir que la rapidez instantánea de cambio en t = 2 dı́as es aproximadamente
80 bacterias/dı́a. El signo positivo indica que se trata de un crecimiento de la población.
Dada una función f (x) mediante el cálculo de la rapidez instantánea de cambio podemos definir
d
una nueva función dx
f (x) mediante la asignación
f 0 (x) =
d
f (x) := Rapidez instantánea de cambio de f en x.
dx
esta nueva función que contiene la información de la variación de f (x), se le llama la función
d
derivada. el sı́mbolo dx
es meramente formal, no tiene significado como fracción y se lee como
”derivada de...”. Al proceso de extraer la derivada de una función se le llama derivación.
d
Siguiendo la analogı́a del velocı́metro, la derivada dt
s(t) de la distancia s(t) es la función que
rige el comportamiento del velocı́metro y que en cada momento t indica la velocidad en ese instante.
Existe un método más sencillo para calcular velocidades instantáneas que no involucra realizar
aproximaciones sucesivas. En dicho método se calcula la función derivada a partir de fórmulas
generales.
EJERCICIOS
1. Una piedra se lanza verticalmente con una velocidad de 10 m/s. La altura y(t) (en metros)
como función del tiempo t (en segundos) está dada por y(t) = 10t−gt2 /2, donde g = 9.81m/s2
es la aceleración de la gravedad. Usando un intervalo de tiempo muy pequeño, calcula aproximadamente la velocidad instantánea en a) t = 0; b) t = 1 seg; c) t = 2 seg; d) ¿Qué significa
una velocidad positiva, negativa o nula?
2. En cierto paı́s el ingreso anual per capita ha tenido la siguiente evolución a lo largo del tiempo
Año
2005
2006
2007
2008
2009
2010
Ingreso per capita
5,435
5,705
5,893
6,056
6,152
6,649
Calcula las tasas medias de variación
(a) Entre 2005 y 2006.
34
(b) Entre 2005 y 2010.
(c) Entre 2006 y 2008.
3. Las temperaturas máximas en Morelia durante una semana se comportaron de la siguiente
manera
Dı́a Temperatura (C)
Domingo
20
Lunes
23
Martes
25
Miércoles
30
Jueves
33
Viernes
31
Sábado
32
Calcula las tasas medias de variación entre
(a) lunes y jueves;
(b) martes y miércoles;
(c) domingo y sábado
4. Una población de bacterias crece de acuerdo a la ley de evolución P (t) = 3000 − 600t +
30t2 . Donde t es el número de horas transcurridas desde iniciado el experimento. Mediante
aproximaciones sucesivas estima la tasa instantánea de variación para t0 = 5, 10, 15.
2.3
Derivación de funciones polinomiales
A partir de una función f (x), hemos establecido la existencia de una nueva función f 0 (x), dada por
f 0 (x) = Tasa instantánea de variación de f en x
dicha función se conoce como la derivada y también se denota por
el siguiente hecho crucial:
d
dx f (x).
Enseguida utilizaremos
Afirmación. La fórmula de la derivada f 0 (x) se puede obtener a partir de la fórmula de la función
en cuestión f (x).
Las reglas de derivación que utilizaremos son
1.
d
dx (c)
= 0.
2.
d
dx (x)
= 1.
3.
d
dx (cx)
= c.
4.
d
n
dx (x )
= nxn−1 .
5.
d
dx (cu)
d
= c dx
(u), donde c es una constante y u es una función de x.
6.
d
dx
7.
d
dx
8.
d
dx (u
u
c
=
d
dx (u)/c,
donde c es una constante y u es una función de x.
d
(un ) = nun−1 dx
(u).
+ v − w) =
d
dx (u)
+
d
dx (v)
−
d
dx (w).
35
d
dx (uv)
d
d
= u dx
(v) + v dx
(u).
10.
d
dx
c
u
=−
11.
d
dx
u
v
=
9.
d
c dx
(u)
u2 .
d
d
v dx
(u)−u dx
(v)
.
v2
donde c es un constante, u, v, w, son funciones de x. En particular para una función lineal
f (x) = b + mx se tiene
d
d
d
d
(b + mx) =
(b) +
(mx) = 0 + m (x) = m.
dx
dx
dx
dx
Como ya antes lo habı́amos señalado, la tasa de variación instantánea de una función lineal es la
pediente (constante) m.
Más generalmente, para una función polinomial f (x) = a0 + a1 x + a2 x2 + . . . + an xn se tiene
d
(a0 + a1 x + a2 x2 + . . . + an xn ) = a1 + 2a2 x + 3a3 x2 + . . . + nan xn−1 .
dx
Ejemplo. Para un objeto que se deja caer de un edificio de 30 m, la altura s(t) = 30 − gt2 /2, tiene
d
derivada dt
s(t) = −gt, es decir, la velocidad instantánea en la caı́da libre es v = −gt.
Ejemplo. Considera la población de bacterias que crece de acuerdo a la fórmula P (t) = −5t2 +
100t + 2000. a) Empleando el formulario, calcula la función derivada P 0 (t); b) Calcula la rapidez
instantánea de crecimiento de la población en t = 0, 5, 10, 15, 20 dı́as. c) ¿Qué significa el signo de
la rapidez positiva, negativo?
Solución. a) De las fórmulas de derivación se tiene
P 0 (t) =
d
d
d
d
(−5t2 + 100t + 2000) = (−5t2 ) + (100t) + (2000)
dt
dt
dt
dt
d 2
d
(t ) + 100 (t) + 0 = −5(2t) + 100(1) = −10t + 100.
dt
dt
b) Tenemos que hacer las evaluaciones indicadas, las resumimos en las siguiente tabla
P 0 (t) = −5
t
0
5
10
15
20
P 0 (t)
100
50
0
-50
-100
c) El signo positivo en la derivada indica un crecimiento en ese instante de la función estudiada.
Ası́ por ejemplo P 0 (0) = 100 células/dı́a > 0, indica que al inicio del experimento la población crece
a un ritmo de 100 bacterias por dı́a. Por el contrario una derivada negativa indica un decrecimiento
de la función, por ejemplo P 0 (20) = −100 bacterias/dı́a indica una disminución de la población de
bacterias a un ritmo de 100 por dı́a.
Resumimos la discusión en torno al signo de la derivada en la siguiente
Afirmación. Si la derivada es positiva en x, f 0 (x) > 0 (resp. negativa en x, f 0 (x) < 0), en
a < x < b, entonces la función f (x) es creciente (resp. decreciente) en dicho intervalo.
EJERCICIOS
1. Calcula la derivada de las siguientes funciones.
36
P
P¢
200
2500
100
2000
10
20
30
40
t
1500
-100
1000
-200
500
-300
-400
0
10
20
30
40
t
Figura 2.1: Gráfica de P (t) y P 0 (t)
f¢
-1.5
-1.0
f
4
0.4
2
0.2
0.5
-0.5
x
-1.5
-1.0
0.5
-0.5
-2
-0.2
-4
-0.4
x
Figura 2.2: Gráfica de una función y su derivada. El signo de f 0 determina si f es creciente o
decreciente
37
(a) f (x) = 2x + 3
(b) f (x) =
(c) f (x) =
x
2 + 4x
1.5x+4.5
2
2
(d) f (x) = x + 3x − 5
(e) f (x) =
2x2
3
4
−
3x
2
(f) f (x) = 4x − 2x2 + 4
(g) f (x) =
3x3 +x2 −4x+1
5
−1
−2
(h) f (x) = πx
+x
(i) f (x) = −3/x + 6/x3
(j) f (x) = 2xπ + x1/2 − 2x−3/4
√
(k) f (x) = x−3/2 + π x + √2x3
2. Una pipa contiene 20,000 litros de agua. Se abre la llave y el agua sale de la pipa a una razón
constante de 10 litros por segundo.
(a) Si V (t) es el volumen (en litros) contenidos en la pipa t segundos después de que se abre
la llave. Calcula V 0 (t). ¿Qué signo tiene?
(b) ¿Es V (t) una función lineal? Escribe una fórmula para V (t).
(c) ¿En cuánto tiempo se drena completamente la pipa?
3. El precio P (t) del litro de gasolina crece linealmente de $ 7.06 a $ 7.99 en 360 dı́as. Calcula la
tasa de crecimiento constante P 0 (t), donde t es el tiempo en dı́as. Calcula el tiempo que debe
transcurrir para que el litro cueste $ 8.50.
4. La concentración c(t) (en mg por cc) de cierta droga en el flujo sanguı́neo a tiempo t (en min),
está determinada por c(t) = 0.8 + 0.72t − 0.9t2 .
(a) Calcula la derivada c0 (t). Indica cuáles son sus unidades.
(b) Calcula la rapidez con la que cambia la concentración de droga medio minuto después de
administrada.
(c) Calcula la rapidez con la que cambia la concentración de droga un minuto después de
administrada.
(d) Evalúa c(t) y c0 (t) en t = 0, 0.1, 0.2, . . . , 0.9, 1.0. Esboza la gráfica de c(t) y de c0 (t).
(e) Calcula el tiempo t0 para el cual c0 (t0 ) = 0.
(f) Indica en qué intervalo dentro de 0 ≤ t ≤ 1, la concentración es creciente. En cuál es
decreciente.
5. Mediante métodos estadı́sticos se determinó la siguiente fórmula que expresa el módulo de
torsión del acero T (en kg/cm cuadrado) como función de la temperatura (en grados celsius)
T (t) = −0.0010268t2 − 1.8402t + 8290.11
(a) Calcula T 0 (t) e indica sus unidades.
(b) Calcula el módulo de torsión para la siguientes temperaturas: t = 0, 20, 40, 60, 80, 100
grados celsius.
(c) Calcula la razón instantánea de cambio del módulo de torsión para la siguientes temperaturas: t = 0, 20, 40, 60, 80, 100 grados centı́grados.
38
6. En una empresa se determinó que el costo marginal C(q) (en dólares por unidad) es función de
la producción q (en unidades). Si la fórmula que se determinó es C(q) = 44.4 − 1.44q + .0366q 2 .
Calcula la razón instantánea de cambio del costo marginal para 0, 10, 20, 30, 40 unidades de
producción.
2.4
Derivación de funciones exponenciales
Ahora empleamos las siguientes fórmulas de derivación que involucran a las funciones exponenciales
f (x) = eax ,
1.
d
x
dx (e )
2.
d
ax
dx (e )
3.
d
u
dx (e )
= ex ;
= aeax , donde a es una constante;
d
= eu dx
(u).
Ejemplo. Para una población que crece con una ley exponencial P (t) = P0 ert se tiene la derivada
P 0 (t) = rP0 ert .
notemos que se verifica P 0 (t) = rP (t), es decir, para cada tiempo t,
Tasa instantánea de crecimiento = Tasa porcentual de crecimiento × Población actual
Notemos también que si r > 0 y si la población inicial es P0 > 0, entonces P 0 (t) es siempre
positiva. Esto implica que la población siempre es creciente para todo momento t.
Ejemplo. Consideremos una muestra de plancton cuya población crece de manera exponencial de
acuerdo a la ley P (t) = 15, 000e.035t donde t es el tiempo transcurrido en dı́as. Calcula la rapidez
con la que crece la población 5 dı́as después.
Solución. Consideramos la derivada
P 0 (t) =
d
d
(15, 000e.035t ) = 15, 000 (e.035t ) = 15, 000(.035e.035t )
dt
dt
P 0.035t
al evaluarla en t = 5 tenemos P 0 (5) = 625.4 ≈ 625, quiere decir que en ese instante la población
crece a un ritmo de 625 organismos por dı́a.
Ejemplo. Si una población crece exponencialmente a razón porcentual constante de 2.5 %, y si al
iniciar las observaciones se observa una tasa de crecimiento instantánea de 4,500 células por hora.
Calcula la población de células con la que se inició el experimento.
Solución. Tenemos como datos r = .025 y P 0 (0) = 4, 500 en la ecuación P 0 (t) = rP (t) basta
evaluar en t = 0 y despejar P (0),
rP (t) = P 0 (t) implica P (0) = P 0 (0)/r =
4, 500
= 112.5 ≈ 112
.025
.
Ejemplo. La población de EU en un modelo exponencial creció de 1860 a 1900 de acuerdo a la
fórmula P (t) = 49.5e.022t en millones de habitantes, donde t son los años transcurridos desde 1860.
Calcula el tiempo en el cual la población crecı́a a un ritmo de 2 millón de habitantes anual.
39
Solución. Al calcular la derivada tenemos P 0.022t = 1.089e.022t . Ahora debemos encontrar t tal
que P 0 (t) = 2 es decir
2 = 1.089e.022t
Para despejar t, tenemos
2
= e.022t ≈ 1.836473
1.089
extraemos logaritmo natural y se tiene
ln e.022t = .022t = ln 1.836473
de donde finalmente t = ln 1.836473/.022 ≈ 27.6. Quiere decir que en el año de 1860 + 27.6 = 1887.6,
la población crecı́a con una rapidez instantánea de 2 millones de habitantes por año.
EJERCICIOS
1. Deriva las siguientes funciones
(a) f (x) = e3x + 3xe
(b) f (x) = 5e−2.5x
(c) f (x) = 3/eπx + e−2x
2. Utiliza la regla de derivación
d u
d
(e ) = eu (u), donde u es una función de x
dx
dx
d n
d
(u ) = nun−1 (u)
dx
dx
para calcular la derivada de la funciónes siguientes
(a) f (x) = e3x+2
(b) f (x) = πe−3x
(c) f (x) =
2
+3x−1
π
e−3x2 +3x−1
(d) f (x) = e−(x−2)
2
(e) f (x) = 2x + π x + ln 2. Sugerencia: 2 = eln 2 .
(f) f (x) = ln e−3x
(g) f (x) = eln(
√
1/2
x−x
+x
−1/2
)
3. Considera la función
f (x) = e− 2 (
1
x−µ
σ
2
) , donde µ, σ > 0 son constantes
(a) Usando µ = 1, σ = 3, verifica que f (x) tiene un máximo en x = µ = 1.
(b) Calcula la segunda derivada f 00 (x).
(c) Verifica que la derivada f 0 (x) tiene un máximo en x = µ − σ y un mı́nimo en x = µ + σ.
(d) esboza las gráficas de f (x) y f 0 (x) usando x = −4, −3, . . . , 6.
4. La cantidad de contaminantes Q (en km3 ) presente en un lago t años después de que se vierten
desechos en él, decae de manera exponencial, de acuerdo a la fórmula
Q(t) = Q0 e−rt
donde Q0 es la cantidad original de deshechos vertidos y r es una constante de degradación.
40
(a) Si 5 años después de vertidos 2 km3 de deshechos en un lago, estos se degradan a 1.5
km3 . Calcula la constante r.
(b) Calcula la razón instantánea de decrecimiento 10 años después de vertidos 2 km3 de
deshechos en un lago.
(c) Calcula cuánto tiempo tomará remover 90 % de la contaminación del lago. Es decir,
después de cuánto tiempo permanecerán 10 % de los desechos aún sin degradar.
(d) Calcula después de cuánto tiempo se habrá removido el 99 % de la contaminación.
(e) Determina que pasa con la contaminación para t muy grande.
5. El número N de personas que han escuchado un rumor difundido por los medios masivos de
comunicación es una función del tiempo dada por
N (t) = a(1 − e−kt )
donde a es la cantidad de personas en la población en cuestión, y k es la tasa porcentual de
personas que escuchan el rumor en un dı́a. Si a = 200, 000 y k = .1 es decir 10%. Encuentra
la rapidez con la que se propaga el rumor 1, 2 y 3 dı́as después de que se inició.
6. La temperatura de un pastel que se saca a enfriar de un horno a 200 grados centı́grados, es
una función del tiempo (medido en minutos) dada por
T (t) = (TA − TH )(1 − e−kt ) + TH
donde TA = 20 es la temperatura ambiente a la que inicialmente se colocó el pastel, TH = 200
es la temperatura del horno.
(a) Si después de 10 minutos el pastel está a 40 grado, calcula la constante k.
(b) Encuentra la rapidez (en grados/minuto) con la que decrece la temperatura, cuando recién
se saca del horno.
(c) Describe que pasa con la temperatura del pastel para t muy grande.
7. La reacción R a cierta dosis D de un medicamento, se modela mediante la función
R(D) = 10De−0.02D
(a) Calcula la derivada R0 (D).
(b) Resuelve la ecuación R0 (D) = 0.
(c) Esboza la gráfica de R(D) usando D = 0, 10, . . . , 100. Calcula para que dosis se tiene la
reacción máxima y cuál es esa reacción.
2.5
Problemas de máximos y mı́nimos
Hemos discutido como el signo de la derivada indica la tendencia creciente o decreciente de la función
en un punto. Los puntos donde la derivada es 0 también arrojan información importante acerca de
la tendencia de la función. Ası́ se tiene la siguiente
Afirmación. Supongamos que la derivada de una función f (x) se anula en x0 , f 0 (x0 ) = 0, decimos
que x0 es un punto crı́tico.
Si en un intervalo a < x0 < b, se tiene f 0 (x) > 0 para a < x < x0 y f 0 (x) < 0 para x0 < x < b.
Entonces f (x0 ) > f (x) para todo a < x < b, x 6= x0 . Al valor que toma la función en dicho punto
x0 se le llama un máximo local o máximo relativo.
Si en un intervalo a < x0 < b, se tiene f 0 (x) < 0 para a < x < x0 y f 0 (x) > 0 para x0 < x < b.
Entonces f (x0 ) < f (x) para todo a < x < b, x 6= x0 . Al valor que toma la función en dicho punto
x0 se le llama un mı́nimo local o mı́nimo relativo.
41
c
c¢
1.5
0.5
0.5
1.0
1.5
2.0
2.5
3.0
x 1.0
-0.5
0.5
-1.0
-1.5
0.5
1.0
1.5
2.0
2.5
3.0
t
Figura 2.3: Determinación de un máximo local para c(t) = 1.2 + .8t − 0.4t2
Ya habı́amos encontrado algunos problemas en donde era relevante conocer los máximos y
mı́nimos locales de una función, en tales circunstancias nos limitábamos a utilizar métodos gráficos
para tener una idea aproximada de donde se encontraba el máximo o mı́nimo local en cuestión.
Ahora, la derivada proporciona una herramienta útil para resolver el problema de encontrar máximos
y mı́nimos locales. El método que emplea la derivada tiene la ventaja de que es un procedimiento
analı́tico y plenamente justificado, a diferencia del método gráfico que solamente proporciona una
”idea” y una aproximación.
Ejemplo. Supongamos que la concentración c(t) de un medicamento, t minutos después de ser
administrado en la sangre, obedece la fórmula c(t) = 1.2 + .8t − 0.4t2 . a) Calcula el momento en el
que la concentración alcanza el máximo; b) Cuál es la máxima concentración.
Solución. a) Calculamos la derivada y obtenemos
c0 (t) = 0.8 − 0.8t
Para calcular un máximo o mı́nimo local primero calculamos los t0 tales que c0 (t0 ) = 0. En nuestro
caso 0.8 − 0.8t = implica t = 1. Para verificar que se trata de un máximo basta ver que si 0 < t < 1
entonces c0 (t) = 0.8 − 0.8t > 0; en tanto que si 1 < t entonces c0 (t) < 0.
b) La concentración máxima será c(1) = 1.2 + 0.8(1) − 0.4(1)2 = 1.6.
Ejemplo. Supón que la altura que alcanza un objeto arrojado hacia arriba con una velocidad inicial
v0 > 0 (en m/s) obedece la ley
1
s(t) = − gt2 + v0 t,
2
donde g = 9.81 es la aceleración de la gravedad. Muestra que alcanza una altura máxima en t = v0 /g,
y que dicha altura es smax = v02 /2g.
Solución. Al calcular la derivada tenemos la velocidad vertical
d
1 2
0
v = s (t) =
− gt + v0 t = −gt + v0
dt
2
haciendo v = 0 se tiene −gt0 + v0 = 0 de donde t0 = v0 /g, al sustituir se tiene
1
smax = s(t0 ) = − g
2
v0
g
EJERCICIOS
42
2
+ v0
v0
g
=
v02
.
2g
1. En un lago la población de peces es P , H es un parámetro conocido como la razón de pesca,
es decir la cantidad de peces que se extraen por unidad de tiempo (peces/año). La tasa de
crecimiento de la población de peces como función de la población está dada por
R(P ) = 2P − 0.02P 2 − H
Para cada uno de los siguientes valores del parámetro H = 75, 100, 200 esboza la gráfica de
R(P ) contra P . Encuentra el valor de P para el cuál la tasa de crecimiento es máxima.
2. En un dı́a se ha encontrado que la velocidad del tráfico en una avenida principal es v(t) =
t3 − 10.5t2 + 30t + 20 millas por hora, donde t son las horas después del mediodı́a. Esboza la
gráfica usando t = 1, 2, 3 . . . 6. Calcula el momento en el tráfico es más rápido y en el que es
más lento. Calcula las velocidades máximas y mı́nimas.
3. La temperatura corporal en un individuo sigue un ciclo circadiano con un modelo dado por la
siguiente relación
T (t) = 0.002(t3 − 45t2 + 609t + 16000)
donde T (t) es la temperatura corporal y t es el tiempo en horas transcurrido desde las 8 hasta
el fin del dı́a, 8 ≤ t ≤ 24. Encuentra la temperatura máxima y mı́nima y a qué hora del dı́a se
alcanza.
4. Una encuesta indica que x meses después de que se lanza una candidatura a presidente. Cierto
1
(−x3 + 6x2 +
candidato obtiene S(x) por ciento de la intención de voto, donde S(x) = 29
63x + 1080), esboza la gráfica utilizando x = 0, 1, 2, . . . , 12. A) ¿Después de cuántos meses, la
candidatura tiene la mayor intención de voto? ¿de cuánto es ese porcentaje?
2.6
Ejercicios de repaso
1. La reacción del cuerpo a las drogas está dada por la ecuación
D
M
−
R(D) = D2
2
3
donde D es la dosis administrada, M es una constante que representa la dosis que produce
máxima reacción.
(a) Utiliza M = 200 y calcula la derivada R0 (D) = dR/dD.
(b) Evalúa la derivada en los siguientes valores de D
0, 50, 100, 150, 200, 250, 300, 350
esboza la gráfica de R0 (D). Compara con el ejercicio del capı́tulo anterior.
2. La gráfica 2.4, muestra el crecimiento de la estatura E(x) de un individuo como función de su
edad x. E se mide en cm y x en años. Se hicieron mediciones cada cumpleaños, obteniéndose
los datos:
45, 59, 64, 74, 90, 108, 115, 118, 122, 131, 132, 135, 140, 154, 172, 179, 184, 186, 188, 189.5, 190.
(a) Determina el cambio ∆E y la razón media de cambio ∆E/∆x en los intervalos
[13, 18], [13, 17], [13, 16], [13, 15], [13, 14].
43
Estatura
150
100
50
0
5
10
15
20
Edad
Figura 2.4: Estatura como función de la edad
(b) Usa las aproximaciones sucesivas del inciso anterior para dar el valor aproximado de la
tasa o rapidez instantánea de crecimiento a los 13 años, E 0 (13).
(c) Emplea el mismo procedimiento para calcular un valor aproximado de la tasa instantánea
de cambio a los 17 años, E 0 (17).
(d) ¿A qué edad se produce el ”estirón”, es decir el crecimiento más rápido de la estatura?
3. Una población de chimpancés en cierto habitat tiene el siguiente modelo de crecimiento
P (t) = 100(1 + 0.3t + 0.04t2 )
donde P (t) es la población, t es el tiempo transcurrido en meses.
(a) Calcula la razón de crecimiento P 0 (t).
(b) Esboza la gráfica de P 0 (t) utilizando t = 0, 10, 20, . . . , 100.
4. La razón de crecimiento anual r de una población de rapaces está dada por la relación
r(P ) = 0.02P − 0.000025P 2
donde P es la población de ese año.
(a) Esboza la gráfica para P = 100, 200, . . . , 1000.
(b) La población está en equilibrio cuando la razón de cambio r es 0. Determina las poblaciones P para las que estas aves se encuentran en equilibrio.
(c) Encuentra la derivada de la razón de cambio r0 (P ) = dr/dP .
(d) Resuelve la ecuación r0 (P ) = 0 para encontrar la población P para la que la razón de
cambio r es máxima.
5. El gasto total de energı́a por dı́a en crı́as (cervatillos) de antı́lopes americanos se estimó utilizando la ”fórmula de Nagy”
E(x) = 0.774 + 0.727 ln x
donde x es el peso (en gr ) de la crı́a, y E(x) es el gasto de energı́a (en kJ/dı́a).
(a) Esboza la gráfica para x ∈ [5000, 20000].
44
(b) Calcula E 0 (x). ¿Cuáles son sus unidades?.
(c) Calcula E(10000) y E 0 (10000). Da una interpretación biológica de estas cantidades.
6. Supongamos que en un tratamiento la concentración h(t), de cierta hormona es función del
tiempo transcurrido t:
h(t) = 40(e−0.005t − e−0.15t )
donde h se mide en nanogramos por decilitro de sangre (ng/dl ) y t en dı́as.
(a) Calcula h0 (t).
(b) Encuentra t para el cual se tiene la mayor concentración de la hormona en la sangre.
7. De 1750 a 1880 se tiene un modelo exponencial de crecimiento poblacional mundial
P (t) = 760e.005t
donde P (t) es la población mundial t años después de 1750. De acuerdo a este modelo ¿cuál
era la tasa de crecimiento de la población en 1800?
8. En un estudio psicológico se quiere conocer como se olvida la información visual conforme
transcurre el tiempo. Para estudiar el porcentaje de retención R de ciertas palabras después
de transcurridos t horas. Se obtuvo la relación
R(t) = 30 + 70e−.46t
(a) ¿Cuánto tiempo después se ha olvidado el 50% de la información?
(b) Esboza la gráfica para 0 ≤ t ≤ 12.
(c) ¿Aproximadamente qué porcentaje de la información ya no se olvida después de transcurrido mucho tiempo? en otras palabras ¿Cuánto vale R(t) si t es muy grande digamos
t = 100, 1000?
(d) Calcula R0 (t). ¿Cuánto vale R0 (t) para valores muy grandes de t?
9. Un estudio de eficiencia en el trabajo muestra que un trabajador promedio que llega a las 8:00
hrs habrá producido Q(t) = −t3 + 8t2 + 15t unidades t horas después. Calcula la tasa de
producción Q0 (t) del trabajador. Calcula la tasa de producción a las 9:00 hrs.
10. Indica si las siguientes funciones son crecientes, decrecientes en toda la recta numérica a)
−3.2 + 2.5x; b) 3.2e−3t ; c) 0.5e2.3t
11. Un ornitólogo determina que aproximadamente en un periodo de 17 horas, la temperatura
corporal de cierta especie de aves fluctúa de acuerdo con la fórmula T (t) = −68.7t3 + 30.98t2 +
12.52t + 37.1 para 0 ≤ t ≤ 0.713 donde T es la temperatura medida en grados celsius t dı́as
después del inicio de un periodo.
(a) Calcula e interpreta la derivada T 0 (t).
(b) Calcula la razón a la que cambia la temperatura al inicio del periodo (t = 0) ¿Aumenta
o disminuye la temperatura?
(c) ¿En qué instante no cambia la temperatura, no aumenta ni disminuye?. Calcula la temperatura en ese instante.
12. Se estima que después de t meses un empleado postal promedio puede clasificar Q(t) = 700 −
400e−0.5t cartas por hora.
45
(a) ¿Cuántas cartas por hora puede clasificar un empleado nuevo?
(b) Calcula la rapidez de aprendizaje Q0 (t)
(c) Calcula la rapidez de aprendizaje en t = 0, 2, 4, 6, 8.
13. El yodo radioactivo tiene una vida media de 20.9 horas. a) Utilizando la ley de decaimiento
radioactivo Q(t) = Q0 e−λt
(a) calcula cuánto yodo radioactivo permanece en el resto del cuerpo del paciente (fuera de
la tiroides) 25 horas después de la inyección.
(b) Calcula la rapidez con la que el yodo se está desintegrando 25 horas después de la inyección.
14. En su fase inicial, de 1984 a 1990, el SIDA crecı́a de acuerdo a la función cúbica C(t) =
−170.36t3 + 1707.5t2 + 1998.4t + 4404.8, donde C es el número reportado de casos, y t es el
número de años transcurridos desde 1984, 0 ≤ t ≤ 6.
(a) Calcula e interpreta la derivada C 0 (t).
(b) Calcula la tasa de propagación de la epidemia en 1984.
(c) Calcula el número de casos reportados en 1990.
(d) Calcula en qué momento el número de casos fue máximo de acuerdo a este modelo y cuál
fue el número máximo de casos.
(e) Calcula en qué momento se propagó la enfermedad con mayor rapidez.
15. En una proyección de 5 años, la población P de cierta comunidad crece después de t años de
acuerdo a la fórmula P (t) = −t3 + 9t2 + 48t + 200.
(a) Calcula la razón de crecimiento de la población dentro de 3 años.
(b) ¿Crece o decrece la población dentro de 3 años?
(c) Calcula la tasa de cambio dentro de 5 años.
16. Se ha estimado que el costo mensual de producción de x unidades de un artı́culo es C(x) =
0.06x + 3x1/2 + 20 cientos de dólares.
(a) Calcula el costo de producción de 2500 unidades,
(b) Calcula la tasa de cambio del costo por unidad producida cuando la producción alcanza
las 3000 unidades.
17. Una niña cae en un lago a una temperatura de -3 grados centı́grados. Su temperatura corporal
después de t minutos en el agua es T (t) = 35e−0.32t . Ella perderá la conciencia cuando su
temperatura corporal llegue a 27 grados.
(a) ¿Cuánto tiempo tiene los socorristas para salvarla?
(b) ¿Qué tan rápido desciende la temperatura corporal cuando acaba de caer al agua?
18. Se estima que si se gastan x miles de dólares en publicidad, se venderán Q(x) = 50 − 40e−0.1t
miles de dólares de un artı́culo.
(a) ¿Cuánto se venderá si no se gasta en publicidad?
(b) ¿Cuánto se venderá si se gastan 8 mil dólares en publicidad,
46
(c) Calcula la tasa de cambio de las ventas por mil dólares de publicidad cuando ya se han
gastado 8 mill dólares de publicidad.
19. Una población P de una colonia de bacterias t dı́as después del inicio de la observación se
modela mediante la función cúbica P (t) = 1.035t3 + 103.5t2 + 6900t + 230000.
(a) Calcula e interpreta la derivada.
(b) Calcula la tasa de cambio de la población después de un dı́a, ¿crece o decrece la población?
(c) Calcula la población inicial.
(d) Calcula la razón de cambio de la población después de 10 dı́as.
(e) Calcula la población máxima en el intervalo 0 ≤ t ≤ 20.
20. Se ha obtenido que si se publicita un producto por televisión, el número N de personas (en
millones) enteradas del producto t dı́as después de que se inicia la transmisión de los comerciales
correspondientes es N (t) = 2 − 2e−.037t .
(a) Calcula el número de personas enteradas, 2 dı́as después,
(b) Calcula la rapidez con la que las personas se están enterando del nuevo producto al inicio
de la campaña;
(c) Calcula el momento en el que se han enterado 1.5 millones de personas de la publicidad.
21. Un médico inyecta 5 mg de tinte en una vena cerca del corazón y determina que la concentración
del tinte después de t horas es C(t) = −0.027t2 + 0.672t mg/L.
(a) Calcula C 0 (t),
(b) Esboza la gráfica de C(t) y de C 0 (t) usando t = 0, 4, 8, . . . , 24.
(c) Calcula el momento que la concentración es máxima.
(d) Calcula la concentración máxima.
22. Los registros indican que x años después del 2000, el impuesto predial para una casa de cuatro
recámaras, fue de I(x) = 3x2 + 40x + 1800.
(a) ¿Cuál fue el impuesto en el 2005?
(b) ¿Cuál fue la tasa de crecimiento del impuesto en el 2003?
23. El costo de producir x miles de unidades de cierto bien es C(x) = 9x + 5e−20x
(a) Calcula C 0 (x);
(b) Esboza la gráfica de C(x), C 0 (x), en x = 0, 0.1, 0.2, 0.3, 0.4, 0.5.
(c) Determina el número de unidades que hacen que el costo sea mı́nimo.
(d) Calcula el costo mı́nimo.
24. En un modelo el número de palabras N (t) que un niño aprende t semanas después de que
aprende a hablar está dada por la relación
N (t) = 71.4 ln(0.3t + 1))
(a) Esboza la gráfica en el intervalo [1, 24].
47
250
200
150
50
100
150
200
Figura 2.5: Aumento de la actividad gamma en el cerebro, detectado en electroencefalograma
(b) Calcula el número de palabras que conocerı́a 18 meses después. ¿En cuánto tiempo se
habrá duplicado ese número de palabras?
(c) Utiliza que
d
1 d
ln u =
u
dx
u dx
y Calcula la derivada N 0 (t) = dN/dt.
(d) ¿Con qué velocidad está el niño aprendiendo seis meses después de que empezó a hablar?
25. La gráfica 2.5 corresponde a mediciones hechas con un encefalograma para determinar el potencial de la actividad gamma en el cerebro durante el periodo meditativo. El eje x corresponde
al tiempo transcurrido (medido en segundos) y el eje y al potencial eléctrico V (en µVolt2 ).
Determina el cambio ∆V y la razón media de cambio ∆V /∆x, de la actividad gamma en los
intervalos [0, 50], [50, 100], [100, 150].
48
Capı́tulo 3
La Integral
3.1
Integral Definida: Areas bajo la gráfica
Supongamos que la producción de granos de cierto paı́s se describe de acuerdo a la siguiente tabla
x (años)
f(x) (miles tons.)
1
105
2
167
3
81
4
115
5
227
6
235
7
240
8
244
Es claro que si nos pidieran calcular cuál fue la producción total de granos producidos durante
estos 8 años, tendrı́amos que hacer una suma
8
X
f (x) = 105 + 167 + 81 + 115 + 227 + 235 + 240 + 244 = 1414
x=1
Si representamos la producción f (x) como una función escalonada, tendremos que la suma anterior corresponde al área debajo de la gráfica de f (x).
mil tons
250
200
150
100
50
0
2
4
6
8
años
Figura 3.1: El área bajo la gráfica de una función escalonada representa la producción acumulada
Sin embargo una función rara vez tiene una forma escalonada.
Por ejemplo, supongamos que una pequeña represa que originalmente contiene 100, 000 lt de
agua. Supongamos que x representa el tiempo (en seg) después de que se abre la compuerta y que
el agua sale a razón de 350 lt/seg. Entonces, si nos preguntamos cuál es el volumen de agua que ha
salido después de x segundos, tendremos que dicho volumen es 350x. Por ejemplo, después de 10
49
seg. habrán salido 350(10) = 3500 litros de la presa. Además es posible interpretar dicha cantidad
como el área de un rectángulo en el plano cartesiano, con base en el intervalo [0, 10] del eje x, y
altura 350. En ese sentido es el área de la región del plano comprendida entre el eje x y la gráfica
de la función constante f (x) = 350, y entre las rectas x = 0 y x = 10.
flujo
350
300
250
200
150
100
50
-2
2
4
6
8
10
tiempo
Figura 3.2: El volumen de agua que sale está representado por el área rectangular debajo de la
gráfica de f (x) = 350.
Con estos ejemplos queremos ilustrar la utilidad del cálculo de áreas debajo de gráficas. Sin
embargo, dicho cálculo puede no ser tan sencillo como en el ejemplo siguiente.
Ejemplo. La gráfica fig. 3.3, corresponde a la velocidad de un vehı́culo que se desplaza a velocidad
variable. Para calcular el trayecto requerimos obtener el área bajo la gráfica. Empleando las fórmulas
conocidas para el área de triángulos y rectángulos se obtiene la distancia recorrida.
v-
km
hr
100
80
60
40
20
1
2
3
4
5
t - hr
Figura 3.3: El área bajo la gráfica de la velocidad como función del tiempo es la distancia recorrida
Ejemplo. Supongamos que x horas después de iniciado un experimento, una población de bacterias
crece con una rapidez (no constante) de 3000x células por hora después de transcurridas x horas.
Esto significa por ejemplo que después de 1 hr. crece a velocidad de 3000(1) = 3000 células/hr.,
después de 1.5 horas crece a razón de 3000(1.5) = 4500 células/hr. Y ahora nos preguntamos, cuál
es la población de bacterias que se ha agregado después de transcurridas x = 5 horas.
Representamos la tasa (instantánea) de crecimiento como una función f (x) = 3000x, de las x
horas transcurridas. Si calculamos la tasa de crecimiento al inicio de cada hora tendremos
x (horas)
f(x) (bacterias/hora)
1
3000
2
6000
3
9000
4
12000
5
15000
Si suponemos que la razón de crecimiento se mantiene constante cada hora, se tiene una tasa de
crecimiento durante la primera hora (3000 bacterias/hora), otra tasa durante la segunda hora (6,000
50
bacterias/hora), y ası́ sucesivamente. Entonces el cálculo de las bacterias que se incorporaron a la
población se hace mediante la suma
5
X
f (x) = 3000 + 6000 + 9000 + 12000 + 15000 = 45000 bacterias
k=1
Sabemos, sin embargo que f (x) no se mantiene constante entre dos horas sucesivas. Ası́ por
ejemplo evaluando la tasa de crecimiento cada media hora tenemos
x (horas)
0.5
1
1.5
2
2.5
3
3.5
4
4.5
5
f(x) (bacterias/hora)
1500
3000
4500
6000
7500
9000
10500
12000
13500
15000
Ası́ por ejemplo, si suponemos que la tasa de crecimiento se mantiene constante cada media hora,
entonces concluimos que durante la primera media hora se agregan
bacterias
1500
× (0.5 hora) = 750 bacterias.
hora
Y haciendo la suma correspondiente se recuenta un total de
1500(0.5) + 3000(0.5) + . . . + 15000(0.5) =
10
X
f (k · (0.5)) × (0.5) = 41, 250 bacterias
k=1
Hemos obtenido dos resultados diferentes 45000 y 41250 sin embargo podemos afirmar que el segundo procedimiento es más preciso porque hemos supuesto que f (x) se mantiene constante (aunque
sabemos que no lo es) en intervalos de tiempo más cortos. Por otro lado el cálculo del área debajo
de la gráfica de f (x) = 3000x desde x = 0 hasta x = 5. Siendo su gráfica un triángulo, dicha área
se calcula como
5 × (3000 · (5))
base × altura
=
= 37, 500
2
2
Esta área corresponde a la cantidad buscada, es decir, el número de bacterias que se agregan a
la población inicial después de 5 horas.
La justificación geométrica de este hecho es que el área del triángulo que corresponde al área
bajo la gráfica, se puede aproximar cada vez mejor mediante sumas de áreas de rectángulos tomando
bases cada vez más pequeñas.
Definición. El área bajo la gráfica o integral definida de una función f (x) en un intervalo
α ≤ x ≤ β, es el área de la región del plano comprendida entre el eje x, la gráfica de f (x), y las
rectas x = α y x = β. El área tiene signo, es positiva si la gráfica está contenida en el semiplano
superior del eje x, y es negativa si la gráfica de f (x) está contenida en el semiplano inferior del eje
x. Dicha área se denotará simbólicamente como
Z β
f (x)dx
α
51
celulas
celulas
celulas
15 000
15 000
15 000
10 000
10 000
10 000
5000
5000
5000
0
1
2
3
4
5
horas
0
1
2
3
4
5
horas
0
1
2
3
4
5
horas
Figura 3.4: Aproximación del área triangular mediante sumas de áreas de rectángulos
Rβ
La notación α f (x)dx sugiere un proceso de aproximaciones sucesivas mediante sumas de áreas
de N rectángulos
N
X
f (xk )(xk − xk−1 )
k=1
donde las bases de los rectángulos son xk − xk−1 y las alturas son f (xk ). Los puntos α = x0 < x1 <
x2 < . . . < xN = β forman una colección de puntos del intervalo [α, β], también llamada partición
de [α, β].
En el ejemplo anterior hemos aprendido que por ejemplo el área bajo la gráfica de la función
f (x) = 3000x en el intervalo [0, β] se puede calcular como el área de un triángulo con base β > 0 y
altura 3000β. Es decir,
Z
β
3000xdx =
0
β(3000β)
= 1500β 2
2
R5
en particular para β = 5, 0 3000xdx = 1500(25) = 37500 representa las células que se han agregado
después de 5 horas.
Rβ
Para una función lineal de la forma f (x) = mx, se puede verificar que 0 = mβ 2 /2 (¿porqué?).
Y con un poco más de trabajo es posible justificar geométricamente la siguiente
Afirmación. Para una función lineal f (x) = mx + b, el área bajo la gráfica o integral definida en
un intervalo [α, β] es
Z β
α2
β2
+ bβ − m
+ bα .
(mx + b) dx = m
2
2
α
Ejemplo. Supongamos que la cantidad de agua que en una lluvia un rı́o lleva agua a una velocidad
creciente de v(x) = 20x + 300 litros cada segundo. Suponiendo que inunda un valle, calcula la
cantidad de agua vertida en el valle durante 50 segundos.
La cantidad de agua vertida durante 50 segundos es
Z 50
20x + 300dx = 10x2 + 300x |50
0
0
= 10(50)2 + 300(50) − [10(0)2 + 300(0)] = 40000
EJERCICIOS
1. Calcula el área bajo la gráfica
R3
−2
1.5x + 4dx.
2. La tasa de crecimiento de la biomasa en un lago es f (x) = 2.5x + 2 toneladas por dı́a, donde
x son los dı́as transcurridos. Calcula la biomasa acumulada en el lago desde inicio del dı́a 3
hasta el final de dı́a 10.
52
litros
seg
2000
1500
1000
500
-20
0
20
40
Figura 3.5: Cálculo del área bajo la gráfica
60
R 50
0
seg
20x + 300dx
3. Un rı́o lleva un caudal constante de 20 litros por segundo. Una presa capta todo ese caudal.
Calcula el agua acumulada en la presa durante 10 dı́as. Suponiendo que el rı́o experimenta
un crecimiento lineal del caudal en época de lluvias dado por v(x) = 20 + .0005x, donde x
son los dı́as transcurridos desde el inicio de la época de lluvias. Calcula la cantidad de agua
acumulada en la presa durante los primeros 10 dı́as de la época de lluvias.
4. Una colonia de bacterias originalmente es de 20000 bacterias y crece con una rapidez de 50x
bacterias cada hora, donde x son las horas transcurridas desde el inicio de las observaciones.
Calcula la cantidad acumulada de células durante una hora.
5. Un aljibe se llena con una llave abierta durante 3 dı́as. La llave lleva 1 litro cada minuto
durante el primer dı́a, 2 litros/minuto el segundo dı́a y 0.5 litros/minuto durante el tercer dı́a.
Calcula la cantidad total de agua almacenada por el aljibe.
3.2
Integral Indefinida: Antiderivada
Para las funciones no lineales (por ejemplo f (x) = 3x2 + x − 1) los argumentos geométricos son
Rβ
obsoletos para calcular la integral definida α f (x)dx. El Teorema Fundamental del Cálculo permite
traducir el problema de cálculo de áreas bajo gráficas en un problema inverso de cálculo de derivadas
es decir antiderivadas.
Afirmación (Teorema Fundamental del Cálculo 1). Sea F (x) una función tal que F 0 (x) = f (x),
entonces el área bajo la gráfica de f (x) en el intervalo [α, β], se puede calcular como
Z β
f (x)dx = F (β) − F (α).
α
Definición. Una función F (x) se llama antiderivada, primitiva o integral indefinida de f (x),
si F 0 (x) = f (x).
De esta manera hay una correspondencia entre el problema de calcular áreas bajo la gráfica y el
cálculo de antiderivadas.
La antiderivada de una función f (x), no es única. Por ejemplo F (x) = x2 es antiderivada de
f (x) = 2x; pero también G(x) = x2 + 1 es antiderivada, G0 (x) = F 0 (x) = f (x). La ambigüedad al
definir la antiderivada es una constante.
53
Afirmación. Si F (x) y G(x) son antiderivadas de f (x) (una función continua) entonces F (x) =
G(x) + C, donde C es una constante.
Ası́ la forma más general de la antiderivada de 2x es x2 + C donde C es una constante llamada
constante de integración. Cuando no se especifica la constante de integración la expresión x2 + C se
llama integral indefinida de 2x y se denota
Z
2xdx = x2 + C
R
En general, la integral indefinida de una función f (x) se denota
f (x)dx y es otra función definida
R
salvo una constante. A la función f (x) en la expresión f (x)dx se le llama integrando de la
integral indefinida.
En una segunda parte del Teorema Fundamental del Cálculo se puede verificar que la derivada
de la integral indefinida de una función es la función original.
Afirmación (Teorema Fundamental del Cálculo 2). Sea f (x) una función (continua) en un intervalo
[α, β] , entonces la función F (x) definida como
Z
x
F (x) :=
f (x)dx
α
(es derivable y) satisface F 0 (x) = f (x).
Notemos que el Teorema Fundamental del Cálculo 2 permite concluir que
Z
d
f (x)dx = f (x)
dx
Las siguientes reglas básicas de integración se deducen de las fórmulas de derivación que expusimos en el capı́tulo de la derivada
Integrales Básicas
1.
R
dx = x + C
2.
R
R
R
f (x) + g(x)dx = f (x)dx + g(x)dx
R
R
3. cf (x)dx = c f (x)dx
4.
R
xn dx =
5.
R
an xn + an−1 xn−1 + . . . + a1 x + a0 dx = an xn+1 + an−1 xn + . . . + a1 x2 + a0 x + C, n 6= −1
6.
R
ex dx = ex + C
xn+1
n+1
+ C, n 6= −1
n+1
n
2
eax dx = a1 eax + C
R
R
8. x1 dx = x−1 dx = ln |x| + C.
7.
R
Con este formulario resolvemos el problema de cálculo de antiderivadas para muchas funciones.
Y gracias al Teorema Fundamental del Cálculo 1, también seremos capaces de resolver el problema
del cálculo de áreas bajo la gráfica de muchas funciones no sólo de las lineales.
54
R
Ejemplo. Para calcular la integral indefinida 3x2 + 2x − 1dx, utilizamos las fórmulas 1, 2, 3 y 4.
Z
Z
Z
Z
Z
Z
Z
3x2 + 2x − 1dx = 3x2 dx + 2xdx − dx = 3 x2 dx + 2 xdx − dx =
x2+1
x1+1
+2
− x + C = x3 + x2 − x + C
2+1
1+1
d
(x3 + x2 − x + C) = 3x2 + 2x − 1, y observando que
Podemos verificar el resultado derivando dx
obtenemos la función del integrando. Notemos que la fórmula 5 es un resumen de las fórmulas 1, 2,
3, 4. Ası́ por ejemplo
Z
1 4
1 x4+1
x2+1
1 5 2 3
x − 2x2 + 1dx =
−2
+x+C =
x − x + x + C.
2
24+1
2+1
10
3
=3
Ejemplo. La fórmula 4 también puede utilizarse para calcular integrales de potencias fraccionarias
de x por ejemplo
Z
Z
√
1
1
xdx = x1/2 dx = 1
x 2 +1 + C =
+
1
2
1 3/2
2
x + C = x3/2 + C.
3/2
3
Ejemplo. También es posible evaluar integrales indefinidas de funciones exponenciales,
Z
Z
3
3e4x dx = 3 e4x dx = e4x + C
4
=
O una combinación lineal
Z
2e
=2
−x
3
Z
+ 4x dx = 2
e
−x
Z
dx + 4
x3 dx =
x4
1 −x
e + 4 + C = −2e−x + x4 + C
−1
4
.
EJERCICIOS Calcular las siguientes integrales indefinidas:
R
1. 2x5 − 3x2 + x−3 dx
R
2. x2/3 − 4x1/3 + 2x−1/2 dx
R
3. 3.5e−0.5x dx
R
−3
4. 23 e1.4x − 3x2 dx
R
5. x22 + x33 + x4 dx
R
6. (1.192.5x )dx
R −2.1x
7. e 2 dx
√
R
8. √2x + 2x dx
R
9. 4e2.1x+3 dx
R
10. 2x + 2−x dx, Sugerencia: 2x = (eln 2 )x .
R
11. π 2 x + xπ dx
R
12. 2.5(1.60.04x )dx
55
f
4
3
2
1
-2
-1
1
2
x
-1
Figura 3.6: Area bajo la gráfica,
3.3
Rβ
α
f (x)dx
Cálculo de áreas usando integrales
Ahora regresemos al Teorema Fundamental del Cálculo 1 y empleemos la herramienta del cálculo
de integrales definidas para evaluar áreas bajo la gráfica.
Ejemplo. Una población crece a una tasa constante de 1300 individuos por año. Si originalmente
habı́a 50000 individuos. ¿Cuántos individuos habrá dentro de 15 años?
La población que se agrega se calcula mediante
Z 15
1300dx = 1300x |15
0 = 1300(15) − 1300(0) = 19500
0
la cual sumada a los 50000 que habı́a originalmente, da una población total de 50000+19500 = 69500.
Notación. La notación F (x) |βα significa F (β) − F (α).
Ejemplo. Un móvil se desplaza a velocidad constante de 4 m/s. ¿Qué distancia habrá recorrido
después de 45 segundos?
Por supuesto sabemos que la respuesta es distancia = velocidad× tiempo= 4(45) = 90 m. Sin
embargo, empleando la interpretación área bajo la gráfica de la función constante v(x) = 4 se tiene
Z 45
Z 45
distancia recorrida después de 45 s =
v(x)dx =
4dx =
0
0
4x |45
0 = 4(45) − 4(0) = 180
En general, si la velocidad no necesariamente es constante, pero se conoce la velocidad v(x) como
función del tiempo, se puede conocer la distancia recorrida por el móvil como función del tiempo
Z x
distancia recorrida en x segundos = s(x) =
v(t)dt
0
donde la variable ”muda” t se emplea solamente para indicar el proceso de integración.
Ejemplo. La velocidad que recorre una piedra que se deja caer es proporcional al tiempo que lleva
descendiendo desde que se suelta con constante de proporcionalidad 9.8 m/seg 2 , es decir v(x) = 9.8x.
Expresar la distancia que recorre la piedra después de 10 segundos transcurridos desde que se soltó.
Para resolver esta cuestión notamos que la distancia s(x) recorrida por un móvil después de x
segundos se puede determinar si se conoce la velocidad v(x) como función del tiempo. La manera
de hacerlo es evaluando
56
P¢
250
200
150
100
50
-5
0
5
10
15
20
Figura 3.7: Area bajo la gráfica,
t
Z
s(t) =
v(x)dx = 9.8
0
25
R 24
0
30
t
50e.05t dt
t2
+ s0
2
Ejemplo.
Ejemplo. Una población de bacterias se reproduce a una tasa de 50e.05t bacterias/hora, donde t
son las horas transcurridas desde el inicio del experimento. Calcula el incremento de la población
durante 24 horas.
Solución. Como la tasa de incremento de la población es de 50e.05t , el incremento de la población
después de t horas será de
Z t
e.05t t
| = 1000e.05t − 1000
∆P =
50e.05t dt = 50
.05 0
0
sustituyendo t = 24 se tiene
∆P = 2320.12
en particular si originalmente habı́a P0 bacterias se tendrá la siguiente ley de crecimiento para el
cultivo
P (t) = P0 + ∆P = P0 + 1000e.05t − 1000
3.4
Cálculo de probabilidades
El cálculo de áreas se aplican también en la teorı́a de probabilidades. Muchas veces los fenómenos
que estudiamos no se comportan de acuerdo a reglas deterministas. Su evolución se encuentra
influenciada por muchos factores. La probabilidad es una manera de medir la incertidumbre en un
modelo matemático.
Para introducirnos a las nociones básicas de la teorı́a de las probabilidades comenzamos con
algo de terminologı́a. Un experimento (aleatorio) es un procedimiento mediante el cual un
observador al interactuar con un objeto de estudio en ciertas condiciones planificadas, es capaz de
hacer observaciones y registrarlas. Dichas observaciones pertenecen a una colección especı́fica de
posibles resultados. El espacio muestral del experimento es el conjunto S de posibles resultados
cada elemento, s ∈ S de este conjunto se llama punto del espacio muestral. Un evento, E, en el
57
espacio muestral es un subconjunto del espacio muestral, E ⊂ S que el observador puede seleccionar
prescribiendo algunas especificaciones. El evento cierto corresponde a todo el espacio muestral S,
el evento vacı́o corresponde al evento que no tiene ningún punto y se designa ∅. El evento que consta
de un sólo punto s ∈ S del espacio muestral se designa como evento simple y se denota E = {s}.
Dos eventos E, E 0 son disjuntos si no hay eventos simples s ∈ E de uno de ellos, que estén en el
otro E 0 .
Una variable aleatoria continua X es la regla de asignación, que a cada punto del espacio
muestral le asigna un valor numérico real, y a cada evento le asigna un intervalo (o una colección de
intervalos, dentro de la recta numérica R. Al evento cierto le asigna el intervalo −∞ < X < +∞.
En general, una variable aleatoria continua X permite designar un evento mediante una colección
de intervalos de la forma:
a ≤ X ≤ b, a < X ≤ b, a ≤ X < b, a < X < b, donde a < b
O también intervalos de la forma:
X > a, X ≥ a, x < b, X ≤ b.
Ejemplo. En un cultivo de células se elige una al azar y se determina mediante un procedimiento
especı́fico la edad de la misma, medida en horas. En este caso el experimento es elegir al azar una
célula del cultivo. El espacio muestral consta de la colección de todas las células del cultivo, alguna
de las cuales puede ser seleccionada al momento de la medición. La variable aleatoria es la asignación
de la edad de la célula una vez que se ha seleccionado al azar una de ellas.
Como ejercicio determina en el ejemplo anterior cuál es el evento cierto y el evento vacı́o.
Una probabilidad P para una variable aleatoria continua X asociada a un experimento dado,
es una regla de asignación que a cada intervalo, digamos a < X ≤ b, le asigna un número real
P (a < X ≤ b) entre 0 y 1.
En un modelo probabilista 0 ≤ P (a < X ≤ b) designa la certidumbre que tenemos (medida en
porcentaje) de que una vez hecha la observación obtengamos un valor de la variable aleatoria entre
a y b.
Ejemplo. Se selecciona al azar una lámpara incandescente de una fábrica y se quiere saber la
probabilidad de que su vida útil ”esté entre” 500 y 1000 horas. Si X es la variable aleatoria continua
que mide la vida útil de una bombilla seleccionada al azar en una fábrica, lo que deseamos saber es
el valor de P (500 < X ≤ 1000). Si por otro lado nos preguntaran cuál es la probabilidad de que
dicha bombilla tenga una vida útil de ”al menos” 100 horas, entonces dicha pregunta se traduce a
determinar P (X ≥ 100) es decir P (100 ≤ X < +∞)
La probabilidad P para una variable aleatoria continua X debe satisfacer ciertas propiedades
que aseguran que se trata de una medida de certidumbre:
1. La probabilidad de un evento es no negativa, es decir P (a < X ≤ b) ≥ 0.
2. La probabilidad del evento cierto que corresponde a todos los posibles valores de la variable
aleatoria es 1, es decir P (−∞ < X < +∞) = 1.
3. La probabilidad de dos eventos disjuntos es la suma de las probabilidades de cada uno de ellos,
ası́ por ejemplo, se puede deducir que:
P (X > a) = 1 − P (X ≤ a)
P (a < X ≤ b) = P (X ≤ b) − P (X ≤ a)
58
Observación. Anteriormente usábamos el cálculo como herramienta para desarrollar modelos deterministas de un fenómeno. Es decir, querı́amos determinar o bien estudiar las propiedades de
una función f (x). Dicha función determinaba completamente el comportamiento de una variable
dependiente y = f (x) que era de nuestro interés a partir de una variable independiente x.
En contraste, en los modelos probabilistas, nuestro interés en determinar cuál es la probabilidad
P (a < X ≤ b) en el contexto de un experimento aleatorio, ası́ como las propiedades de dicha
probabilidad. En este caso, la probabilidad expresa la certidumbre de observar el evento en cuestión.
Ahora veamos como el cálculo también es útil para estudiar modelos probabilistas. Especı́ficamente
la integral definida resulta útil para expresar la probabilidad P asociada a una variable aleatoria X
en un experimento.
La idea central es que medir la certidumbre de un evento y medir el área de una región (hablamos
del área bajo la gráfica) son dos procedimientos análogos. Ası́ que estudiar las propiedades de la
probabilidad corresponde a estudiar las propiedades del área.
Para aclarar esta idea comenzamos con expresar la probabilidad P como un área bajo la gráfica.
Definición. Una función de densidad de probabilidad para una variable aleatoria continua X
con probabilidad P , es una función p(x), que satisface las siguientes condiciones:
1. Es una función no negativa, es decir p(x) ≥ 0.
2. Es una función de área bajo la gráfica total unitaria, es decir
R +∞
−∞
p(x)dx = 1.
3. La probabilidad de que la variable aleatoria X adquiera valores en el intervalo comprendido
entre a y b, es el área bajo la gráfica de p(x), es decir
b
Z
P (a < X ≤ b) =
p(x)dx
a
En particular las probabilidades asociadas a los intervalos X ≤ b se expresarı́a en términos de la
función de densidad de probabilidad como
Z
b
P (X ≤ b) =
p(x)dx
−∞
Rb
Ra
donde −∞ p(x)dx se aproxima tomando áreas bajo la gráfica −N p(x)dx en el intervalo −N ≤ x ≤ b
con −N cada vez más negativo. Es decir
Z
b
Z
p(x)dx =
−∞
b
lim
−N →−∞
p(x)dx
−N
y análogamente,
Z
P (X ≥ a) =
+∞
p(x)dx.
a
Observación. Un modelo determinista se especifica mediante una función f (x) que relaciona la
variable dependiente con la variable independiente. Un modelo probabilista asociado a un experimento se especifica mediante una función de densidad de probabilidad apropiada para la variable
aleatoria de interés.
59
pHxL
0.12
0.10
0.08
0.06
0.04
0.02
-5
0
5
10
15
x
Figura 3.8: Función de densidad uniforme en , 0 ≤ X ≤ 10
Ejemplo. En una parada del transporte público los autobuses que pasan por ahı́ lo hacen cada 10
minutos. Sea X la variable aleatoria que mide el tiempo de espera que le toma a una persona que
arriba aleatoriamente a la parada, para subir al autobús siguiente.
Notemos que todos los posibles valores de la variable aleatoria X están comprendidos en el
intervalo 0 < X ≤ 10. Es decir, el intervalo 0 < X ≤ 10 corresponde a todo el espacio muestral S,
y en consecuencia P (0 < X ≤ 10) = 1.
Observemos también que todos los posibles valores dentro del intervalo 0 < X ≤ 10 son igualmente probables, ya que la persona llega a la parada aleatoriamente, no ha planeado llegar justo
cuando pasa el autobús. En este caso la función de densidad permanece constante
p(x) = k
Para identificar el valor de la constante k, calculamos la probabilidad del evento cierto tendremos
Z +∞
Z 10
Z 10
1=
p(x)dx =
p(x)dx =
kdx = k · 10
−∞
0
0
de donde k = 1/10
por lo tanto
Z
P (a < X ≤ b) =
a
b
b−a
1
dx =
10
10
es la probabilidad de que una persona espere entre a y b minutos antes de subir al autobús.
Por ejemplo, la probabilidad de que una persona tarde al menos 3 minutos en la parada es
P (X ≥ 3) = P (3 ≤ X ≤ 10) = 7/10, que corresponde a una probabilidad del 70 %.
Una variable aleatoria que toma valores en un intervalo A ≤ X ≤ B, y para la que los posibles
valores tienen la misma probabilidad de ocurrir, se dice que es uniformemente distribuida. Para
1
, es
calcular la probabilidad de un evento utilizamos función de densidad uniforme, p(x) = B−A
decir,
Z b
b−a
P (a ≤ X ≤ b) =
p(x)dx =
.
B−A
a
Una variable aleatoria se dice exponencialmente distribuida si tiene función de densidad
exponencial con valor esperado λ > 0,
1 −x/λ
, si x ≥ 0
λe
p(x) =
0,
si x < 0
60
pHxL
0.25
0.20
0.15
0.10
0.05
-2
0
2
4
6
8
10
12
x
x
Figura 3.9: Función de densidad exponencial 15 e− 5 .
-2
pHxL
0.25
pHxL
0.25
0.20
0.20
0.15
0.15
0.10
0.10
0.05
0.05
0
2
4
6
8
10
12
x
-2
0
2
4
6
8
10
12
x
Figura 3.10: Probabilidad P (X ≥ 7) y P (2 ≤ X ≤ 5), para la función de densidad exponencial
1 −x
5.
5e
Ejemplo. El tiempo de supervivencia de un paciente que se somete a un tratamiento quı́mico es
una variable aleatoria con distribución exponencial. Supongamos que en un tratamiento especı́fico
se tiene un tiempo esperado de supervivencia de λ = 5 años. Determina la probabilidad de que un
paciente sobreviva al menos 2 años y no más de 5. Determina la probabilidad de que un paciente
sobreviva más de 7 años.
Solución. La probabilidad se calcula como
Z
b
P (a ≤ X ≤ b) =
a
1
a
b
1 −x
e 5 dx = −e− 5 x |ba = e− 5 − e− 5
5
por lo tanto P (2 ≤ X ≤ 5) = e−2/5 − e−5/5 = 0.67032 − 0.367879 = .3024 que corresponde a una
probabilidad de 30.24 %, sobrevivir al menos 2 años y no más de 5.
Por otro lado, la probabilidad de sobrevivir al menos de 7 años serı́a
Z
P (X > 7) = P (7 < X < ∞) =
7
+∞
1 −x/5
e
dx = e−7/5 − lim e−N/5 = e−7/5 = .04931
N →∞
5
lo cual corresponde a una probabilidad de 4.93% de sobrevivencia de al menos 7 años.
61
0.4
0.3
0.2
0.1
-4
-2
2
4
Figura 3.11: Curvas de distribución normal para a) µ = 0, σ = 1; b) µ = 0, σ = 3; c) µ = 2, σ = 1.
En este ejemplo hemos visto que es necesario saber que e−x se aproxima a 0 cuando x → +∞,
para determinar las fórmulas generales para el cálculo de probabilidades de variables aleatorias
exponencialmente distribuidas:
P (a < X ≤ b) =
e−a/λ
e−b/λ
−
.
a
b
P (X ≥ a) =
e−a/λ
a
Otra función de densidad muy útil es la función de densidad normal. Dicha función está
determinada por dos parámetros que se llaman: el ”valor esperado” µ y ”desviación estándar” σ > 0,
y tiene como fórmula
1 x−µ 2
1
p(x) = √ e− 2 ( σ )
σ 2π
De esta manera, una variable aleatoria continua X está normalmente distribuida si las probabilidades de eventos se calculan a través de la fórmula de integración
b
Z
√
P (a < X ≤ b) =
a
1 x−µ 2
1
e− 2 ( σ ) dx
2πσ
Muchas variables aleatorias se distribuyen normalmente o aproximadamente normales: estatura,
peso, concentración de un cierto contaminante en la sangre, esperanza de vida, coeficiente de inteligencia, número de palabras que una persona al azar puede memorizar en un lapso de tiempo,
calificaciones en exámenes.
La gráfica de p(x) tiene forma de campana centrada en µ, dependiente de los valores de σ > 0
puede ser más ancha o angosta. Para µ = 0, σ = 1 la campana se llama curva normal tı́pica,
2
corresponde a la gráfica de p(x) = √12π e−x /2 .
R
2
Desafortunadamente no es posible calcular la integral indefinida e−x /2 dx mediante técnicas de
integración que nos proporcionen un fórmula en términos de funciones conocidas: polinomios, radicales, exponenciales, logaritmos, trigonométricas, etc. Esto no significa que no existe la antiderivada,
lo que significa es que no podemos darle una fórmula a través de alguna técnica de integración.
Para salvar esta dificultad, el área bajo la gráfica se calcula mediante métodos numéricos, implementados en programas de cómputo y/o tablas.
62
0.4
0.3
0.2
0.1
-4
-2
2
4
Figura 3.12: Area de ”colas hacia la izquierda” en la distribución normal tipificada (P (Z ≤ 1)).
Las tablas usualmente contienen las áreas bajo la gráfica de una variable Z con distribución
normal tipificada, de ”colas hacia la izquierda”, es decir, contienen los valores
Z z
2
1
P (Z ≤ z) = √
e−x /2 dx.
2π −∞
Ejemplo. En una fábrica de termómetros se tiene que los termómetros no están correctamente
calibrados. La temperatura que marca un termómetro tomado al azar en el punto de congelación
de agua (0o centı́grados) es una variable aleatoria Z normalmente distribuida. Supongamos además
que tiene distribución normal tipificada, con µ = 0o C y σ = 1o C. Entonces, la probabilidad de que
un termómetro tomado al azar marque a lo más 1o en el punto de congelación del agua es
P (Z ≤ 1) = .8423
Lo que indica una probabilidad de 84.13%.
Para las variables aleatorias continuas con las tres distribuciones que hemos analizado se tienen
las siguientes fórmulas que se deducen de los teoremas de integración:
P (X < b) = P (X ≤ b)
P (a < X) = P (a ≤ X)
P (a < X < b) = P (a ≤ X < b) = P (a < X ≤ b) = P (a ≤ X ≤ b).
Y también las siguientes fórmulas:
P (a ≤ Z ≤ b) = P (Z ≤ b) − P (Z ≤ a).
P (Z > a) = 1 − P (Z ≤ a).
que resultan útiles para el cálculo de probabilidades en la distribución normal tipificada usando
tablas:
EJERCICIOS
1. Supón que el tiempo de espera en la fila de un banco es una variable aleatoria con distribución
exponencial y función de densidad de probabilidad p(x) = 61 e−x/6 , para x ≥ 0, donde x es el
número de minutos que un cliente seleccionado al azar espera en la fila antes de ser atendido.
Calcula cuál es la probabilidad de que un cliente seleccionado al azar permanezca:
63
(a) Al menos 2 minutos en la fila.
(b) A lo más 3 minutos en la fila.
(c) Al menos 1 minuto y a lo más 10 minutos en la fila.
2. La hora de la noche en la que cierta especie de depredador que vive en una zona de cultivo
sale de su guarida. Supongamos que es una variable aleatoria uniformemente distribuida con
valores 6pm ≤ X ≤ 6am determina la probabilidad de que:
(a) El depredador salga a más tardar a las 8 pm.
(b) El depredador salga después de las 12 am.
(c) El depredador no salga en toda la noche.
(d) El depredador salga en algún momento de la noche.
(e) El depredador salga después de las 12:30 am y a más tardar a la 1pm.
3. Utilizando la tabla de la distribución normal tipificada calcula las siguientes probabilidades
(a) P (Z > 2).
(b) P (Z ≤ −3).
(c) P (−1 < Z < 3.1).
(d) P (0.2 < Z ≤ 1.87).
(e) P (Z ≤ −1.87).
3.5
Ejercicios de repaso
1. Se tomaron las siguientes mediciones en el velocı́metro de un automóvil cada media hora
obteniéndose la gráfica es 3.13, calcula la distancia recorrida.
v-
km
hr
100
80
60
40
20
1
2
3
4
5
t - hr
Figura 3.13: Gráfica de la velocidad en el problema 1
2. La actividad biológica en un estanque se refleja en la rapidez con la que el CO2 entra al agua.
A los biólogos les interesa la rapidez neta con la que el dióxido de carbono sale o entra. Se
estimó que en un estanque la rapidez en milimoles de CO2 por litro y por hora, está dada por
el modelo
r(x) = .01931x(x − 12.5)2 − 3
donde r es la rapidez (en mmol/lt · min) y x es el tiempo transcurrido en horas.
(a) Esboza la gráfica de r(x) en el intervalo x ∈ [0, 15] usando x = 0, 1, 2, ..., 15.
(b) ¿Para qué valores aproximados de x se tiene que r es cero?
64
(c) Usando los valores en (b)¿En qué intervalo (a, b) se tiene una razón r(x) negativa? ¿Cuál
es la interpretación biológica de este hecho?
(d) Calcula la cantidad de CO2 que entró al estanque en el intervalo [0, 15].
3. Una población animal se reproduce con una rapidez o razón de crecimiento directamente
proporcional al número de personas presentes en dicho instante. Si la población se duplica en
5 años ¿cuánto tiempo tarda en triplicarse?
4. Sea X la variable aleatoria que mide el lapso de tiempo entre dos avistamientos sucesivos
de murciélagos que polinizan un cultivo de agaves. Supongamos que esté exponencialmente
distribuida con p(x) = 0.3e−0.3x . Si un murciélago acaba de dejar el cultivo de agaves. Calcula
la probabilidad de que el siguiente murciélago llegue:
(a) cuando mucho una hora después.
(b) después de que han transcurrido 3 horas.
(c) después de que han transcurrido 3 horas y cuando mucho 6.
5. El tiempo que un semáforo permanece en rojo es de 40 segundos. Consideramos el tiempo que
un conductor permanece esperando a que el semáforo le dé el siga una vez que se detuvo. Se
trata de una variable aleatoria uniformemente distribuida con valores 0 ≤ X ≤ 40 segundos.
Calcula la probabilidad de que el conductor espere:
(a) A lo más 5 segundos.
(b) Al menos 10 y a lo mucho 30 segundos.
(c) A lo mucho 40 segundos.
65
66
Bibliografı́a
[Ha]
Hahn A. Basic Calculus, Springer, 1998.
[HG]
Hughes-Hallet D., Gleason A. Calculus, Wiley, 1994.
[Cl]
Clark C. Mathematical Bioeconomics, 2a. ed., Wiley, 1990.
[HBR]
Hoffmann L., Bradley G., Rosen K. Cálculo Aplicado 8a. ed. McGraw-Hill, 2004.
[St]
H. Steinhaus, Instantáneas matemáticas, Biblioteca Salvat, 1989.
[W]
Wolfram Project http://www.wolfram.com
67