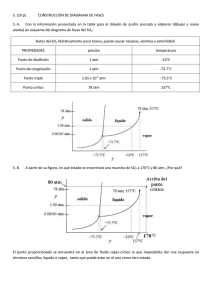
Fuerzas en equilibrio en fluidos
Anuncio

101563_refuerzo 27/2/03 09:35 Página 10 5 Fuerzas en equilibrio en fluidos ACTIVIDADES DE REFUERZO 1. Razona sobre la veracidad o falsedad de las siguientes afirmaciones: a) El empuje que experimenta un balón de fútbol tiene siempre el mismo valor, con independencia del líquido en el que haya sido sumergido. b) Si se tienen dos recipientes con diferentes formas pero con la misma base y se llenan de agua hasta la misma altura (ver dibujo), la presión sobre el fondo será mayor en A, por contener más agua, que en B. A B 2. Determina la presión que ejerce una aguja de 0,5 mm2 de sección sobre una tela al ser empujada con la fuerza de 1 N. Exprésala en pascales y en atmósferas. 3. El Titanic se encuentra hundido a una profundidad de 4 000 m. Determina la presión que soportaría un buzo que llegara al Titanic. Exprésala en unidades del SI y en atmósferas. Dato: densidad del agua del mar = 1 025 kg/m3. 4. Responde a las siguientes cuestiones: a) Explica de forma razonada qué le ocurre a un objeto esférico sumergido en un fluido si su peso es mayor que el empuje, ¿y si es menor que el empuje? b) Si sobre un émbolo de una prensa hidráulica de 40 cm2 ejercemos una fuerza de 15 N, ¿qué masa podrá elevarse con ayuda de dicha prensa si el émbolo grande tiene una superficie de 0,04 m2? c) Explica de forma científica qué ocurre cuando absorbemos el líquido de un vaso con ayuda de una pajita. 5. Si se construyera un barómetro de Torricelli con aceite de densidad 0,8 kg/m3, ¿qué altura mínima debería tener el tubo barométrico si la presión atmosférica en ese punto fuera de 700 mm de Hg? 6. Los submarinos no suelen bajar por debajo de los 50 m de profundidad ya que su estructura no es capaz de soportar la enorme fuerza que ejerce el agua. Calcula el valor de dicha fuerza cuando un submarino de 1 800 m2 de superficie externa se sumerge 50 m en el mar. Dato: densidad del agua del mar = 1 025 kg/m3. 7. Un submarinista debe hacer una descompresión cuando desciende, cada vez que la presión a la que se encuentra sometido varía aproximadamente media atmósfera. Calcula cada cuántos metros debe detenerse para realizar dicha operación. Newton 4.o ESO Actividades de refuerzo 101563_refuerzo 27/2/03 09:35 Página 11 Soluciones 1. a) Falso. El empuje depende de la densidad del fluido desalojado. 5. 700 (mm de Hg) · 1 (atm) = 0,92 atm 760 (mm de Hg) b) Falso. La presión sobre el fondo será la misma, esto se conoce como la “paradoja hidrostática”. 2. 3. 4. 0,92 (atm) · 101 300 (Pa) = 93 196 Pa 1 (atm) El tubo barométrico marca 93 196 Pa. Aplicando la definición de presión: F 1 ( N) P = = = 2 · 106 Pa s 0,5 · 10–6 (m2) 1 (atm) x (atm) = ; x = 19,74 atm 101 300 (Pa) 2 · 106 (Pa) Sabiendo que P = hdg, 93 196 (Pa) = 0,8 (kg/m3) · 9,8 (m/s2) · h h = 11 887,2 m 6. Calculamos la presión a esa profundidad: 3 Hacemos el cambio de unidades: Calculamos el valor de la presión a esa profundidad: P = hdg; P = 50 · 1 025 · 9,8 = 502 250 Pa 2 P = hdg = 4 000 (m) · 1 025 (kg/m ) · 9,8 (m/s ) = = 4,02 · 107 Pa F Como la presión: P = ⇒ F = PS. S 1 (atm) x (atm) = ; x = 397 atm 101 300 (Pa) 4,02 · 108 (Pa) Con los datos que tenemos: F = 502 250 (Pa) · 1 800 (m2) = 9,04 · 108 N Esta fuerza es equivalente al peso en la Tierra de una masa de 90 405 toneladas. a) Si el peso es mayor que el empuje, (aplicando la segunda ley de Newton) el cuerpo se hunde. En caso contrario, el cuerpo sube hasta flotar, en ese instante pasará a estar en equilibrio. b) Por el F1 = S1 principio de Pascal, se cumple que: F2 , sustituyendo: S2 15 (N) F2 – = ; F2 = 150 N. 3 2 4 · 10 (m ) 0,04 (m2) Como nos piden la masa: 7. Como 1 atm son 101 300 Pa, media atmósfera corresponde a 50 650 Pa. De la fórmula de la presión se despeja la altura a la que se produce ese incremento de presión: P 50 650 P = hdg; h = = = 5,04 m dg 1 025 · 9,8 Aproximadamente cada 5 metros hay que hacer una descompresión. 150 = m · 9,8; m = 15,30 kg c) Lo que hacemos es un vacío en el tubo, y la presión atmosférica actúa sobre la superficie libre del líquido provocando el ascenso del líquido por la pajita. Actividades de refuerzo Newton 4.o ESO