TIPOS DE MAQUINAS SIMPLES

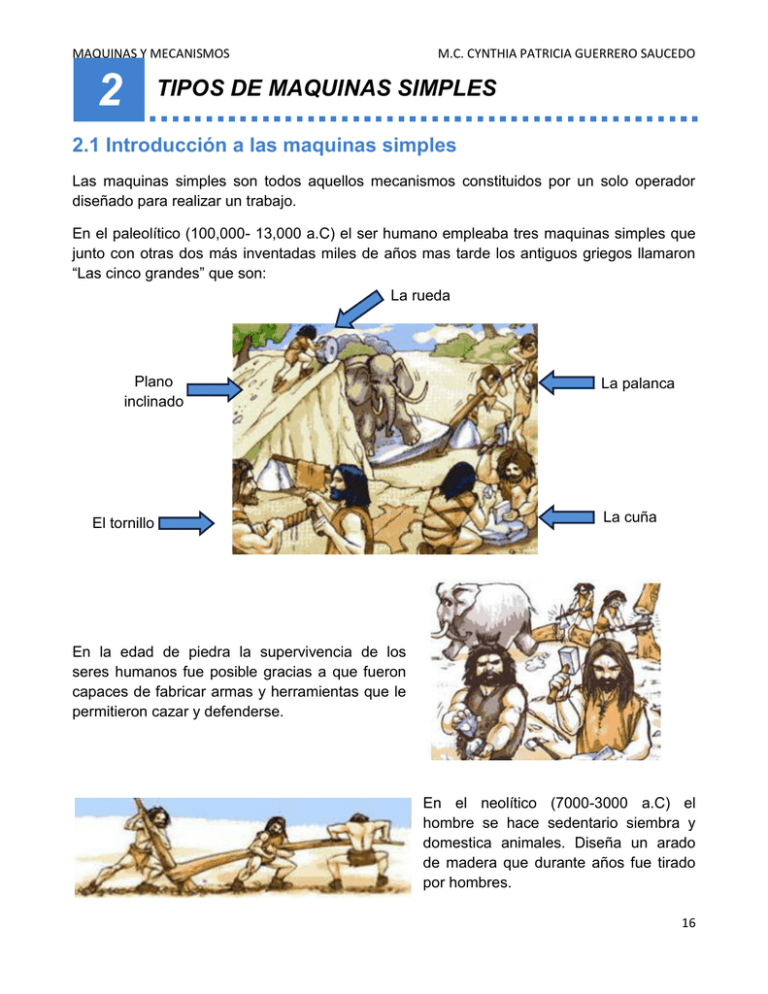
MAQUINAS Y MECANISMOS
2
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
TIPOS DE MAQUINAS SIMPLES
2.1 Introducción a las maquinas simples
Las maquinas simples son todos aquellos mecanismos constituidos por un solo operador
diseñado para realizar un trabajo.
En el paleolítico (100,000- 13,000 a.C) el ser humano empleaba tres maquinas simples que
junto con otras dos más inventadas miles de años mas tarde los antiguos griegos llamaron
“Las cinco grandes” que son:
La rueda
Plano
inclinado
El tornillo
La palanca
La cuña
En la edad de piedra la supervivencia de los
seres humanos fue posible gracias a que fueron
capaces de fabricar armas y herramientas que le
permitieron cazar y defenderse.
En el neolítico (7000-3000 a.C) el
hombre se hace sedentario siembra y
domestica animales. Diseña un arado
de madera que durante años fue tirado
por hombres.
16
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
En la edad de los metales el hombre descubre que cuando
echaba algunos tipos de rocas al fuego salía un liquido
que al enfriarse solidificaba de nuevo.
La metalurgia del hierro inicia hace 4000 años
2.2 La Palanca
La palanca es una máquina simple. Es una máquina porque es capaz de multiplicar la fuerza
y es simple porque está compuesta de muy pocos elementos: una barra rígida y un punto de
apoyo (fulcro). Con una palanca puedo levantar mucho peso haciendo poca fuerza.
La palanca puede
desplazamientos.
emplearse
para
dos
finalidades:
vencer
fuerzas
u
obtener
1. Cuando empleamos la palanca para vencer fuerzas podemos considerar en ella 4
elementos importantes:
Potencia (P), fuerza que tenemos que aplicar.
Resistencia (R), fuerza que tenemos que
vencer; es la que hace la palanca como
consecuencia de haber aplicado nosotros la
potencia.
Brazo de potencia (BP), distancia entre el
punto en el que aplicamos la potencia y el punto
de apoyo (fulcro).
P x BP = R x BR
Brazo de resistencia (BR), distancia entre el
punto en el que aplicamos la resistencia y el
(fulcro).
Ley de la palanca, que dice:
La "potencia" por su brazo es igual a
la "resistencia" por el suyo.
17
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
Ejemplo 2.1: Beto y Ana tienen una masa de 40Kg cada uno. ¿Podrán equilibrarse con el
hipopótamo que pesa 800Kg?
Lo primero que hay que hacer es expresar
la masa en Kg, en peso o fuerza en
newtons:
Rhipopotamo= m∙g=
(800Kg)(9.8m/s2)= 7840N
Pniños= (mbeto+mana)∙g=
(40Kg+40Kg)(9.8m/s2) = 784N
A continuación aplicamos la Ley de la
Palanca: P x BP = R x BR
(784N)(10m)=(7840N)(1m)
7840N=7840N Como los productos son iguales, la palanca se encuentra en equilibrio.
2. Cuando usamos la palanca para generar desplazamiento podemos considerar cuatro
elementos importantes:
Desplazamiento de la potencia (dP), es la
distancia que se desplaza el punto de aplicación
de la potencia cuando la palanca oscila.
Movimiento de la resistencia (dR), distancia
que se desplaza el punto de aplicación de la
resistencia al oscilar la palanca
Brazo de potencia (BP), distancia entre el punto
de aplicación de la potencia y el fulcro.
Brazo de resistencia (BR), distancia entre el
punto de aplicación de la resistencia y el fulcro.
dP
dR
=
BP BR
El desplazamiento de la "potencia" es
a su brazo como el de la "resistencia"
al suyo.
Según los puntos en los que se aplique la potencia (fuerza que provoca el movimiento) y las
posiciones relativas de eje y barra, se pueden conseguir tres tipos diferentes de palancas a
los que se denomina: de primero, segundo y tercer género (o grado).
18
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
2.2.1 Palanca de primer grado
Se obtiene cuando colocamos el fulcro entre la
potencia y la resistencia. La palanca de primer
grado se emplea siempre que queramos
invertir el sentido del movimiento.
Con estas posiciones relativas se pueden
obtener tres posibles soluciones:
1.- Fulcro centrado, lo que implicaría que los brazos de potencia y resistencia fueran
iguales (BP=BR)
Este montaje hace que el esfuerzo y la carga sean iguales (P=R), como también lo serán los
desplazamientos de la potencia y de la resistencia (DP=DR). Es una solución que solamente
aporta comodidad, pero no ganancia mecánica.
Esta disposición se emplea, por ejemplo, en balanzas, sube y baja de los parques
infantiles...
2.- Fulcro cercano a la resistencia, con lo que el brazo de potencia sería mayor que el de
resistencia (BP>BR)
19
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
Esta solución hace que se necesite un menor esfuerzo (potencia) para compensar
la resistencia (P<R), al mismo tiempo que se produce aun mayor desplazamiento de la
potencia que de la resistencia (DP>DR). Este sistema aporta ganancia mecánica y es el
empleado cuando necesitamos vencer grandes resistencias con pequeñas potencias.
Se emplea, por ejemplo, para el movimiento de objetos pesados, balanzas romanas, alicates
de corte, timones de barco...
3.- Fulcro cercano a la potencia, por lo que el brazo de potencia sería menor que el de la
resistencia (BP<BR).
Solución que hace que sea mayor el esfuerzo que la carga (P>R) y, recíprocamente, menor
el desplazamiento de la potencia que el de la resistencia (DP<DR). Esta solución no aporta
ganancia mecánica, por lo que solamente se emplea cuando queremos amplificar el
movimiento de la potencia.
Se utiliza, por ejemplo, en barreras elevables, timones laterales, pinzas de cocina...
20
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
2.2.2 Palanca de segundo grado
Se obtiene cuando colocamos la resistencia entre la potencia y el fulcro. Según esto el brazo
de resistencia siempre será menor que el de potencia, por lo que el esfuerzo (potencia) será
menor que la carga (resistencia).
Esta disposición hace que los movimientos de la potencia y de la resistencia se realicen
siempre en el mismo sentido, pero la carga siempre se desplaza menos que la potencia
(DR<DP), por tanto es un montaje que atenúa el movimiento de la potencia.
Al ser un tipo de máquina cuya principal ventaja es su ganancia mecánica, su utilidad
principal aparece siempre que queramos vencer grandes resistencias con pequeñas
potencias, como ejemplos se puede citar el cascanueces, la carretilla o la perforadora de
hojas de papel, cortaúñas, remos,....
2.2.3 Palanca de tercer grado
Se obtiene cuando ejercemos la potencia entre el fulcro y la resistencia. Esto tras consigo
que el brazo de resistencia siempre sea mayor que el de potencia, por lo que el esfuerzo
siempre será mayor que la carga (caso contrario al caso de la palanca de segundo grado).
21
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
Esta disposición hace que los movimientos de la potencia y de la resistencia se realicen
siempre en el mismo sentido, pero la carga siempre se desplaza más que la potencia
(DR>DP).
Al ser un tipo de máquina que no tiene ganancia mecánica, su utilidad práctica se centra
únicamente en conseguir grandes desplazamientos de la resistencia con pequeños
desplazamientos de la potencia. Ejemplos típicos de este tipo de palanca son las pinzas de
depilar, las paletas y la caña de pescar. A este tipo también pertenece el sistema motriz del
esqueleto de los mamíferos.
2.2.4 Palancas articuladas
Uniendo varias palancas con uniones móviles se construyen
mecanismos complejos que pueden realizar funciones más
complicadas, como la del vehículo elevador de la derecha. El
cuerpo humano también es un conjunto de palancas acopladas,
donde las barras son los huesos, los músculos ejercen la fuerza y
las articulaciones son las uniones móviles.
El cierre de las dos palancas articuladas de la base obliga a que
el resto de palancas se cierren. Esto produce el desplazamiento
en vertical del conjunto, que alcanza gran altura.
22
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
Actividad 1
Resuelve los siguientes problemas:
1. El mecanismo de la figura debe levantar
el peso de 4 toneladas. Calcular la fuerza
que se debe ejercer sobre el embolo para
lograrlo.
(Recuerda que para pasar de masa (Kg) a
fuerza (N) deberás utilizar la formula F=mg)
¿Que tipo de palanca es?
2. ¿Que fuerza debemos utilizar para
levantar la carrucha?
(Recuerda que para pasar de masa (Kg) a
fuerza (N) deberás utilizar la formula F=mg)
¿Que tipo de palanca es?
Omar (60Kg)
María (20Kg)
3. ¿A que distancia del punto de apoyo
deberá colocarse María para equilibrar el
columpio con su hermano Omar?
(Recuerda que para pasar de masa (Kg) a
fuerza (N) deberás utilizar la formula F=mg)
1m
¿?
4. El elefante pesa 300Kg y la longitud del
brazo donde se apoya es de 50cm y la
hormiga pesa 1g. ¿Que longitud deberá
tener el brazo donde se apoya la hormiga
para que pueda levantar al elefante?
(Recuerda que para pasar de masa (Kg) a
fuerza (N) deberás utilizar la formula F=mg)
3. El pez que estira de esta caña de pescar
hace una fuerza de 30N. ¿Que fuerza será
necesario aplicar para extraerlo del agua?
¿Que tipo de palanca es?
50 cm
2m
23
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
Actividad 2
Debajo de cada imagen escribe el grado de palanca al que pertenece y marca sobre cada
imagen la letra F en donde se encuentre el Fulcro, P donde se aplique la potencia y R
donde se tenga la Resistencia:
24
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
2.3 El plano inclinado
El plano inclinado es una rampa que sirve para elevar cargas realizando menos esfuerzos.
En la siguiente figura vemos que con la rampa los chicos pueden subir al hipopótamo
haciendo menos fuerza de lo que pesa. Cuanto menos inclinada este la rampa, menos será
la fuerza que tendrá que hacer, pero entonces recorrerán una distancia mayor para subir la
misma altura.
F=
Ra
b
F= fuerza [N]
R= peso del
hipopótamo [N]
a= altura [m]
b= distancia recorrida
[m]
1N=(1Kg)(9.8m/s2)
Ejemplo: si yo peso 70Kg ¿a cuántos Newtons equivale?
70Kg×9.80665 m/s2 = 686 N
Si se quiere elevar una altura al hipopótamo, los chicos tendrán que tirar de la cuerda con
una fuerza F, que siempre será menor que el peso R.
Ejemplo 2.2: ¿Cuál sería la fuerza necesaria para mover al hipopótamo hasta la parte
superior de la rampa si el peso del hipopótamo es de 8,000N, la altura de la rampa es de 1m
y la distancia recorrida es de 2m?
F= ?
R= 8,000N
a= 1m
b= 2m
25
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
Ejemplo 2.3: ¿Qué fuerza necesita aplicar un individuo para subir una carreta a un
camión, si la carreta pesa 1,500N por un plano inclinado de 3m de longitud colocado a una
altura de 2m?
F= ?
R= 1,500N
a= 2m
b= 3m
Ejemplo 2.4: Si la fuerza necesaria para subir un barril a una troca es de 284N, la altura
de la rampa es de 1.5m y la distancia a recorrer es de 2.7m ¿Cuánto pesa el barril?
F= 284N
R= ?
a= 1.5m
b= 2.7m
Despejamos R y nos queda:
Ejemplo 2.5: Calcula la distancia a recorrer en la rampa si hay que subir un barril de
71Kg, la altura de la rampa es de 2.4m y la fuerza aplicada es de 435N.
F= 435N
Peso del
barril= 71Kg
a= 2.4m
b= ?
Primero convertimos el peso del barril en newtons
R=(71Kg)(9.8m/s2)= 695.8N
Despejamos b y nos queda:
=
∙a
=
)
m)
=
m
26
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
Actividad 3
Resuelve los siguientes problemas:
1. Cuál sería la fuerza [N] necesaria para subir una caja a un camión, si la caja pesa 725N
, la altura de la rampa es de 1.2m y la distancia a recorrer es de:
a) 2.2m
b) 3.5m
2. Calcula el peso de un carrito de mandado [Kg] si la altura de la rampa es de 80cm, la
distancia a recorrer es de 2.32m y la fuerza necesaria para subir el carrito es de:
a) 320N
b) 450N
3. Cuál sería la fuerza necesaria [N] para subir un vagón en la montaña rusa si el vagón
pesa 850Kg, la distancia a recorrer es de 75m y la altura es de
a) 38m
b) 45m
2.4 La cuña
La cuña es un plano inclinado doble, donde la fuerza que se aplica
perpendicular a la base se transmite multiplicada a las caras de la
cuña. La fuerza aumenta más cuanta mayor longitud tienen las caras
y menor longitud tiene la base.
La cuña se utiliza en hachas, cuchillos, cinceles, arados, rompehielos,
etc.
Cuña
hacha
arado
rompehielos
27
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
2.5 El tornillo
El tornillo es un plano inclinado, pero enrollado sobre un cilindro. Cuando se aplica presión
y se enrosca, se multiplica la fuerza aplicada. Cada filete de la rosca hace de cuña,
introduciéndose en el material con poco esfuerzo.
En él se distinguen tres partes básicas: cabeza, cuello y rosca:
La cabeza permite sujetar el tornillo o imprimirle un movimiento giratorio con la ayuda de
útiles adecuados; el cuello es la parte del cilindro que ha quedado sin roscar (en algunos
tornillos la parte del cuello que está más cercana a la cabeza puede tomar otras formas,
siendo las más comunes la cuadrada y la nervada) y la rosca es la parte que tiene tallado el
surco. Además cada elemento de la rosca tiene su propio nombre; se denomina filete o hilo a
la parte saliente del surco, fondo o raíz a la parte baja y cresta a la más saliente.
El tornillo se utiliza en escaleras de caracol, carreteras, saca corcho, llaves de agua, resorte,
tornillos, gato de tornillo, etc.
Tornillo de Arquímedes utilizado para sacar agua
28
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
2.6 El torno
El torno es una maquina simple, está formado por un cilindro horizontal de radio (r), que gira
sobre un eje.
Ese cilindro se puede hacer girar a través de una manivela con radio de giro (R) mayor al
radio del cilindro al aplicar una fuerza (F), que hace enrollar una cuerda en el cilindro
subiendo la carga (C) sostenida en el otro extremo. Este tipo de maquinas simples se
emplea generalmente para sacar agua de los pozos.
F
FR=Cr
Manivela
F= fuerza [N]
R= radio de giro de la
manivela [cm]
r= radio del cilindro [cm]
C= peso de la carga
[N,Kg]
Ejemplo 2.6: ¿Que fuerza [N] se necesita aplicar a un torno, si el radio del cilindro es de 7
cm y el que describe la manivela es de 25 cm, la carga es de 250 N?
F= ?
r= 7cm
R= 25cm
C= 250N
FR=Cr
Despejamos F y nos queda:
r
=
=
(
)( cm)
=
cm
Ejemplo 2.7: Un torno dispone de un cilindro para enrollar el cable con un diámetro de
40cm y con una manivela cuyo radio es de 1m. Si aplicamos 300Kg sobre la manivela del
torno, ¿Cual es la carga máxima [Kg] que es capaz de elevar?
300Kg
r= 40cm
R= 1m
C= ?
Primero convertimos los 300Kg que se aplican al torno en Fuerza [N] con
la siguiente formula F=mg
F=(300Kg)(9.8m/s2)=2,940N
De la formula:
FR=Cr
29
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
Despejamos C y nos queda:
(
)(
cm)
=
=
=
r
cm
Como la carga esta en terminos de la fuerza y es de 7,350N, hay que
convertirla en masa para conocer su valor en Kg.
Utilizamos la formula F=mg donde F corresponde al peso de la carga en
Newtons, m es el peso de la carga el Kg y g es la gravedad.
Despejamos m, m=F/g y nos queda
m=(7,350N)/(9.8m/s2)= 750Kg
Por lo cual, la carga máxima que es capaz de elevar el torno es de
750Kg.
Actividad 4
Resuelve los siguientes problemas:
1. ¿Que fuerza [N] se necesita aplicar a un torno, si el radio del cilindro es de 15 cm y el
que describe la manivela es de 30 cm, la carga es de 148 kg?
2. Un torno dispone de un cilindro para enrollar el cable con un diámetro de 33 cm y con
una manivela cuyo radio es de 60cm. Si aplicamos 184Kg sobre la manivela del torno,
¿Cual es la carga máxima [Kg] que es capaz de elevar?
30
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
2.7 Poleas y polipastos
Para levantar una carga se puede hacer tirando de ella hacia arriba pero suele ser incómodo
y está limitada la altura de elevación.
La polea es una rueda con una hendidura en la llanta por donde se introduce una cuerda o
una correa.
Las poleas sirven para elevar cargas con más comodidad porque cambian la dirección de la
fuerza. Pero lo más importante es que también se puede dividir la fuerza para elevar una
gran carga si se combinan las poleas formando un polipasto.
Un polipasto es un conjunto de poleas combinadas de tal forma que puedo elevar un gran
peso haciendo muy poca fuerza.
Un polipasto está compuesto de una polea fija y una polea móvil. La polea fija solo gira
cuando se tira de la cuerda y la polea móvil gira a la vez que se desplaza hacia arriba. En las
ilustraciones podemos entender cómo es posible disminuir la fuerza aplicada empleando
poleas fijas y móviles.
2.7.1 Polea fija
Para elevar la carga, la fuerza que se ejerce tiene que ser mayor o igual que la resistencia.
En este caso, la polea gira pero sin moverse de su sitio, es una polea fija.
F=R
F= ?
F= fuerza [N]
R= resistencia [N, Kg]
Ejemplo 2.8: ¿Cuánta fuerza [N] necesita aplicar el hipopótamo a la polea para levantar a
los dos niños que están en la canasta y que ejercen una resistencia de 800N?
R=800N
F= ?
F=R
F=800N
31
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
La encontramos en mecanismos para el accionamiento de puertas
automáticas, sistemas de elevación de cristales de automóviles,
ascensores, tendales, poleas de elevación de cargas, posos, etc.
2.7.2 Polea móvil
Una polea móvil divide por dos la fuerza realizada, pero es necesario recoger el doble de
cuerda.
F=R/2
F= ?
F= fuerza [N]
R= resistencia [N, Kg]
Ejemplo 2.9: ¿Cuánta fuerza [N] necesita aplicar el hipopótamo a las poleas fija y movil
para levantar a los dos niños que están en la canasta y que ejercen una resistencia de
800N?
R=800N
F= ?
F=R/2
F=800N/2= 400N
En este caso, el peso cuelga de la polea móvil, y se reparte entre las dos cuerdas; es decir,
la mitad de peso lo soporta el tronco y la otra mitad el hipopótamo.
32
MAQUINAS Y MECANISMOS
M.C. CYNTHIA PATRICIA GUERRERO SAUCEDO
2.7.3 Polipasto
Con ocho poleas móviles se divide por dieciséis la fuerza a cambio de recoger dieciséis
veces más longitud de cuerda.
F=R/2n
F= fuerza [N]
F= ?
R= resistencia [N, Kg]
N= numero de poleas
móviles
Ejemplo 2.10: ¿Cuánta fuerza [N] necesitan aplicar dos ni;os al polipasto compuesto por
8 poleas moviles para levantar a un hipopotamo que ejercen una resistencia de 8000N?
R=8000N
n=8
F= ?
F=R/(2n)
F=800N/(2x8)= 500N
En este caso, los chicos podrán levantar al hipopótamo realizando un esfuerzo de 500N
(como si levantaran 50 kg).
Actividad 5
Resuelve los siguientes problemas:
1. ¿Qué fuerza es necesario aplicar para levantar una carga de 50 Kg con una polea fija?
2. ¿Qué fuerza es necesario aplicar para levantar una carga de 50 Kg con una polea
móvil?
3. ¿Qué fuerza es necesario aplicar para levantar una carga de 50 Kg con un polipasto
compuesto por 6 poleas móviles?
33