Tarea

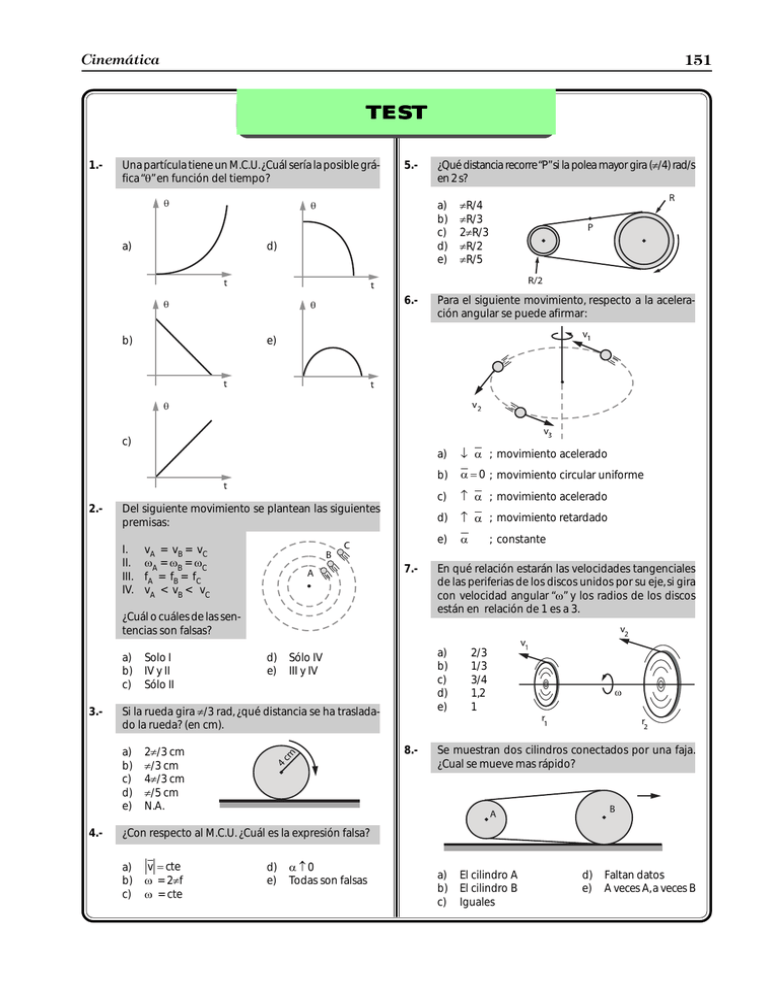
Cinemática
151
TEST
1.-
Una partícula tiene un M.C.U. ¿Cuál sería la posible gráfica “θ” en función del tiempo?
a)
5.-
a)
b)
c)
d)
e)
d)
6.-
b)
¿Qué distancia recorre “P” si la polea mayor gira (π/4) rad/s
en 2 s?
Para el siguiente movimiento, respecto a la aceleración angular se puede afirmar:
e)
c)
2.-
Del siguiente movimiento se plantean las siguientes
premisas:
I.
II.
III.
IV.
vA = vB = vC
ωA = ωB = ωC
fA = fB = fC
vA < vB < vC
7.-
¿Cuál o cuáles de las sentencias son falsas?
a)
b)
c)
3.-
4.-
Solo I
IV y II
Sólo II
d)
e)
8.-
2π/3 cm
π/3 cm
4π/3 cm
π/5 cm
N.A.
a)
Bα
b)
α = 0 ; movimiento circular uniforme
c)
; movimiento acelerado
d)
Aα
Aα
e)
α
; constante
; movimiento acelerado
; movimiento retardado
En qué relación estarán las velocidades tangenciales
de las periferias de los discos unidos por su eje, si gira
con velocidad angular “ω” y los radios de los discos
están en relación de 1 es a 3.
a)
b)
c)
d)
e)
Sólo IV
III y IV
Si la rueda gira π/3 rad, ¿qué distancia se ha trasladado la rueda? (en cm).
a)
b)
c)
d)
e)
πR/4
πR/3
2πR/3
πR/2
πR/5
2/3
1/3
3/4
1,2
1
Se muestran dos cilindros conectados por una faja.
¿Cual se mueve mas rápido?
¿Con respecto al M.C.U. ¿Cuál es la expresión falsa?
a)
b)
c)
v = cte
ω = 2πf
ω = cte
d)
e)
α≠0
Todas son falsas
a)
b)
c)
El cilindro A
El cilindro B
Iguales
d)
e)
Faltan datos
A veces A, a veces B
Jorge Mendoza Dueñas
152
9.-
En un M.C.U. respecto a la aceleración, señalar verdadero (V) ó Falso (F).
I.
II.
III.
a)
b)
c)
10.-
No posee ningún tipo de aceleración.
La aceleración tangencial es cero.
Posee aceleración angular.
FFF
VFV
FVF
d)
e)
VFF
VVV
Una rueda gira a razón de 180 revoluciones por minuto, su velocidad angular en rad/s es:
a)
4π
b)
6π
c)
8π
d)
π
e)
10π
PROBLEMAS RESUEL
TOS
RESUELTOS
A
1.-
problemas de aplicación
Una partícula describe una circunferencia de radio igual
a 30 cm y da 4 vueltas en 20 segundos; calcular:
a)
b)
c)
3.-
Solución:
El período
La frecuencia
La velocidad angular
o Velocidad angular del horario
Solución:
a)
T=
Tiempo total
# de vueltas
20
T=
4
b)
⇒
2π
5
ω=
π
rad / h
6
ω=
f = 0 , 2 Hz
⇒
ω=
2π rad
12 h
Ángulo recorrido
Tiempo empleado
⇒
ω=
2π rad
1h
ω = 2π rad / h
4.⇒
Ángulo recorrido
Tiempo empleado
o Velocidad angular del minutero
2π
ω=
T
ω=
2.-
4
20
ω=
T = 5s
# de vueltas
f=
Tiempo total
f=
c)
⇒
En un reloj de agujas, determinar la velocidad angular
del horario y minutero, en rad/h.
ω = 0 , 4 π rad / s
Un auto va a 80 km/h, el diámetro de la llanta es de
33 cm. Calcular la velocidad angular.
Solución:
Considerando que el período de la Luna alrededor de
la Tierra es 28 días. Determinar la velocidad angular
de la Luna respecto de la Tierra en rad/h.
o v = 80 km / h =
200
m/ s
9
o Cálculo de la velocidad angular: v = ωR
Solución:
o TLuna = 28 días
⇒
200
= ω 0 , 33
9
b g
24 h
TLuna = 28 días ×
1día
ω=
TLuna = 672 h
o Calculando la velocidad angular: ω =
ω=
2π
672
⇒
ω=
π
rad / h
336
2π
T
5.-
200
rad / s
297
Una rueda durante su recorrido necesita 3 s para girar
un ángulo de 234 radianes; su velocidad angular al
cabo de este tiempo es de 108 rad/s. Determinar su
aceleración angular constante.
Cinemática
153
Solución:
2.-
Un cono gira con período de 4 s. ¿En qué relación están las velocidades lineales de los puntos P y Q?
o Datos:
t = 3s
ω F =108 rad / s
θ = 234 rad
α=?
o Calculando la velocidad angular inicial:
FG ω + ω IJ t
H 2 K
F ω + 108 IJ 3
234 = G
H 2 K
θ=
o
F
o
⇒ ω o = 48 rad / s
Solución:
o Calculando la aceleración angular (α):
α=
108 − 48
α=
3
B
1.-
o Relación de radios:
ωF − ω o
t
⇒ α = 20 rad / s
3 RP
=
18 RQ
2
⇒
RP 1
=
RQ 6
o Datos: T = 4 s
Como P y Q giran en torno a un mismo eje, sus
velocidades angulares son iguales.
problemas complementarios
ωP = ω Q
Un disco rota uniformemente alrededor de su eje,
v1 es la velocidad del punto “1” y v2 es la velocidad
del punto “2”. Los puntos “1” y “2” distan de “O” 1,5 y
2 cm respectivamente. Calcular la relación entre velocidades: v2/v1.
vP v Q
=
RP RQ
⇒
vP RP 1
=
=
v Q RQ 6
vP 1
=
vQ 6
3.-
Una partícula gira en un círculo de 3 m de diámetro a
una velocidad de 6 m/s, tres segundos después su velocidad es 9 m/s. Calcular el número de vueltas que ha
dado al cabo de 6 s.
Solución:
U|
v = 9 m / s ||
V|
t = 3s
|
a = ? (m / s ) |
W
v = 6 m/ s U
||
t=6s
|V
a = 1m/ s |
||
W
S = ? (m)
U|
S = 54 m
|V
R = 1, 5 m
|
θ = ? (rad) |W
o vo = 6 m/ s
F
Solución:
o Como se verá: Los puntos (1) y (2) giran en torno
a un mismo centro:
ω1 = ω 2 = ω
2
o
o Velocidades tangenciales:
b g
= ωb2, 0g ......... (2)
v1 = ω 1, 5 ......... (1)
v2
o (2) : (1)
2
v2 1
=
⇒
v1 3
2
2
o
v2 4
=
v1 3
o
a=
vF − v o
t
a=
9−6
3
a = 1 m / s2
1
S = v ot + at2
2
1
S=6 6 + 1 6
2
2
b g b gb g
S = 54 m
S = θR
b g
54 = θ 1, 5
θ = 36 rad
Jorge Mendoza Dueñas
154
o Finalmente:
b g
o ω = 2πf = 2π 200
2π rad
36 rad
1 vuelta
x
ω = 400 π rad / s
4.-
e = vt
o Con el proyectil:
x = 5,73 vueltas
2 = vt ........... (1)
Un ventilador gira con velocidad correspondiente a
una frecuencia de 900 R.P.M. al desconectarlo, su movimiento pasa a ser uniformemente retardado hasta
que se detiene por completo después de dar 75 vueltas. ¿Cuánto tiempo transcurre desde el momento en
que se desconecta el ventilador hasta que se detiene
por completo?
Ahora para que el proyectil penetre un sólo agujero, el cascarón deberá dar media vuelta.
Luego:
t=
Solución:
T
; siendo: T = período de revolución
2
o En (1):
o Dato:
rev 1 min
rev
×
= 15
fo = 900
min 60 s
s
fF = 0
o Aplicando: ω = 2πf
U|
ω =0
||
V|
t=?
|
# de vueltas = 75 |
W
ω o = 30 π rad / s
F
6.2π rad
1 vuelta
θ=?
75 vueltas
θ = 150 π rad
2= v
1
T
; pero: T =
f
2
2=v
FG 1 IJ
H 2 × 200 K
⇒
v = 800 m / s
Tres ruedas A, B y C, se encuentran en contacto tal
como muestra el gráfico. Siendo la velocidad angular
de “B” 200 rad/s. Hallar la velocidad angular de “A” y “C”
en rad/s si los radios son iguales a 20, 10 y 15 cm respectivamente.
o Luego:
θ=
FG ω
H
F + ωo
150 π =
5.-
2
IJ t
K
FG 30π + 0 IJ t
H 2 K
⇒ t = 10 s
Se tiene un cascarón esférico que gira con velocidad
angular constante a razón de 200 rev/s respecto a un
eje vertical. Se dispara un proyectil horizontalmente
de tal modo que pasa por el centro del cascarón. Determinar la velocidad angular del cascarón sabiendo
que su radio es igual a 1 m. Determinar también la
máxima velocidad del proyectil de tal modo que atraviesa el cascarón haciendo un solo agujero.
Solución:
o v A = vB = v C
ω ARA = ω BRB = ω CRC
b g
b g
o ω A 20 = 200 10
ω A = 100 rad / s
Solución:
o ω BRB = ω CRC
b200gb10g = ω b15g
c
ω c = 133, 33 rad / s
7.-
La rueda “A” presenta una velocidad angular constante de 40 rad/s. ¿Cuál es el valor de la velocidad angular
de la rueda “D”?
Cinemática
155
Solución:
o v A = vB
o Analizando el movimiento de rotación del
disco.
Para que el móvil regrese al mismo hueco, el tiempo de rotación de dicho hueco, debe ser también
2,4 s.
ω ARA = ω BRB
b40gb3rg = ω b2rg
⇒ ωB = 60 rad / s
B
o ω B = ω C = 60 rad / s
vC
= 60
rC
vC
= 60 ⇒ v C = 60r
r
o v C = vD
60r = ωDRD
b g
60r = ω D 5r
8.-
⇒ ω D = 12 rad / s
o Se tiene:
Un disco gira en un plano horizontal, si tiene un hueco a cierta distancia del centro por donde pasa un
móvil que luego al caer pasa por el mismo hueco. ¿Cuál
es la velocidad angular del disco en (rad/s)? (considere: g = 10 m/s2).
9.-
ω=
θ
t
ω=
π
2, 4
θ = 180° = π rad
⇒
ω = 1, 31 rad / s
Una bolita está pegada sobre un disco liso de radio “R”,
a una distancia 0,6R de su eje de giro. Si el disco está
girando a 8 rev/min y bruscamente se despega la bolita. ¿Después de cuanto tiempo saldrá despedida del
disco?
Solución:
Solución:
o Analizando el movimiento parabólico (verticalmente)
v F = v o − gt (cuando el móvil sube)
0 = 12 − 10t
⇒
b g
Ttotal = 2t = 2 1, 2
t = 1, 2 s
⇒ Ttotal = 2, 4 s
o f =8
rev min
×
min 60 s
o ω = 2πf = 2π
FG 2 IJ
H 15 K
2
rev / s
15
⇒
f=
⇒
ω=
4π
rad / s
15
Jorge Mendoza Dueñas
156
o Calculando la velocidad de la bolita.
o Se tiene:
ω o = 0 ; ω F = 80 π rad / s ; t = 5 s
v = ωr
v=
4π
0 , 6R
15
b g
⇒
v=
o Calculando la aceleración angular (α)
4
πR ........... (1)
25
ω F = ω o + αt
o En el triángulo ACB:
x=
bg
80 π = 0 + α 5
8
R ........... (2)
10
x = vt ................ (3)
o (1) y (2) en (3):
5
s
π
ωo = 0
t = 2s
;
α = 16 π rad / s2
2
⇒
θ2 = 32π rad
o Calculando el ángulo θ recorrido hasta los 3 segundos
θ 3 = ?(rad)
;
ωo = 0
t = 3s
;
α = 16 π rad / s2
θ3 = 0 × 3 +
1
16 π 3
2
b gb g
2
⇒
θ3 = 72π rad
o El ángulo recorrido en el 3° segundo será:
Solución:
fF = 2 400
;
b gb g b gb g
Las paletas de un ventilador que parte del reposo durante 5 segundos giran experimentando cambios de
rapidez a razón constante alcanzando así una frecuencia de 2 400 R.P.M. ¿Cuántas vueltas realizó durante el
tercer segundo de su rotación?
o
θ 2 = ? (rad)
1
θ = ω ot + αt 2
2
1
θ2 = 0 2 + 16 π 2
2
8
4
R = πRt
10
25
10.-
α = 16 π rad / s2
o Calculando el ángulo θ recorrido hasta los 2 segundos
o Finalmente:
t=
⇒
θ = θ3 − θ2
rev
rev 1 min
= 2 400
×
min
min
60
⇒
θ = 40 π rad
o El número de vueltas en el 3° segundo:
fF = 40 rev / s
# de vueltas =
b g
o ω F = 2πfF = 2π 40
40 π rad
= 20
2π rad
# de vueltas = 20
ω F = 80 π rad / s
PROBLEMAS PROPUESTOS
A
1.-
problemas de aplicación
Un cuerpo que posee M.C.U. gira a razón de 10 rad/s.
Si el móvil recorre 20 m en 5 s. Calcular el radio de giro.
Rpta.
3.-
A las doce del día, las agujas de un reloj están superpuestas ¿Al cabo de cuántos minutos, el minutero y el
horario formarán un ángulo de 30° por primera vez?
0,4 m
Rpta.
2.-
Un disco A gira razón de 120 R.P.M. y un punto P se
encuentra a 30 cm del centro de rotación. Otro disco
B gira A razón de 90 R.P.M y un punto Q se encuentra a
40 cm del centro de rotación. ¿Cuál de los puntos (P o
Q) tiene mayor velocidad lineal?
Rpta.
Tienen igual velocidad lineal = 120 cm/s
4.-
5,45 minutos
Los puntos periféricos de un disco que gira uniformemente, se mueven a 40 cm/s. Si los puntos que se encuentran a 2 cm de la periféria giran a 30 cm/s. ¿Qué
diámetro tiene el disco?
Rpta.
16 cm
Cinemática
5.-
157
En la figura, si la rueda mayor gira a razón de 3 rad/s.
Calcular la velocidad angular de la rueda menor.
B
1.-
Rpta.
6.-
9 rad/s
Si la aceleración tangencial de “A” es 3 m/s2. calcular la
aceleración angular de “C” en rad/s2.
(RA = 2 cm, RB = 8 cm, RC = 6 cm).
Rpta.
8.-
9.-
3.-
α = −10π rad/s2 ; n = 50 vueltas
Hallar la velocidad lineal con que giran los puntos de
la superficie terrestre que se encuentra a latitud
60° Norte (radio de la Tierra = 6 370 km).
Rpta.
10.-
60π rad
Rpta.
4.-
1 668 km/h
3 vueltas
Los radios de las ruedas de la bicicleta que se mueve en
la trayectoria circular mostrada en la figura, están en la
relación de 5 a 1, determinar en qué relación estarán el
número de vueltas que dió cada
llanta, si se sabe
que el ciclista dió
la vuelta completa
a la pista en 120 s
y R = (20/π ) m.
Rpta.
5.-
198
Un cuerpo que parte del reposo posee una aceleración
angular constante y tarda 2 minutos en recorrer entre
2 puntos de la trayectoria circular un desplazamiento
angular de 24 revoluciones. Si cuando pasa por el segundo punto gira a 18 R.P.M. Hallar el número de revoluciones entre el primer punto y el punto de partida.
Rpta.
834 km/h
¿Con qué velocidad deberá volar un avión en el Ecuador, de Este a Oeste, para que sus pasajeros les parezca que el sol está fijo en el firmamento?
(radio de la Tierra = 6 370 km).
Un tocadisco gira a 33 R.P.M. Al cortar la corriente la
fricción hace que el tocadisco se frene con desaceleración constante, observándose que luego de 3 s
gira a 32,5 R.P.M. ¿Qué tiempo en segundos, tarda el
tocadisco para detenerse?
Rpta.
La velocidad angular de un motor que gira a 1 800 R.P.M.,
en 2 segundos desciende uniformemente hasta
1 200 R.P.M. ¿Cuál es la aceleración angular? Y ¿Cuántas
vueltas dió el motor en dicho tiempo?.
Rpta.
150 rad/s
0,5 rad/s2
Una rueda gira con velocidad de 2 rev/s y se detiene
en 0,5 minutos. Si la desaceleración es uniforme, calcular el ángulo descrito.
Rpta.
La figura nos indica dos poleas coaxiales, fijas entre
ellas, de radio r1 = 0,3 m y r2 = 0,2 m y una tercera
polea de radio r = 0,4 m. El cuerpo F desciende con
aceleración constante a = 8 m/s2 partiendo del reposo. Calcule la velocidad angular de la polea de radio r
en un instante t = 5 s. Si se sabe que no hay deslizamiento entre las poleas.
Rpta.
2.-
7.-
problemas complementarios
5a1
En el sistema de transmisión de la figura: rA = 0,3 m;
rB = 0,5 m y rC = 0,2 m. Si la rueda A acelera a razón de
10 rad/s2, ¿Qué velocidad adquirirá el
bloque P a los 15 s de
iniciado su movimiento? (en m/s).
Rpta.
18 m/s
Jorge Mendoza Dueñas
158
6.-
A 4,9 m de altura sobre un punto “P” marcado en la periferia de un disco de 45 R.P.M. se deja caer una piedra
en el preciso instante en que el disco empieza a girar
(ω = cte). Al caer dicha piedra sobre el disco. ¿A qué distancia del punto “P” lo hará? Radio del disco = 15 cm
(g = 9,8 m/s2).
Rpta.
7.-
15 2 cm
Si consideramos que el radio de la Tierra es de 6 360 km
y que ella tarda 24 h en dar una vuelta. Calcular la velocidad lineal de un punto del Ecuador.
Rpta.
530π km / h
Determinar con qué velocidad tangencial giran los
puntos sobre la superficie terrestre ubicados a 45° de
latitud y sobre el nivel del mar.
(R = radio de la tierra = 6 400 km).
Rpta.
8.-
9.-
800 π
km / h
3
Un cilindro gira a 5 rad/s; un proyectil lo atraviesa con
una velocidad inicial de 340 m/s y una velocidad final
de 300 m/s. Determinar el ángulo que forma entre sí
las perforaciones y el eje del cilindro.
10.-
Se tiene una barra horizontal en reposo cuya longitud es
de 80 3 cm sostenida por dos cuerdas unidas a 2 poleas que empiezan a girar, logran hacer que la barra suba;
si las poleas giran con
velocidad angular de
120/π R.P.M. ¿Al cabo
de cuánto tiempo la
barra formará un ángulo de 60° con la horizontal? (r1 = 10 cm ;
r2 = 30 cm).
Rpta.
Rpta.
0,25 rad
1,5 s