sistemas por unidad - Cátedras Facultad de Ciencias Exactas y
Anuncio

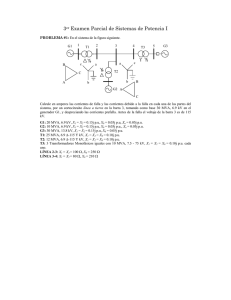
S IS T EM A P O R UNIVERSIDAD NACIONAL DE TUCUMAN Facultad de Ciencias Exactas y Tecnología Departamento de Electricidad, Electrónica y Computación 1 U N ID A D Av. Independencia 1800 – (4000) – Tucumán – Argentina Tel. +54 381 4364093 int. 7792 SISTEMAS POR UNIDAD Mag. Ing. Jorge A. González Cátedra: Sistemas Eléctricos de Potencia-Centrales Eléctricas-Energías Renovables 4 3 j0,12 pu 1 j0,1375pu j0,12 pu 2 j0,10 pu j0,0597 pu j3,345 0,669 pu 0,635 0 pu j0,0398 j0,090 pu pu j0,142 pu -4 5 6 2015 SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN 0,635 pu S IS T EM A P O R U N ID A D INDICE 1.- INTRODUCCION 2.- DEFINICION 3.- REGLAS A SEGUIR 4.- BASES MONOFASICAS y TRIFASICAS 5.- CAMBIOS DE BASE 6.- EJEMPLOS 7.- CONCLUSION SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN 2 3 S IS T EM A P O R U N ID A D SISTEMAS POR UNIDAD 1.- INTRODUCCION El valor numérico de los parámetros eléctricos (tensiones, potencias, impedancias, corrientes) para un análisis de un Sistema Eléctrico de Potencia, está generalmente expresado en un valor relativo, ya sea en por ciento [%] o en por unidad [pu]. Esto resulta como consecuencia de referenciar los valores absolutos de dichos parámetros (dados en kV, MW, Ω, kA) a sus correspondientes valores bases. Si se especifica por ejemplo una tensión base de 132 KV, entonces una tensión medida de 135,6 KV en una estación transformadora, puede quedar expresada como: 135,6 KV/132 KV = 1,027 pu ≡ 102,7 % Esta forma relativa de expresar los valores numéricos presenta las siguientes ventajas: a) Brinda información de magnitud relativa, comparando mejor las máquinas, los elementos de diferentes valores nominales y los parámetros eléctricos (una pérdida de 1MW en una línea de transmisión no tiene mayor sentido si no se menciona la potencia activa que circula por dicha línea). b) El circuito equivalente de un Trafo puede ser simplificado, desapareciendo la relación de transformación en la representación del mismo. Las impedancias, tensiones, corrientes, expresadas en [pu] no cambian cuando se refieren a un lado del Trafo o al otro. c) Las impedancias en [pu] de equipos eléctricos similares se encuentran en una estrecha faja de valores cuando los valores nominales de estos equipos son usados como valores Bases (se pueden detectar entonces errores groseros). 2.- DEFINICION Formalizando lo expresado en el punto anterior, el valor relativo en [pu] se encuentra como: Valor en [pu]α = Valor Medido [unidad correspondiente] α Valor Base Elegido [unidad correspondiente] (1) 00 El Valor Base Elegido es siempre un valor real (ángulo de 0º), por lo que el ángulo resultante α del Valor en [pu] es el mismo que el del Valor Medido. 3.- REGLAS A SEGUIR Para comenzar el proceso de transformar todo en [pu], se deben elegir arbitrariamente dos valores Bases independientes en cualquier punto del SEP. Usualmente se especifican : Una Potencia Aparente Base SB generalmente en [MVA], válida para todo el SEP analizado. Una Tensión Base UBk generalmente en [KV], para la región k correspondiente a un lado del Transformador. A partir de estos dos valores Bases se encuentra el resto de los valores Bases del Sistema, considerando que la Tensión Base de un lado k del Transformador se traslada al otro lado m del Transformador según la relación de transformación del mismo. Esto puede expresarse como: UBk UTrafo del lado k = UBm UTrafo del lado m ==> U Bm = UTrafo del lado m U Bk UTrafo del lado k SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN (2) 4 S IS T EM A P O R U N ID A D 4.- BASES MONOFASICAS y TRIFASICAS Los Valores Bases pueden ser encontrados sobre una Base por fase o una Base trifásica. Sobre una Base Monofásica Los circuitos monofásicos se resuelven usando las Bases monofásicas. Los circuitos trifásicos balanceados pueden ser resueltos también en [pu] sobre Bases monofásicas, después de convertir, si existieran, cargas conectadas en triángulo en cargas equivalentes conectadas en estrella. Valores Bases elegidos: SB 1Φ [MVA] = potencia base monofásica UB 1Φ [KV] = tensión base monofásica A partir de estas Bases se pueden deducir los otros valores bases : PB 1Φ = QB 1Φ = SB 1Φ IB = [MVA] (3) SB1Φ [KA] UB1Φ RB = XB = ZB = YB = (4) U 2 B1Φ UB1Φ = SB1Φ IB [ Ω] (5) 1 [υ] ZB (6) Sobre una Base Trifásica: Los SEP están constituidos de elementos trifásicos, y en general las potencias se expresan en potencias trifásicas, y las tensiones en valores de línea. Los circuitos trifásicos pueden ser resueltos en [pu] sobre Bases trifásicas. Valores Bases elegidos: SB 3Φ [MVA] = potencia base trifásica UBLínea [KV] = tensión base de línea A partir de estas Bases se pueden deducir los otros valores bases: PB 3Φ = QB 3Φ = SB 3Φ IB = (7) SB3Φ [KA] 3 UBLínea RB = XB = ZB = YB = [MVA] U 2 BLínea SB3Φ (8) [ Ω] (9) 1 [υ] ZB (10) SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN S IS T EM A P O R U N ID A D 5 Se relacionan los valores de base monofásicos y trifásicos: SB 1Φ = UB 1Φ = IB = 1 SB 3Φ 3 1 UBLínea 3 SB1Φ = UB1Φ ZB = [MVA] (11) [KV] (12) SB3Φ [KA] 3 UBLínea (13) U 2 B1Φ U 2 BLínea = SB1Φ SB3Φ [ Ω] (14) Los valores base monofásicos y trifásicos de corriente y de impedancia son iguales. Dado un circuito trifásico balanceado, los valores en [pu] de las tensiones, considerando base monofásica, resultan: U α [pu] = 1φ U α Medida[kV] 1φ 0 U 0Base 1φ [kV] Si ahora se trabaja con bases trifásicas, los valores en [pu] de las tensiones, considerando base trifásica, resultan: α+ 30 0 0 α + 30 Medida[kV] 3U Medida[kV] 0 U línea 1φ α + 30 U 3φ [pu] = = 00 0o U Base [kV] 3 U [kV] 1ínea Base 1φ α +30 0 │ [pu] │ U α │ [pu] = │ U 3 φ 1φ Se observa que los valores absolutos de las tensiones en [pu] son iguales numéricamente tanto si se considera la base monofásica o la trifásica de tensión en el tramo estudiado, existiendo un atraso de 300 en las tensiones en [pu] cuando se usan las bases monofásicas. De forma similar se puede demostrar que los valores de potencia en [pu] son iguales considerando tanto la base monofásica como la trifásica de potencia. SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN 6 S IS T EM A P O R U N ID A D 5.- CAMBIOS DE BASE Cuando se considera un elemento del SEP, tal como un Generador o un Transformador, los valores nominales de potencia y tensión (Sn, Un) de dicho elemento son generalmente seleccionados como los valores bases. Al analizar un elemento que está conectado al SEP, los valores bases del sistema donde se encuentra conectado el elemento (Sbase, Ubase) pueden ser diferentes de los valores de placa de ese elemento en particular(Sn, Un). Entonces es necesario ajustar los valores en [pu] de cada elemento (Xg, Xtrafo) que se habían obtenido con los valores bases de ese elemento, en los valores en [pu] de ese elemento puesto en un sistema y referidos ahora a las bases del sistema. Para encontrar los valores de impedancia en [pu] en la nueva base del sistema y en función de los valores de impedancia dados en placa, se aplica la definición (1): Zelemento SISTEMA [pu]= Zelemento[Ω] Zelemento PLACA [pu]xZB − elemento PLACA [Ω] = ZBSISTEMA [Ω] ZBSISTEMA [Ω] (15) 2 UB − elemento PLACA [KV] SBSISTEMA [MVA] Zelemento SISTEMA [pu] = Zelemento PLACA [pu] UB SISTEMA [KV] SB − elemento PLACA [MVA] (16) donde: Zelemento SISTEMA [pu] = impedancia del elemento en [pu], referenciada a la Base de la región del Sistema Zelemento[Ω] = impedancia medida del elemento, en [Ω] ZB SISTEMA [Ω] = impedancia Base de la región del Sistema donde se encuentra el elemento, en [Ω] Zelemento PLACA [pu] = impedancia del elemento en [pu], referenciado a su propia impedancia Base ZB − elemento PLACA [Ω] = impedancia Base del elemento, en [Ω] UB − elemento PLACA [KV ] = Tensión Base del elemento (dato de placa), en [KV] SB − elemento PLACA [MVA] = Potencia Base del elemento (dato de placa), en [MVA] UBSISTEMA [KV ] = Tensión Base de la región del Sistema donde se encuentra el elemento, en [KV] SBSISTEMA [MVA] = Potencia Base del Sistema, en [MVA] Nota: La expresión (16) corrige el valor en [pu] del elemento analizado, considerando las diferentes bases de potencia y de tensión que tiene el elemento cuando trabaja en forma aislada y cuando trabaja como parte de un sistema. SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN S IS T EM A P O R U N ID A D 7 6.- EJEMPLOS Ejemplo 1: Un generador entrega potencia a través de una línea de transmisión a una carga conectada en estrella. El sistema está equilibrado. Encontrar todos los valores de las variables involucradas en [pu], considerando bases monofásicas y trifásicas. G enerador Línea Dem anda Pg +jQ g Ug a Z LT a Ia ZD ZD Ug b Z LT b Ug c Z LT c Datos: b a ZD c Ug c S nominal Generador = 2 MVA U g ab U nominal Generador = Ug ab = 13,2 [kV] 30º Ug b Z fase a = 8,68+ j 3,162 [Ω] Ug a Ia ZDa = 70 + j 10 [Ω] Usando bases monofásicas: SB 1φ = 2/3 [MVA] UB 1φ = 13,8/ 3 [KV] IB = SB1Φ 2 3 = = 0,084 [KA] UB1Φ 3x13,8 RB = XB = ZB = U 2 B1Φ = 95,22 [Ω] SB1Φ SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN -U g b S IS T EM A P O R U N ID A D Los valores en [pu] de las impedancias según las bases monofásicas son: R fase [pu] = Rfase[Ω] = 0,0912 [pu] Z B [ Ω] X fase [pu] = Xfase[Ω] = 0,0332 [pu] Z B [Ω] Z LT a = 0,0912 + j 0,0332 [pu]= 0,0970 21º [pu] R demanda [pu] = Rd[Ω] = 0,7351 [pu] Z B [Ω] X demanda [pu] = Xd[Ω] = 0,1050 [pu] Z B [ Ω] ZDa = 0,7351 + j 0,1050 [pu]= 0,742 8º [pu] El diagrama de impedancias en [pu] con referencias monofásicas es: Uga ZLT a Ia ZD a La tensión de fase en [pu] en base monofásica es: Ug a [pu] = Ug a−30 º = U B1φ 13,2 −30 º = 0,957 [pu] 3x13,8 / 3 La corriente Ia en [pu] es: Ia [pu] = 0,957 −30º -39º a = = 1,142 9º + Z Da 0,838 Ug Z LTa El valor de la corriente de fase en [kA] vale: Ia = Ia [pu] * IB [kA] = 0,0955 -39º [kA] SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN 8 S IS T EM A P O R U N ID A D Usando bases trifásicas: SB 3Φ = 2 [MVA] IB = UBLínea = 13,8 [KV] SB3Φ 2 = = 0,084 [KA] 3 UBLínea 13,8 3 RB = XB = ZB = U 2 BLínea 13,82 = = 95,22 [Ω] SB3Φ 2 Los valores en [pu] de las impedancias según las bases trifásicas son: R fase [pu] = Rfase[Ω] = 0,0912 [pu] Zbase[Ω] X fase [pu] = Xfase[Ω] = 0,0332 [pu] Zbase[Ω] Z LT a = 0,0912 + j 0,0332 [pu] R demanda [pu] = Rd[Ω] = 0,7351 [pu] Zbase[Ω] X demanda [pu] = Xd[Ω] = 0,1050 [pu] Zbase[Ω] ZDa = 0,7351 + j 0,1050 [pu] La tensión nominal del generador es la tensión de línea, y su valor en [pu] en base trifásica es: Ug ab 3Φ [pu] = 13,2 Ugab = = 0,957 [pu] 13,8 U B3φ El diagrama de impedancia en [pu] es: Ug ab Z LT a Ia ZD a La corriente Ia en [pu] es: Ug Ia [pu] = 0,9570º -9º ab = = 1,142 Z LTa + Z Da 0,8389 º El valor de la corriente en [kA] por la fase a vale: Ia = Ia [pu] * IB [kA] = 0,0955 [kA] SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN 9 10 S IS T EM A P O R U N ID A D Ejemplo 2: Dado el diagrama unifilar del SEP representado en la Figura 1, encontrar su diagrama de impedancia de secuencia directa en [pu]: ZO NA 1 ZO NA 2 ZO NA 3 4 3 T34 D4 M 1 G1 2 T12 LT23 Zn34 R1 5 6 T56 D6 Zn12 R6 LT35 G6 Zn56 ZO NA 2 ZONA 4 Figura 1 Los Datos de placa de los elementos del SEP son los siguientes: Generadores y Motores Sn Un [MVA] [KV] G1 12 8 G6 15 7 D4 15 7 Transformadores Sn Upri [MVA] [kV] T 12 (DY) 15 8 T 34 (YD) 15 7 T 56 (YD) 20 7 Xd” [%] 11 13 12 Usec [kV] 132 132 138 uk [%] 10 12 11 Xi [%] 11 14 16 Xo [%] 5 6 5 Rneutro [Ω] 1000 1500 Zn alta [Ω] 10 ∞ 20 Líneas Línea 23 Línea 35 Un [kV] 132 132 Xd = Xi [Ω/km ] 0,46218 0,46218 Xo [Ω/km] 1,33000 1,33000 longitud [km] 150 100 Demanda D6 Zcarga [ Ω] 10+j2 SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN S IS T EM A P O R U N ID A D 11 Pasos en la Construcción del Diagrama de Impedancia a) Se identifican las diferentes zonas del circuito (Figura 1), dadas por los diferentes lados de los transformadores (lado de alta y lado de baja). Zona 1: El generador G1 y el arrollamiento de baja del T12. Zona 2 : El arrollamiento de alta del transformador T12, T34 y T56, la línea de transmisión LT23 y LT35. Zona 3 : El Motor M o demanda D4 y el arrollamiento de baja del T34. Zona 4 : El generador G6, la demanda D6 y el arrollamiento de baja del T56. b) Se eligen los dos valores bases trifásicos independientes (se podría haber elegido también valores bases por fase). Si bien los valores bases pueden ser cualquiera, es recomendable que el valor base de la potencia sea del orden de la potencia que maneja el sistema, y que la tensión base de la región sea la del lado del transformador correspondiente. SB 3Φ = 15 [MVA] (es el mismo para todo el SEP) UB (zona1) = 8 [KV] c) Se encuentran las tensiones bases para el resto de las zonas aplicando la expresión (2): UB (zona m) = UB (zona k) UTrafo (zona m) UTrafo (zona k) UB (zona 2) = UB (zona 1) UTrafo12 (zona 2) 132 = 8 = 132 [KV] UTrafo12 (zona 1) 8 UB (zona 3) = UB (zona 2) UTrafo34 (zona 3) 7 = 7 [KV] = 132 UTrafo34 (zona 2) 132 UB (zona 4) = UB (zona 2) UTrafo56 (zona 4) 7 = 132 = 6,696 [KV] UTrafo56 (zona 2) 138 d) Se encuentran las corrientes bases en todas las zonas aplicando la expresión (4): IB (zona k) [KA] = SB3Φ [MVA] 3 UB (zona k) [KV] IB (zona 1) = SB3Φ = 3 UB (zona 1) IB (zona 2) = SB3Φ = 3 UB (zona 2) SB3Φ = 3 UB (zona 3) SB3Φ IB (zona 4) = = 3 UB (zona 4) IB (zona 3) = 15 = 1,083 [KA] 38 15 = 0,066 [KA] 3 132 15 = 1,237 [KA] 3 7 15 = 1,293 [KA] 3 6,696 SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN S IS T EM A P O R U N ID A D 12 e) Se encuentran las impedancias bases en todas las zonas aplicando la expresión (5): ZB (zona k) [Ω] = U 2 B (zona k) SB3Φ U 2 B (zona 1) 82 = 4,266 [Ω] = SB3Φ 15 U 2 B (zona 2) 132 2 ZB (zona 2) = = = 1161,6 [Ω] SB3Φ 15 U 2 B (zona 3) 72 ZB (zona 3) = = = 3,266 [Ω] SB3Φ 15 ZB (zona 1) = ZB (zona 4) = U 2 B (zona 4) SB3Φ = 6,692 = 2,989 [Ω] 15 f) Se construye una Tabla con todos los valores Bases obtenidos de las diferentes Zonas: ZONA 1 ZONA 2 ZONA 3 ZONA 4 UB [KV] 8 132 7 6,696 IB [KA] 1,083 0,066 1,237 1,293 Tabla 1 ZB [Ω] SB [MVA] 4,266 15 1161,6 3,267 2,989 g) Se calculan las impedancias de todos los elementos en [pu], realizando los cambios de base correspondientes (expresión (14)). Generador G1: 2 2 UB − G1PLACA [KV] SBSISTEMA [MVA] 8 15 ZG1SISTEMA = ZG1 PLACA [pu] = 0.11 = 0,1375 [pu] 8 12 UB ZONA 1 [KV] SB − G1PLACA [MVA] Generador G6: 2 2 UB − G 6 PLACA [KV] SB SISTEMA [MVA] 7 15 ZG 6 SISTEMA = ZG 6 PLACA [pu] =0,13 =0,1421 [pu] 6,696 15 UB ZONA 4 [KV] SB − G 6 PLACA [MVA ] Motor M4: 2 2 UB − M 4 PLACA [KV] SB SISTEMA [MVA ] 7 15 = 0.12 = 0,12 [pu] ZM 4 SISTEMA = ZM 4 PLACA [pu] 7 15 UB ZONA 3 [KV] SB − M 4 PLACA [MVA] no cambia de valor, ya que las bases del elemento son las mismas que las del sistema. Transformador 12: 2 2 UB − T12 PLACA [KV] SB SISTEMA [MVA] 8 15 = 0,10 = 0,10 [pu] ZT12 SISTEMA = ZT12 PLACA [pu] 8 15 UB ZONA 1 [KV] SB − T12 PLACA [MVA] SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN S IS T EM A P O R U N ID A D Transformador 34: 2 7 15 = 0,12 [pu] ZT 34 SISTEMA = 0,12 7 15 Transformador 56: 2 7 15 = 0,090 [pu] ZT 56 SISTEMA = 0,11 6,69 20 Línea de Transmisión 23 XLT [Ω] = XLT [Ω/km] x longitud [km] XLT [Ω] ZB (zona k) XLT [pu] = XLT23 = 0,46218 x 150 = 69,3 [Ω] XLT23 = 69,3 = 0,0597 [pu] 1161,6 Línea de Transmisión 35 XLT35 = 0,46218 x 100 = 46,218 [Ω] XLT35 = 46,218 = 0,0398 [pu] 1161,6 Demanda 6 ZD6 [pu] = ZD6 = ZD6 [Ω] ZB (zona 4) [Ω] 10+ j2 = 3,346 + j0,669 [pu] 2,989 SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN 13 S IS T EM A P O R U N ID A D 14 h) Se calculan las Tensiones de los Generadores en [pu] Se supone que la tensión del generador 1 detrás de su reactancia directa es un 10 % superior a su tensión nominal y posee un ángulo de 0º: EG1 = 8,8 1,1xUG1 [KV] = = 1,1 0º [pu] UB (zona 1) [KV] 8 Se supone que la tensión del generador 6 detrás de su reactancia directa es un 5 % superior a su tensión nominal y posee un ángulo de -4 º : EG6 = 7,35 1,05xUG6 [KV] = = 1,098 -4º [pu] 6,696 UB (zona 4) [KV] h) Con los valores encontrados en [pu] se construye el diagrama de impedancias de secuencia directa mostrado en la Figura 2: 4 3 j0,12 pu j0,12 pu 1 j0,1375 pu 2 j0,10 pu j0,0597 pu 3,346 1,1 0 j0,669 pu pu j0,0398 j0,090 pu pu j0,142 pu -4 5 6 1,098 pu Figura 2 Se observa que el diagrama obtenido es un circuito eléctrico sin transformadores, donde se pueden aplicar los teoremas convencionales de resolución de circuitos para encontrar todas las corrientes, tensiones y potencias presentes en [pu]. Para saber cuanto valen en [KA], [KV] y [MW] se multiplican estos valores encontrados en [pu] por la base de la zona correspondiente. Por ejemplo, la corriente que circula por la carga conectada a la barra 6 tiene el siguiente valor en [KA] : ID6[KA] = ID6 [pu] x IB (zona 4) [KA] SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN S IS T EM A P O R U N ID A D 15 7.- CONCLUSION El Sistema Por Unidad es una herramienta que permite construir, a partir del diagrama unifilar y de los datos de los diferentes elementos que lo componen, un diagrama de impedancias en [pu] sin que aparezcan en forma explícita los transformadores. Aplicando los diferentes teoremas de cálculo al circuito eléctrico formado, se podrán encontrar todas las variables eléctricas involucradas en [pu] y posteriormente sus valores en [KA], [KV] y [MW]. 8.- BIBLIOGRAFIA 1.- Olle Elgered, Electric Energy Systems Theory, McGraw Hill, 1982. 2.- Duncan Glover, Mulukutla Sarma, Power System Analysis an Design, PWS Publishers, McGraw Hill, 1994. 3.- John Grainger, William Stevenson, Análisis de Sistemas de Potencia, Mc Graw Hill, 1996. SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN S IS T EM A P O R U N ID A D 16 ANEXO EL TRANSFORMADOR Y-∆ Este tipo de transformador se usa en general para vincular un generador con una línea de transmisión. El lado de baja (G) se conecta al ∆ y el de alta (LT) a la Y. Una ventaja de la Y en alta, es que posee un punto neutro para conectar a tierra, disminuyendo por lo tanto las necesidades de aislamiento de los arrollamientos, ya que se los puede ahusar desde un valor máximo en los terminales, a un mínimo en el centro de la Y. Una ventaja de la ∆ es que la corriente magnetizadora de 3ra. Armónica, causada por la característica B-H del núcleo, permanece atrapada dentro del ∆ . La figura muestra esquemáticamente un trafo Y-∆, donde el lado de Alta está en Y (subíndices en mayúsculas) y el lado de baja en ∆ (subíndices en minúsculas). Los devanados dibujados en paralelo están enlazados por el mismo flujo (por ejemplo, devanado AN con el devanado ab), y si se tiene en cuenta además la ubicación de los puntos, resulta que la tensión de fase a neutro VA de la Y, está en fase con la tensión de línea Vab del ∆ (independiente de la secuencia de fases). A partir de esto se puede construir el resto del diagrama fasorial para la componente de secuencia positiva. A a IA Ia I ab B I ca N c IB I bc Ic C b Ib IC B V ab a V AB b Va Vb A VB VA V BC V ca Vc V bc VC V CA C C SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN S IS T EM A P O R U N ID A D 17 Se puede observar que la tensión de fase VA en el lado Y (Alta) adelanta en 30º a la tensión de fase Va en el lado del ∆ (baja). Si N1 y N2 representan el número de espiras en los devanados de alta y baja respectivamente, entonces la relación entre las tensiones de fase de ambos lados es: VA = N1 N1 Vab = N2 N2 V N1 3 Va e j30 ==> A = N2 Va 3 e j30 También se puede encontrar que la relación de tensiones de líneas en ambos lados es: VAB N1 = Vab N2 3 e j30 Resultando: VA V N1 = AB = N2 Va Vab 3 e j30 De la misma manera, las corrientes del lado de alta se encuentran desfasadas 30º respecto de las del lado de baja en la misma dirección que las tensiones. El desfasamiento puede ser indicado a través de un trafo ideal que tenga una relación de espiras de 1: e j30 . Ia Vg α -30º IA Z trafo V a ϑ -30º VA ϑ 1:e α Z carga j30º Regla: Las tensiones y corrientes del lado de alta, están adelantados 30º respecto del lado de baja. SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN S IS T EM A P O R U N ID A D 18 Es importante señalar que el desfasaje introducido por el trafo, no afecta los flujos de potencia real y reactiva: ϑ I − α = V ( ϑ − 30º ) I ( − α + 30º ) S [pu] = VA a a A S [pu] = VA I A ( ϑ− α) = Va I a ( ϑ− α) Por lo tanto si se requieren las cantidades P y Q sobre un diagrama de impedancias, no es necesario considerar el desfasamiento introducido por el trafo Y-∆. El único caso en que no se puede ignorar el desfasaje es cuando el producto de las relaciones de tensión de los trafos, no es unitario alrededor de un lazo del sistema. La impedancia en pu de un trafo, es igual independiente del lado al que está referida: V VA = a = Z [pu] IA Ia Nota: Realizando el mismo análisis, se puede encontrar que cuando se alimenta con una secuencia negativa el lado en Y, la VA atrasa en 30º a la tensión Va. SISTEMAS ELECTRICOS DE POTENCIA – UNIVERSIDAD NACIONAL DE TUCUMÁN