• La fuerza es una magnitud vectorial que mide la intensidad de la

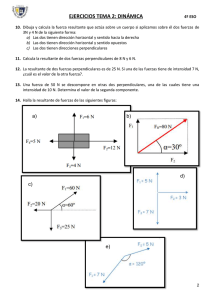
TEMA 7: FUERZAS. COMPOSICIÓN DE FUERZAS
CONCEPTO DE FUERZA
Hasta ahora hemos estudiado el movimiento de los cuerpos sin preocuparnos de la causa que lo produce. ¿Por qué se
mueven los cuerpos?, ¿por qué aceleran?, ¿por qué giran?...
El concepto de fuerza es uno de los más importantes de la física y su significado científico no coincide con su
significado cotidiano. Para verlo contesta a estas preguntas.
• ¿Qué es para ti la fuerza?
• ¿Tienen fuerza los cuerpos?
• Señala cuál de estos cuerpos tiene más fuerza: Hombre escopeta coche mesa polea libro bomba
• ¿Cómo sabes que un cuerpo tiene o no fuerza?
• Pon dos ejemplos en los que existan fuerzas.
Para que existan fuerzas es necesario que dos cuerpos interactúen. No hablaremos de la fuerza que tiene un cuerpo
sino de la fuerza que ejerce un cuerpo.
Hay varias definiciones de la fuerza:
•
La fuerza es una magnitud vectorial que mide la intensidad de la interacción entre dos cuerpos
•
Fuerza es toda acción capaz de alterar el estado de reposo o de movimiento
movimiento de un cuerpo o de producir en él
alguna deformación
La fuerza es una magnitud vectorial y como tal tiene:
- módulo
- dirección
- sentido
- punto de aplicación.
La unidad de la fuerza en el S.I. es el NEWTON (N
N). Para hacernos una idea su valor, diremos que una mandarina
pesa un Newton (aproximadamente el peso de unos 100 g)
Hay otras unidades para medir la fuerza como por ejemplo el KILOPONDIO (Kp
Kp)
Kp que es el peso de un cuerpo de
1 Kg de masa.
1 Kp = 9,8 N
Al ser la fuerza una magnitud vectorial, hemos de sumarlas como vectores, cosa que veremos más adelante.
Cuando sobre un cuerpo actúen varias fuerzas, las sumaremos todas y su resultado será la fuerza, FR, resultante, FR,
que ejerce el mismo efecto que todas las fuerzas juntas.
COMPOSICIÓN
COMPOSICIÓN DE FUERZAS
Sobre un cuerpo pueden actuar varias fuerzas. La fuerza resultante (R) de todas es una fuerza que produce el mismo
efecto que todas las otras actuando simultáneamente. Como las fuerzas son magnitudes vectoriales para calcular su
resultante hemos de tener en cuenta no solo el módulo, sino la dirección y el sentido.
Veamos los distintos casos para calcular la resultante.
a)
F1 = 2 N
F2 = 5 N
R=2+5=7N
b)
F1 = 1 N
F2 = 4 N
R=4–1=3N
c)
d)
e) En general cuando tenemos varias fuerzas, para calcular la resultante se colocan una detrás de la otra,
manteniendo sus direcciones, y se unen el origen con el final.
f) La resultante de dos fuerzas paralelas del mismo sentido (sentido contrario) y con diferente punto de aplicación
es una fuerza paralela a estas y con el mismo sentido. Su modulo es igual a la suma de los módulos de estas (la
resta), y su punto de aplicación esta situado entre estas y se calcula sabiendo que se cumple que:
F1 ⋅ x = F2 ⋅ (d − x )
Ejercicios.
1. Calcula numérica y gráficamente
gráficamente la resultante de las fuerzas F1 =(2 , 3) y F2 =(=(-3 , 0)
2. Halla la suma de tres fuerzas F1 ((-1,3),
1,3), F2 (5,(5,-3),
3), F3 ((-1,4) y el módulo de la resultante.
3. Sobre un cuerpo actúan las fuerzas de la
la figura. Calcula el valor de la fuerza resultante, su dirección y su
sentido
4. Hallar la fuerza resultante
resultante de dos fuerzas de 0,5 N y 1,5 N del mismo sentido aplicadas al extremo de una
barra de 5 m y su punto de aplicación.
5. Un padre soporta
soporta 3 veces más carga que su hijo. En qué punto de una barra de 1 m debe colgarse una masa
de 80 kg.
DESCOMPOSICIÓN DE FUERZAS
Es conveniente considerar una fuerza F como la suma de dos fuerzas dirigidas según los ejes de coordenadas
cartesianas: F = Fx + Fy
Las componentes Fx y Fy son:
Fx
Fy
Ejercicios.
6. Un hombre tira con una fuerza de 400 N de una cuerda atada a un coche. La cuerda forma un ángulo de 30º
con la horizontal. Calcula las componentes x e y de la fuerza.
7. Un cuerpo de 200
200 N de peso, se desliza sobre un plano inclinado 25º sobre la horizontal. Calcula las
componentes del peso.
LEY DE HOOKE
Al tirar de los extremos de un muelle ejerciendo una fuerza, produciremos en él una deformación que sera mayor
cuanto mayor sea la fuerza ejercida.
Si colgamos el muelle de un soporte y tiramos con fuerza de él, por ejemplo, colgando una pesa, el muelle de longitud
L0, se alargará hasta alcanzar una longitud L. El alargamiento será, por tanto, L – L0.
Está demostrado que si duplicamos la fuerza también duplicaremos el alargamiento, es decir, el alargamientodel
muelle es directamente proporcional a la fuerza aplicada (LEY DE HOOKE).
F = K ⋅ ∆L
F = K ⋅ (L − L0 )
Donde K es la llamada constante de elasticidad del muelle y se mide en el SI en N/m. Si decimos que la constante
de elasticidad de un muelle es de 30 N/m quiere decir que para estirar un metro la longitud del muelle necesitamos
ejercer sobre él una fuerza de 30 N.
Esta ley se cumple siempre que no deformemos el muelle.
Para medir las fuerzas se utiliza un dispositivo llamado dinamómetro. Su funcionamiento se basa en la ley de
Hooke. Se trata básicamente, de un muelle del cual se conoce su constante de elasticidad y, por tanto, se puede conocer
el alargamiento que corresponde a cada fuerza aplicada.
Ejercicio.
8. Tenemos dos muelles, uno cuya constante elástica es de 10 N/m y el otro, 14 N/m. ¿Cuál de los dos cuesta
más de comprimir?
9. Tenemos un muelle que mide normalmente 10 cm. Al tirar de él con una fuerza de 5 N, observamos que su
longitud pasa a ser de 12 cm.
a) Calcular
Calcular la constante elástica del muelle.
b) ¿Cuál será su longitud si ejercemos una fuerza de 2 N?
c) ¿Con qué fuerza debemos tirar para que pase a medir 15 cm?
EQUILIBRIO DE LOS CUERPOS
Los cambios que en el movimiento de los cuerpos producen las fuerzas pueden ser traslaciones o rotaciones. Vamos a
ocuparnos de las rotaciones.
Cuando las fuerzas que actúan sobre cuerpos que no pueden trasladarse, por tener algún punto o eje fijo, pueden
hacerlos girar. Para medir estos giros, se ha definido una nueva magnitud, el momento de una fuerza,
fuerza que relaciona
la fuerza y la distancia entre ella y el punto fijo alrededor del cual gira el cuerpo.
Momento de una fuerza, respecto a un punto, es el producto de la fuerza por la distancia del punto a la fuerza:
M=F.d
Al ser el momento una magnitud vectorial hemos de establecer un sistema de signos para indicar el sentido del vector
momento. El momento es un vector perpendicular al plano formado por d y F y su signo será positivo si el giro se
produce en el sentido de las agujas del reloj (sentido horario) y negativo si el giro es en el sentido antihorario.
La unidad del momento en el SI es el N . m.
m
Para que un cuerpo esté en equilibrio,
equilibrio es necesario que la resultante de todas las fuerzas y de todos los momentos
sean nulos.
Hay que recordar que el hecho de que un cuerpo esté en equilibrio, no implica, forzosamente, que esté en reposo
(equilibrio estático), sino que puede estar en movimiento (equilibrio dinámico)
Ejercicios
Ejercicios.
10. Si queremos abrir una puerta aplicándole una fuerza que pase por el eje de giro, ¿lo conseguiremos?
¿Por qué?
11. Si para abrir la puerta se necesita un momento de 23 N.m, ¿qué fuerza hay que ejercer a 30 m del eje
de giro?
12. Dos masas de 25 Kg y 50 Kg están colgadas de los extremos de una barra de 3 m de largo. Si apoyamos la
barra en un punto situado a un metro de la masa mayor, ¿estará en equilibrio el sistema?.
Si no lo está, ¿dónde habrá que situar el punto de apoyo para equilibrarlo?
EJERCICIOS
1.
2.
3.
4.
5.
6.
Describe algunos ejemplos en los que se pongan de manifiesto cada uno de los efectos que producen las fuerzas.
¿Cuál es la condición indispensable para que se manifieste una fuerza?
Demuestra, empleando algún ejemplo, que el efecto de la fuerza depende de la dirección y del sentido que se le aplique.
Si a un cuerpo le aplicamos dos fuerzas, una de 10 N y otra de 15 N, ¿cuánto vale la fuerza resultante?
Explica qué elementos de la fuerza ha de tener en cuenta un jugador de billar.
Halla el módulo de la resultante de dos fuerzas de 8 N y 15 N, respectivamente, que forman un ángulo de 90º.
7. Una fuerza de 15 N actúa en la misma dirección y sentido contrario que otra fuerza de 35 N. En el punto de aplicación
común de estas fuerzas y perpendicular a ellas actúa una fuerza de 25 N. determina la dirección, sentido y módulo de la
resultante.
8. Cuatro fuerzas concurrentes de 5 N, 10 N, 15 N y 20 N actúan sobre un mismo cuerpo según la dirección y sentido de los
cuatro puntos cardinales, N, S, E y O, respectivamente. Representa las fuerzas y calcula su resultante. SOL: 7,07 N
9. Tres fuerzas concurrentes pueden equilibrarse entre sí. Explica mediante un esquema qué disposición han de tener.
10. Dibuja la resultante en cada uno de estos casos:
11. Halla la resultante de estas fuerzas:
Sol: 7’81 N en diagonal y hacia
hacia abajo a la derecha.
12. Dos alumnos tiran, en direcciones perpendiculares, de dos cuerdas atadas a la pata de una mesa, uno con una fuerza de
200 N, y el otro, con una de 250 N. ¿Con qué fuerza y en qué dirección tendrá que tirar otro alumno para que la mesa no se
mueva? Haz un dibujo.
13. Suma tres fuerzas que tienen como origen el origen de coordenadas y por extremos A(5,2)N, B(2,3)N y C(-4,-6)N;
represéntalas en los mismos ejes de coordenadas.
a) Representa las tres fuerzas y el vector que representa la suma.
b) Halla el valor en Newtons del vector suma. Sol: 10 N
14. ¿Puede estar un cuerpo en equilibrio si sobre él actúa una sola fuerza?
15. Sobre un cuerpo se aplican las siguientes fuerzas: F1 = 3 N dirigida según el eje X positivo, F2 = 3 N según el eje Y
negativo. Calcula la tercera fuerza necesaria para que el sistema esté en equilibrio. Sol.: F3 = 18 N
16. Calcula el valor de las componentes rectangulares de una fuerza de 50 N que forma un ángulo de 60° con el eje horizontal.
¿Cómo sería la fuerza que habría que aplicar para que el sistema se encontrase en equilibrio?
Sol.: Fx = 25 N y Fy =43,30
=43,30 N
17. Señala lo que consideres que es cierto.
Cuando se aplican dos fuerzas de 20 N y 21 N, respectivamente, en un punto de un sólido rígido, la resultante puede ser una
fuerza de: a) 41 N. b) 1 N. c) Nula. d) 29 N.
18. Sergio y Adrián sujetan en el aire un baúl, tirando cada uno de una de las asas. Las fuerzas que ejercen son de 40 N y
60 N, respectivamente, y forman entre sí un ángulo de 90º. ¿Cuál es el peso del baúl? Sol: 72,11 N
19. La resultante de dos fuerzas que forman un ángulo de 90º es de 30 N y una de las componentes vale 12 N. ¿Cuál es el
módulo de la otra componente? Sol: 27,49 N
20. Se sabe que el módulo de la resultante de dos fuerzas perpendiculares es de 27,3 N. Si una de ellas vale 24 N, ¿cuánto vale
la otra? Sol: 13,01 N
21. Halla la intensidad, dirección, sentido y punto de aplicación de la resultante de dos fuerzas paralelas, de 40 N y 60N,,cuyas
líneas de acción distan entre sí 80 cm:
a) si las dos fuerzas son del mismo sentido.
b) si son de sentidos contrarios.
Sol: a) 100N a 0,48 m de la de 40 N b) 20 N a 0,48 m de la de 40 N
22. Un tablón homogéneo, de 250 N de peso y 2,4 m de longitud, se mantiene horizontal colgado de dos cuerdas verticales. Una
de ellas, que está atada a un extremo, hace una fuerza de 100 N. ¿Qué fuerza soporta la otra cuerda y a qué distancia del
extremo está sujeta? Sol:
Sol: 150 N a 0,4 m del extremo
23. La resultante de dos fuerzas paralelas y del mismo sentido es de 200 N. Si una de ellas es de 120 N y dista 40 cm de la
resultante, ¿cuál es la intensidad de la otra y la distancia entre ambas?. Sol: 80 N , 1 m
24. La resultante de dos fuerzas paralelas del mismo sentido dista de ellas 30 cm y 40 cm, respectivamente. ¿Cuáles serán las
intensidades de dichas fuerzas si la resultante vale 210 N? Sol: 120 N y 90 N.
25. Sobre uno de los extremos de una barra rígida de 80 cm de longitud se aplica una fuerza de 15 N, y sobre el otro extremo una
fuerza desconocida con la misma dirección y sentido que la anterior. Sabiendo que la resultante del sistema se aplica a
30 cm del extremo donde actúa la fuerza desconocida.
a) Representa el diagrama de fuerzas.
b) Halla el módulo de la segunda fuerza.
c) Calcula el módulo de la resultante y represéntala en el diagrama de fuerzas. Sol: b) 25 N c) 40 N
26. Se tienen tres fuerzas de 5 N, 8 N y 10 N que forman, respectivamente, ángulos de 30°, 45° y 60° con la horizontal, y que se
aplican sobre un mismo punto. Calcula gráfi ca y numéricamente la fuerza que provocará el equilibrio de las tres sobre el
punto de aplicación. Sol: 22,53 N
27. Dos personas transportan un cuerpo de 600 N que cuelga de una barra de 2 m de longitud. Si queremos que uno soporte
doble fuerza que el otro, ¿a qué distancia de los extremos se ha de colgar el cuerpo?
Sol: A 1, 33 m del extremo que soporta menos fuerza
28. De los extremos de una barra rígida, de dos metros de longitud, se cuelgan dos cuerpos de 50 N y 70 N, respectivamente. ¿A
qué distancia de los extremos se ha de apoyar la barra para que esté en equilibrio?
29. Se aplican a un cuerpo dos fuerzas de 10 N y 20 N formando un ángulo recto. ¿Qué fuerza habrá que ejercer y en qué
dirección y sentido para que el cuerpo no se mueva? Sol: 22,36 N.
30. Dos fuerzas de 15 y 12 N se aplican a un cuerpo formando un ángulo de 90º. ¿Qué fuerza debe aplicarse al cuerpo para que
permanezca en equilibrio? Sol: 13 N.
31. Dos chicos aplican sendas fuerzas de 30 N y 40 N hacia arriba y con un ángulo de 30° a fi n de conseguir sacar de un pozo
un saco de 50 N de peso. Indica si lo conseguirán.
32. Un muelle alcanza la longitud de 82 cm cuando se tira de él con una fuerza de 480 N, y la de 90 cm cuando se le aplica
una fuerza de 600 N. Halla el valor de la constante k, y lo que mide el muelle cuando no actúa ninguna fuerza sobre él.
33. Un muelle se alarga 2 cm por la acción de una fuerza de 300 N. Calcula:
a) El valor de la constante de recuperación. b) La fuerza que habrá que aplicarle para producir un alargamiento de 5 cm.
34. Calcula la constante de elasticidad de un muelle, sabiendo que cuando se tira de un extremo de él con una fuerza de 100 N
pasa de tener una longitud de 20 cm a otra de 25 cm.
35. Se tira de un muelle de constante K=3000 n/m con una fuerza desconocida. El muelle que media 5 cm se estira hasta
medir 62 cm. Calcula el valor de la fuerza. Sol: 360 N.
36. Para abrir una puerta hace falta aplicar una fuerza de 3 N a una distancia de 60 cm de las bisagras. Si aplicamos una
fuerza de 7 N a 10 cm de las bisagras, ¿podremos abrir la puerta?
37. ¿Dónde debe empujarse una puerta para cerrarla con mayor facilidad? ¿Por qué?
38. Las figuras siguientes representan puertas que pueden girar alrededor de un punto A, y sobre ellas actúan fuerzas que las
hacen girar. Suponiendo que las puertas son iguales: ¿Qué puerta girará más?
39. La figura representa una puerta que puede girar alrededor del punto O. Observa y contesta:
a) ¿De las tres fuerzas, cuales tienden a hacer girar la puerta en el mismo sentido?
b) ¿Qué vale el momento de cada fuerza?
c) ¿En qué sentido girará la puerta? Justificarlo.
Sol: a) F1 y F2; b) M1=4,5N.m; M2=13,5N.m; M3 = -20 N.m; c) En el sentido de las agujas del reloj.
1.
2.
3.
4.
5.
6.
7.
AUTOEVALUACIÓN
Halla gráficamente la resultante de cada uno de estos grupos de fuerzas y calcula su intensidad.
Un caballo tira de un carromato con una fuerza de 2 000 N y le ayuda el carretero con una fuerza de 250 N. Si el suelo
opone una fuerza de rozamiento de 150 N, calcula la fuerza que realmente impulsa al carromato.
Un hombre, usando una cuerda, tira de una caja de 2,5 Kg con una fuerza de 10N, mientras la cuerda forma un ángulo de
60º con la horizontal.
a) Representa todas las fuerzas que intervienen.
b) Calcula la fuerza resultante.
Calcula el valor de las componentes x e y del peso correspondiente a un cuerpo de 50 N de peso colocado sobre un plano
inclinado de 30º de inclinación.
Se cuelga un peso de medio kilogramo de un resorte y se observa que el resorte se estira 10 cm. Calcular
a) La constante elástica del resorte.
b) La fuerza que hemos de ejercer para alargarlo 35 cm.
Una barca atraviesa un río empujada por el remero con una fuerza de 350 N y por la corriente que la arrastra
perpendicularmente con otra fuerza de 100 N. ¿Cuál es la fuerza que hace avanzar la barca?
En un balancín de 4 m de largo se columpian dos niños de 20 y 30 kg en sus extremos ¿En dónde se tendría que colocar un
adulto de 70 kg para lograr el equilibrio?
8.
Se desea colgar del techo un cuerpo de 2 kg de masa mediante dos cuerdas igual de largas y que forman entre sí un ángulo
de 60 º. Calcula la tensión que soporta cada cuerda.
9. En los extremos de una barra de 2 m de longitud se ejercen dos fuerzas paralelas y de sentido contrario de 10 N y 20 N y
perpendiculares a la barra. Determina
a) el módulo de la fuerza resultante;
b) la distancia del punto de aplicación a fuerza de 10 N.
10. Dos lanchas tiran del esquiador como se muestra en la figura. Si el sistema está en equilibrio y cada lancha hace una fuerza
de 600N ¿Cuál es la fuerza neta sobre el esquiador?
11. Un alumno muy inteligente de 4° año secundaria, ata con una soga el extremo del paragolpes del coche de su familia que ha
quedado atascado en el barro, y el otro extremo a un árbol como se ve en la figura. Luego empuja del punto medio de la
cuerda, haciendo una fuerza que calcula en 300N. El automóvil comienza a moverse cuando se forma un ángulo θ =5° ¿Con
qué fuerza tira la cuerda del coche?