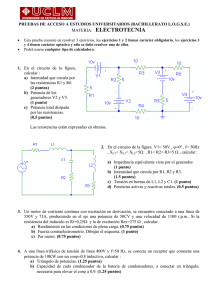
Generador sincrónico trifásico DL 1026A.

Always leading the pack
GENERADOR SINCRONICO
TRIFASICO
DL 1026A
Laboratorio Unilab
DL 1026A
Página blanca
DE LORENZO
Sistemas para la
formación técnica
II
DL 1026A
INDICE
Generalidades
Prueba Nº 1
Prueba Nº 2
Prueba Nº 3
Prueba Nº 4
Prueba Nº 5
Prueba Nº 6
Prueba Nº 7
Prueba Nº 8
Prueba Nº 9
Prueba Nº 10
Prueba Nº 11
Pag.
1
Medida de la resistencia de los
devanados.
Pag.
3
Relevación de las características de
magnetización.
Pag.
7
Medida de las pérdidas mecánicas en el
hierro.
Pérdidas adicionales.
Pag.
11
Relevación de las características de
cortocircuito permanentes trifásicas.
Pag.
17
Diseño de la curva de impedencia
sincrónica.
Método de Behn-Eschemburg.
Pag.
21
Características de regulación con el
método indirecto de Behn-Eschemburg.
Pag.
25
Características externas con el método
indirecto di Behn-Eschemburg.
Pag.
31
Relevación de un punto de la
característica a carga swattado.
Determinación de los coeficientes Xd y α
según Potier.
Pag.
35
Características de regulación con el
método indirecto de Potier.
Pag.
41
Características externas con el método
indirecto de Potier.
Pag.
47
Relevación directa de algunas
características exteriores.
Pag.
49
DE LORENZO
Sistemas para la
formación técnica
III
DL 1026A
Prueba Nº 12
Relevación directa de algunas
características de regulación.
Pag.
51
Prueba Nº 13
Rendimiento convencional del alternador
Pag.
53
Prueba Nº 14
Paralelo del alternador con la red.
Regulación del intercambio de P y Q.
Pag.
59
Curva a "V" o de Mordey del motor
síncrónico.
Pag.
63
Pag.
69
a) Medida de la resistencia de los
devanados de inducido
b ) Medida de la resistencia de
excitación.
Pag.
71
Pag.
73
Relevación de las características
de magnetización.
Pag.
75
Medida de las pérdidas mecánicas
en el hierro y adicionales.
Pag.
77
Relevación de las características
de cortocircuito.
Pag.
81
Relevación de las características
exteriores.
Pag.
83
Relevación de las características
de regulación.
Pag.
87
Paralelo del alternador con la red
trifásica.
Pag.
89
Relevación de una curva a "V".
Pag.
93
Prueba Nº 15
EJERCICIOS PRACTICOS
Datos de placa
Prueba práctica Nº 1
Prueba práctica Nº 2
Prueba práctica Nº 3
Prueba práctica Nº 4
Prueba práctica Nº 5
Prueba práctica Nº 6
Prueba práctica Nº 7
Prueba práctica Nº 8
DE LORENZO
Sistemas para la
formación técnica
IV
DL 1026A
GENERALIDADES
Los datos nominales de la máquina en prueba, normalmente los suministra el fabricante, se
aplican en una placa y sirven como "tarjeta de identidad" de modo que el usuario pueda
individuar las características de funcionamiento mas importantes.
Dado que estos valores nominales son el resultado de pruebas que el fabricante ha efectuado
en elgunos prototipos, al inicio de la producción en serie, cada máquina producida podrá
variar un poco de los datos standard esto como causa de las distintas tolerancias
constructivas.
La prueba de una máquina en serie consiste en controlar si se respetan las prestaciones
reportadas en la placa y relevar las características de funcionamiento que aunque no
aparacen en la placa son de interés en el uso que se le da a la máquina.
DE LORENZO
Sistemas para la
formación técnica
1
DL 1026A
Página blanca
DE LORENZO
Sistemas para la
formación técnica
2
DL 1026A
PRUEBA
Nº 1
MEDIDA DE LA RESISTENCIA DE LOS DEVANADOS
El valor de la resistencia de los devanados del alternador es útil para poder determinar lo
siguiente:
- rendimiento convencional
- variación de la tensión de vacío a carga
Los devandos presentes en un alternador son:
- devanado de inducido o de armadura
- devanado de excitación
En el caso del alternador trifásico el devanado de inducido se forma con tres devanados,
(fases distintas) cuyos terminales están dispuestos de la forma siguiente:
Las tres fases están conectadas a estrella dado que la conexión a triángulo se evita por la
posibilidad de corrientes de circulación interiores debidas a las f.e.m. inducidas, que resultan
en fase entre ellas. Estas armónicas no siempre están contenidas en valores suficientemente
modestos dada la dificultad para sacarle correctamente el perfil a los zapatos polares en
modo que la distribución del inductor en el entrehierro de lugar a formas de honda
perfectamente sinusoidales.
DE LORENZO
Sistemas para la
formación técnica
3
DL 1026A
El devanado de inducido, siendo previsto por la corriente nominal de erogación, tiene una
resistencia baja (su valor es proporcionalmente más pequeño mientras mayor sea la potencia
señalada en la placa de la máquina).
Naturalmente las tres fases deben presentar valores de resistencia prácticamente iguales y
por lo tanto se deberán tener en cuenta las pequeñas diferencias de los tres resultados
calculando una media aritmética.
El devanado de excitación normalmente presenta valores de resistencia más elevados, sobre
todo si la tensión de excitación es superior a 100 V.
La medida de la resistencia se debe efectuar en corriente continua y con la máquina parada.
De todas formas se debe actuar en una máquina que esté fría, es decir, que lleve varias horas
inactiva y de esta forma estar seguro que cada parte esté a temperatura ambiente. En este
caso si el método de medida no provocara un recalentamiento importante, se puede afirmar
que los valores de resistencia obtenidos son relativos a una temperatura de los devanados
igual a la del ambiente, que se puede medir fácilmente con un termómetro normal.
De los distintos métodos disponibles escogeremos el volt-amperimétrico.
Esquemas eléctricos para la medida de las resistencias de los devanados
Prueba Nº 1a
+
V
U1
V1
W1
-
A
V
= Resistencia de fase
I
Observaciones:
a) El voltímetro esta conectado después del amperímetro porque tal conexión, dado el valor
bajo de resistencia desconocida es sin duda preferible y vuelve completamente superflua
la corrección por el consumo de los instrumentos.
DE LORENZO
Sistemas para la
formación técnica
4
DL 1026A
b) El voltímetro, además de estar conectado después del amperímetro se encuentra
conectado directamente con los anillos de inducido sobre los cuales se apoyan las
escobillas. Lo anterior es absolutamente necesario para evitar contener también en la
medida la resistencia de contacto que está entre la escobilla y el anillo. En efecto esta
resistencia tiene un comportamiento anómalo y se valora en forma particular (ver el
calculo de las pérdidas en las escobillas para la determinación del rendimiento
convencional).
c) Eventulmente, es posible utilizar la resistencia de arranque del motor en serie al circuito
de medida para realizar una resistencia y de esta forma convertir la regulación de la
corriente en algo mas fácil.
Prueba Nº 1b
+
A
G
3~
U
V
V
-
W
V
= Resistencia del devanado de excitación
I
Observaciones
a) Se aconseja poner el voltímetro antes del amperímetro dado que el valor elevado de la
resistencia del devanado de excitación hace que tal conexión sea preferible porque
convierte en algo sin importancia la influencia del consumo de los instrumentos.
b) Además de lo anterior se aconseja conectar el voltímetro después de alimentar el circuito
y desconectarlo antes de la interrupción del circuito mismo.
En efecto, el devanado que se mide presenta un valor discreto de inductancia y las
bruscas variaciones de corriente pueden autoinducir las f.e.m. mucho más elevadas de la
tensión de medida a la cual es proporcional la portada del voltímetro.
DE LORENZO
Sistemas para la
formación técnica
5
DL 1026A
Página blanca
DE LORENZO
Sistemas para la
formación técnica
6
DL 1026A
PRUEBA
Nº 2
RELEVACION DE LAS CARACTERISTICAS DE MAGNETIZACION:
La característica de magnetización de un alternador y el diagrama que lo representa es el
flujo en salida de los polos inductores en función de la fuerza magnetómotriz de excitación.
En el lenguaje técnico normal es llamado con el mismo nombre también el diagrama que
tiene el mismo recorrido y es relevable en forma mas fácil.
La correspondencia perfecta de los dos diagramas citados resulta evidente considerando que:
a) La tensión V erogada al vacío de la máquina coincide perfectamente con la f.e.m.
inducida.
En el funcionamiento a velocidad constante esa resulta por lo tanto directamente
proporcional al flujo del inducido.
b) La corriente de excitación y la fuerza magnetomotriz difieren solamente por un
coeficiente representado por el numero de las espiras del devanado de los polos de
excitación.
La importancia de esta característica en la prueba del alternador es determinante en cuanto a
esa se hacen todos los métodos de determinación indirecta de las condiciones de
funcionamiento a carga, que se determinan con los procedimientos prevalentemente gráficos.
Esquema eléctrico para la relevación de las características de magnetización
Conexión del estator =
+
A
G
3~
M
U
f
V
W
-
V
NOTA : La prueba debe ser efectuada a velocidad nominal constante.
DE LORENZO
Sistemas para la
formación técnica
7
DL 1026A
Los resultados de la prueba permiten trazar la curva de magnetización
Observaciones:
a) La característica de magnetización va relevada a la velocidad de la placa de la máquina a
la cual corresponde la frecuencia de erogación nominal.
Si lo anterior no fuera posible, la medida puede ser efectuada pero con el cuidado de
reportar todos los resultados de prueba a la velocidad nominal mediante proporción lineal
simple.
En efecto siendo:
E1
E2
=
n1
; Vo = E
n2
resulta:
n2
V2 = V1
n1
DE LORENZO
Sistemas para la
formación técnica
8
DL 1026A
b) A diferencia que en la máquina a corriente continua el efecto del magnetismo residuo es
aquí normalmente poco importante. Esto se evidencia con el hecho que la tensión residua
tiene un valor en porcentaje modesto (en efecto la característica de magnetización parte
prácticamente desde el origen de los ejes) y de la falta de diferenciación entre
magnetización acendiente y descendiente.
La razón de este comportamiento esta en la medida del entrehierro que en los
alternadores se mantiene particularmente grande para reducir los efectos de la reacción
de armadura. Lo anterior es perfectamente válido para los alternadores que tengan
potencia superior a algunos kVA y pueda encontrar alguna excepción cuando la máquina
es muy pequeña. En este último caso, especialmente si los zapatos polares son macizos,
puede verificarse un magnetismo residuo que es bastante elevado.
c) Si el alternador es del tipo a polos salientes, la característica de magnetización relevada
hace referencia al flujo que recorre el circuito magnético de la máquina atravesando el
entrehierro en correspondencia de las expansiones polares inductoras.
En el funcionamiento al vacío el flujo existente en la máquina, siendo exclusivamente
producido por la excitación de los polos, sigue sin duda este recorrido.
El flujo provocado por la reacción de la armadura puede seguir recorridos diversos a
según del cosϕ de erogación. Para evaluar los efectos del amperio espiras de reacción de
la armadura, por lo tanto se puede utilizar la característica de magnetización solo cuando
el cosϕ de erogación no provoca desplazamientos angulares de las lineas de flujo y esto
sucede únicamente con cosϕ cercano a cero.
DE LORENZO
Sistemas para la
formación técnica
9
DL 1026A
Página blanca
DE LORENZO
Sistemas para la
formación técnica
10
DL 1026A
PRUEBA
Nº 3
MEDIDA DE LAS PERDIDAS MECANICAS EN EL HIERRO PERDIDAS
ADICIONALES
METODO DEL ARRASTRE DEL MOTOR EN PRUEBA
Durante el funcionamiento del alternador se verifican en su interior disipación de potencia
que son originadas por causas diversas.
El conocimiento del valor numérico de estas potencias pérdidas en las varias condiciones de
carga es indispensable para la determinación de la curva de rendimiento de la máquina.
Se tratará a continuación una prueba que permite medir los valores de las pérdidas
siguientes en el alternador:
a) Pérdidas mecánicas
Estas representan la potencia disipada de la parte rotativa por rozamiento en los soportes
y por ventilación.
Esta potencia está unida exclusivamente a la velocidad de rotación y no sufre cambios
apreciables en el paso de la máquina del funcionamiento al vacío al de carga (solamente
con máquinas de grandes dimensiones puede verificarse, en el paso a carga, una leve
variación de las pérdidas por rozamiento como consecuencia del diverso valor de las
solicitaciones en los soportes y al aumento inevitable de las vibraciones).
b) Pérdidas en el hierro
El circuito magnético de los polos está excitado con corriente continua y está por lo tanto
interesado a un flujo constante que no da lugar a pérdidas.
El hierro del circuito inducido, por efecto de la rotación se interesa a una magnetización
cíclicamente variable y por lo tanto es sede de disipaciones de potencia por histéresis
magnética y por corrientes parásitas de Focault.
Esta potencia disipada constituye la pérdida en el hierro del alternador; esta está
evidentemente unida al flujo que resulta y a la frecuencia erogada y por lo tanto a la
velocidad de rotación.
Por lo tanto lo que interesa no es solamente el solo flujo erogado por los polos sino el
que resulta de la composición de este último con el flujo de reacción de inducido.
Todavía, dado que sería extremamente complicado evaluar caso por caso (es decir por
cada valor de corriente y de cosϕ de erogación) la entidad de las reales pérdidas en el
hierro debidas a la efectiva conformación e itensidad del campo resultante, las normas
CEI han acordado lo siguiente:
1) Se considera pérdida en el hierro de los alternadores la que se verifica en el
funcionamiento al vacío con tensión y frecuencia nominales.
DE LORENZO
Sistemas para la
formación técnica
11
DL 1026A
2) Se tiene normalmente en cuenta la variación del flujo que resulta (y como
consecuencia pérdidas en el hierro) con el paso a carga, introduciendo el concepto de
las pérdidas adicionales.
Estas últimas dependen exclusivamente de la corriente de inducido y de estas se trata
en la voz que sigue c).
c) Pérdidas adicionales
Como ya dicho, estas deben tener en cuenta, así sea solo globalmente, el aumento de las
pérdidas en el hierro debidas a la alteración del campo magnético inductor en el pasaje
de vacío a con carga.
En estas se deben también englobar las causas siguientes de potencia pérdida (siempre de
entidad modesta, de determinación difícil y unidas exclusivamente a la corriente del
inducido) :
1) Pérdidas por corrientes parásitas generadas en las partes metálicas circustantes
(carrocería, estructuras.) DEL FLUJO DISPERSO DE LOS DEVANADOS inducidos.
2) Distribución no uniforme de la corriente en la sección transversal de los conductores
inducidos (efecto piel), causada esta también por el flujo de inducido que atropella los
conductores que lo generan.
Las normas CEI preveen que estas pérdidas adicionales sean medidas, en las diversas
corrientes del inducido, mediante prueba de funcionamiento en cortocircuito.
Esquema eléctrico con el método del arrastre del motor en prueba.
DE LORENZO
Sistemas para la
formación técnica
12
DL 1026A
PRUEBA Nº 1 - Pérdidas al vacío del motor en prueba
Cuando el motor en prueba está desconectado del alternador, haciendo girar al vacío a la
velocidad nominal del alternador absorve la potencia
P M = V M IM
que representa las pérdidas al vacío del motor en prueba excluyendo las de excitación.
PRUEBA Nº 2 - Pérdidas mecánicas del alternador
Después de haber acoplado el motor al alternador, se lleva el grupo a la velocidad nominal
del alternador, poniendo este último desexcitado.
La potencia absorvida por el motor resultará
P'M = V'M
•
I'M
y representará la suma de las pérdidas mecánicas del motor y del alternador. En efecto el
motor debe arrastrar también el alternador que, siendo desexcitado, necesita únicamente sus
pérdidas mecánicas.
Dado que el motor trabaja en las mismas condiciones de la prueba Nº 1 (la misma tensión
del inducido, la misma velocidad, corriente del inductor apenas un poco mayor) se puede
admitir que sus pérdidas queden inalteradas y considerar por lo tanto las pérdidas mecánicas
del alternador igual a
Pm = P'M - P M
PRUEBA Nº 3 - Pérdidas en el hierro del alternador
Con el motor acoplado al alternador, se lleva el grupo a la velocidad nominal del alternador
y se le regula su excitación de esta forma haciendo erogar al vacío su tensión nominal.
La nueva potencia absorvida del motor resulta
P " M = V"M
•
I"M
y será ligeramente aumentada con respecto al valor relevado en la prueba Nº 2 con
referencia al motor este esta ahora cargado también en las pérdidas en el hierro del
alternador.
Todavía admitiendo que las pérdidas del motor en prueba no estén variadas las pérdidas en
el hierro del alternador resultan
P hierro = P"M
- Pm
- PM
DE LORENZO
Sistemas para la
formación técnica
13
DL 1026A
Prueba Nº 4 - Pérdidas adicionales en el alternador
Después de haber cerrado en cortocircuito el inducido,
:manteniendo constante la velocidad al valor nominal,
valores de corriente oportunos, se releva la característica
interesa evaluar la potencia absorbida por el motor
cortocircuito:
este resultará
se remite en rotación el grupo
excitando el alternador con los
de cortocircuito. En esta prueba
dados los diversos valores de
P"' M = V"' M • I"'M
Reteniendo que son transcurables las pérdidas en el hierro, dada la modesta entidad del flujo
que resulta, se puede calcular
P"'M - P M = pérdidas mecánicas + pérdidas en el cobre y en el alternador
y por lo tanto las pérdidas en el cobre resultan ligeramente superiores a las calculables
comenzando por los valores de las resistencias de los devanados inducidos (prueba práctica
Nº 1) y de la corriente de cortocircuito hecha circular durante la medida.
Las pérdidas adicionales, correspondientes a la corriente de inducido Icc resultan dadas por
P add = Pcu - 3 R f • I
2
ccf
NOTA : Como conclusión de lo ya expuesto, toda la prueba se basa sobre la admisión de
que las pérdidas del motor de arrastre no sufran cambios fundamentales en el
paso del funcionamiento al vacío al funcionamiento con la pequeña carga del eje
constituido por las pérdidas (mecánicas y en el hierro o sino mecánicas y en el
cobre) del alternador.
Tal admisión es válida en cuanto más grande sea la potencia de placa del motor
con respecto al valor de las pérdidas del alternador. En práctica esta es ya
completamente aceptable cuando la potencia de la placa del motor es igual a la
del alternador.
En el caso en el cual no se disponga un motor de potencia suficiente, se debe
tener en cuenta la variabilidad de su rendimiento y por tal razón debe ser clara la
curva que suministra η = f(Pabs ).
En este último caso el motor se denomina motor calibrado, este puede tener
también una potencia reducida con repecto al generador en prueba; en efecto es
suficiente que este suministre a las pérdidas de la máquina en arrastre cuyo valor
no supere el 20 - 25% de la potencia de placa.
DE LORENZO
Sistemas para la
formación técnica
14
DL 1026A
Los resultados de la prueba Nº 4 en cortocircuito evidencian gráficamente el
comportamiento de las pérdidas adicionales al variar de la corriente de inducido, así como se
ilustra en el diagrama.
Pcu
f = Hz
3R • I
2
Pérdida addicional
I
DE LORENZO
Sistemas para la
formación técnica
15
DL 1026A
Página blanca
DE LORENZO
Sistemas para la
formación técnica
16
DL 1026A
PRUEBA
RELEVACION
DE
LA
PERMANENTE TRIFASICA
CARACTERISTICA
DE
Nº 4
CORTOCIRCUITO
La característica de cortocircuito de un alternador trifásico es el diagrama que expresa el
valor de la corriente de cortocircuito permanente trifásica en función de la corriente de
excitación.
Este diagrama es indispensable para la aplicación de los principales métodos de prueba
indirecta del alternador.
Esquema eléctrico para la relevación de las características de corto circuito.
Conexión del estator =
+
A
G
3~
M
U
V
W
-
Ai
Después de haber regulado la velocidad del grupo al valor de la velocidad nominal del
alternador, se revelan los pares de valores de las corrientes de armadura (Ai) en función de
la corriente de excitación (A).
Los resultados de la prueba permiten trazar la característica de corto circuito.
DE LORENZO
Sistemas para la
formación técnica
17
DL 1026A
Icc
n=
Iexc
Observaciones:
a) La corriente de inducido que se considera en la prueba es la correspondiente al
cortocircuito permanente trifásico. En otras palabras:
- los valores de la corriente de cortocircuito es la de régimen alcanzado y no debe ser
confundida con la transitoria de cortocircuito que se verifica cuando la máquina ya
excitada es puesta bruscamente en cortocircuito.
- el cortocircuito que se considera es el trifásico es decir simétrico. Con este propósito
se debe tener presente que en el caso que sean puestas en corto circuito una o dos
fases solamente, la reacción de armadura asimétrica da lugar a un campo invertido
notable qué puede inducir tensiones elevadas en las fases abiertas.
b) El gráfico Icc =f (iecc) tiene una marcha lineal y pasa por el origen de los ejes.
Este hecho se explica si se considera que la impedencia propia de las fases es
fuertemente inductiva y por lo tanto la corriente de cortocircuito resulta fuertemente
swatada con respecto a la tensión al vacío inducida y determina una reacción de
armadura casi completamente desmagnetizada.
DE LORENZO
Sistemas para la
formación técnica
18
DL 1026A
En este caso:
- el flujo total en el interior de la máquina, a pesar de las corrientes de excitación
bastante elevadas, resulta siempre muy reducido:su valor debe dar lugar a un f.e.m.
inducida suficiente a equilibrar la sola caída de tensión ZIcc debida a la impedencia
propia de las fases. El circuito magnético trabaja por lo tanto a lo largo del primer
trecho de la característica de magnetización cuya marcha es rectilíneo y por lo tanto se
debe admitir
ϕ = Ki exc ; I c c =
E
E
=
Z
K"ϕ
=
K'
= K"'iexc
K'
donde
K, K', K", K''' = son constantes de proporcionalidad
- la corriente de cortocircuito provocada por la f.e.m. residuo, ya de por si muy modesta
en los alternadores, se reduce todavía más por la reacción desmagnetizadora de la
armadura que tiende a anular el flujo residuo. Por lo tanto se puede admitir con grande
aproximación que la característica de cortocircuito pasa por el origen de los ejes.
NOTA : El modesto valor de potencia del alternador puede atenuar la rigidez de lo
expuesto: de esta forma puede verificarse un magnetismo residual
suficientemente elevado para provocar una corriente débil de cortocircuito
aún en ausencia de excitación.
c) Así como se verifica experimentalmente, la corriente de cortocircuito esta unida
únicamente al valor de la corriente de excitación y es ampliamente independiente de la
velocidad.
Este hecho, aparentemente extraño, se explica fácilmente si se considera que la
impedencia propia de las fases tiene la componente resistiva prácticamente sin
importancia con respecto a la componente reactiva.
Por lo anterior se puede admitir que
Z ≅X
E
Ic c =
Z
≅
E
Kϕf
=
X
K 'ϕn
=
2πfL
K"Ln
Al variar la velocidad del alternador varían por lo tanto en la misma proporción lineal
sea E que X y por lo tanto su raporto, que representa la corriente de cortocircuito, queda
constante.
Solamente a velocidad bastante reducida la frecuencia puede resultar tan baja que reduce
fuertemente el valor de X y no convertir en algo sin importancia la componente resistiva
de las fases.
NOTA : La prueba para la relevación de la característica de cortocircuito es por lo
tanto válidamente realizable aún en el caso en el cual no se disponga de un
motor anterior en grado de arrastrar el alternador a su velocidad de placa.
DE LORENZO
Sistemas para la
formación técnica
19
DL 1026A
Página blanca
DE LORENZO
Sistemas para la
formación técnica
20
DL 1026A
PRUEBA
Nº 5
ARRASTRE DE LA CURVA DE IMPEDENCIA SINCRONICA METODO DE
BEHN - ESCHEMBURG
Entre las curvas de funcionamiento práctico de un alternador, toman una importancia
particular, como para todos los generadores eléctricos, los siguientes:
- CARACTERISTICA EXTERNA : esta evidencia en cual medida la corriente de carga
provoca una variación de la tensión erogada.
- CARACTERISTICA DE REGULACION : esta evidencia en cual medida se debe
intervenir con la regulación, automática o manual, sobre la excitación, cuando se desee
mantener constante la tensión erogada, al variar de la corriente de carga.
Estas curvas fundamentales no siempre pueden relevar experimentalmente por la gran
dificultad de conseguir las cargas y el motor adecuados al alternador en prueba sobre todo
cuando la potencia en juego asume valores relevantes.
De esta forma se han ideado métodos de prueba indirecta que, con aproximaciones de
diferente entidad, permiten determinar las curvas ya citadas sin tener que efectuar la prueba
a carga efectiva.
Entre estos métodos trataremos los siguientes:
- método de BEHN-ESCHEMBURG
- método de POTIER
El método de Behn da resultados diversos de la verdad especialmente con alternadores a
polos salientes pero es seguido igualmente, porque es bastante simple, cuando interesa
conocer el orden de grandeza de los valores en juego.
El método de Potier es más preciso, aunque su aplicación resulta un poco mas trabajosa.
DE LORENZO
Sistemas para la
formación técnica
21
DL 1026A
SIGNIFICADO Y DETERMINACION DE LA IMPEDENCIA SINCRONA
Metodo de Behn-Eschemburg
El método de Behn-Eschemburg se basa en la siguiente consideración simplificativa:
En el funcionamiento al vacío el alternador presenta en sus bornes la entera f.e.m. generada.
En el funcionamiento la carga de tensión en los bornes del alternador varía porque las fases
internas, teniendo una impedencia equivalente llamada impedencia sincrona, provoca caídas
de tensión.
La tensión en salida de los bornes se calculerá en cualquier condición de carga restando
vejatoriamente la caída de tensión sobre la impedencia sincrona interna a la f.e.m. generada
al vacío.
Esquematizando y considerando una única fase se tiene
V AB = E o - Zs I
Para poder aplicar prácticamente el método descrito se debe conocer el valor numérico de la
impedencia sincrónica Zs y con esta finalidad se recurre a una prueba al vacío y a una en
cortocircuito.
En efecto, aplicando el pensamiento simplificado de Behn-Eschemburg al funcionamiento en
cortocircuito del alternador se puede escribir
V AB = 0
Zs = E o/I c c
donde
Eo = f.e.m. inducido en la fase de cortocircuito y relevable sobre la característica
de magnetización en correspondencia al valor de la corriente de excitación
realizada.
Icc = corriente de cortocircuito correspondiente a la excitación que ha producido Eo
DE LORENZO
Sistemas para la
formación técnica
22
DL 1026A
Repitiendo este cálculo por diversos valores de la corriente de excitación se puede trazar la
curva de impedencia sincrónica.
Iexc
(A)
Eo
(V)
Icc
(A)
Zs
(Ω)
Observaciones
a) El diagrama evidencia claramente que el valor de la impedencia sincrónica no es
constante. En efecto la impedencia sincrónica está fuertemente unida al efectivo grado de
saturación magnética de la máquina la cual en cualquier condición de funcionamiento
depende:
- del valor de la corriente de excitación
- del valor de la corriente de carga
- del valor del cosϕ de carga
El método de determinación de la curva Zs = f(iecc) seguido no permite conocer la unión
de Zs con el cosϕ de erogación en cuanto Zs esta determinada por un cosϕ de
cortocircuito qué es bastante cercano a cero; contrariamente resulta evidenciado la unión
de Zs con las corrientes de excitación y de carga.
Para escoger el valor de la impedencia que se debe usar en los cálculos se prosigue en la
forma siguiente:
- se releva el valor Z's que corresponde a la corriente de excitación nominal
(posiblemente con referencia al cosϕ que interesa en los calculos)
- se releva el valor Z"s correspondiente a la corriente nominal de inducido (Icc = In)
- de los dos valores considerada la aproximación por exceso del método, se utiliza el
que resulta menor.
DE LORENZO
Sistemas para la
formación técnica
23
DL 1026A
b) La impedencia sincrónica determinada de esta forma puede ser fácilmente descompuesta
en sus dos componentes, en cuanto se conoce el valor de la resistencia de la fase prueba
Nº 1:
Xs = √ Zs - R
2
2
Naturalmente, dado que R es constante, también la reactancia X resultará dependiente de
iecc e del cosϕ.
Analizando los valores numéricos de R y Zs nos podemos dar cuenta que estas
pertenecen a órdenes de magnitud distintas y precisamente Zs tiene valores más elevados
de R.
Por esta razón considerando la ya notable tolerancia del método, se prefiere ignorar el
término R y evaluar la impedencia sincrónica como reactancia.
El procedimiento de cálculo resultará de esta forma más semplificado mientras que los
resultados no sufrirán cambios apreciables.
DE LORENZO
Sistemas para la
formación técnica
24
DL 1026A
PRUEBA
Nº 6
CARACTERISTICAS DE REGULACION CON EL METODO INDIRECTO DI
BEHN-ESCHEMBURG
Se trata de determinar indirectamente las características de regulación del alternador.
Como ya explicado anteriormente, las curvas de funcionamiento de los alternadores deben
en práctica ser casi siempre determinadas por vía indirecta porque la prueba de carga
efectiva presenta, en la mayor parte de los casos, grandes dificultades.
Esquematizando la idea de Behn teniendo en cuenta los elementos de la anterior prueba 5,
se obtiene el siguiente esquema equivalente por cada fase del alternador, donde se supone
que Zs ≅ Xs
Si ahora imaginamos que el alternador suministre una corriente genérica de fase I con un
cosϕ genérico entonces se puede escribir
V (AB) + X s x I =
Eo
DE LORENZO
Sistemas para la
formación técnica
25
DL 1026A
y esta relación esta representada con el diagrama vectorial
Eo
XsI
V
ϕ
I
donde el vector XsI se ha trazado a 90 grados en anticipación sobre la corriente I, como
sucede en cada reactancia puramente inductiva.
Si, como en nuestro caso, se quiere determinar cual debe ser la corriente de excitación del
alternador para que la tensión de los bornes asuma un cierto valor V cuando el alternador
eroga una cierta corriente I sobre una carga que tiene un cosϕ genérico, es suficiente trazar
en escala el diagrama vectorial reportado arriba y determinar graficamente el valor de Eo.
Sobre la característica de magnetización se relevara después, en correspondencia del valor
Eo, la corriente de excitación necesaria.
Para el arrastre de la entera curva de regulación, que hace referencia a la tensión nominal y
cosϕ = 0.8 con retraso, se procede de la forma siguiente:
a) Se fija una escala de tensiones adecuadas y se representan los valores de los vectores de
fase de la tensión nominal y de la corriente nominal desfasados del ángulo relativo;
b) Se calcula el valor c.d.t. XsIn y se reporta, en la escala de las tensiones, sobre el
diagrama vectorial.
Se obtiene así el vector de la f.e.m. de fase Eon;
DE LORENZO
Sistemas para la
formación técnica
26
DL 1026A
c) Sobre la característica de magnetización se individua en correspondencia de Eon, el valor
de la corriente de excitación necesaria a la máquina en esta condición de carga;
d) Se consideran sucesivamente corrientes de erogación de fase igual a:
1/4 I n ;
2/4 In;
3/4 I n;
5/4 In .
y para cada una de estas el valor de la c.d.t. XsI que varía en la misma proporción de las
corrientes, mientras que queda inalterada la dirección del vector que las representa, así
como no varía la tensión Vn y el ángulo ϕ.
La f.e.m. Eo correspondiente a cada cuarto de la carga completa puede ser por lo tanto
fácilmente determinada dividiendo en cuatro partes iguales el vector XsIn y
congregandolas en el punto 0;
e) Para cada valor de Eo se revela sobre la característica de magnetización el valor
correspondiente de la corriente de excitación.
f) Se puede trazar la curva de regulación iecc = f(I) para cosϕ = 0.8.
g) Queriendo determinar las características de regulación correspondientes a otros cosϕ, es
suficiente proceder en el mismo modo variando únicamente la posición angular entre los
vectores V y I.
DE LORENZO
Sistemas para la
formación técnica
27
DL 1026A
h) Diagrama vectorial para cosϕ = 1
i) Diagrama vectorial para cosϕ = 0.8 en anticipación
DE LORENZO
Sistemas para la
formación técnica
28
DL 1026A
La característica de regulación asume la marcha indicada en el gráfico siguiente:
DE LORENZO
Sistemas para la
formación técnica
29
DL 1026A
Observaciones:
1) La marcha de las curvas de regulación resulta en subida por el funcionamiento a
cosϕ = 1 y cosϕ = 0.8ret y parcialmente en "bajada" para el funcionamiento a
cosϕ = 0.8adel.
2) Las curvas de regulación sacadas con el método de Behn no resultan completamente en
coincidencia con las efectivas porque el método se basa en semplificaciones que resultan
algunas veces excesivas (especialmente con alternadores a polos salientes) y llevan a
tener en cuenta las caídas de tensión superiores a las reales.
En particular:
- La impedencia sincrónica, que Behn considera para evaluar globalmente los efectos de
la reacción de armadura sobre la tensión erogada, debería asumir valores diversos a
según de las condiciones de excitación y de carga consideradas, en cuanto es diferente
el nivel de saturación del circuito magnético de la máquina.
Esto convertiría en inaplicable el método y por lo tanto se acepta tener constante el
valor de Zs.
- El método para determinar la impedencia sincrónica utiliza una prueba de
cortocircuito a la que corresponde una reacción de armadura fuertemente
desmagnetizadas (cosϕcc = 0) y como consecuencia un débil grado de saturación del
circuito magnético.
Los valores de Zs calculados de esta forma por lo tanto resultan muy abundantes,
especialmente con respecto a los que se refieren a funcionamientos con cosϕ (factor
de potencia) próximos a 1 o también con anticipo.
- En el caso de alternadores con polos salientes hay que tener en cuenta que al cambiar
el cosϕ de la carga también cambia el entrehierro que interesa las amperio-vueltas de
reacción de armadura. En efecto, con corriente desfasada de 90° los polos magnéticos
de reacción de armadura se encuentran en eje con los inductores y por lo tanto el
entrehierro que los interesa es mínimo; con corrientes en fase, la reacción de armadura
en cambio presenta los polos magnéticos desfasados con respecto a los inductores y
por lo tanto interesados por el entrehierro interpolar que es netamente mayor.
El método de determinación de Zs mediante una prueba de cortocircuito, a la que
corresponde un cosϕ = 0, nos lleva en estos casos a introducir un posterior motivo de
aproximación por exceso.
NOTA:
Al analizar los resultados numéricos de la aplicación del método de
Behn-Eschemburg, hay que tener bien presente que el modesto valor de la
potencia nominal de la máquina ensalza las citadas razones de escasa
aproximación ínsitas en el método mismo.
Por lo tanto dicho método asume, en nuestro caso, un valor puramente
orientativo.
DE LORENZO
Sistemas para la
formación técnica
30
DL 1026A
PRUEBA
CARACTERISTICAS EXTERIORES
BEHN - ESCHEMBURG
CON
EL
METODO
Nº 7
INDIRECTO
DE
Este método trata de determinar las características exteriores del alternador.
Como ya mencionado con anterioridad, en este caso también el procedimiento de cálculo es
prevalentemente gráfico y se basa en el simple concepto de la impedancia sincrónica
ampliamente visto en precedencia.
Esquematizando el razonamiento de Behn-Eschemburg mencionado anteriormente en las
anteriores pruebas Nº 5 y Nº 6, la tensión en vacío del alternador resulta:
Si, como en este caso, interesa determinar como cambia el vector VAB, partiendo de una
tensión Eo constante, cuando la carga provoca la variación del vector XsI, se puede proceder
de la siguiente manera, referido a un cosϕ = 0,8 con retraso:
a) Trazar, aunque no sea en escala, el vector representativo de la corriente de plena carga.
b) Calcular el valor de la c.d.t. XsIn y fijada una conveniente escala de tensiones,
representar el vector a 90° con adelanto sobre el vector In, como debe ser una
inductancia pura.
c) Desde el vértice del vector XsIn, trazar, en la escala de tensiones, el vector representativo
de la tensión nominal Vn con la angulación deseada con respecto al vector de la
corriente.
DE LORENZO
Sistemas para la
formación técnica
31
DL 1026A
d) El vector resultante XsIn + Vn representa la f.e.m. Eon de la máquina:
cos ϕ = 0.8ret
V5/4
r
V4/4
V3/4
V2/4
V1/4
5/4
Vo = E on
4/4
X sIn
3/4
2/4
1/4
ϕ = 36
. 52'
cosϕ = 0.8
0
I
e) Con centro en 0 trazar un arco en círculo con un radio r = Eon.
f) Subdividir el vector XsIn en 4 partes iguales y alargarlo hasta los 5/4.
g) De los distintos cuartos de XsIn trazar paralelas al vector Vn.
h) Los puntos de intersección de las paralelas con el círculo de Eo señalan los vectores de
las tensiones erogadas en los distintos cuartos de plena carga.
Estos vectores se pueden medir fácilmente, convertidos en voltios a través de la escala de
tensiones y representados en el diagrama V = f(I).
i) Si se quisieran determinar las características exteriores correspondientes a otros cosϕ, es
suficiente proceder de la misma manera solo que cambiando la posición angular entre los
vectores V e I.
DE LORENZO
Sistemas para la
formación técnica
32
DL 1026A
l) Diagrama de Behn-Eschemburg para cosϕ = 1:
cosϕ = 1
r
V5/4
V4/4
5/4
V3/4
4/4
X sIn
V2/4
3/4
V1/4
2/4
V o = Eon
1/4
0
I
m)Diagrama de Behn-Echemburg para cosϕ = 0,8 con adelanto:
cosϕ = 0.8adel
5/4
V5/4
4/4
X sIn
3/4
2/4
V4/4
1/4
V3/4
0
I
V2/4
V1/4
Vo = E on
r
DE LORENZO
Sistemas para la
formación técnica
33
DL 1026A
Las características exteriores asumen las indicaciones siguientes expresadas en el gráfico:
Observaciones:
1) La evolución de las características exteriores resulta "cadente" para los funcionamientos
con cosϕ = 1 y cosϕ = 0,8 retraso y en "aumento" para el funcionamiento con cosϕ = 0,8
adelanto.
2) Las características exteriores correspondientes a cosϕ = 1 y cosϕ = 0,8 retraso no
coinciden perfectamente con las efectivas, como ya hemos visto en la prueba Nº 6.
DE LORENZO
Sistemas para la
formación técnica
34
DL 1026A
PRUEBA
Nº 8
RELIEVE DE UN PUNTO DE LA CARACTERISTICA DE CARGA SIN
VATIOS.
DETERMINACION DE LOS COEFICIENTES Xd y
SEGUN POTIER
Como ya hemos visto anteriormente existen numerosas razones que hacen que sea más bien
escasa la aproximación de los resultados obtenidos con el método Behn-Eschemburg.
Dicho método, en el intento de simplificar el procedimiento de cálculo, se aleja
excesivamente de la realidad de los fenómenos que están ligados al paso de vacío a carga
del alternador.
En particular se puede notar que:
- En el funcionamiento en vacío la f.e.m. Eo erogada se debe únicamente al flujo inductor
provocado por la corriente de excitación de los polos. Pasando a carga, también el
inducido crea amperio-vueltas que se componen vectorialmente con la de los polos. El
flujo que resulta de esta forma asume un valor que también puede ser muy diferente
(normalmente menor) con respecto al existente en vacío y por consiguiente la f. e. m.
generada asume un valor E distinto de Eo.
- Dicha f.e.m. de carga no resulta por entero aplicable a los bornes ya que encuentra las
caídas de tensión típicas de todos los bobinados inducidos de corriente alterna:
a) C.d.t. óhmica debida a la resistencia equivalente R de inducido.
b) C.d.t. inducida debida a la reactancia de dispersión Xd del inducido que tiene en
cuenta la porción de flujo generado por la corriente de carga que no "reacciona" con
el flujo inductor sino que se encierra alrededor de los cabezales de los bobinados o
pasa directamente de un diente de inducido al otro sin atravesar el entrehierro. Dicha
reactancia de dispersión Xd es naturalmente mucho menor que la reactancia sincrónica
Xs según Behn-Eschemburg, que también abarcaba los efectos del flujo de reacción de
armadura.
El método de tratamiento ideado por Potier analiza por separado los efectos citados y por
consiguiente nos lleva a resultados más cercanos al verdadero.
Para la aplicación del método de Potier hay que determinar:
- La resistencia R de inducido, fácilmente medible (prueba Nº 1).
- La reactancia de dispersión Xd de inducido.
- El coeficiente α de proporcionalidad que "traduce" la corriente de inducido en corriente
de excitación equivalente desde el punto de vista del flujo generado. De tal manera se
podrá fácilmente efectuar la composición de las amperios-vueltas de inducido con las
inductoras.
Para determinar los valores de Xd y de α hay que realizar una prueba de carga con cosϕ = 0
con retraso y aplicar el procedimiento gráfico ilustrado más adelante.
DE LORENZO
Sistemas para la
formación técnica
35
DL 1026A
Esquema eléctrico para la medición de las características de carga sin vatios:
Conexión
estator =
Conexióndel
inducida
+
A2
G
3~
M
W
V
U
-
✱
V
✱
✱
✱
A1
Carga inductiva
Carga
inducida
DE LORENZO
Sistemas para la
formación técnica
36
DL 1026A
PROCEDIMIENTO GRAFICO PARA DETERMINAR Xd y α
1) De las anteriores pruebas Nº 2 y 4 deducir las características de magnetización y de
cortocircuito y representarlas sobre un único sistema de ejes cartesianos.
2) En correspondencia al valor OA de la corriente de excitación realizada durante la
medición de cosϕ ≅ 0, representar el valor AB de la tensión de fase medida en la misma
prueba.
DE LORENZO
Sistemas para la
formación técnica
37
DL 1026A
3) Localizar en la característica de cortocircuito el valor de la corriente de excitación OC
correspondiente a la corriente de inducido realizada en la prueba a cosϕ ≅ 0.
4) Del punto B llevar hacia el origen y paralelamente al eje de las abcisas, un segmento
BD = OC.
5) Del punto D trazar una paralela al trazado inicial, prácticamente rectilínea, de
características de magnetización hasta que encuentre la misma característica en el punto E.
6) Del punto E bajar una vertical localizando de esta forma el punto F y el triángulo de
Potier EFB.
7) Medir el segmento EF, que representa la tensión de reactancia que se refiere a la
corriente obtenida en la prueba de cosϕ = 0, y después de haberlo traducido en voltios a
través de la escala de las tensiones, se calcula:
EF (V)
Xd =
= …… Ω de fase
I (A)
8) Medir el segmento BF, que representa la reducción de magnetización debida a la
reacción de inducido referida a la corriente de prueba, y después de haberlo convertido
en amperios a través de la escala de las corrientes, se calcula:
α =
BF (V)
= ……
I (A)
Observaciones:
1) La condición de funcionamiento que se ha representado en el punto B se ha deducido de
una erogación en cosϕ ≅ 0 con retraso porque en dicho caso se pueden admitir las
siguientes simplificaciones que se han aplicado para deducir los valores de Xd y α :
a) La relación vectorial:
E = V + RI + XdI
dada la particular posición angular de los vectores representativos y la modesta
entidad de RI, se puede reconducir, con bastante aproximación, a una simple relación
numérica:
E = V + Xd I
y todo esto se evidencia con claridad en el diagrama vectorial siguiente:
DE LORENZO
Sistemas para la
formación técnica
38
DL 1026A
E
XdI
RI
E ≅ V + Xd • I
Xd ≅
V
0
E-V
I
I
b) Las amperio-vueltas de reacción provocadas por una corriente desfasada de 90° con
retraso se presentan exactamente contrarias a las inductoras (corrientes de inducido no
en cuadratura en cambio darían lugar a amperio-vueltas de reacción angularmente
desplazadas en el entrehierro con respecto a las inductoras).
Con erogación en cosϕ = 0 la composición entre estas amperio-vueltas por lo tanto se
traduce en una simple diferencia numérica.
2) Con el fin de evitar equivocaciones de interpretación y para no introducir inútiles
complicaciones, aconsejamos "limar" los trazados iniciales de las características de
magnetización y de cortocircuito de manera que empiecen en el origen de los ejes aún si
los resultados de prueba pongan en evidencia un sensible campo magnético residual.
Como ya hemos ampliamente demostrado, el magnetismo residual en efecto puede
asumir valores importantes solamente en alternadores de potencia muy pequeña.
DE LORENZO
Sistemas para la
formación técnica
39
DL 1026A
Página blanca
DE LORENZO
Sistemas para la
formación técnica
40
DL 1026A
PRUEBA
Nº 9
CARACTERISTICAS DE REGULACION CON EL METODO INDIRECTO DE
POTIER
Se analiza el funcionamiento de carga del alternador según el método de Potier, teniendo en
consideración una sola fase, como se usa para todas las máquinas y circuitos simétricos y
equilibrados, en la hipótesis que se conozcan V, I, cosϕ y que interese determinar el valor
de la corriente de excitación Ie :
DE LORENZO
Sistemas para la
formación técnica
41
DL 1026A
Lo primero de todo se pueden trazar en escala los vectores representativos de la tensión V y
de la corriente I y por lo tanto calcular las caídas de tensión de fase RI y XdI y traducirlas
en vectores según las escalas prefijadas.
La f.e.m. inducida de carga se localizará por la suma vectorial:
E = V + RI + X dI
Esta f.e.m. está producida por el flujo resultante cuyo vector representativo se encuentra por
lo tanto a 90° de adelanto sobre la misma.
En fase con el flujo resultante también se encuentra el vector representativo de las
amperio-vueltas resultantes en cuyo lugar sin embargo es preferible considerar el vector de
la corriente de excitación equivalente total It.
El valor de la corriente It se puede localizar fácilmente en la característica de magnetización
en correspondencia del valor E y representado en el diagrama vectorial después de haber
fijado una adecuada escala para las corrientes de excitación.
Conociendo el valor del coeficiente α de Potier se pueden calcular las amperio-vueltas de
reacción de inducido o, mejor, la corriente de excitación Ir equivalente, desde el punto de
vista magnético, a la corriente de inducido.
Por lo tanto la corriente:
Ir = α
•
I
es convertible en un vector, en fase con la I, mediante la escala de las corrientes de
excitación prefijada.
Resulta determinante en este momento el valor efectivo Ie de la corriente de excitación del
alternador mediante simple diferencia vectorial.
En efecto resulta:
It = Ie + Ir
y por lo tanto:
I e = I t - Ir
PROCEDIMIENTO
REGULACION
DE
CALCULO
PARA
LAS
CARACTERISTICAS
DE
En este apartado se trata de repetir la construcción vectorial vista con anterioridad, para
distintos valores de la corriente de carga I, de donde normalmente se consideran los
diferentes cuartos, manteniendo inalteradas la tensión y el cosϕ.
1) Se representa en primer lugar el diagrama vectorial relativo a la corriente nominal.
2) Se subdivide el vector ZIn en sus cuartos y se localizan las correspondientes E.
3) Para cada valor de E se determina It, se calcula Ir y se realiza la composición vectorial
que lleva a determinar Ie.
En las páginas que siguen se pueden ver los diagramas vectoriales relativos a los
mencionados tres cosϕ límite de erogación.
DE LORENZO
Sistemas para la
formación técnica
42
DL 1026A
cosϕ = 0.8ret
E5/4
E3/4
E2/4
Vphase = ……
- Ir
XdIn
E1/4
It
RIn
En
Ie
V
. 52 '
ϕ = 36
I
αIn = Ir
cosϕ = 1
- Ir
It
Vphase = ……
E5/4
E3/4
Ie
E2/4
E1/4
En
XdIn
V
RIn
I
DE LORENZO
Sistemas para la
formación técnica
43
DL 1026A
cosϕ = 0.8adel
- Ir
Vphase = ……
It
Ie
36
. 52 '
I
En
E3/4
V
E5/4
E2/4
XdIn
E1/4
DE LORENZO
Sistemas para la
formación técnica
44
RIn
DL 1026A
Gráfico:
Con la ayuda de los valores vistos en los diagramas de las fuerzas magnetomotrices se
pueden trazar las curvas de regulación:
Iexc
V = Vphase = ……
f = …… Hz
cosϕ = 0.8ret
cosϕ = 1
cosϕ = 0.8adel
I
0
1/4 In
2/4 In
3/4 In
4/4 In
5/4 In
Observaciones:
Las curvas determinadas con el método de Potier se desplazarán de las efectivas en menor
medida de las deducidas según el método de Behn-Eschemburg debido a la ya discutida
mayor aproximación del método de Potier.
Dicho método, prácticamente riguroso en el caso de alternadores con inductores lisos, cae
ligeramente en error cuando se aplica a alternadores con polos salientes. Efectivamente en
estos el entrehierro no es constante y las relaciones de armadura con cosϕ próximos a la
unidad, desarrollándose en el amplio vacío interpolar, tienen una eficacia efectivamente
menor.
Las caídas de tensión calculadas con este método por lo tanto resultan ligeramente
abundantes, sobre todo si se refieren a cosϕ de erogación superior a 0,8.
DE LORENZO
Sistemas para la
formación técnica
45
DL 1026A
Página blanca
DE LORENZO
Sistemas para la
formación técnica
46
DL 1026A
PRUEBA
CARACTERISTICAS
POTIER
EXTERIORES
CON
EL
METODO
Nº 10
INDIRECTO
DE
Las características exteriores del alternador se pueden determinar de manera parecida a la
usada para la determinación de las características de regulación.
La dificultad ahora será de naturaleza geométrica en cuanto se conocen los valores de ϕ, I,
Ie pero no se conoce la posición angular de E y por lo tanto no es fácil la construcción del
diagrama vectorial.
Entonces lo que conviene es calcular las distintas curvas de regulación referidas al cosϕ que
nos interesa pero diferenciadas por un valor distinto de la tensión de erogación (por ejemplo
se pueden fijar tensiones iguales a 80 - 100 - 120 - 140 - 160 % del valor de matrícula).
En correspondencia con el valor de Ie del que nos interesa conocer la característica exterior
se traza una paralela al eje de las abscisas.
Los puntos de intersección con las curvas de regulación nos dan los pares de valores de V e
I que permiten trazar las características exteriores.
DE LORENZO
Sistemas para la
formación técnica
47
DL 1026A
El valor Vo de la ordenada en el origen se puede fácilmente deducir de la característica de
magnetización en correspondencia al valor de Ie prefijado.
La característica exterior asume la marcha indicada:
Para determinar otra característica exterior correspondiente al mismo cosϕ pero con un valor
distinto de Ie, hay que desplazar la paralela de la abscisa, que sale de Ie, que interseca las
distintas curvas de regulación.
Naturalmente, si queremos cambiar el valor del cosϕ de referencia de la característica
exterior, habrá que volver a calcular una nueva serie de características de regulación
referidas al nuevo valor del cosϕ y proceder en el modo ya visto.
DE LORENZO
Sistemas para la
formación técnica
48
DL 1026A
PRUEBA
LOCALIZACION
EXTERIORES
DIRECTA
DE
ALGUNAS
Nº 11
CARACTERISTICAS
Como ya hemos visto en la prueba Nº 5, la característica exterior del alternador es una curva
de funcionamiento entre las más importantes para la máquina. Esta evidencia en que medida
cambia la tensión erogada al cambiar la corriente solicitada por la carga, permaneciendo
invariados los valores de la corriente de excitación y del cosϕ de erogación.
Efectivamente es evidente que no solo la corriente de inducido sino también la corriente de
excitación y el cosϕ de la carga intervienen sobre el valor de la tensión erogada, la primera
cambiando el valor de Eo y la segunda provocando una distinta configuración del campo de
reacción inducido.
Por lo tanto existen infinitas características exteriores (normalmente su conjunto se
denomina "familia") correspondientes cada una de ellas a una distinta corriente de excitación
y; por lo tanto, a un diferente valor de tensión en vacío.
A igualdad de corriente de excitación existe además otra familia de características, también
bastante numerosa, en la que cada una de ellas se diferencia de la otra por un distinto cosϕ
de carga.
En práctica, sin embargo, nos interesan casi exclusivamente las características
correspondientes a corrientes de excitación nominal y; entre estas, las correspondientes a los
siguientes cosϕ de erogación que "delimitan" el normal campo de variabilidad:
cosϕ = 1
cosϕ = 0,8 con retraso
DE LORENZO
Sistemas para la
formación técnica
49
DL 1026A
Las características exteriores asumen la marcha indicada en el siguiente gráfico:
Las características exteriores permiten determinar la variación de tensión de vacío a plena
carga.
a) con cosϕ = 1:
∆V = V"o - Vn
b) con cosϕ = 0,8 retraso:
∆V = V'o - Vn
que normalmente se representan en tanto por ciento:
∆V
v% =
• 100
Vn
Observaciones:
1) La marcha de las características exteriores sin lugar a dudas resulta cadente en cuanto,
como ya sabemos, las reacciones de armadura provocadas por corrientes
óhmico-inductivas son generalmente desmagnetizantes.
En el funcionamiento con erogaciones capacitativas la marcha de las características
exteriores podría resultar creciente en cuanto la reacción de armadura, en este caso
magnetizante, podría compensar con abundancia la caída de tensión provocada por la
resistencia y por la reactancia de dispersión de los bobinados.
2) La característica exterior para cosϕ = 0,8 retraso evidencia caídas de tensión
decisivamente mayores de las relativas a cosϕ = 1.
En efecto en este último caso, la reacción de armadura desarrolla sobre el flujo de los
polos una acción generalmente "torcida" sin reducir sensiblemente el valor.
DE LORENZO
Sistemas para la
formación técnica
50
DL 1026A
PRUEBA
Nº 12
RELIEVE DIRECTO DE ALGUNAS CARACTERISTICAS DE REGULACION
Como ya hemos mencionado en la prueba Nº 5, la característica de regulación de un
alternador es el diagrama que evidencia en que medida hay que regular la corriente de
excitación para mantener constante la tensión erogada en las distintas condiciones de carga.
La importancia práctica de esta regulación es notable en cuanto los usos normales no
admiten variaciones de las tensiones de alimentación si no es dentro de unos límites muy
estrechos (normalmente no más del ± 5%).
La regulación naturalmente se podrá realizar manualmente mediante la intervención
automática de adecuados aparatos.
Es natural que exista una perfecta analogía con cuanto ya dicho en referencia de las
características exteriores (prueba Nº 11). Cada alternador por lo tanto presenta una infinidad
de características de regulación diferenciadas entre si por un distinto valor de tensión
erogada que hay que mantener constante (entre estas la más importante es sin lugar a dudas
la que se refiere al valor nominal).
A igualdad de tensión que hay que mantener constante, existen además infinitas
características de regulación diferenciadas por el valor de cosϕ de erogación que se
considera y; entre estas, las correspondientes a los siguientes cosϕ de erogación que
"delimitan" el normal campo de variabilidad:
cosϕ = 1
cosϕ = 0,8 con retraso
DE LORENZO
Sistemas para la
formación técnica
51
DL 1026A
Las características de regulación asumen la marcha indicada por el siguiente gráfico:
Observaciones:
1) La característica de regulación para cosϕ = 0,8 retraso resulta más "alta" de la de
cosϕ = 1, como era fácil de suponer por la marcha de las relativas características
exteriores.
2)
Ambas curvas de regulación evidencian la necesidad de aumentar la corriente de
excitación de manera más que proporcional a medida que la carga aumenta.
Esto se debe a la progresiva saturación del circuito magnético causada por el valor
cada vez mayor que viene soloicitado al flujo de los polos para compensar las c.d.t.
crecientes.
3)
El valor de la corriente de excitación a plena carga debe resultar idéntico, a no ser que
existan tolerancias contructivas, al señalado en la matrícula del alternador.
DE LORENZO
Sistemas para la
formación técnica
52
DL 1026A
PRUEBA
Nº 13
RENDIMIENTO CONVENCIONAL DEL ALTERNADOR
El rendimiento de una máquina eléctrica se puede determinar de dos formas:
- con el método directo
- con el método indirecto
a) Método directo:
Este método consiste en poner en funcionamiento la máquina mediante condiciones de
carga deseadas y medir ya sea la potencia absorbida que la potencia dada; el rendimiento,
deducible de su relación, comúnmente se llama "efectivo".
Dicho método acarrea serias dificultades de medición y prácticamente solo se puede
aplicar a máquinas de modesta potencia; efectivamente:
- si la máquina de prueba es de tipo giratorio, una de las dos potencias que hay que
medir es mecánica lo que constituye sin lugar a dudas una grave complicación de
medida.
- si la máquina de prueba es de potencia lo suficientemente elevada, además de la gran
dificultad de encontrar la carga mecánica o eléctrica adecuada, tendremos una
excesiva incidencia de inevitables errores de medida sobre el resultado final.
En estos casos, en efecto, la potencia dada y la potencia absorbida tienen valores
porcentualmente poco distantes entre ellos.
b) Método indirecto:
Este método en cambio llega a la determinación del rendimiento sin cargar efectivamente
la máquina sino siguiendo una serie de medidas que permiten determinar el valor de las
pérdidas de potencia en las distintas condiciones de funcionamiento.
Conocidas las pérdidas, es fácil alcanzar el valor de rendimiento.
Este método es aconsejable particularmente cuando la máquina de prueba es de potencia
superior a una decina de kW y es de más sencilla aplicación que el método directo.
Sin embargo hay que tener en cuenta que no todas las pérdidas de potencia se pueden
determinar rigurosamente y que los distintos procedimientos de medida pueden llevar a
resultados ligeramente alejados. Por lo tanto será necesario atenerse a convenciones
normalizadas que hagan comparables los resultados finales de las distintas pruebas de
ensayo.
Como consecuencia de este modo de actuar, el valor de rendimiento así determinado se
denomina "convencional".
DE LORENZO
Sistemas para la
formación técnica
53
DL 1026A
PROCEDIMIENTO DE CALCULO
Las Normas establecen que para el cálculo del rendimiento convencional de un alternador se
tengan que considerar las siguientes pérdidas:
1 Pérdidas mecánicas y en el hierro.
Se tienen que valorar a velocidad de matrícula y a tensión nominal y considerar
constantes durante el paso de vacío a carga.
2 Pérdidas en cobre inducido.
Apreciables mediante la fórmula:
3 Ri I
2
donde
Ri = resistencia de fase del bobinado inducido, medida a la temperatura convencional de
75° C.
I = corriente de fase del inducido correspondiente a la condición de carga considerada.
3 Pérdidas por excitación.
Corresponden a la potencia total absorbida por el circuito de excitación en las
condiciones de carga considerada. Dicha potencia se disipa completamente por efecto de
Joule, en parte en el bobinado de excitación y en parte en eventuales reóstatos de
regulación.
Suponiendo que el alternador funcione en tensión nominal con cualquier condición de
carga, los valores de las corrientes de excitación correspondientes a las distintas
corrientes de inducido se pueden deducir de las curvas de regulación, determinables,
estas también, por método indirecto (pruebas Nº 6 y 7).
Si, además, el circuito de excitación está alimentado por una fuente independiente con
tensión V constante, la potencia total absorbida por el mismo cuando lo atraviesa una
genérica corriente de excitación i, es:
P exc = V
•
i
4 Pérdidas en las escobillas.
El alternador, si no es del tipo de rueda polar con imanes permanentes, está siempre
dotado de colector de anillos para poder acceder a los terminales del bobinado situado en
la parte giratoria.
Las escobillas que se apoyan sobre los anillos determinan una caída de tensión anormal
con respecto a la ley de Ohm y de valor prácticamente constante cuando las atraviesa
corriente y por tal razón la pérdida correspondiente convencionalmente se mide en:
(Vatios totales) 2 • i
donde i es la corriente de excitación en (A), admitiendo que dicha pérdida no se haya
comprendido ya entre las producidas por excitación.
DE LORENZO
Sistemas para la
formación técnica
54
DL 1026A
5 Pérdidas adicionales.
De estas ya hemos habado en la prueba n. 3 y se ha evidenciado su dependencia de la
corriente de inducido.
Dada su modesta entidad y lo complejo de su relación con la temperatura, las Normas
recomiendan medirlas a temperatura de prueba sin aplicar ninguna corrección.
6 Tabla de calculos
Normalmente el cálculo del rendimiento convencional se realiza para los siguientes
valores de corriente de inducido:
0;
1/4 I n;
2/4 I n;
3/4 I n;
4/4 In ;
5/4 In
y repetidos para los dos valores límites de cosϕ (1 y 0,8 retraso).
El resumen de las tablas de cálculos está especificado en las páginas siguientes.
DE LORENZO
Sistemas para la
formación técnica
55
DL 1026A
cosϕ = 0.8ret;
conex = star;
V exc = …… (V)
en
vacío
1/4 de
carga
2/4 de
carga
3/4 de
carga
aplena
carga
5/4 de
carga
Tensión
erogada
(Volt)
Corriente
erogada
(Amp)
1
Corrientedeexcit.
(Amp)
2
Potenciade
rendimiento
(Vat)
3
Pérdidasmecánicasy
enhierro(Vat)
4
Pérdidasdeexcit.
(Vat)
5
Pérdidasenlas
escobillas
(Vat)
0
0
0
6
Pérdidasenelcobre
inducido
(Vat)
7
Pérdidas
adicionales
(Vat)
8
Potencia
absorbida
(Vat)
Rendimiento
(%)
REFERENCIAS :
1)
2)
3)
4)
5)
6)
7)
8)
Deducirse de las curvas Iexc = f (I) calculadas en la prueba Nº 9.
Calcularse con la fórmula P = √3 VI cosϕ
Deducirse de la prueba Nº 3.
Calcularse con la fórmula P exc = Vexc i exc, donde Vexc = Volt.
Calcularse con la fórmula P sp = 2 • I exc
2
Calcularse con la fórmula P j = 3 RI ; donde R = resistencia de fase inducida a 75°C.
Deducirse de la prueba Nº 3.
Calcularse sumando a la potencia de rendimiento todas las pérdidas.
DE LORENZO
Sistemas para la
formación técnica
56
DL 1026A
cosϕ = 1;
conex = star;
Vexc = …… (V)
en
vacío
1/4 de
carga
2/4 de
carga
3/4 de
carga
aplena
carga
5/4 de
carga
Tensión
erogada
(Volt)
Corriente
erogada
(Amp)
1
Corrientedeexcit.
(Amp)
2
Potenciade
rendimiento
(Vat)
3
Pérdidasmecánicasy
enhierro(Vat)
4
Pérdidasdeexcit.
(Vat)
5
Pérdidasenlas
escobillas
(Vat)
6
Pérdidasenelcobre
inducido
(Vat)
7
Pérdidas
adicionales
(Vat)
8
Potencia
absorbida
(Vat)
0
0
0
Rendimiento
(%)
REFERENCIAS :
1)
2)
3)
4)
5)
6)
7)
8)
Deducirse de las curvas Iexc = f (I) calculadas en la prueba Nº 9.
Calcularse con la fórmula P = √3 VI cosϕ
Deducirse de la prueba Nº 3.
Calcularse con la fórmula P exc = Vexc i exc, donde Vexc = Volt.
Calcularse con la fórmula P sp = 2 • I exc
2
Calcularse con la fórmula P j = 3 RI ; donde R = resistencia de fase inducida a 75°C.
Deducirse de la prueba Nº 3.
Calcularse sumando a la potencia de rendimiento todas las pérdidas.
DE LORENZO
Sistemas para la
formación técnica
57
DL 1026A
Gráfico:
DE LORENZO
Sistemas para la
formación técnica
58
DL 1026A
PRUEBA
PARALELO DEL ALTERNADOR CON
REGULACION DEL CAMBIO DE P Y Q
LA
RED
TRIFASICA
Nº 14
DE
Una maniobra que se realiza frecuentemente en una central eléctrica es la conexión de los
alternadores en paralelo con la red de distribución de la energía.
Actualmente las redes de distribución locales están todas interconectadas entre si de manera
que cubran el entero territorio nacional; la red nacional se conecta preferentemente con la de
los paises fronterizos para un intercambio de la energía eléctrica producida, mediante un
común y esplícito acuerdo de un bien de consumo.
Después de la instalación en paralelo, el solo alternador de central por lo tanto se encuentra
conectado a un circuito en el que ya están erogando un gran número de otros alternadores y
de los que se extraen una gran cantidad de cargas, con un juego de potencias generalmente
más elevado con respecto a la máxima erogada por el mismo.
Las consecuencias de esta desproporción de potencias son:
a) La red "impone" al alternador conectado a la misma su valor de tensión y de frecuencia;
dichos valores no podrán mutar ni siquiera cuando se modifique la corriente de
excitación de los polos o el par motriz del eje de la máquina.
b) Cualquier maniobra que pretenda cambiar tensión y frecuencia del alternador en cambio
producirá una variación de la potencia reactiva y de la potencia activa intercambiada
entre las máquinas y la red.
Dado el modesto valor de su potencia de matrícula, desde el instante de la conexión a la red,
el alternador se encontrará sometido a los mismos lazos de funcionamiento de los
alternadores de central y por lo tanto podrá verificarse experimentalmente cuanto dicho
anteriormente en los puntos a y b.
La conexión del alternador en paralelo con la red se puede realizar, sin provocar un violento
cortocircuito, solamente cuando:
1 La frecuencia del alternador es igual a la de la red.
2 La tensión del alternador es igual a la de la red.
3 Los vectores de las tensiones del alternador y de la red coinciden con la fase.
4 El sentido cíclico de las tensiones del alternador coincide con el de las tensiones de red.
DE LORENZO
Sistemas para la
formación técnica
59
DL 1026A
La condición indicada en el punto 4 es una directa consecuencia de la aplicación, en las tres
tensiones de fase, de la condición indicada en el punto 3.
Para verificar la igualdad de los puntos 1 y 2 es suficiente con un frecuencímetro y un
voltímetro conmutables; la coincidencia de las fases en cambio se puede medir mediante
especiales instrumentos indicadores (sincronoscopios de índice) o también mediante la
señalación de bombillas adecuadamente introducidas (sicronoscopios con luces giratorias o
de luces batientes).
ESQUEMA ELECTRICO para el paralelo del alternador con la red
Conexión inducida
DE LORENZO
Sistemas para la
formación técnica
60
DL 1026A
El instante de la operación de paralelo es aquél en el que la bombilla L1 está apagada y se
verifica la igualdad de las tensiones y de la frecuencia.
1 - El alternador ahora está conectado en paralelo con la red y, si las maniobras se han
realizado correctamente, estará completamente en equilibrio. El amperímetro y los
vatímetros conectados entre la máquina y la red evidenciarán por lo tanto que no
existe intercambio de corriente y de potencia.
2 - Si a continuación probamos a aumentar la velocidad de rotación del motor antes
regulando su excitación, se verá que la velocidad permanece constante.
El amperímetro y los vatímetros indican en este momento un intercambio de corriente
y de potencia que aumenta durante esta regulación (habrá que tener cuidado de no
superar el valor nominal de corriente del alternador para no acercarse demasiado al
límite de estabilidad de la máquina).
De esta forma se podrá verificar que:
a) La potencia real Wa + Wb resulta positiva lo que significa que la misma fluye del
alternador hacia la red (la posición de los bornes diferenciados por las bobinas
amperométricas y voltimétricas de los vatímetros conectados en el circuito no
permite ninguna duda a este respecto).
b) La potencia reactiva √3 (Wa - Wb) intercambiada entre la máquina y la red es muy
modesta y no cambia apreciablemente durante esta regulación.
3 - Reduciendo ahora la excitación del primer motor se nota que la velocidad permanece
constante mientras que disminuyen corriente y potencia hasta volver a ser nulas como
en el momento del paralelo (punto 1).
Si se prosigue con la disminución de la excitación del primer motor para reducir la
velocidad, se notará el renacer de un intercambio de corriente y de potencia real entre
máquina y red pero esta vez la suma Wa + Wb resulta negativa.
La potencia en juego ahora va de la red a la máquina que por lo tanto está
funcionando con motor sincrónico.
4 - Retornando a las condiciones de paralelo, anulando de nuevo el intercambio de
corriente y potencia, si ahora se aumenta o disminuye la corriente de excitación del
alternador se puede verificar la tensión erogada no cambia sino que nace nuevamente
un intercambio de corrientes y de potencias entre máquina y red (tampoco en este
caso conviene superar los valores de corriente nominal).
De esta forma se podrá observar que:
a) La potencia real Wa + Wb intercambiada entre máquina y red es muy modesta y no
cambia apreciablemente durante la regulación de la excitación del alternador.
b) La potencia reactiva √3 (Wa - Wb) intercambiada entre máquina y red cambia
notablemente como consecuencia de la regulación de la excitación del alternador.
Se puede verificar fácilmente, también, que dicha potencia reactiva inductiva asume
valores positivos, es decir fluye del alternador hacia la red, cuando la corriente de
excitación se aumenta, mientras que en cambio asume valores negativos, es decir
fluye de la red hacia el alternador, cuando la corriente de excitación se disminuye.
DE LORENZO
Sistemas para la
formación técnica
61
DL 1026A
Conclusiones:
De los resultados de la prueba se pueden sacar las siguientes conclusiones:
1 - El intercambio de las potencias, real y reactiva, entre un alternador y la red con el que
está conectado en paralelo (teniendo esta última una potencia instalada predominante
se puede regular a gusto mediante simples maniobras sobre el primer motor o sobre el
circuito de excitación.
2 - Variando el par motriz desarrollado por el motor primero se modifica casi por
completo el intercambio de potencia real entre máquina y red mientras que no cambia
apreciablemente el intercambio de potencia reactiva.
3 - Variando la corriente de excitación se modifica el intercambio de potencia reactiva
entre máquina y red mientras que no cambia con claridad el intercambio de potencia
real.
4 - Actuando contemporáneamente sobre el motor primero y sobre la excitación, se
pueden regular los valores de las potencias P y Q en juego y de esta manera erogar al
alternador el cosϕ deseado.
DE LORENZO
Sistemas para la
formación técnica
62
DL 1026A
PRUEBA
Nº 15
CURVA EN "V" O DE MORDEY DEL MOTOR SINCRONICO
En la prueba Nº 14 hemos podido ver que para regular el intercambio de potencia activa
entre alternador y red conectados en paralelo hay que actuar únicamente sobre el primer
motor.
También se ha verificado que desactivando el primer motor, o todavía más, frenando el eje
del alternador, se obtiene el paso automático de este último al funcionamiento con motor
sincrónico, con desarrollo de par motriz.
Uno de los sistemas para poner en rotación como motor una máquina sincrónica es,
efectivamente, el de hacerla funcionar preventivamente como alternador, efectuar el paralelo
con la red y por lo tanto desactivar el motor propulsor. Esta operación bastante complicada
se hace necesaria en cuanto el motor sincrónico prácticamente no dispone de par de
aceleración de salida y por lo tanto no se pondría en marcha si lo alimentáramos con rotor
parado sin adoptar particulares artificios. En efecto el motor sincrónico tiene un
comportamiento "rígido" y puede funcionar solo a una velocidad rigurosamente constante,
independiente ya sea del cargo que de la tensión de alimentación y ligada únicamente a la
frecuencia f y al número p de polos según la relación :
120
n =
•
f
(rpm)
p
Sin ambargo se puede intuir que si durante el funcionamiento el par de frenado aumentase
más que el valor del par motriz máximo desarrollable por el motor, estos se pararían
bruscamente (comúnmente se dice que "pierde el paso") y la corriente absorbida aumentaría
a valores muy elevados.
Una característica singular del motor sincrónico consiste en la posibilidad de regular dentro
de amplios límites el valor de la corriente absorbida y del cosϕ de absorción, en cualquier
condición de carga, actuando únicamente sobre la corriente de excitación. Es también
posible, siempre regulando la excitación, hacer de manera que la absorción se realice con
desfases en adelanto, realizando de esta forma un comportamiento capacitativo.
El diagrama I = f (Iexc) que evidencia esta unión se denomina normalmente curva en "V"
por su típica marcha,o curva de Mordey. Naturalmente existen un gran número de curvas en
"V" caracterizadas cada una por un distinto par resistente en el eje; entre estas tiene gran
importancia la relativa al funcionamiento en ausencia de par de frenado ya que se refiere al
empleo, bastante frecuente, del motor sincrónico en calidad de reajustador giratorio.
DE LORENZO
Sistemas para la
formación técnica
63
DL 1026A
El esquema eléctrico que hay que realizar es parecido al de la prueba Nº 14
tan solo intercambiando los bornes voltimétricos de los vatímetros para tener una indicación
positiva de la potencia Wa + Wb si fluye de la red a la máquina.
Después de haber realizado el paralelo del alternador con la red, se desexcita el motor
propulsor y se verifica que la velocidad de rotación no cambie.
1 - A desarrollar el par motriz necesario para el movimiento del grupo ahora se encarga el
alternador; este efectivamente ha pasado automáticamente a funcionar de motor
sincrónico como resulta claramente de la indicación de los vatímetros que detectan
una potencia real de flujo de la red hacia la máquina.
2 - Al aumentar la excitación en la máquina resultará Wb > Wa y esto indicará, estando
el circuito seguramente simétrico y equilibrado, que la absorción se realiza con cosϕ
en adelanto.
El comportamiento del motor es por lo tanto de tipo capacitativo.
3 - Reduciendo a continuación la excitación disminuye la corriente absorbida hasta
alcanzar un valor mínimo, para después empezar a aumentar, determinando de esta
forma la típica forma en "V" del diagrama I = f (i).
Dado que también las indicaciones de los vatímetros sufren notables cambios resulta
también una variación del cosϕ de absorción: con corriente de excitación menor de la
necesaria para obtener la mínima corriente absorbida resulta Wb < Wa lo que
evidencia que la absorción se realiza ahora con cosϕ en retraso.
El comportamiento del motor por lo tanto es de tipo inductivo.
4 - En condiciones de funcionamiento correspondiente al paso del comportamiento
capacitativo al inductivo, se puede observar que Wb = Wa, es decir el motor
sincrónico absorbe con cosϕ = 1 como un cargo perfectamente óhmico.
Dicha condición se verifica prácticamente en correspondencia con la mínima
absorción de corriente.
DE LORENZO
Sistemas para la
formación técnica
64
DL 1026A
Gráfico.
Observaciones:
1 Si sobre el mismo diagrama cartesiano se representan ambas curvas:
Iabs = f(iexc)
cosϕ = f(Iexc)
resulta evidenciado con claridad la amplia posibilidad de regulación que se puede aplicar
en la absorción del motor sincrónico actuando tan solo sobre su corriente de excitación.
En particular se puede notar que:
a) Existe un valor de corriente de excitación i(1) al que corresponde una absorción
perfectamente en fase (cosϕ = 1).
En dichas condiciones la corriente absorbida adopta prácticamente el valor mínimo.
b) Con excitaciones superiores a i (1), las corrientes de inducido son absorbidas con
desfases en adelanto, mientras que con excitaciones inferiores a i (1) las corrientes de
inducido son absorbidas con desfases en retraso.
Ya sea en uno que en otro caso, especialmente con pequeños pares de frenado en el
eje, los cosϕ se pueden regular hasta valores notablemente inferiores: esta
particularidad es muy útil en el caso del empleo del motor sincrónico como
reajustador de fase giratorio.
2 La tensión de alimentación tendría que permanecer constante durante toda la prueba.
En realidad se puede verificar una variación, también sensible, debida a la incidencia de
las caídas de tensión de la red de alimentación. Estas últimas asumen, efectivamente,
valores muy distintos durante las mediciones ya que son elevadas en la base de
excitación (los absorbimientos están muy desfasados en retraso) y modestas, si no
negativas, a las fuertes excitaciones (los absorbimientos en este caso están muy
desfasados en adelanto).
El diagrama de todas formas se referirá al valor medio de la tensión de prueba.
DE LORENZO
Sistemas para la
formación técnica
65
DL 1026A
3 A pesar de la rigurosa constancia de la potencia de rendimiento durante la prueba, se
notará que la potencia absorbida (especialmente en el caso de la curva en "V" en vacío)
sufrirá importantes mutamentos.
Esto es debido a las variaciones de las pérdidas en el cobre y en el hierro de la máquina
como consecuencia de la amplia excursión de valores de corriente, ya sea de inducido
que de excitación, y del flujo resultante.
4 Como ya hemos mencionado, la curva en "V" se refiere a un funcionamiento con par
resistente, y por lo tanto potencia de rendimiento, constante. La detectada en este párrafo
corresponde a par de rendimiento, y por lo tanto potencia de rendimiento, prácticamente
nula, es decir, con funcionamiento en vacío del motor sincrónico.
Si el motor sincrónico se frenase con distintos valores de par resistente, se podrían
detectar la misma cantidad de curvas en "V" que resultarían más altas de la de vacío y
ligeramente corridas hacia la derecha, como indicado en el diagrama.
DE LORENZO
Sistemas para la
formación técnica
66
DL 1026A
EJERCICIOS
PRACTICOS
DE LORENZO
Sistemas para la
formación técnica
67
DL 1026A
Página blanca
DE LORENZO
Sistemas para la
formación técnica
68
DL 1026A
DATOS
DE
PLACA
GENERADOR SINCRONICO TRIFASICO DL 1026A
20 Viale Romagna - 20089 ROZZANO (Milano) ITALY
Código del motor
3~G
Corriente
Tensión generada
Factor de potencia
Potencia nominal
Frecuencia
Corriente de excitación
-1
Velocidad (min )
Tensión de
excitación
Clase de aislamiento
Grado de protección
DE LORENZO
Sistemas para la
formación técnica
69
DL 1026A
Página blanca
DE LORENZO
Sistemas para la
formación técnica
70
DL 1026A
PRUEBA
PRACTICA
Nº 1
Medida de la resistencia de los bobinados de inducido y de excitación
a) Medida de la resistencia de los bobinados de inducido:
DE LORENZO
Sistemas para la
formación técnica
71
DL 1026A
Sucesión de las maniobras.
Después de haber realizado el circuito marcado a rayas, efectuar las siguientes maniobras:
1 Preparar los mandos de los módulos:
SALIDA CC VARIABLE:
(Excitación)
REOSTATO DE ARRANQUE:
Interruptor abierto.
Convertidor girado completamente en
sentido antihorario
Max. resistencia
2 Activar el módulo de alimentación
3 Mediante la manivela regular la corriente en el amperímetro A hasta obtener una
corriente de 0,3 A.
4 Medir las indicaciones del amperímetro A y del voltímetro V.
5 Abrir el interruptor y repetir las operaciones 1 hasta 4 para los otros terminales U2-U1 y
V2-V1.
TABLA DE RELIEVES
Temperatura de prueba: °C
Terminales
Amperímetro
(A)
W1 - W2
U1 - U2
V1 - V2
Fórmulas de cálculo:
V
R =
I
RU + RV + RW
Rm =
3
DE LORENZO
Sistemas para la
formación técnica
72
Voltímetro
(V)
Rphase
(Ω)
Rm
(Ω)
DL 1026A
b) Medida de la resistencia de los bobinados de excitación.
DE LORENZO
Sistemas para la
formación técnica
73
DL 1026A
Sucesión de las maniobras.
Después de haber realizado el circuito a rayas, efectuar las siguientes maniobras:
1 Preparar los mandos de los módulos:
SALIDA CC VARIABLE:
(Excitación)
Interruptor abierto.
Convertidor girado completamente en
sentido antihorario.
2 Activar la salida cc variable
3 Mediante la manivela regular la corriente en el amperímetro A hasta obtener una
corriente de 0,2 A.
4 Medir las indicaciones del amperímetro A y del voltímetro V.
TABLA DE RELIEVES
Temperatura de prueba = …… °C
Amperímetro
(A)
V
Rexc =
I
DE LORENZO
Sistemas para la
formación técnica
74
Voltímetro
(V)
Rexc
(Ω)
DL 1026A
PRUEBA
PRACTICA
Nº 2
Relieve de las caracteristicas de magnetización
DE LORENZO
Sistemas para la
formación técnica
75
DL 1026A
Sucesión de las maniobras.
Después de haber realizado el circuito a rayas, efectuar las siguientes maniobras:
1 Preparar los mandos de los módulos:
SALIDA CC VARIABLE:
(Excitación)
Interruptor abierto.
Convertidor girado completamente en
sentido antihorario.
SALIDA CC VARIABLE:
Interruptor abierto.
Salida a 220V aprox.
REOSTATO DE ARRANQUE:
Resistencia max.
REOSTATO DE EXCITACION:
Resistencia min.
2 Activar el motor de arrastre hasta lograr la velocidad nominal del alternador.
3 Activar la salida cc variable (excitación).
4 Mediante la manivela regular la corriente de excitación aumentandola hasta aprox. el
20-30 % más allá del valor nominal.
5 Por cada valor de corriente de excitación (amperímetro A) medir las indicaciones
correspondientes de la tensión de salida a través del voltímetro V2.
6 Desexcitar el alternador y bloquear el motor.
Tabla de relieves:
I exc
(A)
DE LORENZO
Sistemas para la
formación técnica
V2
(V)
76
f
(Hz)
n
(rpm)
DL 1026A
PRUEBA
PRACTICA
Nº 3
Medida de las perdidas mecanicas, en el hierro y adicionales
DE LORENZO
Sistemas para la
formación técnica
77
DL 1026A
Sucesión de las maniobras:
PRUEBA Nº 1 - PERDIDAS EN VACIO DEL MOTOR DE ARRASTRE.
Nota: El motor tiene que estar desconectado del alternador.
Realizar las conexiones relativas tan solo al motor de arrastre y preparar los mandos de los
módulos:
1 Preparar los mandos de los módulos:
SALIDA CC VARIABLE:
(Excitación)
Interruptor abierto.
Convertidor girado completamente en
sentido antihorario.
SALIDA CC VARIABLE:
Interruptor abierto.
Salida a 220V aprox.
REOSTATO DE ARRANQUE:
Resistencia max.
REOSTATO DE EXCITACION:
Resistencia min.
2 Poner en derivación el amperímetro A1 realizando la conexión a rayas de manera que se
pueda proteger contra la punta de corriente durante el arranque.
3 Activar el módulo de alimentación accionando el interruptor.
El motor de corriente continua tiende a ponerse en marcha.
Verificar que el sentido de rotación del motor sea correcto y quitar la derivación.
Posicionar el conmutador Ra de la posición "1" a la posición "6".
4 Regular el convertidor hasta que la tensión de alimentación del motor sea igual al valor
indicado en la placa y con el reostato de excitación regular la velocidad de rotación al
valor nominal de la velocidad del alternador.
5 Medir las indicaciones de los instrumentos A1 y V1.
6 Parar el motor abriendo el interruptor.
DE LORENZO
Sistemas para la
formación técnica
78
DL 1026A
PRUEBA Nº 2 - PERDIDAS MECÁNICAS DEL ALTERNADOR.
Nota : El motor se tiene que conectar al alternador. El alternador no debe estar excitado.
Repetir la operación del módulo de control de la prueba Nº 1
1 Reavivar el motor y llevarlo a la velocidad nominal del alternador repitiendo los puntos
del 1 al 5 de la prueba Nº 1.
PRUEBA Nº 3 - PERDIDAS EN EL HIERRO DEL ALTERNADOR.
1 Conectar mecánicamente el alternador al motor.
Conectar solamente el voltímetro V2.
2 Repetir las operaciones 1 y 4 de la prueba Nº 1.
3 Cuando la volocidad de rotación corresponda exactamente a la velocidad nominal, excitar
el alternador hasta que la tensión de salida corresponda al valor nominal.
Controlarla mediante el voltímetro V2.
4 Medir la tensión de entrada y la corriente del motor.
PRUEBA Nº 4 - PERDIDAS ADICIONALES DEL ALTERNADOR.
Nota : El motor tiene que estar conectado al alternador. Conectar solo el amperímetro A2
y conectar U1 a V1. Repetir la operación del módulo de control de la prueba Nº 1
1 Arrancar el motor como en la prueba Nº 1.
3 Cuando la volocidad de rotación corresponda exactamente a las velocidades nominales,
excitar el alternador hasta que la tensión de salida en cortocircuito sea aprox. 120% de
las nominales.
Controlarla mediante el amperímetro A2.
3 Medir las indicaciones de la tensión de entrada y de la corriente al motor.
4 Repetir las mediciones por valores decrecientes de la corriente erogada.
5 Parar el motor abriendo el interruptor.
DE LORENZO
Sistemas para la
formación técnica
79
DL 1026A
Tabla de relieves
n = …… rpm
Pérdidas del alternador
N
Voltímetro
V1 (V)
Amperímetro
A1 (A)
Amperímetro
2
A2 (A)
Pm Pir Pcu 3RI
(W) (W) (W) (W)
1
---
--- --- ---
---
Padd
(W)
Notas
---
Solo motor
en vacío
2
---
--- ---
---
---
Motor +
alternador
desexcitado
3
---
---
---
---
Motor +
alternador
excitado
4
---
5
---
6
---
7
---
8
---
DE LORENZO
Sistemas para la
formación técnica
80
Motor +
alternador en
cortocircuito
DL 1026A
PRUEBA
PRACTICA
Nº 4
Relieve de las caracteristicas de cortocircuito
DE LORENZO
Sistemas para la
formación técnica
81
DL 1026A
Sucesión de las maniobras.
Después de haber realizado el circuito a rayas, efectuar las siguientes maniobras:
1 Preparar los mandos de los módulos:
SALIDA CC VARIABLE:
(Excitación)
Interruptor abierto.
Convertidor girado completamente en
sentido antihorario.
SALIDA CC VARIABLE:
Interruptor abierto.
Salida a 220V aprox.
REOSTATO DE ARRANQUE:
Resistencia max.
REOSTATO DE EXCITACION:
Resistencia min.
2 Activar el motor de arrastre hasta lograr la velocidad nominal del alternador.
3 Cerrar el interruptor del módulo de salida cc variable (excitación) y regular la manivela
hasta obtener la corriente nominal del alternador.
4 Por cada uno de los diferentes valores de la corriente de excitación medir la
correspondiente corriente de armado.
5 Cuando la corriente de armado esté bastante cerca del valor nominal, cambiar la
velocidad de rotación dentro de una amplia gama y verificar que la corriente de
cortocircuito esté bastante constante.
6 Desexcitar el alternador y parar el motor.
Tabla de relieves:
Corriente de
cortocircuito
I cc
(A)
DE LORENZO
Sistemas para la
formación técnica
82
Corriente de
excitación
Iex c
(A)
n
(rpm)
Notas
DL 1026A
PRUEBA
PRACTICA
Nº 5
Relieve de las caracteristicas exteriores
La finalidad de esta prueba es la de relevar las características exteriores, es decir las curvas
que unen la tensión a la corriente erogada por cosϕ = 1 y cosϕ = 0,8 inductivo.
Esquema eléctrico
+
A2
Ra
-
+
Re
F1
G
3~
M
V1
F2
L
✱
-
W
V
Wa
U
✱
✱
Wb
✱
V2
F
A1
R
Nota : El alternador tiene que funcionar a su velocidad nominal mientras que la carga
esté cambiando.
DE LORENZO
Sistemas para la
formación técnica
83
DL 1026A
PROTECCION
SOBRE
VELOCIDAD
SALIDA CC VARIABLE
SALIDA CC VARIABLE
(Excitación)
K1
+
-
V1
M
250V
Reóstato de arranque
Carga resistiva
Carga inductiva
Reóstato de excitación
✱
✱
Frecuencia de red
V2
Wa
400V
2A - 400V
✱
Wb
2A - 400V
Transductor
óptico
W2
U2
V2
K2
U1
V1
W1
F1
✱
F2
A1
2A
+
-
A2
rpm
K1
K2
0.6A
Medidor de velocidad
DE LORENZO
Sistemas para la
formación técnica
84
DL 1026A
A) Punto de la caracteristica de la corriente devatiada (wattless)
Sucesión de las maniobras.
Después de haber realizado el circuito a rayas, efectuar las siguientes maniobras :
1 Preparar los mandos de los módulos:
SALIDA CC VARIABLE:
(Excitación)
Interruptor abierto.
Convertidor girado completamente en
sentido antihorario.
SALIDA CC VARIABLE:
Interruptor abierto.
Salida a 220V aprox.
REOSTATO DE ARRANQUE:
Resistencia max.
REOSTATO DE EXCITACION:
Resistencia min.
2 Activar el motor de arrastre hasta lograr la velocidad nominal del alternador.
3 Cerrar el interruptor del módulo de salida cc variable y regular la manivela hasta obtener
la corriente nominal del alternador.
4 Posicionar los conmutadores solo del módulo de la carga L en la posición "1" (después
en 2, después en 3, ……).
Controlar que la velocidad sea estable (eventualmente cambiar la excitación del motor) y
la excitación del alternador de manera que la tensión de salida esté cerca del valor
nominal.
Por cada valor de carga medir la indicación del instrumento.
Carga
I exc
(A)
I
(A)
V
(V)
P
(W)
cosϕ
L1
L2
L3
……
P
cosϕ =
√3 V I
DE LORENZO
Sistemas para la
formación técnica
85
DL 1026A
B) Característica exterior
Sucesión de las maniobras.
Después de haber realizado el circuito a rayas, efectuar las siguientes maniobras :
1
Repetir las operaciones indicadas en los puntos 1 - 3 de la prueba A.
2a
Característica en cosϕ = 1.
Llevar el conmutador solo de la carga R en la posición "1" (2, 3, ……) y por cada
posición relevar las indicaciones de los instrumentos.
2b
Característica en cosϕ = 0,8 retraso.
Llevar contemporáneamente los conmutadores R y L para realizar el cosϕ = 0.8 y por
cada posición relevar las indicaciones de los instrumentos.
I exc
(A)
Carga
I
(A)
R1
R2
R3
……
RL1
RL2
RL3
……
P
cosϕ =
DE LORENZO
Sistemas para la
formación técnica
86
√3 V I
V
(V)
P
(W)
cosϕ
DL 1026A
PRUEBA
PRACTICA
Nº 6
Relieve de las caracteristicas de regulación
La finalidad de esta prueba es la relevar las características de regulación del alternador en
cosϕ = 1 y en cosϕ = 0,8 retraso.
El esquema eléctrico y el topográfico son idénticos a los de la prueba práctica Nº 5.
Sucesión de las maniobras.
1 Repetir las operaciones del punto 1 al 3 de la prueba práctica Nº 5.
2 Característica en cosϕ = 1.
Llevar el conmutador de la carga R de la posición "0" en la posición "1" (2, 3, ……).
Por cada posición, después de haber regulado la tensión de salida hasta obtener el valor
nominal mediante la manivela de excitación, relevar las indicaciones de los instrumentos.
3 Característica en cosϕ = 0,8 retraso.
Regular la carga con cosϕ = 0.8 regulando los conmutadores sobre los modulos de carga
R y L y por cada posición relevar las indicaciones de los instrumentos.
5 Parar el motor abriendo el interruptor.
Carga
I exc
(A)
I
(A)
V
(V)
P
(W)
cosϕ
R1
R2
R3
……
RL1
RL2
RL3
……
P
Cosϕ =
√3 V I
DE LORENZO
Sistemas para la
formación técnica
87
DL 1026A
Página blanca
DE LORENZO
Sistemas para la
formación técnica
88
DL 1026A
PRUEBA
PRACTICA
Nº
7
Paralelo del alternador con la red trifásica
La finalidad de esta prueba es la de realizar el paralelo del alternador con la red trifásica y
de comprobar el intercambio de las potencias P y Q.
PROTECCION
SOBRE
VELOCIDAD
SALIDA
TRIFASICA FIJA
SALIDA CC VARIABLE
SALIDA CC
VARIABLE (Excitación)
K1
Plancha de paralelo
V
Reóstato de arranque
400V
✱
✱
Wb
✱
A1
Wa
2.5A
2A - 400V
✱
Reóstato de excitación
2A - 400V
Frecuencia de red
Transductor
óptico
K2
+
-
A2
rpm
K1
K2
0.6A
Medidor de velocidad
DE LORENZO
Sistemas para la
formación técnica
89
DL 1026A
Sucesión de las maniobras.
Después de haber realizado el circuito a rayas, efectuar las siguientes maniobras:
1 Preparar los mandos de los módulos:
SALIDA CC VARIABLE:
(Excitación)
Interruptor abierto.
Convertidor girado completamente en
sentido antihorario.
SALIDA FIJA TRIFASICA:
Interruptor abierto.
SALIDA CC VARIABLE:
Salida a 220V aprox.
SALIDA CC VARIABLE:
(Excitación)
Interruptor abierto.
PLANCHA DE PARALELO:
Interruptor abierto.
2 Cerrar el interruptor en el módulo trifásico fijo y controlar el valor de la tensión de red.
Cerrar el interruptor de la salida cc variable y regular la manivela de modo que la tensión
de salida del alternador esté cerca del valor de red.
Regular la velocidad de manera que el grupo funcione a una velocidad cerca de la
nominal.
Después controlar la frecuencia de red.
Regular la excitación del alternador en manera que la tensión de salida sea igual a la de
la red.
3 Observar las bombillas H1 - H2 - H3; notaremos que estas se encienden y se apagan con
una sucesión en el tiempo que da la impresión de una rotación de luces.
Convertir esta rotación en lo más lenta posible actuando ligeramente sobre la excitación
del motor mediante la manivela del réostato de excitación.
4 Realizar el paralelo del alternador con la red cerrando el interruptor (posición "on") en la
"plancha de paralelo" en el instante en el que la bombilla H1 está apagada y las H2 y H3
presentan la misma intensidad luminosa.
5 Si las operaciones de paralelo se han realizado correctamente, el alternador hará
perfectamente de equilibrio entre la red y los instrumentos situados entre alternador y red
evidenciando que no existe intercambio de corriente y potencia.
DE LORENZO
Sistemas para la
formación técnica
90
DL 1026A
6 Comprobación del intercambio de potencia activa entre alternador y red.
6.a. Aumentar lentamente la excitación del motor de arrastre "intentando" aumentar la
velocidad de rotación del grupo.
Se notará que la velocidad permanece constante mientras que la potencia activa
resulta positiva fluye del alternador hacia la red.
6.b. Disminuir, a continuación, la excitación del motor de arrastre intentando reducir la
velocidad de rotación del grupo.
Se notará que la velocidad permanece constante mientras que la potencia erogada
disminuirá hasta anularse como en el momento del paralelo.
6.c. Disminuyendo aún la excitación del motor de arrastre se notará un nuevo
intercambio de la potencia activa desde la red hacia el alternador por lo que el
alternador se encuentra ahora funcionando como motor sincrónico.
7 Comprobación del intercambio de potencia reactiva entre alternador y red.
Volver a asumir las posiciones de paralelo, anulando corriente y potencia entre red y
alternador actuando sobre la excitación del motor de arrastre.
Accionar ahora lentamente de manera de aumentar o disminuir la excitación del
alternador.
Comprobar que la tensión de salida no cambie. En caso contrario un nuevo intercambio
de potencia reactiva nacerá entre el alternador y red
8 Abrir el interruptor para parar el grupo
DE LORENZO
Sistemas para la
formación técnica
91
DL 1026A
Página blanca
DE LORENZO
Sistemas para la
formación técnica
92
DL 1026A
PRUEBA
PRACTICA
Nº 8
La finalidad de esta prueba es la de relevar la curva en "V" del alternador funcionando como
motor sincrónico en vacío.
El esquema eléctrico y el topográfico son los mismos de la anterior prueba Nº 7.
Sucesión de las maniobras:
1 Realizar el paralelo del alternador con la red efectuando las maniobras descritas en los
puntos 1 - 2 - 3 - 4 - 5 de la prueba Nº 7.
2 Con el paralelo realizado, abrir el interruptor de la salida cc variable. El motor de arrastre
se desconectará y será arrastrado por el alternador que ha pasado automáticamente a
funcionar como motor sincrónico.
3 Aumentar la excitación de la máquina sincrónica mediante la manivela de manera que
absorba el motor una corriente de aprox. el 10 - 20 % superior al valor nominal.
Relevar las indicaciones de los instrumentos.
4 Reducir progresivamente la excitación y relevar las indicaciones de los instrumentos.
Se notará que al disminuir la corriente de excitación, también se reduce la corriente
absorbida hasta alcanzar un valor mínimo, para a continuación volver a aumentar,
determinando de esta forma la típica forma en "V" del diagrama I = f(i).
5 Parar el grupo.
Nota : Conviene realizar gradualmente las erogaciones de la corriente de excitación para
evitar que se reduzca excesivamente su valor con el consiguiente debilitamiento del
par motriz y posible peligro de que "pierda el paso" la máquina.
DE LORENZO
Sistemas para la
formación técnica
93
DL 1026A
Tabla de relieves
Po ≅ 0
V = …… (V)
Iexc
(A)
Iabs
(A)
Pabs
(W)
Notas
sobre
excitación
Sub
excitación
DE LORENZO
Sistemas para la
formación técnica
94
© 1992 - 2000 DE LORENZO - Printed in Italy - All Rights Reserved
DE LORENZO S.R.L.
V. le Romagna, 20 - 20089 Rozzano (MI)
Tel. ++39 02 8254551/2/3 - Telefax ++39 02 8255181
E-mail: [email protected]
Web site: www.delorenzogroup.com