Geometría del espacio Práctica 1

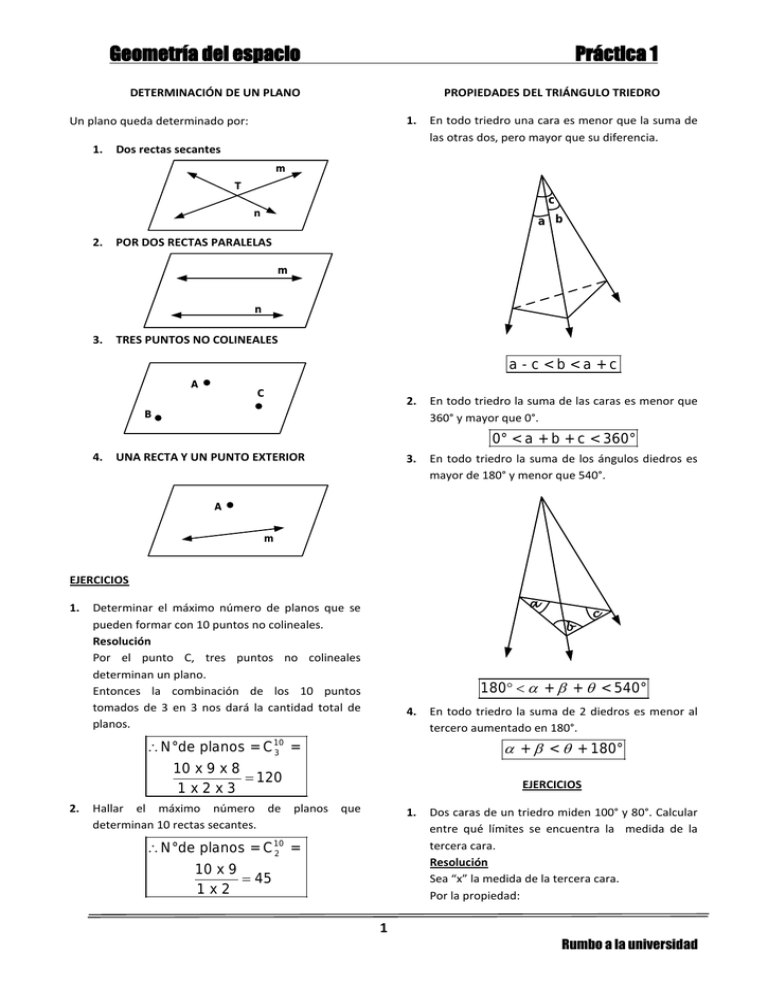
Geometría del espacio
Práctica 1
DETERMINACIÓN DE UN PLANO
PROPIEDADES DEL TRIÁNGULO TRIEDRO
1.
Un plano queda determinado por:
1.
Dos rectas secantes
En todo triedro una cara es menor que la suma de
las otras dos, pero mayor que su diferencia.
m
T
c
n
2.
a b
POR DOS RECTAS PARALELAS
m
n
3.
TRES PUNTOS NO COLINEALES
a-c<b<a+c
A
C
2.
B
En todo triedro la suma de las caras es menor que
360° y mayor que 0°.
0° < a + b + c < 360°
4.
UNA RECTA Y UN PUNTO EXTERIOR
3.
En todo triedro la suma de los ángulos diedros es
mayor de 180° y menor que 540°.
A
m
EJERCICIOS
1.
a
Determinar el máximo número de planos que se
pueden formar con 10 puntos no colineales.
Resolución
Por el punto C, tres puntos no colineales
determinan un plano.
Entonces la combinación de los 10 puntos
tomados de 3 en 3 nos dará la cantidad total de
planos.
b
180° < α + β + θ < 540°
4.
∴ N°de planos = C10
3 =
En todo triedro la suma de 2 diedros es menor al
tercero aumentado en 180°.
α + β < θ + 180°
10 x 9 x 8
= 120
1x2x3
2.
c
EJERCICIOS
Hallar el máximo número de planos que
determinan 10 rectas secantes.
1.
∴ N°de planos = C10
2 =
10 x 9
= 45
1x2
1
Dos caras de un triedro miden 100° y 80°. Calcular
entre qué límites se encuentra la medida de la
tercera cara.
Resolución
Sea “x” la medida de la tercera cara.
Por la propiedad:
Rumbo a la universidad
Geometría del espacio
Práctica 1
9.
0° < a + b + c < 360°
X + 100° + 80° < 360°
X < 180° …. (I)
Por la segunda propiedad:
10.
a-c<b<a+c
2.
3.
100° - 80° < x
20° < x … (II)
De (I) y (II)
20° < x < 180°
Respuesta: la medida varía entre 20° y 180°
Dos caras de un triedro miden 110° y 120°.
Calcular entre qué límites se encuentra la medida
de la tercera cara
Respuesta: ____________
En un triedro O – ABC, los diedros
y
miden
160°. Calcular entre qué límites se encuentra la
medida del diedro
Resolución
Por la CUARTA propiedad:
11.
12.
13.
14.
α + β < θ + 180°
160° + 160° +
+ 180°
140° <
… (I)
Por la TERCERA propiedad
15. La altura de un tetraedro regular mide
Halle la medida de su arista.
Respuesta: ____________
16. Un poliedro convexo, está formado por 10
triángulos, 20 cuadriláteros y 30 pentágonos. Halle
el número de aristas.
Respuesta: ____________
17. Hallar el máximo número de planos determinados
por 20 puntos no colineales y 19 rectas secantes.
a) 1835 b) 1538 c) 1583 d) 1385
e) 1450
18. ¿Cuántos planos como máximo se pueden
determinar con 10 puntos y 8 rectas secantes.
a) 228 b) 282 c) 200 d) 220 e) 250
19. Un poliedro convexo, se sabe que está
conformado por 4 triángulos, 4 cuadriláteros y 2
hexágonos. Halle la diferencia entre el número de
aristas y vértices.
Respuesta: ____________
20. Halle la altura de un tetraedro regular de 1 cm de
arista.
Respuesta: ____________
21. Halle la medida de la diagonal de un octaedro
regular que tiene 2 cm de lado.
Respuesta: ____________
22. Halle la distancia entre los baricentros de dos caras
de un tetraedro regular de 12 cm de arista
Respuesta: ____________
180° < α + β + θ < 540°
4.
5.
6.
7.
8.
En un triedro O – ABC, los diedros
y
miden
130°. Calcular entre qué límites se encuentra la
medida del diedro
Respuesta: ____________
Un poliedro convexo, está formado por 6
triángulos, 8 cuadrados y 6 pentágonos. Halle su
número de vértices.
Respuesta: ____________
Un poliedro convexo, está formado por 15
triángulos, 3 cuadrados y 3 pentágonos. Halle el
número de aristas.
Respuesta: ____________
Halle la altura de un tetraedro regular que tiene 12
m de arista.
Respuesta: ____________
Dos caras de un triedro miden 100° y 130°.
Calcular entre qué límites se encuentra la medida
de la tercera cara.
Respuesta: ____________
Halle la altura de un tetraedro regular que tiene 3
cm de arista.
Respuesta: ____________
160° + 160° +
< 540°
< 220° … (II)
De (I) y (II)
140° <
< 220°
Respuesta: la medida varía entre 140° y 220°
Halle la altura de un tetraedro regular que tiene 6
cm de arista.
Respuesta: ____________
Halle la medida de la diagonal de un cubo de 4 cm.
De arista.
Respuesta: ____________
Halle el máximo número de planos determinados
por 12 puntos no colineales.
Respuesta: ____________
Halle el máximo número de planos determinados
por 16 rectas secantes.
Respuesta: ____________
En un triedro O – ABC, los diedros
y
miden
120° y 100° respectivamente. Calcular entre qué
límites varía la medida del diedro
Respuesta: ____________
2
Rumbo a la universidad
Geometría del espacio
Práctica 1
23. Halle la distancia entre los baricentros de dos caras
24.
25.
26.
27.
28.
29.
30.
31.
32.
de un tetraedro regular de
m de altura.
Respuesta: ____________
Un poliedro convexo está formado por 40
triángulos, 20 cuadriláteros, 60 pentágonos.
Calcular el número de vértices..
Respuesta: ____________
Calcular la relación entre la suma de los ángulos de
la cara de un octaedro regular y un icosaedro
regular.
Respuesta: ____________
Uno de los ángulos diedros complementarios
aumentado en 27° es igual al otro. ¿Cuánto mide
el ángulo mayor?
Respuesta: ____________
Uno de los ángulos diedros suplementarios es 0,8
del otro. ¿Cuánto mide el ángulo diedro mayor?
Respuesta: ____________
¿Cuál es la suma de ángulos de todas las caras de
un dodecaedro?
Respuesta: ____________
Calcular el área total de un cubo cuya suma de sus
aristas es de 96 cm.
Respuesta: ____________
La diagonal de una cara de un cubo mide 18 cm.
Calcular su área total.
Respuesta: ____________
Calcular el área total de un cubo cuya diagonal
mide 18 dm.
Respuesta: ____________
Calcular la diagonal de una cara de un cubo cuya
Respuesta: ____________
36. Expresar el área total de un cubo en función de su
diagonal.
Respuesta: A ST = 2D2
37. Expresar el VOLUMEN de un cubo en función de su
diagonal.
Respuesta: V =
D2 3
9
38. Hallar el área del TRIÁNGULO sombreado si la
arista del cubo es
5 2m
2
área total es 675 cm .
Respuesta: ____________
33. Calcular la diagonal de un cubo cuya área total es
Respuesta:
39. Calcular el número total de diagonales que tiene
un icosaedro regular.
Resolución
Realizamos todas las combinaciones posibles entre
los vértices, tomados de dos en dos, y restamos
todas las diagonales de las caras, así como todas
las aristas.
• El icosaedro regular tiene:
V = 12 vértices.
A = 30 aristas.
• TOTAL DE DIAGONALES:
2
200 m .
Respuesta: ____________
34. Calcular el área total de un exaedro regular,
sabiendo que la distancia de uno de sus vértices al
centro de una cara opuesta es de 4m.
Respuesta: ____________
35. Hallar el área del rectángulo sombreado si el área
total del cubo es
25 3 m2
72m2
CV2 - A = C12
2 - 30 =
66 - 30 = 36
Respuesta: 36 diagonales.
40. La arista de un cubo es de 6 cm. Calcular la
distancia de un vértice a la diagonal.
3
Rumbo a la universidad
Geometría del espacio
Práctica 1
b) El APOTEMA de un polígono regular es la
distancia del centro del polígono al punto
medio de uno de sus lados. ( )
c) El poliedro regular que tiene veinte
vértices y treinta aristas se llama
DODECAEDRO. ( )
d) Entre los poliedros regulares, el que es un
PRISMA se llama CUBO y el que es una
PIRÁMIDE se llama TETRAEDRO. ( )
e) La diferencia entre el número de ARISTAS
de un DODECAEDRO y el número de
(
ARISTAS de un ICOSAEDRO es CERO
)
47. ¿Cuántos planos como máximo se determinan con
40 puntos en el espacio?
Resolución
Un plano es determinado por tres puntos.
Por lo tanto, los 40 puntos, debemos combinarlos
de tres en tres, usando números combinatorios.
x
a = 6 cm
Respuesta: ____________
41. Calcular el número total de diagonales que tiene
un dodecaedro regular.
Respuesta: ____________
42. Si se unen los centros de las caras de un exaedro
se obtiene un:
a) Tetraedro
b) cubo
c) Octaedro
d) Dodecaedro
e) Icosaedro
43.
C340 =
=
40!
=
3! ( 40 − 3 ) !
40!
38.39.40
=
3! ( 37 ) !
1.2.3.
= 9 880 planos
A
Ca
lc
ul
ar
la
di
ag
48. Hallar el máximo número de planos que se
determinan con 18 puntos no colineales y 24
rectas no coplanarias.
Resolución
Con 18 puntos:
on
al
D
M
a = 4 cm
C18
3 = 816
C
Con 24 rectas:
Respuesta: ____________
44. La suma de las longitudes de todas las aristas de
un octaedro regular es de 288 cm. Hallar la
longitud de una de las diagonales.
C24
2 = 276
Pero en un plano también se determina por
un punto y una recta, entonces:
Con 18 puntos y 24 rectas: 18.24 = 432
Respuesta: 24 2 cm
45. ¿Cuál es la medida de la diagonal (d) de una cara
de un cubo y de la diagonal (D) del cubo, si su área
Luego:
N° de planos = 816 + 276 + 432 = 1524
2
es de 294 cm ?
Respuesta: 1524 planos.
Respuestas: d = 7 2 cm, D = 7 3 cm
49. Hallar el máximo número de planos que se
determinan con 9 puntos no colineales y 12 rectas
no coplanarias.
Respuesta: ____________
46. Escriba verdadero (V) o falso (F) según
corresponda:
a) Los POLIEDROS se clasifican en prismas y
pirámides. ( )
4
Rumbo a la universidad