ECUACIONES LINEALES Las ecuaciones lineales pueden tomar

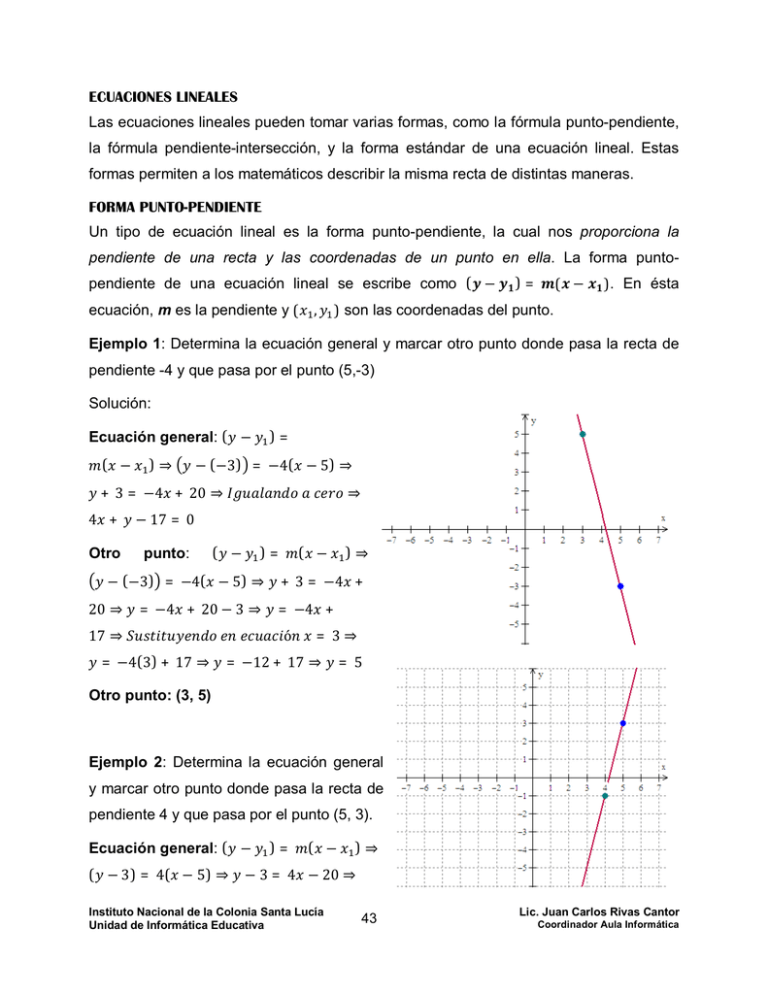
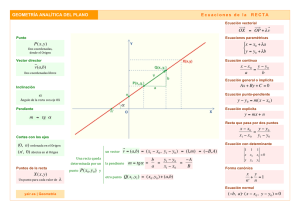
ECUACIONES LINEALES
Las ecuaciones lineales pueden tomar varias formas, como la fórmula punto-pendiente,
la fórmula pendiente-intersección, y la forma estándar de una ecuación lineal. Estas
formas permiten a los matemáticos describir la misma recta de distintas maneras.
FORMA PUNTO-PENDIENTE
Un tipo de ecuación lineal es la forma punto-pendiente, la cual nos proporciona la
pendiente de una recta y las coordenadas de un punto en ella. La forma puntopendiente de una ecuación lineal se escribe como ( −
ecuación, m es la pendiente y ( ,
)=
( −
). En ésta
) son las coordenadas del punto.
Ejemplo 1: Determina la ecuación general y marcar otro punto donde pasa la recta de
pendiente -4 y que pasa por el punto (5,-3)
Solución:
Ecuación general: ( −
( −
)⇒
)=
− (−3) = −4( − 5) ⇒
+ 3 = −4 + 20 ⇒
4 +
− 17 = 0
Otro
punto:
( −
)=
− (−3) = −4( − 5) ⇒
20 ⇒
= −4 + 20 − 3 ⇒
17 ⇒
= −4(3) + 17 ⇒
⇒
( −
)⇒
+ 3 = −4 +
= −4 +
ó =3⇒
= −12 + 17 ⇒
=5
Otro punto: (3, 5)
Ejemplo 2: Determina la ecuación general
y marcar otro punto donde pasa la recta de
pendiente 4 y que pasa por el punto (5, 3).
Ecuación general: ( −
( − 3) = 4( − 5) ⇒
)=
( −
)⇒
− 3 = 4 − 20 ⇒
Instituto Nacional de la Colonia Santa Lucía
Unidad de Informática Educativa
43
Lic. Juan Carlos Rivas Cantor
Coordinador Aula Informática
⇒4 +
Otro punto: ( −
20 + 3 ⇒
17 ⇒
)=
+ 17 = 0
( −
) ⇒ ( − 3) = 4( − 5) ⇒
= 4 − 17 ⇒
ó =4⇒
− 3 = 4 − 20 ⇒
= 4(4) − 17 ⇒
=4 −
= 16 −
= −1 Otro punto: (4, -1)
Ejercicio de aplicación: Una recta pasa por el
punto (3,-1) y tiene pendiente 2. Marca en el
plano otro punto por el que pase la recta.
Además, escribe las coordenadas de dicho punto.
Otro punto: ( −
2( − 3) ⇒
)=
( −
+1 =2 −6 ⇒
=2 −7 ⇒
= 2(0) − 7 ⇒
) ⇒ ( − (−1)) =
=2 −6−1⇒
ó =0⇒
= −7
Otro punto: (0, -7)
Instituto Nacional de la Colonia Santa Lucía
Unidad de Informática Educativa
44
Lic. Juan Carlos Rivas Cantor
Coordinador Aula Informática
Ejercicio de aplicación. De las siguientes gráficas, la que corresponde a ( ) = −2 − 1
es
Solución:
( ) = −2 − 1 ⇒
= −2(0) − 1 ⇒
= −1 ⇒ (0, −1)
= −2 − 1 ⇒ 0 = −2 − 1 ⇒ 2 = −1 ⇒
1
1
= − ⇒ (− , 0)
2
2
Resultado: Evaluando los dos puntos encontrados y asignándolo a la grafica la
respuesta correcta seria el literal B.
Instituto Nacional de la Colonia Santa Lucía
Unidad de Informática Educativa
45
Lic. Juan Carlos Rivas Cantor
Coordinador Aula Informática