68.Para el sistema de capacitores mostrado en la figura encuentre

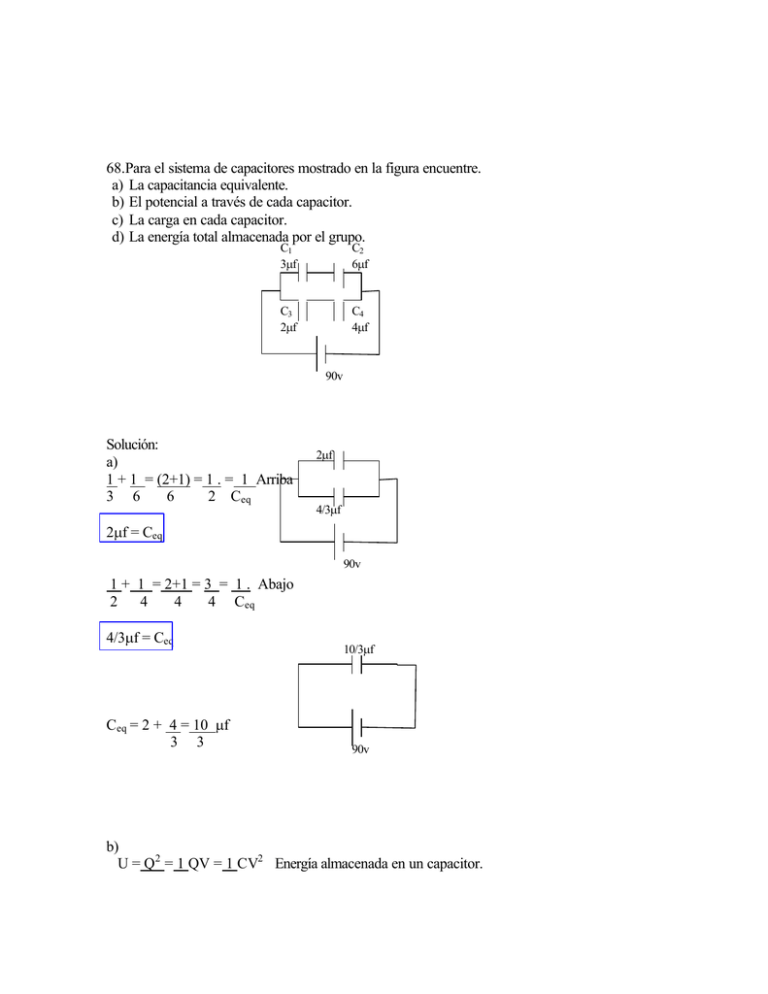
68.Para el sistema de capacitores mostrado en la figura encuentre.
a) La capacitancia equivalente.
b) El potencial a través de cada capacitor.
c) La carga en cada capacitor.
d) La energía total almacenada por el grupo.
C1
3µf
C2
6µf
C3
2µf
C4
4µf
90v
Solución:
a)
1 + 1 = (2+1) = 1 . = 1 Arriba
3 6
6
2 Ceq
2µf
4/3µf
2µf = Ceq
90v
1 + 1 = 2+1 = 3 = 1 . Abajo
2
4
4
4 Ceq
4/3µf = Ceq
Ceq = 2 + 4 = 10 µf
3 3
10/3µf
90v
b)
U = Q2 = 1 QV = 1 CV2 Energía almacenada en un capacitor.
2C
2
2
Cuando son paralelos tienen el mismo voltaje y de ahí sacamos la carga que hay en cada
lado.
2µf
Q = V . Ceq
Q1 = 90V * 2µf
4/3µf
Q1 = 180 µC
Q2 = 90V * 4/3 *10-6
Q2 = 120 µC
Después de tener la carga se sabe que cuando los condensadores que están en serie tienen la
misma carga, entonces la energía potencial es Q2 /2C
Energía potencial en:
C1 : (180 C)2 /2 * 3µf = 5.4*10-3 J
C2 : (180 C)2 /2 * 6µf = 2.7*10-3 J
C3 : (120 C)2 /2 * 2µf = 3.6*10-3 J
C4 : (120 C)2 /2 * 4µf = 1.8*10-3 J
c) La carga en cada capacitor:
La carga ya la calculamos en el punto b) y es igual a:
QC1 = 180µC
QC2 = 180µC
QC3 = 120µC
QC4 = 120µC
e) La energía total almacenada por el grupo:
Ya sabemos que el condensador equivalente es igual a 10/3 µf por lo tanto utilizamos la
formula de la energía. U = 1 CV2 = 1 * 10*10-6 * 902 = 81*10-3 J
2
2 3
6