CAPITULO 3.- Representaciones de Fourier para señales.

CAPITULO 3.- Representaciones
de Fourier para señales.
3.1 Introducción.
3.2 Señales periódicas en tiempo discreto: la serie de Fourier
en tiempo discreto.
3.3 Señales periódicas en tiempo continuo: la serie de Fourier.
3.4 Señales no periódicas en tiempo discreto: la transformada
de Fourier en tiempo discreto
3.5 Señales no periódicas en tiempo continuo: la transformada
de Fourier
3.3.6 Propiedades de las representaciones de Fourier
3.1 Introducción.
Análisis de Fourier :
Representación de señales utilizando senoides complejas
Senoides complejas y respuesta en frecuencia de sistemas LTI
x(t ) = e jωt
senoidal compleja
y (t ) = H ( jω )e jωt
y (t ) = H ( jω ) e
∞
; H ( jω ) = ∫ h(τ )e − jωτ dτ ⇒ resp. en frecuencia
−∞
j (ωt + arg{H ( jω )})
x[n] = e jΩn
y[n] = H (e jΩ )e jΩn
y[n] = H (e ) e (
jΩ
; H (e jΩ ) =
{
j Ωn + arg H ( e jΩ )
})
∑ h[k ](e )
∞
jΩ − k
k = −∞
1
Ejemplo
Circuito RC : Respuesta en frecuencia
1
h(t ) =
1 − RC t
e
u (t ) , ∀t ≥ 0
RC
1
1
RC =
H ( jω ) =
1
jωRC + 1
jω +
RC
ψ (t )
H ( jω ) =
1
RC
ω + 1 RC
2
(
)
2
arg{H ( jω )} = − arctan (ωRC )
Figure 3.4 (p. 198)
(a) General eigenfunction Ψ(t) or Ψ[n] and eigenvalue λ.
(b) Complex sinusoidal eigenfunction ejωt and eigenvalue
H(jω).
(c) Complex sinusoidal eigenfunction ejΩn and eigenvalue
H(ejΩ).
λψ (t )
ψ [n]
λψ [n]
Función característica de H
Función propia
j ωt
ψ (t ) = e
Vector característico de A
ek
M
x(t ) = ∑ ak e jωk t
k =1
Problema de valores
característicos
H {ψ (t )} = λψ (t )
Valor característico
Valor propio
H ( jω ) = λ
Valor característico
Ae k = λk e k
λk
M
y (t ) = ∑ ak H ( yωk )e jωk t
k =1
2
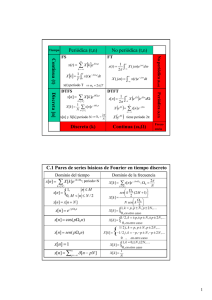
Representaciones de Fourier para cuatro clases de señales
Propiedad
de tiempo
Periódica
No periódica
Continua
Serie de Fourier
(FS)
Transformada de
Fourier (FT)
Discreta
Serie de Fourier en Transformada de
tiempo discreto
Fourier en tiempo
(DTFS)
discreto (DTFT)
Señales periódicas: representaciones mediante las series
de Fourier
DTFS : Periodo fundamental de x[n] : N
FS : Periodo fundamental de x(t) : T
⇒ Ω 0 = 2π N
⇒ ω0 = 2π T
3
3.2 Señales periódicas en tiempo discreto:
la serie de Fourier en tiempo discreto (DTFS).
∑ X [k ]e
x[n] =
jkΩ 0 n
X [k ] =
k= N
1
N
∑ x[n]e
− jkΩ 0 n
n= N
DTFS :Ω 0
x[ n] ↔ X [k ]
Ω0 =
2π
N
X[k],x[n] : par DTFS
N =−
N = 0,1,..., N − 1
N
N
,..., − 1
2
2
Representación en el dominio de la frecuencia
Espectro de magnitud de x[n]
arg{X [k ]} Espectro de fase de x[n]
X [k ]
X [k ]
X [k + N ] =
1
N
∑ x[n]e
− j ( k + N )Ω0n
=
n= N
1
N
∑ x[n]e
− jNΩ 0 n − jkΩ 0 n
e
=
n= N
1
N
∑ x[n]e
− jkΩ 0 n
= X [k ]
n= N
X[k] y x[n] : evaluar en computadora (únicas)
Problema 3.48
Utilice la definición de los coeficientes de la DTFS para
evaluar la representación DTFS para la señal :
π⎞
⎛ 6π
x[n] = cos⎜
n+ ⎟
3⎠
⎝ 17
x[n] =
2π
N = 17, Ω 0 =
17
X [k ] =
∑ X [k ]e
jkΩ 0 n
k= N
1
N
8
∑ x[n]e
− jkΩ 0 n
k = −8
⎛ 6π π ⎞
⎛ 6π π ⎞
π
π
2π
2π
1 ⎛ j ⎜ n + ⎟ − j ⎜ n + ⎟ ⎞ ⎡ 1 j ⎤ j (3) n ⎡ 1 − j ⎤ j ( −3) 17 n
x[n] = ⎜ e ⎝ 17 3 ⎠ + e ⎝ 17 3 ⎠ ⎟ = ⎢ e 3 ⎥ e 17 + ⎢ e 3 ⎥ e
⎟ ⎣2
2 ⎜⎝
⎦
⎣2
⎦
⎠
π
1 j3
e
k =3
2
π
1 −j3
e
k = −3
2
0 otros k ,−8 ≤ k ≤ 8
{
X [k ] =
4
Problema 3.2
Encontrar la representación en el dominio de la frecuencia de
la señal descrita en la figura
x[-n]=-x[n] : simetría impar ;
X [k ] =
N=5
, Ω0=2π/5
{
1 2
1
x[n]e − jk 2π n 5 = x[−2]e jk 4π 5 + x[ −1]e jk 2π 5 + x[0]e j 0 + x[1]e − jk 2π 5 + x[2]e − jk 4π
∑
5 n = −2
5
5
}
1 ⎧1
1
⎫ 1
X [k ] = ⎨ e jk 2π 5 + 1 − e − jk 2π 5 ⎬ = {1 + j sen(k 2π 5)}
5 ⎩2
2
⎭ 5
1
sen(4π 5)
1
sen( 2π 5)
X [ − 2] = − j
= 0,232e − j 0,531 ; X [−1] = − j
= 0,276e − j 0, 760
5
5
5
5
1
X [0] = = 0,2e j 0
5
sen(2π 5)
sen(4π 5)
1
1
X [1] = + j
= 0,276e j 0 ,760 ; X [ 2] = + j
= 0,232e j 0,531
5
5
5
5
Problema 3.2 (cont.)
X [−2] = 0,232e − j 0,531 ;
X [1] = 0,276e j 0, 760
;
X [−1] = 0,276e − j 0,760
;
X [0] = 0,2e j 0
X [2] = 0,232e j 0,531
5
Ejemplo 3.5
(Inversa de DTFS)
Determine la señal en el dominio del tiempo x[n] a partir
de los coeficientes DTFS descritos en la figura :
N=9 ,
Ω0=2π/9
x[n] =
4
∑ X [k ]e
jk 2πn 9
= e j 2π 3e − j 6πn 9 + 2e jπ 3e − j 4πn 9 − 1 + 2e − jπ 3e j 4πn 9 + e − j 2π 3e j 6πn 9
k = −4
x[n] = 2 cos(6πn 9 − 2π 3) + 4 cos(4πn 9 − π 3) − 1
3.3 Señales periódicas en tiempo continuo:
la serie de Fourier
a) FS exponencial
FS : Periodo fundamental de x(t) : T ⇒ ω0 = 2π T
FS exponencial
x(t ) =
∞
∑ X [k ]e
jkω0t
;
X [k ] =
k = −∞
FS ;ω0
x(t ) ↔ X [k ]
X [k ]
X [k ]
arg{X [k ]}
1
T
∫
T
0
x(t )e − jkω0t dt ;
X[k],x[n] : par FS
Representación en el dominio de la frecuencia
Espectro de magnitud de x[n]
Espectro de fase de x[n]
6
Ejemplo 3.9
(Cálculo directo de coeficientes FS)
Determine los coeficientes FS para la señal x(t) descrita en
la figura :
ω0 = 2π T = 2π 2 = π
1 2 − 2t − jkπ t
1 2
−1
e e
dt = ∫ e −( 2+ jkπ ) t dt =
e −( 2+ jkπ )t
∫
0
0
2
2
2(2 + jkπ )
1
X [k ] =
(1 − e − 4 e − jk 2π )
4 + jk 2π )
X [k ] =
X [k ] =
|
2
0
1 − e−4
4 + jk 2π )
Ejemplo 3.12
(Inversa FS)
Encuentre la señal en el dominio del tiempo x(t) correspondiente
k
a los coeficientes FS :
X [k ] = 1
e jkπ 20
2
Suponiendo que el periodo fundamental es T=2 ⇒ ω0 = 2π T = π
( )
∞
( 2) e
jkπ 20
( 2) e
jkπ 20
x(t ) = ∑ 1
k =0
∞
x(t ) = ∑ 1
k =0
k
k
−∞
( 2)
e jkπ 20 e jkπt
( 2) e
− jlπ 20 − jlπt
e jkπt + ∑ 1
−k
k = −1
∞
e jkπt + ∑ 1
l =1
l
1
1
+
j (πt +π 20 )
1 − (1 / 2)e
1 − (1 / 2)e − j (πt +π
3
x(t ) =
5 − 4 cos(π t + π / 20)
x(t ) =
e
20 )
−1
7
Ejemplo 3.13
(FS para una onda cuadrada)
Determine la representación FS de la onda cuadrada x(t)
descrita en la figura :
X [k ] =
1 T /2
1 T0
− 1 − jkω0t
x(t )e − jkω0t dt = ∫ e − jkω0t dt =
e
∫
T −T / 2
T −T0
Tjkω0
X [k ] =
2 ⎛ e jkω0T0 − e − jkω0T0
⎜
2j
Tkω0 ⎜⎝
X [k ] =
2 sen(kω0T0 )
Tkω0
|
T0
−T0
, k≠0
⎞ 2sen(kω0T0 )
⎟⎟ =
, k ≠0
Tkω0
⎠
1 T0
2T
2sen(kω0T0 ) 2T0
;
lim
k = 0 ⇒ X [k ] = ∫ dt = 0
=
k →0
T −T0
T
Tkω0
T
ω0 =
2π
T
⇒
X [k ] =
Ejemplo 3.13 (cont.)
2sen(k 2πT0 / T ) 2T0
⎛ 2T ⎞
senc⎜ k 0 ⎟
=
k 2π
T
⎝ T ⎠
X [k ], − 50 ≤ k ≤ 50
T0/T=1/4
La energía en la representación
FS esta distribuida en un ancho
intervalo de frecuencias
El primer cruce por cero :
T0/T=1/16
T0/T=1/4
k=2
T0/T=1/16
k=8
T0/T=1/64
k=32
Al decrecer T0/T la energía en
T0/T=1/64
cada periodo de la señal onda
cuadrada se concentra alrededor
de un estrecho intervalo de tiempo.
8
3.3
Con bastante frecuencia en el análisis de Fourier aparece la forma
funcional :
senc(u ) =
sen(π u )
πu
senc(0) = 1
senc(ku ) = 0 , k ≠ 0
El máximo de la función es la unidad en u=0
El cruce por cero ocurre en los valores enteros de u
Lóbulo principal de la función senc : parte de la función entre los
cruces por cero en u=+1 y u=-1
Lóbulos laterales : resto de lóbulos
3.3 Señales periódicas en tiempo continuo:
la serie de Fourier
b) FS trigonométrica
X [−k ] = X [k ]
x(t ) =
∞
∞
k = −∞
m =1
(
)
∑ X [k ]e jkω0t = X [0] + ∑ X [m]e jmω0t + X [−m]e − jmω0t =
∞
∞
e jmω0t + e − jmω0t
=X [0] + ∑ 2 X [m] cos(mω0t )
2
m =1
B[k ] = 2 X [k ], k ≠ 0, entonces
x(t ) = X [0] + ∑ 2 X [m]
m =1
si B[0] = X [0] y
∞
x(t ) = ∑ B[k ] cos(kω0t )
k =0
9
3.3 Señales periódicas en tiempo continuo:
la serie de Fourier
b) FS trigonométrica
∞
x(t ) = B[0] + ∑ { B[k ]cos(kω0t ) + A[k ]sen(kω0t )}
k =1
1 T
x(t )dt
T ∫0
2 T
k ≠ 0, B[k ] = ∫ x(t ) cos(kω0t )dt =
T 0
2 T
A[k ] = ∫ x(t ) sen(kω0t )dt =
T 0
B[0] =
exponencial : x(t ) =
∞
∑ X [k ]e
jkω0t
;
X [k ] =
k = −∞
X [k ] + X [− k ]
j ( X [k ] − X [− k ])
1
T
∫
T
0
x(t )e − jkω0t dt ;
Ejemplo 3.13 (FS trigonométrica para una onda cuadrada)
ω0 = 2π T
T
1 T
1 ⎡ T0
2T
x
(
t
)
dt
1
dt
1dt ⎤ = 0
=
+
∫
∫
∫
⎢
⎥
−
0
0
T
T
0
⎦ T
T
T⎣
2 T
2 sen(k 2πT0 / T )
k ≠ 0, B[k ] = ∫ x(t ) cos(kω0t )dt =
T 0
kπ
2 T
A[k ] = ∫ x(t ) sen(kω0t )dt = 0
T 0
B[0] =
∞
j
x(t ) = ∑ B[k ]cos(kω0t ) ; xˆ j (t ) = ∑ B[k ]cos(kω0t )
k =0
k =0
T = 1 ; ω0 = 2π T ; T0 / T = 1 / 4
10
Figure 3.25b-3 (p. 226)
(b) J = 3. (c) J = 7. (d) J = 29.
(e) J = 99.
3.4
Señales no periódicas en tiempo discreto:
La transformada de Fourier en tiempo discreto (DTFT)
De manera intuitiva deduciremos DTFT a partir de DTFS,
describiendo una señal no periódica como el límite de una señal
periódica cuyo periodo N se acerca a infinito.
DTFT
1 π
jΩ
jΩn
(
)
x[n] =
X
e
e
d
Ω
x
[
n
]
↔ X e jΩ
2π ∫−π
( )
( ) ∑ x[n] e
X e jΩ =
∞
− jΩn
Representación en el dominio de la frecuencia
n = −∞
Si x[n] duración infinita, ha de ser absolutamente
sumable para que exista la DTFT :
∞
∑ x[n] < ∞
n = −∞
∞
2
Si x[n] no es absolutamente sumable, pero tiene energia
∑ x[n] < ∞
n = −∞
finita, la DTFT converge en un sentido de error cuadrático
medio, pero no converge puntualmente
La señal escalón unitario u[n] no cumple las condiciones anteriores
11
Ejemplo 3.17
Secuencia exponencial
Encuentre la DTFT de la secuencia x[n]=αnu[n]
( ) ∑ x[n] e
∞
X e jΩ =
− jΩn
n = −∞
( ) ∑α
∞
X e jΩ =
n = −∞
n
( )
si α es real : X e jΩ =
( )
X e jΩ =
(
∞
∞
n =0
n=0
u[ n] e − jΩn = ∑ α n e − jΩn = ∑ αe − jΩ
n
=
1
,
1 − α e − jΩ
α <1
1
1 − α cos Ω + jαsenΩ
1
(1 − α cos Ω ) + α 2 sen 2Ω
2
)
=
1
α + 1 − 2α cos Ω
2
;
par
⎛ αsenΩ ⎞
arg X e jΩ = − arctan⎜
⎟ ; impar
⎝ 1 − α cos Ω ⎠
{ ( )}
Figure 3.29 (p.232)
Ejemplo 3.17 (cont.)
The DTFT of an exponential signal x[n] = (α)nu[n]. (a)
Magnitude spectrum for α = 0.5. (b) Phase spectrum for α = 0.5.
(c) Magnitude spectrum for
α = 0.9. (d) Phase spectrum for α = 0.9.
12
Ejemplo 3.19
Función senc en tiempo discreto
p =π
−π
( )
X e jΩ =
{01,,
π
Ω <W
W < Ω <π
( ) está especificada sólo para :− π < Ω < π
; X e jΩ
1
1
e jΩn |W−W =
sen(Wn), n ≠ 0
πn
2π nj
1
W
n = 0 ⇒ x[0] = lim
sen(Wn) =
n →0 π n
π
x[n] =
1
2π
x[n] =
1
W
⎛ Wn ⎞
sen(Wn) = senc⎜
⎟
πn
π
⎝ π ⎠
W
∫
−W
e jΩ n d Ω =
x[n] =
Ejemplo 3.20
∫ π X (e )e
π
−
jΩ
jΩn
dΩ
DTFT del impulso unitario : δ(t)
( ) ∑ δ [ n] e
∞
X e jΩ =
1
2π
− jΩn
=1
n = −∞
DTFT
δ [ n] ↔ 1
Ejemplo 3.21 Inversa DTFT del espectro impulso unitario : δ(Ω)
( )
X e jΩ = δ ( Ω ) , − π < Ω < π
x[ n] =
1
2π
π
∫ π δ (Ω ) e
−
jΩn
dΩ =
1
2π
1 DTFT
↔ δ [Ω] , − π < Ω < π
2π
utilizando la propiedad de filtrado de
la función impulso
( ) ∑ δ (Ω − k 2π )
X e jΩ =
∞
k = −∞
13
3.5 Señales no periódicas en tiempo continuo :
La transformada de Fourier (FT)
x(t ) =
∞
X ( jω ) = ∫ x(t )e
− j ωt
−∞
dt
1
2π
∫
∞
−∞
X ( jω )e jωt dω
x(t ) ↔ X ( jω )
FT
representación en el dominio de la frecuencia
La convergencia puntual está garantizada en todos los valores de t
excepto en aquellos correspondientes a discontinuidades si x(t)
satisface las CONDICIONES DE DIRICHLET : (para señales
no periódicas)
∞
∫−∞ x(t ) dt < ∞
1.- x(t) es absolutamente integrable.
2.- x(t) tiene un número finito de máximos, mínimos y
discontinuidades locales en todo intervalo finito.
3.- el tamaño de cada discontinuidad es finito.
La función escalón no es absolutamente integrable
Ejemplo 3.25
Pulso rectangular
Considere el pulso rectangular descrito en la figura y definido
1, − T0 ≤ t ≤ T0
como :
Encuentre la FT de x(t)
x(t ) =
{0,
t > T0
El pulso rectangular x(t) es absolutamente integrable, siempre que
∞
T0
−∞
−T0
X ( jω ) = ∫ x(t )e − jωt dω = ∫ e − jωt dω =
ω = 0 ⇒ X ( j 0) = lim
ω →0
X ( jω ) = 2
2
ω
sen(ωT0 )
ω
− 1 − jωt T0
2
|−T0 = sen(ωT0 ), ω ≠ 0
e
jω
ω
sen(ωT0 ) = 2T0
{
; arg{X ( jω )} =
0,
sen(ωT0 )
>0
ω
sen(ωT0 )
<0
π,
ω
⎛ ωT ⎞
X ( jω ) = 2Tsenc⎜ 0 ⎟
⎝ π ⎠
14
Ejemplo 3.25 (cont.)
X ( jω ) = 2
Si To aumenta
señal x(t) se dispersa en el
origen en el dominio t
sen(ωT )
ω
Si π/To disminuye
señal X(jω) se dispersa en el
origen en el dominio ω
Ejemplo 3.27
Impulso unitario
Encuentre la FT de x(t)=δ(t)
X(t) no satisface las condiciones de Dirichlet, a pesar de ello
∞
X ( jω ) = ∫ δ (t )e − jωt dω = 1
−∞
FT
δ (t ) ↔ 1 ; − ∞ < ω < ∞
Ejemplo 3.28
Inversa FT de un espectro impulso
Encuentre la inversa FT de
X ( jω ) = 2πδ (ω )
x(t ) =
1
2π
∫
∞
−∞
2πδ (ω )e jωt dω = 1
FT
1 ↔ 2πδ (ω )
15
3.6 Propiedades de las representaciones de Fourier
3.6.0 Perioricidad
3.6.1 Linealidad
3.6.2 Simetría – Señales reales e imaginarias
3.6.2 Simetría – Pares e impares
3.6.3 Corrimiento en el tiempo
3.6.4 Corrimiento en frecuencia
3.6.4 Escalamiento
3.6.5 Diferenciación e integración, sumatoria y dif.
3.6.6 Convolución y modulación
3.6.7 Filtrado. Modulación en frecuencia
3.6.8 Relación de Parseval
3.6.9 Dualidad
3.6.10 Producto tiempo-ancho de banda
Tabla
Tiempo
No periódica (t,n)
Serie de Fourier
Tranformada de Fourier
x(t ) =
∞
∑ X [k ]e
jkω0t
x(t ) =
k = −∞
1
T
X [k ] =
∫
T
0
x(t )e − jkω0t dt
1
2π
∫
∞
−∞
X ( jω )e jω t dω
∞
X ( jω ) = ∫ x(t )e − jω t dt
−∞
x(t) periodo T ⇒ ω0 = 2π T
x[n] =
∑ X [k ]e
jkΩ 0 n
x[n] =
k= N
X [k ] =
1
N
∑ x[n]e
π
jΩ
2π
N
( )
X e jΩ
jΩ n
−
X e jΩ =
n= N
Discreta (k)
∫ π X (e )e
( ) ∑ x[n] e
− jkΩ 0 n
x[n] y X[k] periodo N ⇒ Ω 0 =
1
2π
∞
dΩ
− jΩ n
n = −∞
tiene periodo 2π
Continua (ω,Ω)
Periódica (k,Ω)
Discreta [n]
Serie Fourier Tiempo Discr. Tranf. Fourier Tiempo Discr.
No periódica (k,ω)
Continua (t)
Periódica (t,n)
Frecuencia
3.6.0 Perioricidad
16
3.6.1 Linealidad
FT
z (t ) = ax(t ) + by (t ) ↔ Z ( jω ) = aX ( jω ) + bY ( jω )
FS ;ω0
z (t ) = ax(t ) + by (t ) ↔ Z [k ] = aX [k ] + bY [k ]
DTFT
z[n] = ax[n] + by[n] ↔ Z (e jΩ ) = aX (e jΩ ) + bY (e jΩ )
DTFS ;Ω 0
z[n] = ax[n] + by[n] ↔ Z [k ] = aX [k ] + bY [k ]
3.6.2 Simetría – Señales reales e imaginarias puras
a) x(t) Real
Representación Forma compleja
FT
X ( jω ) = X ( − jω )
FS
X *[k ] = X [− k ]
DTFT
X * ( e jΩ ) = X ( e − jΩ )
Forma rectangular
Re{X ( jω )} = Re{X (− jω )}
Im{X ( jω )} = − Im{X (− jω )}
Re{X [k ]} = Re{X [− k ]}
Im{X [k ]} = − Im{X [− k ]}
{
} {
}
Im{X (e )} = − Im{X (e )}
Re X (e jΩ ) = Re X (e − jΩ )
jΩ
DTFS
X *[k ] = X [−k ]
− jΩ
Re{X [k ]} = Re{X [− k ]}
Im{X [k ]} = − Im{X [− k ]}
17
3.6.2(cont.) Simetría – Señales reales e imaginarias puras
b) x(t) Imaginaria pura
Representación Forma compleja
FT
X ( jω ) = − X ( − jω )
FS
X *[k ] = − X [−k ]
DTFT
Forma rectangular
Re{X ( jω )} = − Re{X (− jω )}
Im{X ( jω )} = Im{X (− jω )}
Re{X [k ]} = − Re{X [− k ]}
Im{X [k ]} = − Im{X [− k ]}
{
}
{
}
Im{X (e )} = Im{X (−e )}
X * (e jΩ ) = − X (e − jΩ ) Re X (e jΩ ) = − Re X (−e jΩ )
jΩ
DTFS
X *[k ] = − X [−k ]
jΩ
Re{X [k ]} = − Re{X [− k ]}
Im{X [k ]} = Im{X [− k ]}
3.6.2(cont) Simetría – Pares e impares
c) x(t) valores reales y simetría impar ⇒ x* (t ) = x(t ) ; x(−t ) = − x(t )
*
∞
∞
∞
X * ( jω ) = ⎡ ∫ x(t )e − jωt dt ⎤ = ∫ x* (t )e jωt dt = ∫ x(t )e jωt dt =
⎢⎣ −∞
⎥⎦
−∞
−∞
∞
∞
−∞
−∞
= − ∫ x( −t )e − jω ( − t ) dt = ∫ x(τ )e − jτ t dτ = X ( jω )
La única manera de que la condición X*(jω)=X(jω) se cumpla es
que X(jω) sea real.
d) x(t) valores reales y simetría par ⇒ x* (t ) = x(t ) ; x(−t ) = x(t )
*
∞
∞
∞
X * ( jω ) = ⎡ ∫ x(t )e − jωt dt ⎤ = ∫ x* (t )e jωt dt = ∫ x(t )e jωt dt =
⎢⎣ −∞
⎥⎦
−∞
−∞
∞
∞
−∞
−∞
= ∫ x(−t )e − jω ( − t ) dt = − ∫ x(τ )e − jτ t dτ = − X ( jω )
Luego para que X*(jω)=-X(jω) necesariamente X(jω) es imaginario
puro.
18
3.6.3 Corrimiento en el tiempo
FT
x(t − t0 ) ↔ e − jωt0 X ( jω )
x(t − t0 )
FS ;ω0
↔
DTFT
x[n − n0 ]
x[n − n0 ]
e − jkω0t0 X [k ]
e − jΩn0 X (e jΩ )
↔
DTFS ;Ω 0
e − jkΩ0 n0 X [k ]
↔
3.6.4 Corrimiento en frecuencia
FT
jγ t
X ( j (ω − γ ))
e x(t ) ↔
e
e
e
jk 0ω0t
j Γn
x(t )
x[n]
jk 0 Ω 0 n
FS ;ω0
↔
DTFT
↔
DTFS ;Ω 0
x[n] ↔
X [k − k0 ]
X (e j ( Ω − Γ ) )
X [k − k0 ]
19
3.6.4 Escalamiento : TF
FT
x(t ) ↔ X ( jω ) ; z (t ) = x(at )
FT
x(at ) = z (t ) ↔
1 ⎛ ω⎞
X ⎜ j ⎟ = Z ( jω )
a ⎝ a⎠
Reproducir a velocidad más alta (a>1), comprimimos señal de tiempo.
En el dominio de la frecuencia se expande, más agudos.
Ejemplo 3.48 Escalamiento a un pulso rectangular
Considere el pulso rectangular definido como : x(t ) =
(ver ejemplo 3.25)
Su tranformada de Fourier es :
X ( jω ) =
2
ω
{10,,− T ≤tt >≤TT
0
0
0
sen(ωT0 )
Si T0=1. Calcular la Transformada de Fourier de y(t)=x(t/2) .
x(t ) =
{01,,
t <1
t >1
y (t ) =
{10,,
t <2
t >2
⎛ ω ⎞
1
⎟ = 2 X ( j 2ω ) = 2 2 sen(2ω ) = 2 sen(2ω )
Y ( jω ) =
X⎜ j
⎜
⎟
1
1
2ω
ω
2 ⎝ 2⎠
20
Figure 3.71 (p. 301)
Application of the FT scaling property in Example 3.48.
(a) Original time signal. (b) Original FT. (c) Scaled time
signal y(t) = x(t/2). (d) Scaled FT Y(jω) = 2X(j2ω).
3.6.4 Escalamiento : FS
si x(t) tiene periodo fundamental T (ω0),
z(t) tiene periodo fundamental T/a (aω0)
x(t )
x(at ) = z (t )
FS ;ω0
↔
FS ; aω0
↔
X [k ]
Z [k ] = X [k ]
La operación de escalamiento cambia simplemente el
espaciamiento armónico de (ω0) a (a ω0)
21
3.6.4 Escalamiento : DTFT , DTFS
z[n] = x[ pn], ∀p ∈ Z
p > 1 ⇒ perdida de información
;
x z [n] = 0, a menos que
n
∈Z
p
DTFT
x z ( pn) ↔ X z (e jΩ / p )
x z ( pn)
DTFS ; pΩ 0
↔
p X z [k ]
Problema 3.80
Dada la señal de la figura :x z [n] = 0, a menos que
n
∈Z
p
; p=3
jΩ
a) Demostrar que la DTFT de z[n]=xz[pn] es : Z [e jΩ ] = X z [e p ]
b) De la DTFT de w[n] y prop. escalamiento, calcule la DTFT de f[n]
c) Si xz[n] es periódica (N), z[n]=xz[pn] es periódica (N/p) demostrar :
Z [k ] = pX z [k ]
22
Problema 3.80 (cont.)
a) X z [e
b)
jΩ
p
∑ xz [n]e
]=
−j
Ω
n n = pr
p
∞
suma r impar
∑ xz [ pr ]e − jΩr =
=
n = −∞
r = −∞
DTFT
n
n par
{w0[n ,2n] ,impar
1
Z [k ] =
N
N
−1
p
∑ z[n]e
p
1
Z [k ] = p
N
− jknΩ '0
n=0
N
−1
p
∑ x [ pn]e
n =0
DTFT
↔ F (e j 2 Ω ) =
; Ω '0 =
− jknpΩ 0
z
∞
∑ x [ pn]e
n = −∞
− jΩn
z
=Z [e jΩ ]
1
1 − 0 .9 e − j Ω
w[n] = (0.9 ) u[n] ↔ W (e jΩ ) =
f [n] =
c)
∞
1
1 − 0 .9 e − j 2 Ω
2π
= pΩ 0
N
p
l = pn
=
1 N −1
∑ xz [l ]e − jklΩ0
N n =0
Z [k ] = pX z [k ]
=p
Tiempo
No periódica (t,n)
Serie de Fourier
Tranformada de Fourier
x(t ) =
∞
∑ X [k ]e
jkω0t
x(t ) =
k = −∞
1
T
X [k ] =
∫
T
0
x(t )e − jkω0t dt
1
2π
∫
∞
−∞
X ( jω )e jω t dω
∞
X ( jω ) = ∫ x(t )e − jω t dt
−∞
x(t) periodo T ⇒ ω0 = 2π T
x[n] =
∑ X [k ]e
jkΩ 0 n
x[n] =
k= N
X [k ] =
1
N
∑ x[n]e
π
jΩ
2π
N
( )
X e jΩ
jΩ n
−
X e jΩ =
n= N
Discreta (k)
∫ π X (e )e
( ) ∑ x[n] e
− jkΩ 0 n
x[n] y X[k] periodo N ⇒ Ω 0 =
1
2π
∞
dΩ
− jΩ n
n = −∞
tiene periodo 2π
Continua (ω,Ω)
Periódica (k,Ω)
Discreta [n]
Serie Fourier Tiempo Discr. Tranf. Fourier Tiempo Discr.
No periódica (k,ω)
Continua (t)
Periódica (t,n)
Frecuencia
23
3.6.5 Diferenciación e integración, sumatoria y diferencia
Diferenciación en el tiempo
FT: x(t ) =
1
2π
∫
∞
−∞
d
1
x(t ) = jω
dt
2π
X ( jω )e jω t dω ;
∫
∞
−∞
X ( jω )e jω t dω = jω X ( jω )
FT
d
x(t ) ↔ jω X ( jω )
dt
La diferenciación destruye cualquier componente dc de x(t): j 0 X ( j 0) = 0
No periódica :
FS:
x(t ) =
∞
∑ X [k ]e
jkω0t
∞
d
x(t ) = jkω0 ∑ X [k ]e jkω0t = jkω0 X [k ]
dt
k = −∞
;
k = −∞
Periódica :
FS ;ω0
d
x(t ) ↔ jkω0 X [k ]
dt
El valor promedio de la señal diferenciada sea cero : j 0 ω0 X (0) = 0
3.6.5 Diferenciación e integración, sumatoria y diferencia (cont.1)
Diferenciación en frecuencia
∞
FT: X ( jω ) = ∫ x(t )e − jω t dt
−∞
;
∞
d
X ( jω ) = ∫ (− jt x(t ) )e − jω t dt
−∞
dω
FT d
No periódica : − jt x(t ) ↔ dω X ( jω )
La diferenciación no se aplica a cantidades de valor discreto: FS, DTFS
DTFT: X (e jΩ ) =
∞
∑ x[n] e
n = −∞
− jΩ n
( )
∞
d
X e jΩ = ∑ (− jn x[n]) e − jΩ n
dΩ
n = −∞
DTFT
No periódica : − jn x[ n] ↔
d
X ( e jΩ )
dΩ
24
3.6.5 Diferenciación e integración, sumatoria y diferencia (cont.2)
x(t ) =
Sumatorio y diferencia
d
y (t ) ↔ x[n] = y[ n] − y[n − 1]
dt
t
y (t ) = ∫ x(τ )dτ ↔ y[n] =
−∞
DTFT
jΩ
(
x[n] ↔ X (e ) = 1 − e
− jΩ
)Y (e
jΩ
n
∑ x[k ]
k = −∞
)
X ( e jΩ )
+ πX (e j 0 )δ (Ω), − π < Ω < π
− jΩ
1− e
∞
∞
DTFT X (e jΩ )
j0
+
π
X
e
δ (Ω − k 2π )
x[k ]= y[n] ↔
(
)
∑
∑
1 − e − jΩ
k = −∞
k = −∞
DTFT
y[n] ↔ Y (e jΩ ) =
Integración
∫
FT
t
−∞
x(τ )dτ ↔
1
X ( jω ) + π X ( j 0)δ (ω )
jω
3.6.5 Diferenciación e integración, sumatoria y diferencia (resumen)
FT
d
x(t ) ↔ jω X ( jω )
dt
FS ;ω0
d
x(t ) ↔ jkω0 X [k ]
dt
FT
d
X ( jω )
dω
DTFT
d
X ( e jΩ )
dΩ
− jt x(t ) ↔
− jn x[n] ↔
∫
t
−∞
FT
x(τ )dτ ↔
∞
DTFT
∑ x[k ] ↔
k = −∞
1
X ( jω ) + π X ( j 0)δ (ω )
jω
∞
X ( e jΩ )
j0
+
π
X
e
(
)
∑ δ (Ω − k 2π )
1 − e − jΩ
k = −∞
25
3.6.6 Convolución y modulación
Convolución de señales no periódicas
∞
y (t ) = h(t ) * x(t ) = ∫ h(τ ) x(t − τ )dτ
−∞
∞
y (t ) = ∫ h(τ )
−∞
y (t ) =
1
2π
1
2π
∫
∞
; x(t − τ ) =
X ( jω )e jω t e − jωτ dω dτ =
−∞
1
ω
∫ [H ( jω ) X ( jω )]e dω = 2π ∫
∞
j t
−∞
∞
−∞
1
2π
1
2π
∫ ⎡⎢⎣∫
∫
∞
X ( jω )e jω (t −τ ) dω
−∞
∞
∞
−∞
−∞
h(τ )e − jωτ dτ ⎤ X ( jω )e jω t dω
⎥⎦
Y ( jω )e jω t dω
FT
y (t ) = h(t ) * x(t ) ↔ Y ( jω ) = H ( jω ) X ( jω )
DTFT
x[n] ↔ X (e jΩ )
DTFT
h[n] ↔ H (e jΩ )
⇒
DTFT
y[n] = x[n] * h[n] ↔ Y (e jΩ ) = X (e jΩ ) H (e jΩ )
3.6.6 Convolución y modulación (cont. 1)
Modulación , señales no periódicas
1
2π
1
z (t ) =
2π
x(t ) =
∫
∞
∫
∞
−∞
−∞
X ( jυ ) e jυ t d υ
Z ( jη )e jη t dη
FT
y (t ) = x(t ) z (t ) ←⎯→
Y ( jω ) =
1
X ( jω ) * Z ( jω )
2π
DTFT
x[n] ↔ X (e jΩ )
DTFT
jΩ
z[n] ↔ Z (e )
⇒
DTFT
⎯→ Y (e jΩ ) =
y[n] = x[n]z[n] ←⎯
convolución periódica (2π ) ⇒
X (e jΩ ) ⊗ Z (e jΩ ) = ∫
2π
1
X ( e jΩ ) ⊗ Z ( e jΩ )
2π
X (e jθ ) Z (e j ( Ω −θ )dθ
26
3.6.6 Convolución y modulación (cont. 2)
Convolución , señales periódicas
y (t ) = x(t ) ⊗ z (t ) = ∫ x(τ ) z (t − τ ) dτ
T
FS ; 2π / T
y (t ) = x(t ) ⊗ z (t ) ←⎯ ⎯
⎯→ Y [k ] = T X [k ] Z [k ]
y[n] = x[n] ⊗ z[n] =
∑ x[k ]z[n − k ]
K= N
DTFS ; 2π / N
y[n] = x[n] ⊗ z[n] ←⎯
⎯⎯
⎯→ Y [k ] = N X [k ] Z [k ]
Modulación , señales periódicas
FS ; 2π / T
y (t ) = x(t ) z (t ) ←⎯
⎯
⎯→ Y [k ] = X [k ] * Z [k ]
X [k ] * Z [k ] =
∞
∑ X [m]Z [k − m]
m = −∞
DTFS ; 2π / N
y[n] = x[n]z[n] ←⎯
⎯⎯
⎯→ Y (k ) = X (k ) ⊗ Z (k )
X (k ) ⊗ Z (k ) =
∑ X [m]Z [k − m]
m= N
3.6.6 Convolución y modulación (resumen)
Convolución
FT
h(t ) * x(t ) ↔ H ( jω ) X ( jω )
FS ;ω
x(t ) ⊗ z (t ) ←⎯⎯→ T X [k ] Z [k ]
DTFT
x[n] * h[n] ↔ X (e jΩ ) H (e jΩ )
Modulación
FT
x(t ) z (t ) ←⎯→
1
X ( j ω ) * Z ( jω )
2π
FS ;ω0
x(t ) z (t ) ←⎯
⎯→ X [k ] * Z [k ]
DTFT
x[n]z[n] ←⎯
⎯→
1
X (e jΩ ) ⊗ Z (e jΩ )
2π
DTFS ;Ω 0
DTFS ;Ω 0
x[n] ⊗ z[n] ←⎯
⎯⎯→ N X [k ] Z [k ] x[n]z[n] ←⎯ ⎯⎯→ X (k ) ⊗ Z (k )
27
3.6.7 Filtrado.
Modulación en el dominio de la frecuencia
Filtros : pasa baja, pasa alta, pasa banda y atenua banda
FT
y (t ) = h(t ) * x(t ) ↔ Y ( jω ) = H ( jω ) X ( jω )
X ( jω ) =
20 log H ( jω ) dB
1
Y ( jω ) = H inv ( jω ) Y ( jω )
H ( jω )
Espectro de energía :
2
2
Y ( jω ) = H ( jω ) X ( jω )
2
2
1
1
2
2
2
H ( jω c ) X ( jω c ) =
H ( jω c ) X ( jω c )
2
2
1
1
20 log
H ( jω ) dB = 20 log
dB + 20 log H ( jω ) dB = −3dB + 20 log H ( jω ) dB
2
2
2
Y ( jω c ) =
DTFT
x[n] * h[n] ↔ X (e jΩ ) H (e jΩ )
1
X ( e jΩ ) =
Y (e jΩ ) = H inv (e jΩ ) Y (e jΩ )
H ( e jΩ )
20 log H (e jΩ ) dB
Figure 3.53 (p. 263)
Frequency response of ideal continuous- (left panel) and discretetime (right panel) filters.
(a) Low-pass characteristic.
(b) High-pass characteristic.
(c) Band-pass characteristic.
28
Figure 3.54 (p. 264)
RC circuit with input x(t) and outputs yc(t) and yR(t).
t
1 − RC
e u (t )
RC
y R (t ) = x(t ) − yC (t )
hc (t ) =
hR (t ) = δ (t ) −
t
1 − RC
e u (t )
RC
Dibujar la respuesta en frecuencia de ambos sistemas
H C ( jω ) =
1
jωRC
; H R ( jω ) =
jωRC + 1
jωRC + 1
Figure 3.55a&c (p. 265)
RC circuit magnitude responses as a function of normalized frequency ωRC.
(a) Frequency response of the system b) Frequency response of the system
corresponding to yC(t), linear scale.
corresponding to yR(t), linear scale.
c) Frequency response of the system (d) Frequency response of the system
corresponding to yC(t), dB scale.
corresponding to yR(t), dB scale, shown on
the range from 0 dB to –25 dB.
29
Figure 3.55b&d (p. 265)
3.6.8 Relación de Parseval
La energía o potencia se conserva en le representación de Fourier
Energía de una señal no periódica x(t) :
2
∞
E x = ∫ x(t ) dt ;
−∞
∫
∞
−∞
2
x(t ) dt =
1
2π
∫
∞
−∞
2
x(t ) = x(t ) x* (t ) ;
2
X ( jω ) dω : Teorema de energía de Rayleigh
normalizado por 2π
2
H ( jω ) ⇒ espectro de energía de la señal
Energía : señales no periódicas en el dominio del tiempo
Potencia : señales periódicas en el dominio del tiempo ( sobre un
periodo normalizado)
30
3.6.8 Relación de Parseval (cont.)
FT
∫
FS
1
T
DTFT
∑
DTFS
1
N
Tiempo
2
∞
x(t ) dt =
−∞
∫
1
2π
∫
x(t ) dt = ∑k = −∞ X [k ]
∞
∞
1
x[n] =
2π
2
n = −∞
∑
2
X ( j ω ) dω
−∞
2
T
∞
∫π
2
2
jΩ
X ( e ) dΩ
x[n] =∑k = N X [k ]
2
n= N
No periódica (t,n)
Serie de Fourier
Tranformada de Fourier
x(t ) =
∑ X [k ]e
jkω0t
x(t ) =
k = −∞
1
T
X [k ] =
∫
T
0
x(t )e − jkω0t dt
1
2π
∫
∞
−∞
2
X ( jω )e jω t dω
∞
X ( jω ) = ∫ x(t )e − jω t dt
−∞
x(t) periodo T ⇒ ω0 = 2π T
x[n] =
∑ X [k ]e
jkΩ 0 n
x[n] =
k= N
X [k ] =
1
N
∑ x[n]e
π
jΩ
2π
N
( )
X e jΩ
jΩ n
−
X e jΩ =
n= N
Discreta (k)
∫ π X (e )e
( ) ∑ x[n] e
− jkΩ 0 n
x[n] y X[k] periodo N ⇒ Ω 0 =
1
2π
∞
dΩ
− jΩ n
n = −∞
tiene periodo 2π
Continua (ω,Ω)
Periódica (k,Ω)
Discreta [n]
Serie Fourier Tiempo Discr. Tranf. Fourier Tiempo Discr.
No periódica (k,ω)
Continua (t)
Periódica (t,n)
∞
2
Frecuencia
31
3.6.9 Dualidad
Dualidad de FT
FT
δ (t ) ↔ 1 ; − ∞ < ω < ∞
FT
1 ↔ 2πδ (ω )
Figure 3.73 (p. 307)
Duality of rectangular pulses and sinc
functions.
32
3.6.9 Dualidad (resumen)
FT
FT
f (t ) ←⎯→
F ( jω )
FT
F ( jt ) ←⎯→
2π f (−ω )
DTFS ; 2π / N
x[n] ←⎯
⎯⎯
⎯→ X [k ]
DTFS
DTFT y FS
DTFS ; 2π / N
X [n] ←⎯
⎯⎯
⎯→
DTFT
x[n] ←⎯
⎯→ X (e jΩ )
1
x[−k ]
N
FS ;1
X (e jΩ ) ←⎯
⎯→ x[− k ]
3.6.10 Producto tiempo-ancho de banda
Ancho de banda :¿contenido de frecuencia significativa de la señal?
“frecuencia a la cual el espectro de magnitud es 1 / 2 veces su valor
de pico”. Si x(t) está centrada en el origen y es paso bajas :
Duración de una señal = Td
Ancho de banda = Bw
∞
Td =
∫
∫
2
2
t x(t ) dt
−∞
∞
−∞
2
x(t ) dt
1
2
Bw =
∫
∞
ω X ( j ω ) dω
−∞
∞
∫
2
−∞
2
2
X ( j ω ) dω
1
2
1
2
principio de
incertidumbre
Td Bw ≥
33
Problema 3.48
Calcule los coeficientes del DTFS de la señal :
Por inspección
Problema 3.49
Dado los coeficientes del desarrollo DTFS, generar la señal
Por inspección
34
Problema 3.50
Calcule los coeficientes del FS de la señal :
Por inspección
Problema 3.51
Dado los coeficientes del desarrollo FS, generar la señal
35
Problema 3.52
Calcular la DTFT de la señal :
Problema 3.52 (cont.)
36
Problema 3.53
Calcular la la inversa de X ( e Ω )
a)
c)
Problema 3.54
Calcular la TF de la señal :
37
Problema 3.55
Calcular la inversa FT de X(jω)
a)
b)
Tiempo
No periódica (t,n)
Serie de Fourier
Tranformada de Fourier
x(t ) =
∞
∑ X [k ]e
jkω0t
x(t ) =
k = −∞
1
T
X [k ] =
∫
T
0
x(t )e − jkω0t dt
1
2π
∫
∞
−∞
X ( jω )e jω t dω
∞
X ( jω ) = ∫ x(t )e − jω t dt
−∞
x(t) periodo T ⇒ ω0 = 2π T
x[n] =
∑ X [k ]e
jkΩ 0 n
x[n] =
k= N
X [k ] =
1
N
∑ x[n]e
π
jΩ
2π
N
( )
X e jΩ
jΩ n
−
X e jΩ =
n= N
Discreta (k)
∫ π X (e )e
( ) ∑ x[n] e
− jkΩ 0 n
x[n] y X[k] periodo N ⇒ Ω 0 =
1
2π
∞
dΩ
− jΩ n
n = −∞
tiene periodo 2π
Continua (ω,Ω)
Periódica (k,Ω)
Discreta [n]
Serie Fourier Tiempo Discr. Tranf. Fourier Tiempo Discr.
No periódica (k,ω)
Continua (t)
Periódica (t,n)
Frecuencia
38
Problema 3.57a) Calcular la señal en el dominio del tiempo a partir
de su representación en el dominio de la frecuencia.
Periodo fundamental en el dominio del tiempo T=1
discreto y no periódico
FS ; 2π
←⎯
⎯→ periódico y continuo
Problema 3.58b) Calcular la señal en el dominio del tiempo a partir
de su representación en el dominio de la frecuencia.
DTFS ; 2π / 5
⎯ ⎯→
discreto y periódico ←⎯
discreto y periódico
39
Problema 3.58c) Calcular la señal en el dominio del tiempo a partir
de su representación en el dominio de la frecuencia.
DT
→ continuo y no periódico
continuo y no periódico ←⎯
Problema 3.58
Utilice la tabla de transformadas y las propiedades para calcular la FT
40
Problema 3.60
Utilice la tabla de transformadas y las propiedades para calcular la DTFT
Problema 3.68b
Determine la respuesta en frecuencia y la respuesta al impulso
para el sistema definido por la siguiente ecuación diferencial :
41
Problema 3.68c
Determine la respuesta en frecuencia y la respuesta al impulso
para el sistema definido por la siguiente ecuación diferencial :
Problema 3.73
Utilizar la descomposición en fracciones simples para calcular
la transformada inversa de Fourier de :
42
Problema 3.74
Utilizar la descomposición en fracciones simples para calcular
la transformada inversa de Fourier en tiempo discreto de :
43