ESTRUCTURA FINA DEL´ATOMO DE HIDR´OGENO.

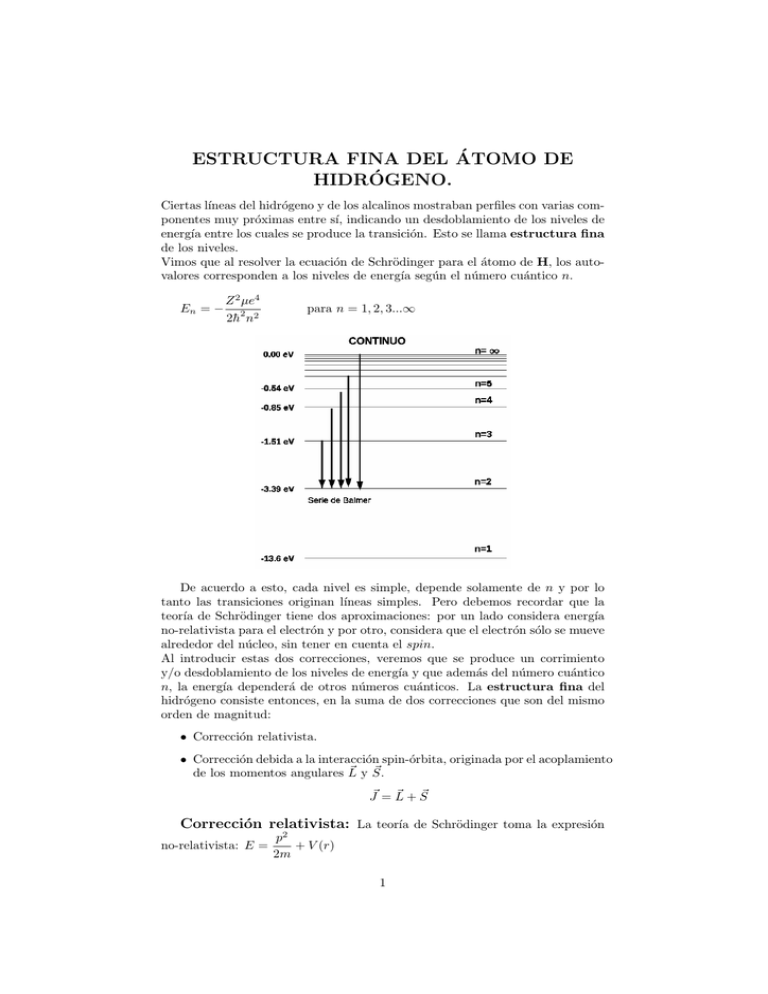
ESTRUCTURA FINA DEL ÁTOMO DE
HIDRÓGENO.
Ciertas lı́neas del hidrógeno y de los alcalinos mostraban perfiles con varias componentes muy próximas entre sı́, indicando un desdoblamiento de los niveles de
energı́a entre los cuales se produce la transición. Esto se llama estructura fina
de los niveles.
Vimos que al resolver la ecuación de Schrödinger para el átomo de H, los autovalores corresponden a los niveles de energı́a según el número cuántico n.
En = −
Z 2 µe4
2h̄2 n2
para n = 1, 2, 3...∞
De acuerdo a esto, cada nivel es simple, depende solamente de n y por lo
tanto las transiciones originan lı́neas simples. Pero debemos recordar que la
teorı́a de Schrödinger tiene dos aproximaciones: por un lado considera energı́a
no-relativista para el electrón y por otro, considera que el electrón sólo se mueve
alrededor del núcleo, sin tener en cuenta el spin.
Al introducir estas dos correcciones, veremos que se produce un corrimiento
y/o desdoblamiento de los niveles de energı́a y que además del número cuántico
n, la energı́a dependerá de otros números cuánticos. La estructura fina del
hidrógeno consiste entonces, en la suma de dos correcciones que son del mismo
orden de magnitud:
• Corrección relativista.
• Corrección debida a la interacción spin-órbita, originada por el acoplamiento
~ y S.
~
de los momentos angulares L
~ +S
~
J~ = L
Corrección relativista: La teorı́a de Schrödinger toma la expresión
no-relativista: E =
p2
+ V (r)
2m
1
Expresión correcta siempre que la velocidad del electrón sea pequeña respecto
a c. Pero vimos (modelo de Bohr), que la velocidad máxima del electrón, para
vmax
n = 1, vale vmax = 2.2 × 108 cm/s, por lo tanto,
∼ 7 × 10−3 ∼ 1%
c
Si bien la relación es pequeña, existen efectos relativistas que pueden ser observables. Si m0 es la masa en reposo del electrón:
q
T = c2 p2 + m20 c4 − m0 c2
q
Er = c2 p2 + m20 c4 − m0 c2 + V (r)
#
"µ
¶1/2
c2 p2
2
Er = m0 c
1+ 2 4
− 1 + V (r)
m0 c
Considerando que m0 v ¿ m0 c, tomamos ² =
serie:
(1 + ²)1/2 ∼ 1 + 21 ² − 18 ²2 + ...
·
Er = m0 c2 1 +
p2
¿ 1 y desarrollamos en
m20 c2
¸
p2
p4
−
−
1
+ V (r)
2m20 c2
8m40 c4
· 2
¸
p
p4
Er =
+ V (r) −
2m0
8m30 c2
Los dos primeros términos corresponden a la expresión clásica de la energı́a
y el tercer término es la corrección relativista de primer orden.
∆Er = −
m0 v 4
9.11 × 10−28 (2.2 × 108 )4
p4
=
∼
−
8m30 c2
8c2
8(3 × 1010 )2
∆Er = −3 × 1016 erg = 2 × 10−4 eV
Se trata como una pequeña perturbación y podemos estimar su valor medio
usando las autofunciones normalizadas:
∆Er = −
1
8m30 c2
Z
V ol
∗
ψnlm
p4 ψnlm dV
RhcZ α ³ 3
4n −
n3
4 2
∆Er =
1
l+1/2
´
(1)
2
e
1
α = h̄c
∼ 137
Se denomina constante de estructura fina.
Como l ≤ n, siempre tendremos que ∆Er < 0, es decir, provoca un corrimiento
del nivel hacia valores más negativos.
La correción relativista depende de n y l y destruye la degeneración respecto a
este último número cuántico. Para un n dado, cuanto menor es el l, mayor es
la corrección.
Si expresamos (1) en número de ondas:
∆Tr =
RZ 4 α2 ³ 3
4n −
n3
2
1
l+1/2
´
cm−1
(2)
Interacción spin-órbita:
Consideremos al electrón moviéndose en una órbita circular y masa del
núcleo infinita, por lo tanto despreciamos efectos debidos al movimiento del
~
núcleo. El electrón se mueve con una velocidad v en un campo eléctrico E
producido por el núcleo.
Tomaremos dos sistemas de referencia inerciales: S en el cual el núcleo está
en reposo y S 0 en el que instantáneamente el electrón está en reposo. Para el
~
sistema S 0 el núcleo se mueve con una velocidad −v que es perpendicular a E
en cada instante en que el electrón se considera en reposo. Para el electrón en
S 0 el núcleo cargado genera una corriente ~j
~j = − Ze~v
c
Según la ley de Ampére, el campo magnético producido por esa corriente en el
lugar donde se halla el electrón es:
~
~ = j × ~r = − Ze (~v × ~r)
B
r3
cr3
~ = Ze~r
E
r3
~
~ = − (~v × E)
B
c
En el sistema S 0 el electrón ”ve” un campo magnético y habrá una energı́a
de interacción entre el campo y el momento magnético de spin µs . Como en
este sistema de referencia estamos considerando fijo al electrón, L = 0 y µl = 0.
La energı́a de interacción en S 0 será:
~
∆E 0 = −~
µs B
µB ~
S
h̄
µB ~ ~
SB
∆E 0 = gs
h̄
µ
~ s = −gs
3
~ es generar un
Vimos en capı́tulos anteriores que el efecto del campo B
movimiento de precesión de µ
~ s alrededor del campo con una frecuencia llamada
frecuencia de Larmor:
µB ~
ω
~ L = gs
B
h̄
~
∆E 0 = ω
~ LS
Ahora bien, estas expresiones corresponden al sistema S 0 y lo que realmente
interesa es conocer sus valores en el marco de referencia donde el núcleo está en
reposo y el que se mueve es el electrón. Se puede demostrar que al transformar
al sistema S, cambiará la precesión de Larmor:
ωL → ω, donde ω = ωL + ωT
ωT se llama precesión de Thomas y representa la precesión del sistema S 0
respecto al marco normal. Su valor resulta ser:
ωT = − 21 ωL =⇒ ω = 12 ωL
De donde resulta que en el marco normal S, la energı́a de interacción será:
∆ELS =
Pero:
1 ~
gs e ~ ~
BS
ω
~ LS =
2
2 2mc
~ = − Ze (~v × ~r) = Ze m(~r × ~v ) = Ze L
~
B
cr3
mcr3
mcr3
Reemplazando:
∆ELS =
Ze2 ~ ~
LS
2m2 c2 r3
Ze2 1
ˆ
LS cos LS
2m2 c2 r3
ˆ deben permanecer inPor conservación del momento angular, J~ y el ángulo LS
ˆ medianvariantes durante la precesión. Podemos evaluar el producto LS cos LS
te el diagrama vectorial:
∆ELS =
ˆ = L2 + S 2 + 2LS cos LS
ˆ
J 2 = L2 + S 2 − 2LS cos(π − LS)
ˆ =
LS cos LS
1 2
(J − L2 − S 2 )
2
4
Reemplazando:
Ze2 1 2
(J − L2 − S 2 )
4m2 c2 r3
1
Como r depende de Z, n, l el término 3 cambia para cualquier estado, por
r
lo tanto se obtiene un valor medio:
Z ∞ Z π Z 2π
1
1
∗
ψnljm
< 3 >=
ψnljmj r2 sin θdrdθdϕ
j 3
r
r
r=0 θ=0 ϕ=0
∆ELS =
<
r1 =
Z3
1
>=
r3
r13 n3 l(l + 12 )(l + 1)
h̄2
es el radio de la primera órbita de Bohr.
me2
Introducimos las constantes:
e2
1
α=
∼
constante de estructura fina
h̄c
137
4
me
constante de Rydberg
R=
4πh̄3 c
2
Rα = 5.819cm−1
∆ELS =
Z 4 Rα2 hc
[j(j + 1) − l(l + 1) − s(s + 1)]
2n3 l(l + 12 )(l + 1)
(3)
Expresada en número de ondas:
Z 4 Rα2
∆TLS (cm−1 ) = 3
[j(j + 1) − l(l + 1) − s(s + 1)]
2n l(l + 12 )(l + 1)
O bien:
∆TLS (cm−1 ) =
donde:
a(cm−1 ) =
a
2
[j(j + 1) − l(l + 1) − s(s + 1)]
(4)
Z 4 Rα2
n3 l(l + 12 )(l + 1)
De acuerdo a (3) y (4), la interacción spin-órbita indica que los números
cuánticos necesarios para especificar el estado del electrón son n, l, j. La energı́a
depende de ellos, pero subsiste la degeneración respecto al número cuántico mj .
Veremos más adelante que se destruye esta degeneración cuando consideramos
un átomo en un campo magnético externo (Efecto Zeeman).
Cuando l = 0 (estados s), el nivel es simple y no hay corrimiento (∆ELS =
0). Siempre s = 1/2 y para cada valor de l, el número cuántico j toma dos
~ puede tener sólo dos orientaciones
valores: j = (l+1/2) y j = (l−1/2), ya que S
posibles. Es decir la multiplicidad de los niveles será 2.
La nomenclatura utilizada para designar cada nivel es:

l=0 Términos S



l=1 Términos P
2
lj
Si
l=2 Términos D



...
......
...
5
Como la corrección relativista y la interacción spin-órbita son del mismo
orden, podemos sumar (2) y (4), para obtener la expresión final de la estructura
fina:
∆T EF (cm−1 ) = ∆T r + ∆T LS
·
¸
1
[j(j + 1) − l(l + 1) − s(s + 1)]
RZ 4 α2 3
−1
−
+
∆T EF (cm ) =
n3
4n l + 1/2
2l(l + 1/2)(l + 1)
·
¸
RZ 4 α2 3
1
∆T EF (cm−1 ) =
−
(5)
n3
4n j + 1/2
La expresión entre corchetes es siempre negativa, por lo tanto los niveles se
corren hacia abajo (valores más negativos). Vemos además que la estructura
fina, desarrollada hasta el primer orden de aproximación, depende solamente de
n y j:
·
¸
1
RZ 2
RZ 4 α2 3
Tnj (cm−1 ) = − 2 +
−
(6)
n
n3
4n j + 1/2
Veamos la estructura fina de los 3 primeros niveles del hidrógeno:
n
1
2
3
l
0
0
1
0
1
2
s
1/2
1/2
1/2
1/2
1/2
1/2
j
1/2
1/2
1/2,3/2
1/2
1/2,3/2
3/2,5/2
Config-electr.
1s
2s
2p
3s
3p
3d
Niveles
2
S1/2
2
S1/2
2
P1/2 ,2 P3/2
2
S1/2
2
P1/2 ,2 P3/2
2
D3/2 ,2 D5/2
De acuerdo a (5) el desplazamiento de los niveles de estructura fina serán:
n
1
2
3
Niveles
2
S1/2
2
S1/2 , 2 P1/2
2
P3/2
2
S1/2 , 2 P1/2
2
P3/2 , 2 D3/2
2
D5/2
∆T EF (cm−1 )
-1.45
-0.455
-0.091
-0.161
-0.053
-0.018
Las transiciones entre estos niveles están regidas por las reglas de selección, las que indican qué cambios en los números cuánticos dan las transiciones más probables :
∆l = ±1
∆j = 0, ±1
Por ejemplo la transición n = 3 → n = 2, correspondiente a la lı́nea Hα de la
Serie de Balmer, son en realidad 5 transiciones de estructura fina:
2
D5/2 →2 P3/2
2
D3/2 →2 P3/2
6
2
S1/2 →2 P3/2
D3/2 →2 P1/2 ó 2 P3/2 →2 S1/2
2
P1/2 →2 S1/2 ó 2 S1/2 →2 P1/2
2
El perfil de Hα tendrá cinco componentes muy cercanas y de distintas intensidades. Las más intensas corresponden a las dos transiciones que involucran
los mayores valores de j (2 D5/2 →2 P3/2 y 2 D3/2 →2 P3/2 ) y las tres restantes
son más dédiles.
7