Todos los ejercicios del libro hechos

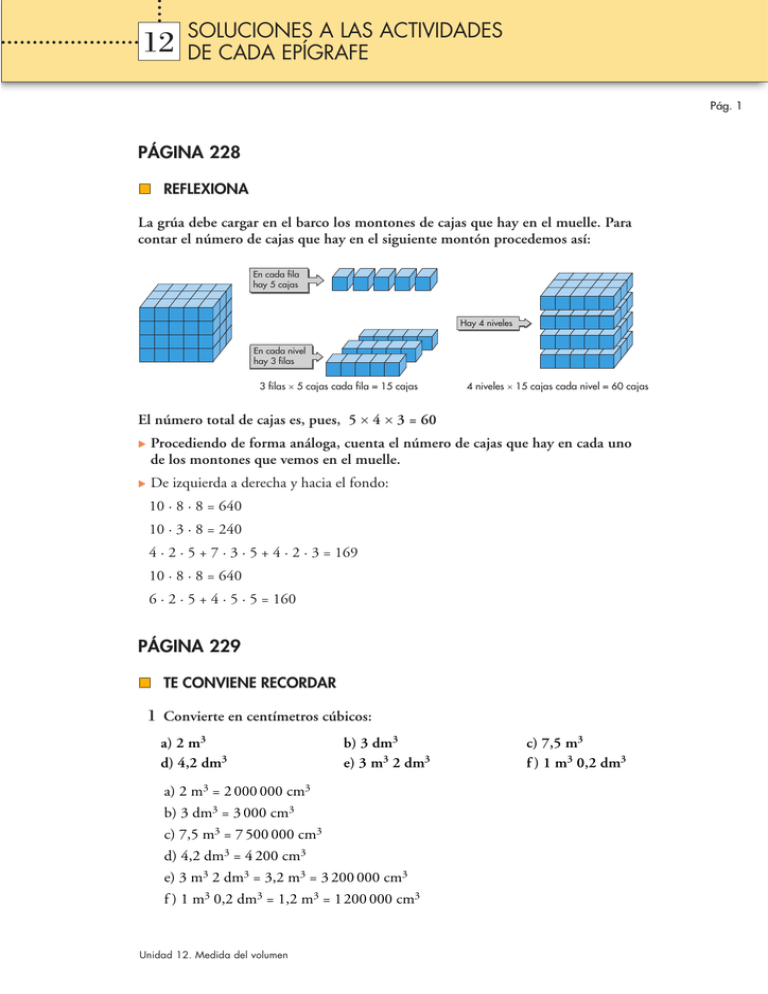
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 1
PÁGINA 228
REFLEXIONA
La grúa debe cargar en el barco los montones de cajas que hay en el muelle. Para
contar el número de cajas que hay en el siguiente montón procedemos así:
En cada fila
hay 5 cajas
Hay 4 niveles
En cada nivel
hay 3 filas
3 filas × 5 cajas cada fila = 15 cajas
4 niveles × 15 cajas cada nivel = 60 cajas
El número total de cajas es, pues, 5 × 4 × 3 = 60
Procediendo de forma análoga, cuenta el número de cajas que hay en cada uno
de los montones que vemos en el muelle.
De izquierda a derecha y hacia el fondo:
10 · 8 · 8 = 640
10 · 3 · 8 = 240
4 · 2 · 5 + 7 · 3 · 5 + 4 · 2 · 3 = 169
10 · 8 · 8 = 640
6 · 2 · 5 + 4 · 5 · 5 = 160
PÁGINA 229
TE CONVIENE RECORDAR
1 Convierte en centímetros cúbicos:
a) 2 m3
d) 4,2 dm3
b) 3 dm3
e) 3 m3 2 dm3
a) 2 m3 = 2 000 000 cm3
b) 3 dm3 = 3 000 cm3
c) 7,5 m3 = 7 500 000 cm3
d) 4,2 dm3 = 4 200 cm3
e) 3 m3 2 dm3 = 3,2 m3 = 3 200 000 cm3
f ) 1 m3 0,2 dm3 = 1,2 m3 = 1 200 000 cm3
Unidad 12. Medida del volumen
c) 7,5 m3
f ) 1 m3 0,2 dm3
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 2
2 Expresa en litros:
a) 4 dm3
b) 2 m3
c) 2,5 m3
d) 500 cm3
a) 4 dm3 = 4 l
b) 2 m3 = 2 000 dm3 = 2 000 l
c) 2,5 m3 = 2 500 dm3 = 2 500 l
d) 500 cm3 = 0,5 dm3 = 0,5 l
3 ¿Cuántos kilos pesa el agua que cabe en una bolsa de 17,84 m3?
17,84 m3 pesan 17,84 toneladas = 17 840 kilos
PÁGINA 230
1 Expresa en dm3:
a) 3 hm3 253 dam3 124 m3 450 dm3
b) 526 890 cm3
c) (580 cm3 800 mm3) · 20 000
d) 2 km3 150 dam3 25 dm3 780 mm3
a) 3 253 124 450 dm3
b) 526,890 dm3
c) (0,580800 dm3) · 20 000 = 11616 dm3
d) 2 000 150 000 025,00078 dm3
2 Expresa en distintas unidades (pasa a forma compleja):
a) 324 526 943,86 dm3
b) (394 540 cm3) · 400 000
c) 0,0000864 hm3
a) 324 dam3 526 m3 943 dm3 860 cm3
b) 157 816 000 000 cm3 = 157 dam3 816 m3
c) 86 m3 400 dm3
Unidad 12. Medida del volumen
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 3
PÁGINA 231
1 Añade la unidad en la que se expresa cada uno de los siguientes volúmenes:
a) Capacidad de un vaso: 1/4
o bien 250
b) Una cucharadita: 6
c) Consumo bimensual de agua en una casa: 63,834
d) Agua en un pantano: 680
a) 1/4 l o 250 cm3
b) 6 ml
c) 63,834 m3
d) 680 hm3
2 Expresa en litros:
a) 36 dam3 43 m3 114 dm3 500 cm3
b) 3 860 000 mm3
c) 0,0089 hl
a) 36 043 114,5 dm3 = 36 043 114,5 l
b) 3,86 dm3 = 3,86 l
c) 8 900 l
3 Expresa en unidades de volumen (forma compleja):
a) (386 500 dl ) · 40
b) (596 800 kl ) · 0,4
a) 15 460 000 dl = 15 460 l = 15 460 dm3 = 15 m3 460 dm3
b) 238 720 kl = 238 720 m3 = 238 dam3 720 m3
PÁGINA 232
1 Con una cartulina como la que aquí aparece se puede construir una caja cortando un cuadrado en cada esquina. Por ejemplo:
} 1 cm
Unidad 12. Medida del volumen
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 4
Halla el volumen de esta caja y los de las cajas esquinas cuadraditos de 1 × 1
y de 3 × 3.
• Volumen de la caja suprimiendo 2 × 2 cuadraditos:
V = 6 · 2 · 3 = 36 cm3
• Suprimiendo 1 × 1 cuadraditos:
V = 8 · 1 · 5 cm3 = 40 cm3
• Suprimiendo 3 × 3 cuadraditos:
V = 4 · 3 · 1 = 12 cm3
2 Contesta antes de realizar ningún cálculo: ¿Cuántas duchas crees que podrías
darte con el agua que cabe en tu aula?
Ahora haz los cálculos para un aula de 6 m de ancha, 10 m de larga y 2,5 m
de alta, a razón de 100 l de agua para cada ducha.
Actividad de respuesta abierta, condicionada a las dimensiones del aula. Se debe tantear el número de litros que pueden caber en el aula.
Volumen = 6 · 10 · 2,5 = 150 m3
150 m3 = 150 000 dm3 = 150 000 l
150 000 : 100 = 1 500 duchas
3 Aplicando la fórmula para
1,2 m
1,8 m
1,3 m
calcular el volumen de un ortoedro, averigua el volumen
de este objeto:
1,5 m
1,8 m
1,3 m
3,5 m
1,
1
m
1,2 m
1
0,8 m
3,5 m
1,
0,5 m
m
1,5 m
V = 1,2 · 1,8 · 1,1 + 1,5 · 0,5 · 1,1 + 0,8 · 0,5 · 1,1 = 2,376 + 0,825 + 0,22 = 3,421 m3
2
Unidad 12. Medida del volumen
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 5
4 La suma de todas las aristas de un cubo es de 60 cm. Halla su volumen.
Un cubo tiene 12 aristas, todas ellas de la misma dimensión.
12a = 60 → a = 5 cm
V = 53 = 125 cm3
PÁGINA 233
1 La base de un paralelepípedo es un rombo de diagonales de 10 cm y 20 cm.
Su altura es de 15 cm. Halla su volumen.
15 cm
10
c
20 cm m
Área de la base = 10 · 20 = 100 cm2
2
Volumen = 100 · 15 = 1500 cm3
paralelepípedo así:
m
6c
6 cm
2 Con seis rombos iguales se puede construir un
a) Dibuja una cara. Comprueba, midiéndola,
que la distancia entre dos lados opuestos es
de 5,2 cm. Calcula el área de esa cara y el área total del paralelepípedo.
b) La distancia entre dos caras opuestas del paralelepípedo es de 4,9 cm. Calcula el volumen del cuerpo.
c) Constrúyelo.
)
a)
m
6c
6 cm
5,2
cm
Acara = 6 · 5,2 = 31,2 cm2
2
Atotal = 6 · 31,2A = 187,2
= 6 · cm
5,2 = 31,2 cm2
cara
Unidad 12. Medida del volumen
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 6
b) V = 31,2 · 4,9 = 152,88 cm3
c) Actividad de construcción. Proponemos aquí un posible desarrollo:
(NOTA: el desarrollo está reducido al 70% de su tamaño real)
Unidad 12. Medida del volumen
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 7
PÁGINA 234
1 Halla el volumen de una habitación de 2,8 m
10 m
de altura, cuya planta tiene la siguiente forma y
dimensiones:
4m
2m
2m
10 m
A1
2m
A3
A2
4m
2m
A3
A4
A1 = 4 · 10 = 40 m2
A2 = 6 · 2 = 12 m2
2
A3 = π · 2 = 3,14 m2
4
2
A4 = π · 3 = 14,13 m2
2
Área de la base = A1 + A2 + 2A3 + A4 = 72,41 m2
Volumen = 72,41 · 2,8 = 202,748 m3
2 Halla el volumen de los siguientes cuerpos geométricos:
a)
a
h
r = 30 cm
b)
l
a = 26 cm
l = 30 cm
h=1m
h=1m
Vprisma = 6 · 30 · 26 · 100 = 234 000 cm3 = 234 dm3 = 0,234 m3
2
Vcilindro = π · 302 · 100 = 282 600 cm3 = 282,61 dm3 = 0,2826 m3
PÁGINA 235
1 Recordemos la descripción que se hacía de la gran pirámide de Keops en la unidad 11. Es una pirámide cuadrangular regular. El lado de la base mide 240 m y
la altura, 160 m. Calcula cuántos hectómetros cúbicos tiene de volumen.
V = 1 · 2402 · 160 = 3 072 000 m3 = 3,072 hm3
3
Unidad 12. Medida del volumen
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 8
2 Calcula el volumen de esta pirámide hexagonal regular:
 lado = 30 cm
Base 
 apotema = 26 cm
h
Altura = 80 cm
V = 1 · 6 · 30 · 26 · 80 = 62 400 cm3 = 62,4 dm3
3
2
l
a
PÁGINA 236
1 Halla el volumen de este embudo (prescindir del pitorro y considerar que es un cono).
Radio de la base: 10 cm
Altura: 14 cm
)
V = 1 π · 102 · 14 = 1465,3 cm3
3
2 Halla el volumen de esta flanera, sabiendo que los radios de sus bases miden 10 cm y 15 cm y su altura,
12 cm.
15 m
12 m
10 m
x
x + 12 = x → 10x + 120 = 15x → 5x = 120 → x = 24 cm
15
10
Vcono grande = 1 π · 152 · 36 = 8 478 cm3
3
Vcono pequeño = 1 π · 102 · 24 = 2 512 cm3
3
Vtronco de cono = 8 478 – 2 512 = 5 966 cm3
Unidad 12. Medida del volumen
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 9
PÁGINA 237
1 Tenemos un cajón cúbico de 40 cm de lado lleno en sus tres cuartas partes de
bolitas de poliexpán (corcho blanco). Queremos ocultar en su interior un balón de 32 cm de diámetro. ¿Qué volumen de corcho sobra?
3 · 403 + 4 π · 163 = 48 000 + 17 148,6 = 65148,6
4
3
65148,6 – Vcubo = 65148,6 – 64 000 = 1148,6 cm3
Sobran 1148,6 cm3 de poliexpán.
2 Un bote cilíndrico de 5 cm de radio y 30 cm de altura contiene
tres pelotas de tenis bien encajadas. Calcula el volumen de aire
que hay en su interior.
Vbote = π · 52 · 30 = 2 355 cm3
Las esferas (pelotas) ocupan 2 del volumen del cilindro (bote).
3
Por tanto, el aire que queda en el interior es:
1 · 2 355 cm3 = 785 cm3
3
Unidad 12. Medida del volumen
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 1
PÁGINA 238
EJERCICIOS DE LA UNIDAD
Unidades de volumen
1
2
Transforma en metros cúbicos:
a) 450 dam3
b) 0,084 hm3
c) 0,11 km3
d) 35 840 dm3
e) 500 hl
f ) 30 000 l
a) 450 dam3 = 450 000 m3
b) 0,084 hm3 = 84 000 m3
c) 0,11 km3 = 110 000 000 m3
d) 35 840 dm3 = 35,84 m3
e) 500 hl = 50 m3
f ) 30 000 l = 30 m3
Transforma en litros los siguientes volúmenes:
a) 11 dam3 350 m3
b) 0,87 hl
c) 0,000094 hm3
d) 300 000 mm3
a) 11 dam3 350 m3 → 11 350 000 l
b) 0,87 hl → 87 l
c) 0,000094 hm3 → 94 000 l
d) 300 000 mm3 → 0,3 l
3
Completa las siguientes igualdades:
a) 0,0013 hm3 = ...................................... dm3
b) 0,11 dam3 = ........................................ cm3
c) 3 dam3 11 m3 743 dm3 = .................... m3
d) 3 dam3 11 m3 743 dm3 = ................. l
a) 0,0013 hm3 = 1300 000 dm3
b) 0,11 dam3 = 110 000 000 cm3
c) 3 dam3 11 m3 743 dm3 = 3 011,743 m3
d) 3 dam3 11 m3 743 dm3 = 3 011 743 l
Unidad 12. Medida del volumen
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 2
4
Expresa como suma de unidades de volumen (forma compleja):
a) 75 427 038 m3
b) 32,14962 dm3
c) 0,0000084 km3
d) 832 000 dam3
a) 75 427 038 m3 → 75 hm3 427 dam3 38 m3
b) 32,14962 dm3 → 32 dm3 149 cm3 620 mm3
c) 0,0000084 km3 → 8 dam3 400 m3
d) 832 000 dam3 → 832 hm3
6
¿Cuántas botellas de 3/4 l se pueden llenar con 0,4 dam3?
0,4 dam3 = 400 000 l
)
400 000 : 3 = 533 333, 3 botellas
4
Se pueden llenar unas 533 333 botellas.
7
Un pantano tiene una capacidad de 0,19 km3. Si ahora está al 28% de
su capacidad, ¿cuántos litros de agua contiene?
28% de 0,19 km3 = 0,0532 km3 = 53 200 000 000 l
8
La cuenca fluvial cuyas aguas llegan a un pantano es de 62 km2. En las
últimas lluvias han caído 27 l por metro cuadrado. Del agua caída, se recoge
en el pantano un 43%. ¿Cuántos metros cúbicos de agua se han recogido en
el pantano como consecuencia de las lluvias?
62 km2 = 62 000 000 m2
62 000 000 · 27 · 43 = 719 820 000 l = 719 820 m3
100
9
¿Cuál es la masa de 0,0843 dam3 de agua?
0,0843 dam3 = 84 300 l
Su masa es de 84 300 kg.
10
Un depósito vacío pesa 27 kg y lleno de aceite 625,5 kg. ¿Qué volumen
de aceite contiene? La densidad de ese aceite es 0,95 kg/dm3.
625,5 – 27 = 598,5 kg de aceite
598,5 : 0,95 = 630 l de aceite
Unidad 12. Medida del volumen
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 3
11
Efectúa las operaciones siguientes y expresa el resultado en hectolitros:
a) 0,46 dam3 + 47 m3 + 5 833 m3
b) 0,00084 km3 + 0,31 hm3 + 33 dam3
c) 0,413 dam3 – 315 m3 800 dm3
d) 2 300 m3 : 25
a) 0,46 dam3 + 47 m3 + 5 833 m3 = 460 m3 + 47 m3 + 5 833 m3 = 6 340 m3 =
= 6 340 kl = 63 400 hl
b) 0,00084 km3 + 0,31 hm3 + 33 dam3 = 840 dam3 + 310 dam3 + 33 dam3 =
= 1 183 dam3 = 11830 000 hl
c) 0,413 dam3 – 315 m3 800 dm3 = 413 000 dm3 – 315 800 dm3 = 97 200 dm3 =
= 972 hl
d) 2 300 m3 : 25 = 92 m3 = 92 kl = 920 hl
12
Completa estas igualdades:
a) 1 hm3 =........................................ hl
b) 1 dam3 =...................................... dal
c) 1 m3 =.......................................... l
d) 1 dm3 = ....................................... dl
e) 1 cm3 = ........................................ cl
f ) 1 mm3 = ...................................... ml
13
a) 1 hm3 = 10 000 000 hl
b) 1 dam3 = 100 000 dal
c) 1 m3 = 1000 l
d) 1 dm3 = 10 dl
e) 1 cm3 = 0,1 cl
f ) 1 mm3 = 0,001 ml
Estimación de volúmenes “a ojo”
Para cada uno de los recipientes que se citan a continuación se dan tres volúmenes. Solo uno de ellos es razonable. Di, en cada caso, cuál es:
a) Volumen de un pantano:
11 hm3; 387 000 l ; 4 000 000 000 cm3
b) Un depósito de agua en una vivienda:
2 dam3; 0,8 m3; 45 000 l
Unidad 12. Medida del volumen
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 4
c) Un vaso normal:
2 dm3; 0,2 dm3; 0,02 dm3
d) Una cuchara de café:
8 dl ; 8 cm3; 8 mm3
e) Una habitación:
1 dam3; 300 l ; 30 m3
f ) El cajón de una mesa:
0,3 m3; 30 dm3; 3 000 cm3
a) 11 hm3 (un pantano pequeño)
b) 0,8 m3 = 800 l
c) 0,2 dm3 = 1/5 l
d) 8 cm3 = 0,008 l
e) 30 m3
f ) 30 dm3
PÁGINA 239
CÁLCULO DE VOLÚMENES
14
Calcula el volumen de un ortoedro cuyas dimensiones son 3 cm × 5 cm ×
11 cm.
V = 3 · 5 · 11 = 165 cm3
15
¿Cuál es el volumen de un cubo de 12 cm de arista?
V = 123 = 1 728 cm3
16
La base de un prisma recto es un triángulo rectángulo cuyos catetos miden 11,3 cm y 6,8 cm. La altura del prisma es de 2 dm. Halla su volumen.
Abase = 11,3 · 6,8 = 38,42 cm2
2
V = 38,42 · 20 = 768,4 cm3
17
Un paralelepípedo tiene unas bases en forma de rombo
cuyas diagonales miden 7 dm y 4 dm. La altura del paralelepípedo es de 1,2 m. Halla su volumen.
V = 7 · 4 · 12 = 168 dm3
2
Unidad 12. Medida del volumen
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 5
18
Halla el volumen de un cilindro de 10 dm de radio de la base y 20 dm
de altura.
y
V = π · 102 · 20 = 6 280 dm3
19
Halla el volumen de una esfera de 25 cm de radio.
V = 4 π · 253 = 65 416,67 cm3
3
20
Halla el volumen de un cono de 6 dm de radio de la base y 15 cm de altura.
V = 1 π · 602 · 15 = 56 520 cm3
3
21
Halla el volumen del siguiente tronco de cono:
15 cm
20 cm
12 cm
15 cm
15 = 20 → x = 9 cm
x
12
x
V = 1 (π · 122 · 20 – π · 92 · 15) = 1742,7 cm3
3
5 cm
12 cm
30
cm
30 cm
Vesfera = 4 π · 153 = 14130 cm3
3
Vcilindro = π · 152 · 30 = 21195 cm3
Vesfera + Vcono = 21195 cm3 = Vcilindro
Unidad 12. Medida del volumen
30 cm
Comprueba que el volumen del cilindro es igual a la suma de los volúmenes de la esfera y el cono:
30 cm
22
30 cm
Vcono = 1 π · 152 · 30 = 7 065 cm3
3
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 6
Halla el volumen de las siguientes figuras:
23
BASES
3 dm
14 cm
11 cm
20 cm
Abase = (14 + 20) · 11 = 187 cm2
2
V = 187 · 30 = 5 610 cm3
24
a)
b)
12 cm
11 cm
5 cm
5 cm
8 cm
a) V = 1 π · 52 · 12 = 314 cm3
3
25
b) V = 8 · 5 · 11 = 440 cm3
a)
b)
11 cm
6 cm
10 cm
8 cm
x = x + 10 → 8x = 6x + 60 → 2x = 60 → x = 30 cm
6
8
Vcono grande = 1 π · 82 · 40 = 2 679,47 cm3
3
a)
x
Vcono pequeño = 1 π · 62 · 30 = 1130,4 cm3
3
6 cm
10 cm
Vtronco de cono = 2 679,47 – 1130,4 = 1549,07 cm3
8 cm
3
b) V = (4/3) π · 5,5 = 348,28 cm3
2
Unidad 12. Medida del volumen
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 7
26
b)
20 dm
12 cm
a)
6 dm
3 cm
14 dm
a) V = 20 · 14 · 6 = 840 dm3
2
27
b) V = π · 32 · 12 = 339,12 cm3
a)
b)
5c
m
26 cm
22 cm
40°
12
cm
13 cm
(
)
a) V = 1 12 · 5 · 22 = 220 cm3
3
2
b) 360° = 40°
9
V = 1 · 4 π · 133 = 1022,01 cm3
9 3
PÁGINA 240
Teniendo en cuenta las medidas señaladas, halla el volumen de las siguientes figuras:
28
30 cm
12 cm
Unidad 12. Medida del volumen
V = π · 122 · 30 + 4 π · 123 = 20 799,36 cm3
3
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 8
30 cm
29
V = 1 π · 122 · 30 + 1 · 4 π · 123 = 8138,88 cm3
3
2 3
12 cm
30
30 cm
18 cm
V = 1 · 4 π · 153 – 1 · 4 π · 93 = 7 065 – 1526,04 = 5 538,96 cm3
2 3
2 3
31
10 cm
15 cm
Vcilindro = π · 52 · 15 = 1177,5 cm3
8 cm
Vcono = 1 π · 102 · 15 = 1 570 cm3
3
15 cm
20 cm
x = x + 8 → 10x = 5x + 40 → 5x = 40 → x = 8 cm
5
10
Vtronco de cono = 1 (π · 102 · 16 – π · 52 · 8) = 1465,3 cm3
3
Vtotal = 1177,5 + 1570 + 1465,3 = 4 212,8 cm3
Unidad 12. Medida del volumen
x
5 cm
8 cm
10 cm
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 9
PROBLEMAS
32
Halla el volumen de una habitación que mide 6 m × 3,8 m × 2,6 m.
¿Cuántas duchas podrías darte con el agua que cabe en la habitación suponiendo que gastas 120 l de agua en cada ducha?
V = 6 · 3,8 · 2,6 = 59,28 m3
59,28 m3 = 59 280 dm3 = 59 280 l
59 280 : 120 = 494
Se podría dar 494 duchas.
33
Un aljibe de base rectangular de 6,4 m × 3,8 m tiene una profundidad
de 4,8 m y está lleno hasta los 3/4 de su volumen. Se sacan 340 hectolitros.
¿Qué altura alcanzará el agua?
Valjibe = 6,4 · 3,8 · 4,8 = 116,736 m3
3 V = 3 116,736 = 87,552 m3 = 87,552 kl = 875,52 hl
4
4
875,52 hl – 340 hl = 535,52 hl = 53,552 m3
Vagua = 53,552 m3 = 6,4 · 3,8 · h → h = 53,552 = 2,202 m
6,4 · 3,8
El agua alcanzará una altura de 2,202 m.
34
Calcula el volumen de hormigón que se ha necesitado para hacer este
túnel:
8m
10 m
Vcilindro grande = π · 52 · 20 = 1570 m3
Vcilindro pequeño = π · 42 · 20 = 1004,8 m3
Vhormigón = 1570 – 1004,8 = 282,6 m3
2
Unidad 12. Medida del volumen
20 m
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 10
35
Para medir el volumen de una piedra pequeña procedemos del siguiente modo: en una vasija cilíndrica echamos
agua hasta la mitad, aproximadamente. Sumergimos la piedra y sube el nivel 22 mm. ¿Cuál es el volumen de la piedra?
DATOS DE LA VASIJA:
Diámetro exterior: 9 cm
Diámetro interior: 8,4 cm
Altura: 15 cm
(Usa solo los datos que necesites).
Radio interior = 4,2 cm
Vpiedra = π · 4,22 · 2,2 = 121,86 cm3
36
Con una barra cilíndrica de oro de 15 cm de larga y 5 mm de diámetro
se fabrica un hilo de 1/4 mm de diámetro.
¿Cuál es la longitud del hilo?
Radio del hilo = 1 mm = 0,125 mm
8
Radio de la barra = 2,5 mm
Largo de la barra = 15 cm = 150 mm
π · 2,52 · 150 = π · 0,1252 · l
(donde l es la longitud del hilo)
2
2,52 · 150 = 60 000 mm = 60 m
l = π · 2,5 · 150
=
π · 0,1252
0,1252
37
Un sótano cuya superficie es de 208 m2 se ha inundado. El agua llega a
1,65 m de altura. Se extrae el agua con una bomba que saca 6 hl por minuto.
¿Cuánto tiempo tardará en vaciarlo?
Volumen de agua = 208 · 1,65 = 342,2 m3 = 3 422 hl
3 422 : 6 = 572 minutos = 9 h 32 min
La bomba tardará en vaciar el sótano 9 h 32 min.
38
Una pared debe tener 7,5 m × 5,6 m y un grosor de 30 cm.
¿Cuántos ladrillos de 15 cm × 10 cm × 6 cm serán necesarios si en su construcción el cemento ocupa un 15% del volumen?
Volumen de la pared = 7,5 · 5,6 · 0,3 = 12,6 m3
Volumen de la pared sin cemento = 12,6 · 0,85 = 10,71 m3
Unidad 12. Medida del volumen
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 11
Volumen de un ladrillo = 0,15 · 0,1 · 0,06 = 0,0009 m3
10,71
Número de ladrillos = = 11 900
0,0009
39
Una columna de basalto tiene forma de prisma hexagonal regular. El lado de la base mide 15 cm. La altura de la columna es de 2,95 m.
Halla su peso sabiendo que 1 m3 de basalto pesa 2 845 kg.
a
h
l
l = 15 cm
h = 2,95 m
a = √152 – 7,52 = 13 cm
Abase = 6 · 15 · 13 = 585 cm2
2
Volumen = 585 · 295 = 172 575 cm3 = 0,172575 m3
Peso = 0,172575 · 2 845 = 491 kg
PÁGINA 241
40
La base de una pirámide regular es un hexágono de 15 cm de lado. Su altura es de 30 cm. Halla su
volumen.
Partimos esta pirámide por un plano paralelo a la
base que corta a la altura en la mitad.
Halla el volumen de cada una de las dos partes resultantes.
• Volumen de la pirámide entera:
a = √152 – 7,52 = 13 cm
Volumen = 1 · 6 · 15 · 13 · 30 = 5 850 cm3
3
2
• Volumen de la pirámide y del tronco de pirámide resultantes:
La base de la pirámide inicial y la base de la pirámide pequeña generada por
el plano son semejantes (método de proyecciones). Por tanto, sus lados serán
proporcionales.
Unidad 12. Medida del volumen
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 12
30
La pirámide pequeña será una pirámide de altura cm, lado de la base
2
15
13
cm y apotema cm.
2
2
Volumen de la pirámide pequeña:
1 · 6 · 15/2 · 13/2 · 30 = 5 850 = 731,25 cm3
3
2
2
8
Volumen del tronco de cono = 5 850 – 731,25 = 5118,75 cm3
41
Para medir el volumen de una piedra más grande
que la del ejercicio 35, depositamos el mismo recipiente
lleno de agua dentro de una gran fuente cilíndrica vacía.
Echamos la piedra dentro de la vasija y el agua derramada sube 2,3 cm.
Halla el volumen de esta otra piedra sabiendo que el diámetro interior de la fuente es de 24 cm.
Diámetro exterior de la vasija = 9 cm → radio = 4,5 cm
Diámetro interior de la fuente = 24 cm → radio = 12 cm
Volumen de la base (diferencia de círculos) = π · 122 – π · 4,52 = 388,6 cm2
Volumen del agua = 388,6 · 2,3 = 893,78 cm3
El volumen de la piedra es de 893,78 cm3.
PROBLEMAS DE ESTRATEGIA
42
80 000 l
50 000 l
30 000 l
Unidad 12. Medida del volumen
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 13
Luis, Lucio y Leo quieren regar sus campos con el agua del depósito grande
(los otros dos están vacíos). Han acordado que Luis se llevará el 50%, Lucio
el 25% y Leo el resto. Por supuesto, tienen bombas para trasegar agua, pero
no disponen de medidas. Solo saben la capacidad de los tres depósitos. ¿Cómo lo harán?
En el momento que se sepa la cantidad que corresponde a alguno de ellos, esta puede verterse al campo correspondiente.
Luis se llevará el 50% → 40 000 l
Lucio se llevará el 25% → 20 000 l
Leo se llevará el 25% → 20 000 l
Llamamos A al depósito de 30 000 l, B al de 50 000 l y C al de 80 000 l.
Se trasvasan 50 000 l del depósito C al B y, a continuación, 30 000 l del B
al A. Así, tendrán 20 000 l en B, con los que puede regar, por ejemplo, Lucio.
Ahora tienen 30 000 l en C y 30 000 en A. Se pasan los 30 000 l de A a B
y 20 000 l de C a B. Ahora en A no hay nada, en B hay 50000 l y en C
hay 10 000 l.
Se pasan 30 000 litros de B a A, con lo que vuelven a tener 20 000 l en B,
los que le corresponden a Leo.
Y luis ya tiene sus 40 000 litros, los 30 000 de A y los 10 000 de C.
43 ¿Qué porción de la caja ocupa cada uno de los siguientes tetraedros?
Para formar el tetraedro marcado en la caja cúbica, hay que eliminar del cubo
estos cuatro cuerpos marcados en rojo:
Unidad 12. Medida del volumen
12
SOLUCIONES A LOS EJERCICIOS
DE LA UNIDAD
Pág. 14
Cada uno de ellos es una pirámide de base triangular.
a2
Si el cubo tiene arista a, la base de la pirámide tiene área y su altura es a.
2
Su volumen, por tanto, es:
2
Vpirámide = 1 · a · a = 1 a 3
3 2
6
El volumen del tetraedro será entonces:
Vtetraedro = a 3 – 4 · 1 a 3 = a 3 – 2 a 3 = 1 a 3
6
3
3
1
Es decir, del volumen de la caja cúbica.
3
Unidad 12. Medida del volumen