Compuertas Lógicas

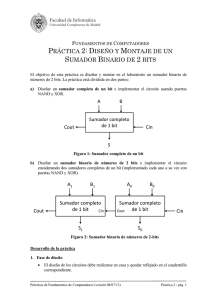
Compuertas Lógicas
M. en C. Erika Vilches
Parte 2
Compuerta OR
• Tiene dos o más entradas y una sola salida.
• Produce una salida ALTA cuando cualquiera
de las entradas es ALTA. La salida es BAJA
solamente cuando todas las entradas son
BAJAS.
• Una compuerta OR determina cuando una o
mas de sus entradas son ALTAS y produce
una salida ALTA para indicar esta condición.
Los 4 casos posibles para dos entradas
Tabla de verdad para la compuerta OR
Operación con ondas de entrada
Expresiones Lógicas
para una compuerta OR
• La función lógica OR de dos variables se
representa matemáticamente por un + entre
las dos variables, A+B
• Las reglas básicas de la suma en álgebra
booleana son:
• La suma booleana es lo mismo que la
función OR
• Tenga en cuenta que la suma booleana
difiere de la suma binaria en el caso donde
dos 1s se suman.
• No hay carry en una suma booleana.
• La operación de una compuerta OR de dos
entradas puede expresarse:
Ejemplo de Aplicación
Circuito de detección de intrusos simplificado
Compuerta XOR
• Tiene solo 2 entradas.
• La salida es ALTA solo cuando ambas
entradas se encuentran en niveles lógicos
opuestos.
Las 4 posibilidades de la compuerta XOR
Tabla de verdad para la compuerta XOR
Circuito para detectar una falla en dos
circuitos idénticos trabajando en paralelo
Medio Sumador
•
Reglas básicas de la suma →
•
Estas operaciones son llevas a cabo por un
circuito llamado medio sumador.
•
Acepta dos dígitos binarios en las entradas y
produce dos digitos binarios en sus salidas, un
bit con la suma y un bit para el carry.
Lógica del Medio
Sumador
• El carry de salida (Cout) es 1 solamente
cuando A y B son 1s, por lo tanto Cout se
puede expresar como el AND de las
variables de entrada →
• La salida con la suma es 1 solo cuando las
variables de entrada A y B no son iguales,
por lo tanto la suma se puede expresar
como el XOR de las variables de
entrada →
Tabla de verdad para un medio sumador
De las ecuaciones del medio sumador,
podemos obtener su implementación lógica
Sumador Completo
• Acepta dos bits de entrada y un carry.
Genera una suma de salida y un carry de
salida.
• Acepta un carry de entrada (Cin), a
diferencia del medio sumador
Símbolo lógico para el sumador completo
Tabla de verdad para el sumador completo
Lógica del Sumador
Completo
• De el medio sumador, sabemos que la suma
de las entradas A y B es el XOR de esas
variables.
• Para sumar el Cin a los bits de entrada, se
debe XORear con
ecuación →
, llegando a la
• El Cout es 1 cuando ambas entradas del
primer XOR son 1s, o cuando ambas
entradas del segundo XOR son 1s (estudiar
la tabla)
• Por lo tanto Cout se produce con las
entradas A ANDeada con B y A XOR B
ANDeado con Cin. Estos dos términos se
ORean, para dar →
+
=
Dos medios sumadores
≡
Un sumador completo
≡
Un sumador completo
Un sumador completo
Sumadores Binarios
Paralelos
• Un sumados completo es capaz de 2
números de 1 bit y un carry.
• Para sumar números binarios de más de 1
bit, se utilizan sumadores completos
adicionales.
• Se requiere un sumador completo por bit.
Por lo tanto para 2 bits se necesitan 2
sumadores, para 4 bits, 4 sumadores, etc.
Sumadores Paralelos de
4 bits
¿Qué hacer para 8 bits?
Utilizar 2 sumadores de 4 bits
(Cout → Cin)
Ejemplo de Aplicación
Sumador y restador en complemento a dos
para números binarios de 4 bits con detección
de overflow