TEMA 3: POLINOMIOS Y FRACCIONES ALGEBRAICAS

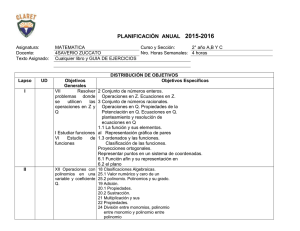
TEMA 3: POLINOMIOS Y FRACCIONES ALGEBRAICAS
CONCEPTOS:
.- Lenguaje algebraico: es la combinación de números, letras y símbolos
matemáticos utilizados para expresar algo de forma matemática. (es el idioma de las
matemáticas).
.- Expresión algebraica: es una combinación de nºs y letras relacionados entre
sí por las operaciones aritméticas.
Monomio: expresión algebraica con un solo término.
Binomio: expresión algebraica con dos términos.
Polinomio: expresión algebraica con varios términos.
Coeficiente (parte numérica; el número)
parte literal (las letras con sus
exponentes)
4xy + 5z + 3xyz2 – 15
Termino independiente
Término (cada uno de los sumandos de una expresión algebraica;
conjunto de número y letras entre signos de suma o resta)
Grado: es la mayor de las sumas de los exponentes de las partes literales de los
terminos
.- Valor numérico de una expresión algebraica: es el valor que nos da al
sustituir las letras por un valor determinado y realizar las operaciones que indica la
expresión.
Para x = 1
Y=2
Z=3
4xy + 5z + 3xyz = 4 · 1 · 2 + 5 · 3 + 3 · 1 · 2 · 3 = 8 + 15 + 18=41
.- Expresiones algebraicas semejantes o términos semejantes: son aquellas/os
que tienen la misma parte literal.
34ax es semejante a 5ax
23xz también es semejante a 4zx (orden de los factores no altera el producto).
4ab2 no es semejante a 5ab.
OPERACIONES CON EXPRESIONES ALGEBRAICAS:
.- Suma y resta de expresiones algebraicas:
(para sumar o restar expresiones algebraicas es necesario que sean semejantes)
- se suman o restan coeficientes y se deja la misma parte literal.
- Si no son semejantes todos los términos se suman o restan los
semejantes entre ellos.
4x2 + 7x2 + 3x2 = 14x2
/
8ab + 3b -5ab + 4b + 5a = 3ab + 7b + 5a
.- Multiplicación y división de monomios:
- se multiplican/dividen los coeficientes.
- Se multiplican/dividen las partes literales.
4·5=20
4z2y · 5z3y5 = 20 z5y6
/
25x5y2z : 5x3y = 5x2yz
z2·z3 = z5
y·y5 = y6
.- Multiplicación de polinomios: el producto de dos polinomios es otro
polinomio cuyos términos se obtienen multiplicando cada termino del 1º por cada uno
de los términos del 2º, y sumando luego los que resulten semejantes. Ej:
8x
2


 5 · 2x 2  x  3  8x 2 ·2x 2  8x 2 ·x  8x 2 ·3  5·2x 2  5·x  5·3  16x 4  8x 3  24x 2 
 10x 2  5x  15  16x 4  8x 3  14x 2  5x  15
Potencia de polinomios: para elevar un polinomio a una potencia, debe
multiplicarse por si mismo tantas veces como indique el exponente.
Identidades notables: son productos y potencias de binomios que, por
su utilidad e interés, se estudian de forma individual:
cuadrado de una suma: (a + b)2 = a2 + b2 + 2ab
cuadrado de una diferencia: (a –b)2 = a2 + b2 - 2ab
suma por diferencia: (a +b) (a-b) = a2 – b2
cubo de una suma: (a + b)3 = a3 + 3a2b + 3ab2 + b3
cubo de una diferencia: (a – b)3 = a3 -3a2b + 3ab2 – b3
.- División de polinomios:
Algoritmo:
1º.- Escribimos dividendo y divisor ordenados, dejando hueco si el dividendo
está incompleto.
2º.- Dividimos el primer monomio del dividendo entre el primero del divisor,
obteniendo así el primer monomio del cociente.
3º.- Multiplicamos el monomio del cociente por el divisor y el resultado lo
restamos del dividendo.
4º.- Repetimos el proceso hasta obtener un resto de grado inferior al divisor.
3x4
+ 5x2 - 2x + 6 x2 + 2x
-3x4-6x3
-6x3 + 5x2
3x2 – 6x + 17
6x3 +12x2
17x2 - 2x
-17x2 – 34x
-36x + 6
La división de polinomios cumple la propiedad fundamental de la división:
D(x) = d(x) · c(x) + r(x)
Regla de Ruffini: nos permite realizar de un modo sencillo cualquier división
de polinomios cuyo divisor es del tipo x – a ó x + a.
1º.- Escribimos los coeficientes del dividendo ordenados, dejando hueco o
escribiendo 0 si falta algún termino. A su izquierda escribimos el valor de a. (si el
divisor es del tipo x+a, debemos tener en cuenta que el valor de a es negativo).
2º.- Bajamos el primer coeficiente del dividendo.
3º.- Multiplicamos a por dicho coeficiente, y el resultado lo escribimos para
sumarlo con el coeficiente siguiente, y así sucesivamente.
4º.- Los nºs que hemos hallado son los coeficientes del cociente, el último de
ellos es el resto de la división. Para obtener el cociente, añadimos la indeterminada x,
rebajando en uno el grado del dividendo.
Ej: (3x4 + 5x2 – 2x + 6) : (x – 2)
3
0
5
-2
6
2
3
6
6
12
17
Cociente: 3x3 + 6x2 + 17x + 32
34
32
64
70
Resto: 70.
Teorema del resto: al dividir un polinomio P(x), entre un binomio del tipo
x-a, el resto de la división es igual al valor numérico del polinomio para x=a.
En el ej. anterior: P(2) = 3·24+5·22-2·2+6= 48+20-4+6 =70
.- Factorización de polinomios:
Teorema del factor: un polinomio P(x) tiene como factor x – a si el valor
numérico de dicho polinomio para x = a es 0.
Un polinomio tendrá tantos factores del tipo x – a como valores de a determinen
que P(a) = 0.
Raíces de un polinomio: son las soluciones de la ecuación polinómica P(x) = 0.
Es el nº a que, sustituido en lugar de la x, hace que el valor numérico del polinomio sea
igual a cero.
Las raíces enteras de un polinomio, si existen, se encuentran entre los
divisores del término independiente.
Ej: si P(x) = x3 – 2x2 – 5x + 6 => las posibles raíces enteras son  1,  2,  3,
 6. Habrá que buscar cuál de ellas anulan el polinomio.
Un polinomio de grado n podrá tener como máximo n raíces reales
(Teorema fundamental del algebra).
Factorización: Si un polinomio P(x) de grado n tiene n raíces r1 , r2 , r3 ,...,rn , y a es el
coeficiente del termino principal, puede factorizarse como:
P(x) = a (x- r1 ) · (x- r2 ) · … · (x- rn )
Los polinomios que no se pueden factorizar se llaman irreducibles.
Descomposición factorial de un polinomio: para llegar a la factorización de un
polinomio existen diversa estrategias a realizar durante la descomposición que se
complementan entre sí.
1.- sacar factor común, sólo cuando el polinomio no tiene término
independiente.
2.- aplicar el teorema del factor, comprobando el valor numérico del
polinomio para las posibles raíces y utilizando la regla de Ruffini.
3.- resolver ecuaciones de 2º grado.
4.- utilizar las identidades notables.
5.- etc.
.- M.C.D. y m.c.m. de polinomios: para hallar el M.C.D. y el m.c.m. de
polinomios se aplica el mismo procedimiento que se emplea para los nºs.
1.- Se factorizan los polinomios.
2.- el M.C.D. se calcula multiplicando los factores comunes con el
menor exponente con el que aparecen.
3.- el m.c.m. se multiplican los factores comunes y no comunes
elevados al mayor exponente con el que aparecen.
FRACCIONES ALGEBRAICAS:
Concepto: El conciente entre dos polinomios puede expresarse mediante una
P( x)
fracción algebraica:
Q ( x)
Los conceptos y contenidos relacionados con las fracciones algebraicas siguen
pautas similares al de las fracciones de nºs enteros.
.- Dos fracciones algebraicas son equivalentes si tienen el mismo valor y se
cumple que el producto cruzado de sus términos da el mismo resultado. Se cumple:
A( x ) P ( x )
y
son equivalentes si A(x) · Q(x) =B(x) · P(x)
B ( x) Q ( x)
.- Se pueden simplificar si numerador y denominador posen factores comunes
en su factorización. Una fracción algebraica es irreducible si no se puede reducir a otra
equivalente con numerador y denominador de menor grado que la fracción original.
.- Suma y resta: se calcula el mcm de los denominadores y se buscan fracciones
equivalentes a las iniciales con igual denominador. por último se suman/restan los
numeradores y se simplifica si es posible.
.- Multiplicación: se multiplican los numeradores
simplificando factores si es posible.
y los denominadores,
.- División: Se multiplican el numerador de la 1º y el denominador de la 2º para
calcular el nuevo numerador y los dos restantes para calcular el denominador,
simplificando factores si es posible. (multiplicar en cruz).
.- Las potencias de fracciones algebraicas con exponente entero tienen las
mismas propiedades que las de las fracciones numéricas.
.- Las operaciones combinadas de fracciones algebraicas se rigen por la misma
jerarquía de operaciones que con el resto de conjuntos numéricos, siendo conveniente
simplificar tanto los resultados parciales como los finales siempre que se pueda.