Suma de fracciones

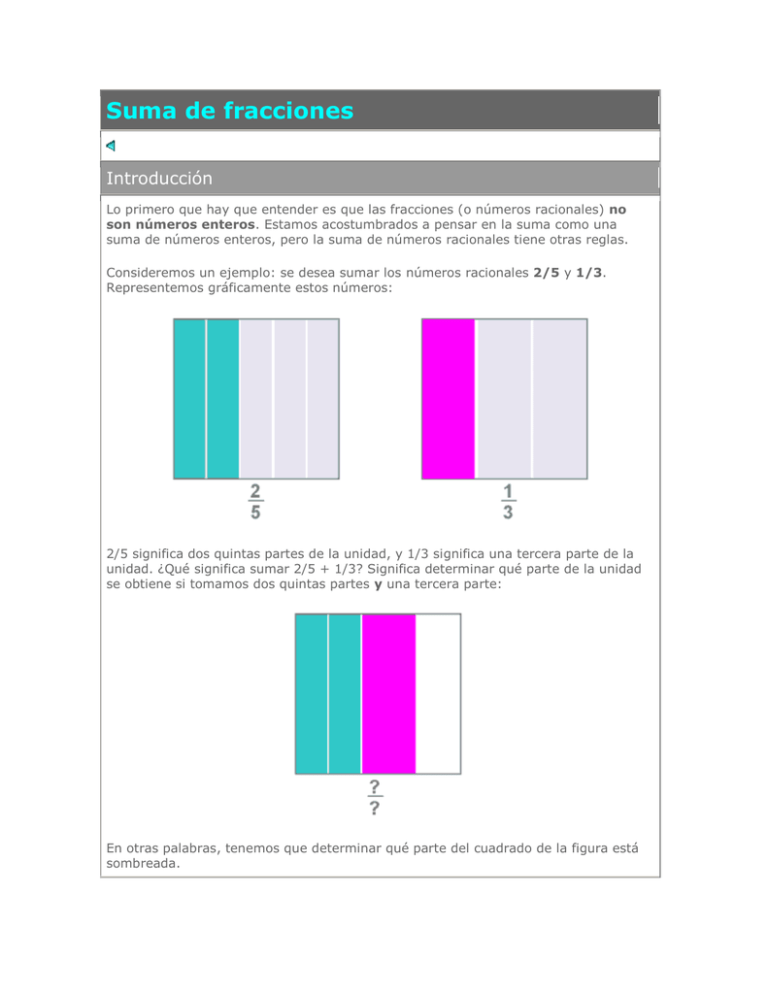
Suma de fracciones
Introducción
Lo primero que hay que entender es que las fracciones (o números racionales) no
son números enteros. Estamos acostumbrados a pensar en la suma como una
suma de números enteros, pero la suma de números racionales tiene otras reglas.
Consideremos un ejemplo: se desea sumar los números racionales 2/5 y 1/3.
Representemos gráficamente estos números:
2/5 significa dos quintas partes de la unidad, y 1/3 significa una tercera parte de la
unidad. ¿Qué significa sumar 2/5 + 1/3? Significa determinar qué parte de la unidad
se obtiene si tomamos dos quintas partes y una tercera parte:
En otras palabras, tenemos que determinar qué parte del cuadrado de la figura está
sombreada.
Cómo no sumar
Antes de proceder a explicar cómo se suma, observemos que no se pueden sumar
los numeradores y los denominadores por separado. El resultado de la suma
2/5 + 1/3 no es (2+1)/(5+3)=3/8. En efecto, la figura siguiente muestra que el
resultado de 2/5 + 1/3, sea lo que sea, es más que la mitad, mientras que 3/8 es
menos que la mitad; por lo tanto, no pueden ser iguales:
Cómo sumar
Una vez aclarado cómo no se suma, veamos cómo podríamos sumar 2/5 + 1/3.
La idea fundamental es dividir la unidad en "trozos" más pequeños de modo que cada
una de las fracciones que deseamos sumar contenga una cantidad entera de estos
trozos. En este caso, esto se logra dividiendo la unidad en 15 partes iguales:
Como se ve en la figura de la derecha, 2/5 es lo mismo que 6/15, y 1/3 es lo mismo
que 5/15. Por lo tanto, sumar 2/5 + 1/3 es lo mismo que sumar 6/15 + 5/15. Y esta
suma, por supuesto, es 11/15. Así hemos obtenido la respuesta al problema: 2/5 +
1/3 = 11/15.
¿Pero de dónde salió el 15? ¿Cómo sabíamos que teníamos que dividir la unidad en
15 partes, y no en 18, o en 57, o en otra cantidad? Bueno, tenemos que dividir la
unidad en trozos que "quepan justo" en 1/5 y en 1/3, y la forma más simple de
determinar de qué porte deben ser esos trozos es multiplicar los denominadores:
3x5=15. Observa que 1/15 es la tercera parte de un quinto, y es también la quinta
parte de un tercio, de modo que podemos dividir cada tercio en cinco quinceavos y
cada quinto en tres quinceavos.
En general, cuando se deban sumar fracciones de distinto denominador habrá que
aplicar el siguiente procedimiento:
a/b + c/d = (ad + bc)/bd
En el ejemplo, 2/5 + 1/3 = (2x3 + 1x5)/3x5 = (6 + 5)/15 = 11/15
El mínimo común denominador
De lo anterior podemos deducir lo siguiente: para sumar fracciones de distinto
denominador hay que convertirlas a otras fracciones equivalentes que tengan el
mismo denominador. Para ello debemos amplificar cada una de las fracciones por un
factor adecuado. La forma más simple de hacerlo es amplificar cada una de las
fracciones por el denominador de la otra:
2/5 + 1/3 = (2x3)/(5x3) + (1x5)/(3x5) = 6/15 + 5/15 = 11/15
Sin embargo, este método no es siempre el mejor. Por ejemplo, si quisiéramos sumar
1/5550 + 1/4550
este método nos obligaría a efectuar cálculos complicados (¡5550x4550=25252500!),
aumentando la posibilidad de error. Es por ello que se prefiere amplificar cada
fracción por el factor más pequeño posible que nos permita obtener
denominadores iguales. Veamos, por ejemplo, la suma
5/12 + 4/9
Podríamos amplificar la primera fracción por 9 y la segunda por 12, obteniendo:
5/12 + 4/9 = 45/108 + 48/108 = 93/108
Pero sería más eficiente amplificar la primera por 3 y la segunda por 4, y así
obtendríamos:
5/12 + 4/9 = 15/36 + 16/36 = 31/36
Además de facilitar los cálculos, este procedimiento nos entrega el resultado en la
forma más reducida (no es necesario simplificar, mientras que en el caso anterior el
resultado 93/108 se debe simplificar por 3 para obtener 31/36)
¿Cómo sabemos que se debe amplificar la primera por 3 y la segunda por 4?
Recordemos que el objetivo es convertir las fracciones en otras equivalentes que
tengan el mismo denominador, y además que ese denominador común sea el más
pequeño posible. En otras palabras, debemos hallar el mínimo común
denominador. Éste es simplemente el mínimo común múltiplo de los
denominadores. El mínimo común múltiplo de 12 y 9 es 36. Para obtener el
denominador 36 en la primera fracción debemos amplificarla por 3, y para obtener el
denominador 36 en la segunda fracción debemos amplificarla por 4.