RESUMEN DE CONTRASTES DE HIPBTESIS PARAMETRICOS.

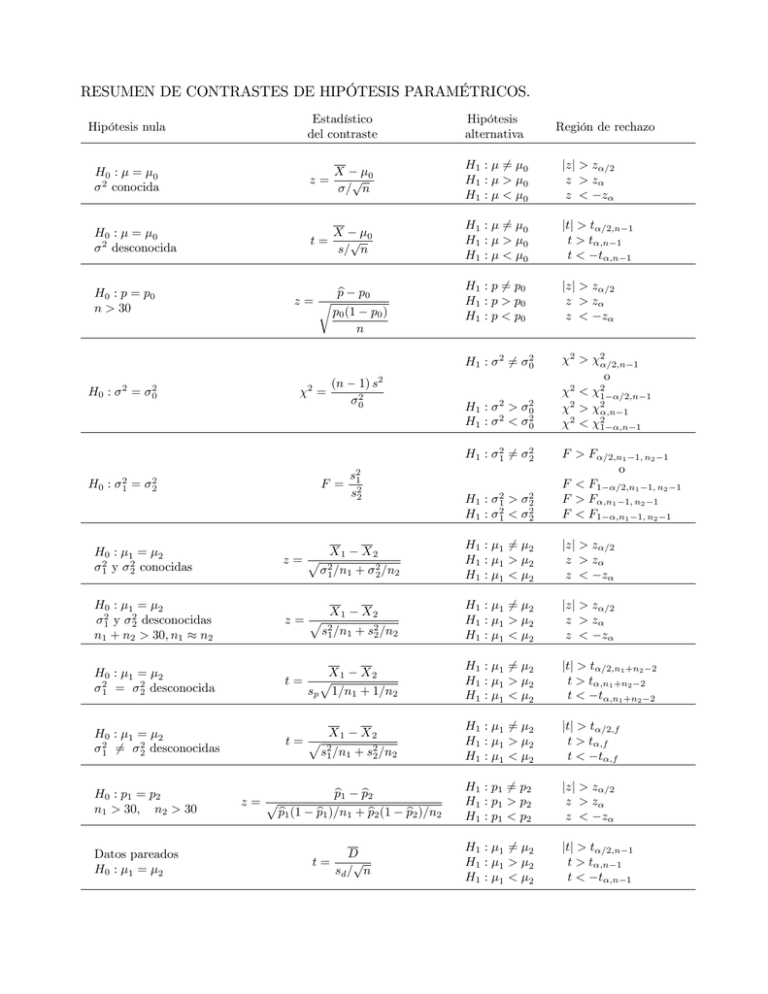
RESUMEN DE CONTRASTES DE HIPÓTESIS PARAMÉTRICOS.
Estadístico
del contraste
Hipótesis nula
H0 : = 0
2
conocida
X
z=
H0 : = 0
2
desconocida
0
= n
X
p 0
s= n
t=
H0 : p = p0
n > 30
p
Hipótesis
alternativa
z=r
pb
6=
>
<
H1 :
H1 :
H1 :
6=
>
<
p0 )
H0 :
H0 :
2
1 y
2
2
1
=
=
2
0
2
2
2
1 = 2
2
2 conocidas
H0 : 1 = 2
2
2
1 y 2 desconocidas
n1 + n2 > 30; n1 n2
t=
H0 : 1 = 2
2
2
1 6=
2 desconocidas
H 0 : p1 = p2
n1 > 30; n2 > 30
Datos pareados
H0 : 1 = 2
2 =n
1
1
2 =n
2
2
X1
H1 :
H1 :
H1 :
H1 :
H1 :
H1 :
X2
s21 =n1 + s22 =n2
z=p
pb1 (1
pb1
pb2
pb1 )=n1 + pb2 (1
t=
D
p
sd = n
2
1
H1 :
H1 :
H1 :
X
X2
p 1
sp 1=n1 + 1=n2
t= p
H1 :
H1 :
H1 :
H1 :
X2
+
H1 :
H1 :
2
H1 :
H1 :
X1 X2
z=p 2
s1 =n1 + s22 =n2
H0 : 1 = 2
2
2
1 =
2 desconocida
jtj > t =2;n
t > t ;n 1
t < t ;n
0
0
0
1
1
jzj > z =2
z >z
z < z
2
pb2 )=n2
2
2
1
2
1
1
1
1
1
1
1
1
1
1
1
1
1
>
2
6=
2
0
>
<
2
0
2
0
6=
2
2
F >F
>
<
2
2
2
2
o
F < F1 =2;n1 1; n2
F > F ;n1 1; n2 1
F < F1 ;n1 1; n2 1
6=
>
<
6=
>
<
6=
>
<
6=
>
<
=2;n 1
o
2
s21
s22
X1
z=p
0
1) s
2
0
F =
2
2
(n
=
0
n
H1 :
H0 :
jzj > z =2
z >z
z < z
0
H1 : p 6= p0
H1 : p > p 0
H1 : p < p 0
p0
p0 (1
H1 :
H1 :
H1 :
Región de rechazo
2
2
2
2
2
2
2
2
2
2
2
2
2
2
<
>
<
2
1
2
2
1
=2;n 1
;n 1
;n 1
=2;n1 1; n2 1
jzj > z =2
z >z
z < z
jzj > z =2
z >z
z < z
jtj > t =2;n1 +n2
t > t ;n1 +n2 2
t < t ;n1 +n2
jtj > t =2;f
t > t ;f
t < t ;f
H1 : p1 6= p2
H 1 : p1 > p 2
H 1 : p1 < p 2
jzj > z =2
z >z
z < z
H1 :
H1 :
H1 :
jtj > t =2;n
t > t ;n 1
t < t ;n
1
1
1
6=
>
<
2
2
2
1
1
2
2
1