aplicaciones de la función generadora de momentos

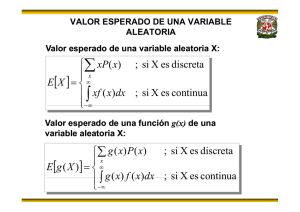
A P L I CA CI ONES DE LA FUN CI ÓN GENERA DOR A DE M OMEN TOS Andrés Camilo Ramírez Gaita [email protected] Trabajo de Grado para Optar por el Titulo de Matemático Director: Benigno Lozano Rojas Estadístico Universidad Nacional de Colombia Fundación Universitaria Konrad Lorenz Facultad de Matemáticas Bogotá D.C. 2007
1 AGRADECIMIENTOS Agradezco al profesor Benigno Lozano Rojas, quien me acompaño y apoyo con los valiosos aportes en la ejecución de este trabajo. También quiero agradecer al doctor Antonio Velasco muños decano de la facultad de matemáticas y a cada uno de los docentes y compañeros que tuvieron un aporte importante para mí formación a lo largo de la carrera.
2 RESUMEN Este documento consta de cuatro capítulos los cuales muestran la importancia de la función generadora de momentos y su aplicación a la hora de deducir la distribución de una o más variables aleatorias. Aunque existen tres técnicas para resolver dicho problema, la técnica de la función generadora de momentos es la mas sobresaliente, ya que además ayuda en el descubrimiento de variables aleatorias únicas y es muy útil cuando se trata de encontrar la distribución de sumas de variables aleatorias independientes, ayudando así en la demostración del teorema del límite central. This document is made up of four chapters which show the importance of the moment – generating – function and its use when deducing the distribution of one or more random variables. Eventhough there are three techniques to solve this problem, the moment – generating – function – technique is the most widely – used since it also helps in discovering the unique random variables and is very useful when trying to find the distribution of sums of independent random variables, helping in this way in the proof of the central – limit theorem.
3 CONTENIDO Página INTRODUCCION 1. 4 CONCEPTOS BASICOS 1.1. Variables aleatorias 5 1.2. Distribuciones de probabilidad 7 1.2.1. Distribución de probabilidad de variables discretas 1.2.2. Distribuciones de probabilidad de variables continúas 1.3. Valor esperado 2. 7 12 18 MOMENTOS Y FUNCIONES GENRADORAS DE MOMENTOS 2.1. Momentos 26 2.2. Función generadora de momentos 37 3. DISTRIBUCIÓN DE PROBABILIDAD DE UNA FUNCION DE UNA VARIABLE AL EATORIA 3.1. Técnica de la función acumulativa 45 3.2. Técnica de transformaciones 50 3.2.1. Técnica de transformaciones para variables discretas 50 3.2.2. Técnica de transformaciones para variables continuas 54 4. TECNICA DE LA FUNCION GENERADORA DE MOMENTOS 4.1. Descripción de la técnica 61 4.2. Distribución de sumas de variables aleatorias 67 APENDICE 74 CONCLUCIONES 85 BIBLIOGRAFIA 86
4 INTRODUCCIÓN En el área de la estadística es muy frecuente que el investigador no conozca como se comporta la distribución de probabilidad de su variable aleatoria. Para este hecho se han deducido los momentos, los cuales proporcionan una caracterización de la distribución de probabilidad. Muchas veces estos momentos suelen ser complicados para encontrarlos uno por uno, por esto si todos estos momentos existen, se pueden asociar a una función que los genere. Esta función toma el nombre de la función generadora de momentos. La función generadora de momentos no solo es usada en los momentos de una variable aleatoria. Frecuentemente en estadística se presenta la necesidad de deducir la distribución de probabilidad de una función de una o más variables. Es decir si se conoce la distribución de una variable aleatoria, y se tiene otra que es función de la anterior, se podría deducir la distribución de dicha variable. Este es uno de los campos donde la función generadora de momentos se aplica y es muy útil a la hora de deducir distribuciones de sumas de variables independientes. Para abordar este tema se ha creado este documento que consta de 4 capítulos, donde el lector podrá observar desde los conceptos básicos hasta la técnica de la función generadora de momentos. En el capitulo 1 se enunciarán temas básicos como, las variables aleatorias, distribuciones de probabilidad de una variable aleatoria y el valor esperado; el segundo se trataran a fondo temas como momentos y la función generadora de momentos, dejando claro así los concepto básicos para la aplicación de esta función ; en el tercer capítulo se abordaran 2 técnicas adicionales para deducir la probabilidad de una función de una o más variables aleatorias, y por último en el cuarto capítulo se presentará la tercera técnica llamada “técnica de función generadora de momentos” y su útil uso en la distribución de sumas de variables aleatorias.
5 CAPITULO UNO
CONCEPTOS BÁSICOS 1.1 Var iable aleator ia Definición 1.1: “Sea S un espacio muestral sobre el cual se encuentra definida una función de probabilidad. Sea X una función de valor real definida sobre S, de manera que transforme los resultados de S en puntos sobre la recta de los reales, se dice entonces que X es una variable aleatoria” 1 . El conjunto de valores que una variable aleatoria puede tomar se denomina el rango de la variable aleatoria. Se dice que X es una variable aleatoria si todos los resultados posibles de un espacio muestral, se pueden transformar en cantidades numéricas. Ejemplo 1.1: Supóngase el espacio muestral S en el que se consideran cada uno de los posibles resultados al lanzar tres monedas al aire: S = {ccc, ccs, csc, css, scc, scs, ssc, sss} donde c es cara y s es sello. Determinemos la variable X como el número de caras que hay en el espacio muestral, entonces a cada punto del espacio muestral se le asigna un valor numérico 0, 1, 2 o 3, estos pueden considerarse como valores que asume la variable aleatoria X , tal como lo muestra su grafica. 1 Probabilidad y estadística. George C.Canavos. Pág. 52
6 X (S) S R CCC 3 CCS CSC 2 SCC CSS 1 SCS SSC SSS 0
Gráfico 1.1 en este caso podemos observar que la variable aleatoria X toma el valor 1 para los elementos del conjunto E = {css, scs, ssc} Ì S. En si a cada elemento de espacio muestral, se le asigna un valor numérico. S X ccc 3 ccs 2 csc 2 scc 2 css 1 scs 1 ssc 1 sss 0 Tabla 1.1 Definición 1.2: “Se dice que una variable aleatoria X es discreta si su rango es un 2 conjunto finito o infinito numerable de valores”. Ejemplo 1.2: En el ejemplo 1.1 los valores posibles de una variable aleatoria discreta. 2 Probabilidad y estadística. George C.Canavos. Pág. 53 7 X son 0, 1, 2 y 3. Luego X es Definición 1.3: Se dice que una variable aleatoria X es continua si su rango es un conjunto infinito no numerable de valores. Este conjunto puede definirse en un intervalo o en un conjunto finito de intervalos. Ejemplo 1.3: Consideremos una variable aleatoria Y cuyos valores sean los pesos en kilogramos de todas las persona mayores de 20 años, lógicamente hay infinitos valores asociados a estos pesos. Si estos pesos se asignaran a la recta real, puede definirse un número infinito de valores para describir todos los posibles valores de peso. 1.2 Distr ibuciones de probabilidad Definición 1.4 una distribución de probabilidad es un listado de las probabilidades de todos los posibles resultados del espacio muestral que podrían obtenerse si el experimento se lleva a cabo. Las distribuciones de probabilidad se clasifican como discretas y continuas. 1.2.1 Distribuciones de probabilidad de var iables discretas Una variable aleatoria asume cada uno de sus resultados con cierta probabilidad. En el ejemplo 1.1 la variable aleatoria X que representa el número de caras al lanzar tres monedas al aire, tiene los siguientes valores posibles y con las respectivas probabilidades siguientes: Resultado Valor de la Numero de variable aleatoria ocurrencias ccc 3 1 1/8 ccs, csc, scc 2 3 3/8 ssc, scs, css 1 3 3/8 Sss 0 1 1/8 Tabla 1.2
8 probabilidad nótese que los valores posibles de X conforman los posibles conteos sobre el espacio muestral y en consecuencia las probabilidades suman 1. Para mayor comodidad es necesario usar una función con el objeto de representar las probabilidades de una variable aleatoria y se define por: f ( x ) = P ( X = x ) ; y se lee como “la probabilidad de que X tome el valor x ” esta función toma el nombre de función de probabilidad o distribución de probabilidad de la variable aleatoria discreta X , en el ejemplo 1.1 si se necesitara saber cual es la probabilidad de que salgan 2 caras en el mismo lanzamiento se usaria la función de probabilidad, donde x =2; entonces f ( 2 ) = P ( X = 2 ) = 3/8 ; Definición 1.5: “ Sea X una variable aleatoria discreta. Se llamará función de probabilidad de la variable aleatoria f ( x ) = P ( X = x ) X , si satisface las siguientes 3 propiedades” . 1. P ( x ) ³ 0; 2.
å x P ( x ) = 1; Ejemplo 1.4: Supóngase una variable aleatoria X que tiene como resultado dar el numero de caras menos el numero de sellos en 4 lanzamientos de una moneda. Encuentre la distribución de probabilidad para la variable aleatoria X . Solución: El espacio muestral se encuentra dado por: S = {cccc,cccs,ccsc,ccss,cscc,cscs,cssc,csss,sccc,sccs,scsc,scss,sscc,sscs,sssc,ssss} donde el número de ocurrencias es 16; 3 Probabilidad y estadística. George C.Canavos. Pág. 54
9 Resultado Valor de la Numero de probabilidad diferencia ocurrencias entre caras y sellos cccc 4 1 1/16 cccs,ccsc,cscc,sccc 2 4 4/16 ccss,cscs,cssc,sccs,scsc,sscc 0 6 6/16 csss,scss,sscs,sssc ­2 4 4/16 ssss ­4 1 1/16 Tabla 1.3 Ahora la distribución de probabilidades será: x ­4 ­2 0 2 4 f ( x ) 1/16 4/16 6/16 4/16 1/16 Tabla 1.4 Muchas veces necesitamos encontrar la probabilidad de que X sea menor o igual que x para este caso basta con observar que: P ( X £ x ) =…+ P ( X = 0 ) + P ( X = 1 ) +…+ P ( X = x ­1 ) + P ( X = x ) lo cual nos da una idea de sumar probabilidades o de acumularlas. Definición 1.6: “ La distribución acumulativa de la variable aleatoria probabilidad de que X sea menor o igual a un punto específico de x y esta dada por” 4 : F ( X ) = P ( X £ x ) =
f ( x i ) å
x x i £
Y además satisface las siguientes propiedades: 4 X es la Probabilidad y estadística. George C.Canavos. Pág. 54
10 1. 0 £ F ( x ) £ 1. 2. F ( x i ) £ F ( x j ) si xi £ x j . 3. p ( X > x ) = 1 ­ F ( x ) . 4. p ( X = x ) = F ( x ) - F ( x - 1 ) . 5. p ( x i < X £ x j ) = p ( X £ x j ) ­ p ( X £ x i ) = F ( x j ) - F ( x i ) . Cabe anotar que P ( X £ x ) ¹ P ( X < x ) si X es una variable discreta. P ( X £ x ) =…+ P ( X = 0 ) + P ( X = 1 ) +…+ P ( X = x ­1 ) + P ( X = x ) P ( X < x ) =…+ P ( X = 0 ) + P ( X = 1 ) +…+ P ( X = x ­1 ) Ejemplo 1.5: Encuentre la distribución acumulada de la variable aleatoria X del ejemplo 1.4 y usando las propiedades calcular: 1.
p ( X > 0 ) 2.
p ( X ³ 0 ) 3. P ( ­2 £ X £ 2 ) 4. P ( ­2 < X £ 2 ) 5. P ( ­2 £ X < 2 ) 6. P ( ­2 < X < 2 ) Solución: F ( ­4 ) = P ( X £ ­4 ) = P ( X = ­4 ) = 1/16; F ( ­2 ) = P ( X £ ­2 ) = P ( X = ­4 ) + P ( X = ­3 ) + P ( X = ­2 ) = 1/16 + 0 + 4/16 = 5/16; F ( 0 ) = P ( X £ 0 ) = P ( X = ­4 ) + P ( X = ­3 ) + P ( X = ­2 ) + P ( X = 0 ) = 1/16 + 4/16 + 6/16= 11/16; F ( 2 ) = P ( X £ 2 ) = P ( X = ­4 ) + P ( X = ­2 ) + P ( X = 0 ) + P ( X = 2 )
11 = 1/16 + 4/16 + 6/16 + 4/16 = 15/16; F ( 4 ) = P ( X £ 4 ) = P ( X = ­4 ) + P ( X = ­2 ) + P ( X = 0 ) + P ( X = 2 ) + P ( X = 4 ) = 1/16 + 4/16 + 6/16 + 4/16 + 1/16 = 1; Luego la distribución de probabilidades acumuladas es:
F ( X ) = x < -4
- 4 £ x < -2 - 2 £ x < 0 0 £ x < 2 2 £ x < 4 x ³ 4 ì 0 ï1 / 16 ï
ïï5 / 16 í
ï11 / 16 ï15 / 16 ï
ïî1 A continuación se muestran las graficas de f ( x ) y F ( x ) respectivamente f (X) FUNCIÓN DE PROBABILIDAD ­5 ­3 ­1 1 X Gráfico 1.2
12 3 5 FUNCIÓN DE DISTRIBUCIÓN ACUMULATIVA 15/16 F(x) 12/16 8/16 4/16 0 ­10 ­5 0 5 10 x Gráfico 1.3 1.
p ( X > 0 ) = 1 ­ F ( 0 ) = 1 – 11/16 = 5/16. 2.
p ( X ³ 0 ) = p ( X > 1 ) = 1 ­ F ( 1 ) = 1 – 11/16 = 5/16. 3. P ( ­2 < X £ 2 ) = F ( 2 ) ­ F ( ­2 ) = 15/16 – 5/16 = 10/16. 4. P ( ­2 £ X £ 2 ) = P ( ­3 < X £ 2 ) = F ( 2 ) ­ F ( ­3 ) = 15/16 ­1/16 = 14/16. 5. P ( ­2 £ X < 2 ) = P ( ­3 < X £ 1 ) = F ( 1 ) ­ F ( ­3 ) = 11/16 ­ 1/16 = 10/16. 6. P ( ­2 < X < 2 ) = P ( ­2 < X £ 1 ) = F ( 1 ) ­ F ( ­2 ) = 11/16 ­ 5/16 = 6/11 1.2.2 Distribuciones de probabilidad de var iables continuas En el caso de las distribuciones continuas p ( X = x ) = 0. Ejemplo 1.6: La variable aleatoria continua W se define como la altura de todas las personas mayores de 20 años en un intervalo de 170 hasta 180 centímetros. Supóngase que se quiere encontrar
p ( X = 175 ) , aparentemente parece que fuera sencillo calcularla, pero si entendiéramos que en el intervalo [170, 180] hay infinitos números, evidentemente hay infinidad de estaturas por lo cual
p ( X = 175 ) tiende a ser nulo, para este caso es mejor utilizar intervalos. Entonces para nuestro caso seria mejor encontrar p ( 174.9 £ X £ 175.1 ) .
13 La distribución de probabilidad de una variable continúa X esta caracterizada por una f ( x ) , la cual recibe el nombre de función de densidad de probabilidad y función proporciona un medio para calcular p ( a £ X £ b ) con b > a. De manera formal, la distribución de probabilidad de una variable aleatoria continua se define de la siguiente manera: Definición 1.7: “ Si existe una función · f ( x ) ³ 0 ·
ò · p ( a £ X £ b ) =
¥
-¥
f ( x ) tal que:” 5
­ ¥ < X < ¥
f ( x ) dx = 1
Entonces se dice que b òa f ( x ) dx a,b Î Â
f ( x ) es la función de densidad de probabilidad de la variable aleatoria continua X . De esta definición se derivan otras propiedades. 1. p ( X = a ) = 0 2. P (a £ X £ b ) = P (a< X ≤ b ) = P (a ≤ X < b) = P (a < X < b) Solución: a 1. p ( X = a ) = p ( a £ X £ a ) = ò f ( x ) dx = 0 2. p ( a £ X £ b ) = p ( X = a ) + p ( a < X < b ) + p ( X = b ) = p ( a < X < b ) a Para entender mejor el concepto de función de densidad, lo ilustraremos con un ejemplo. Ejemplo 1.7: Supóngase que se miden los tiempos entre 2 llamadas consecutivas, de 1000 clientes de una empresa que funciona de 7:00 AM a 5:00 PM y los agrupamos en intervalos de 1 hora. En la tabla 1.5 se enuncian el número de llamadas en cada intervalo y su respectiva frecuencia relativa. 5 Probabilidad y estadística. George C.Canavos. Pág. 58
14 Intervalo N° llamadas Frecuencia relativa 7 < x £ 8 20 0.020 8 < x £ 9 60 0.060 9 < x £ 10 100 0.100 10 < x £ 11 150 0.150 11 < x £ 12 170 0.170 12 < x £ 13 170 0.170 13 < x £ 14 150 0.150 14 < x £ 15 100 0.100 15 < x £ 16 60 0.060 16 < x £ 17 20 0.020 Tabla 1.5 Como se observa en la gráfica 1.3 la base de cada rectángulo tiene como longitud 1 y su altura es la frecuencia relativa, luego el área de cada rectángulo es su frecuencia relativa y por lo tanto la suma de sus áreas es 1. Supongamos ahora que los tiempos entre dos llamadas consecutivas se observan para 10000 y se agrupan en 20 intervalos de ½ hora, o también para 100000 en 40 intervalos de ¼ de hora, si aumentamos este proceso de aumentar el numero de observaciones y disminuir el tamaño de los intervalos, se llegara a una curva límite la cual toma el nombre de función de densidad de probabilidad para una variable aleatoria continua X , y se denota por f ( x ) ( grafico 1.4), evidentemente el área total bajo la curva es 1.
15 0,17 0,17 frecuencia relativa 0,15 0,15 0,1 0,1 0,06 0,06 0,02 7 0,02 8 9 10 11 12 13 14 15 16 x Gráfico 1.3 FUNCIÓN DE DENSIDAD 0,09 0,06 0,03 0 7,1 10,1 13,1 16,1 Gráfico 1.4 Al igual que las funciones de probabilidad de las variables aleatorias discretas tienen su función acumulativa, las variables aleatorias continuas también tienen su respectiva función acumulativa y se define como: F ( X ) = P ( X £ x ) =
x ò -¥
f ( t ) dt donde t es una variable artificial de integración.
16 La distribución F ( X ) es una función lisa no decreciente con las siguientes propiedades: 1. F ( ­ ¥ ) = 0 2. F ( ¥ ) = 1 3. p ( a < X < b ) = F ( b ) ­ F ( a ) 4. dF ( X ) = f ( x ) dx Ejemplo 1.8: Sea X una variable aleatoria continua definida por
2 ì
ï
4 ï
íp 1 + 2 x
ï
ïî0 f ( X ) = 1. probar que 2. Calcular
x ³ 2
en cuaquier otro caso f ( x ) es una función legítima de probabilidad. P ( X £ 4 3 / 3 ) , p ( 2 2 £ X £ 4 ) . 3. Encontrar F ( X ) , graficarla y usarla para encontrar los puntos dados Solución: 1. Al ser x > 0 no habrá problema con el radical y claramente se ve que f ( x ) ³ 0, ahora ò
¥
2
2 p 1 + 4 x
dx = 2
pò
1 ¥
2 1 + 2 Con lo que se concluye que 2.
P ( X £ 4 3 / 3 ) = 2
pò
4 dx =
2 æ 2 ö
ar cos ç ÷
p
è x ø
¥
2 =
2 ép
ù
- 0 ú = 1 ê
p ë 2 û
x 2 f ( x ) es una función legítima de probabilidad. 4 3 / 3 1 2 1 + 17 4 x 2 dx = 2
æ 2 ö
ar cos ç ÷
p
è x ø
4 3 / 3 2 =
2
x
2 p 1 + 4 1 4 2 2 =
ò
æ 3 ö 2 2 p ö 1 ÷ ­ ar cos (1 ) = æ ç ÷ = ÷
p è 6 ø 3 è 2 ø p
ar cos çç
pò
=
F ( x ) = p
2
P ( 2 2 £ X £ 4 ) = 2 p
1 + dx = 4 2
æ 2 ö
ar cos ç ÷
p
è x ø
4 2 2 x 2 æ 1 ö
è 2 ø
ar cos ç ÷ ­
2 p
æ 2 ö
÷
÷
2 è
ø
ar cos çç
2 æ p ö 2 æ p ö 2 1 1 ç ÷ ­ ç ÷ = ­ = p è 3 ø p è 4 ø 3 2 6 dt = 2
æ 2 ö
ar cos ç ÷
p
è t ø
x 2 t 2 =
2
æ 2 ö 2 æ 2 ö
ar cos ç ÷ ­ ar cos (1 ) = ar cos ç ÷
p
p
è x ø p
è x ø
2
Y la gráfica es: FUNCIÓN ACUMULATIVA 1 0,8 F(X) 3.
2 0,6 0,4 0,2 0 0 5 10 X Gráfico 1.4
18 15 20 P ( X £ 4 3 / 3 ) = F ( 4 3 / 3 ) =
2 p
p ( 2 2 £ X £ 4 ) = F ( 4 ) ­ F ( 2 2 ) =
=
æ 3 ö 2 æ p ö 1 ÷ = ç ÷ = ÷
è 2 ø p è 6 ø 3 ar cos çç
2 p
æ 1 ö
è 2 ø
ar cos ç ÷ ­
2 p
æ 2 ö
÷
÷
è 2 ø
ar cos çç
2 æ p ö 2 æ p ö 2 1 1 ç ÷ ­ ç ÷ = ­ = p è 3 ø p è 4 ø 3 2 6 1.3 Valor esperado Los grandes jugadores de poker dicen que los jugadores no experimentados pueden ganar dinero a corto plazo pero que perderán dinero a largo plazo. Lo contrario vale para profesionales y muy buenos jugadores, lo cuales ganarán generalmente a largo plazo. ¿Por qué esto es así? Esto se debe a un concepto conocido como “valor esperado”. Valor esperado es el beneficio que se espera. Por ejemplo, supóngase que se ha realizado una apuesta para lanzar una moneda. Si sale cara, se perderá $1, si sale cruz, se ganará $100. ¿Se debe aceptar teóricamente esta apuesta (asumiendo que la moneda es verdadera y existe un cincuenta­cincuenta de posibilidad de que salga cara o cruz? Obviamente, se debería aceptar la apuesta. Existe una probabilidad de 1/2 que caiga en cara y gane $100. Por lo tanto, la ganancia esperada es 0.5*$100=50. Si saliera cruz, se pierde $1. Por lo que, la perdida esperada 0.5*$1=0.50 Y el beneficio esperado es la ganancia esperada menos la pérdida esperada. Es decir, que el beneficio esperado es de $49,5. Obviamente, no se ganará $49,50. se Ganará $100 o se perderá $1. Sin embargo, debería verse la apuesta como "ganar" $49,50. Los resultados en los juegos de azar están influenciados por la suerte a corto plazo. Sin embargo, los resultados se verán cercanos a semejarse al valor esperado a largo plazo. Si se tira la moneda un millón de veces, el beneficio final será muy cercano a 49,50 millones.
19
Entonces resumiendo: X una variable discreta donde solo podrá tomar dos valores, $100(ganancia), $­1 (la perdida) o sea x = {­1, 100} ahora la probabilidad de ganancia es 0.5 y la ganancia Sea de perdida es 0.5. Por tanto su valor esperado es:
m = (­1) (0.5)+ (100) (0.5)=49.5 luego se observa que el valor esperado esta dado por:
1 E ( x ) = å x i . p ( x i ) = (­1) (0.5)+ (100) (0.5)=49.5 i = 0 Así se llega a la definición de valor esperado, media o esperanza matemática de una variable aleatoria Definición 1.8: La media de una variable aleatoria se considera como una cantidad numérica alrededor de la cual los valores de la variable aleatoria tienden a agruparse por lo tanto la media es una medida de tendencia central y se define por:
m = E ( x ) = å xp ( x ) Si X es una variable discreta
x ¥
m = E ( x ) = ò xf ( x ) dx X es una variable continua Si - ¥
En general definimos el valor esperado de una función de X , h ( X ) , por la igualdad
E[h ( x ) ] = å h ( x ) p ( x ) Si X es una variable discreta.
x ¥
E[h ( x ) ] = ò h( x ) f ( x ) dx Si X es una variable continua. - ¥
Análogamente para mas de dos variables X 1 , X 2 , X 3 ,..., X k el valor esperado de cualquier función h de las variantes, se define por
20 E [h ( x 1 , x 2 , x 3 ,..., x k ) ] = ååå ... å h ( x 1 , x 2 , x 3 ,..., x k ) p ( x 1 , x 2 , x 3 ,..., x k ) x 1 x 2 x 3 x k Si x1 , x 2 , x 3 ,..., x k variables discretas.
¥
E [h ( x 1 , x 2 , x 3 ,..., x k ) ] = ò h( x , x , x ,..., x k ) f ( x , x , x ,..., x k ) dx dx dx ... dx k 1 2 3 1 2 3 1 2 3 - ¥
Si x1 , x 2 , x 3 ,..., x k variables continúas. El valor esperado o media posee algunas propiedades: 1. E ( k ) = k para k una constante 2. E ( cx + k ) = cE ( x ) + k para 3. E[ g ( x ) + h ( x )] = E [( g ( x )] + E [( h ( x )] 4. E[ g ( x ) h ( x )] = E [( g ( x )] E [( h ( x )] k , c constantes NOTA: El valor esperado, puede no existir dependiendo si la correspondiente suma o integral diverge a un valor infinito. Ejemplo 1.9: Encontrar la media o valor esperado de la distribución de Poisson Solución: la distribución de Poisson esta dada por
ìe - l lx
ï
f ( x ) = í x ! ï0 î
x = 0, 1 , 2 , ... en cualquier otro valor luego ¥
e - l lx lx -1 -l
E ( x ) = å x . p ( x ) = å x. = le å
x ! )! x =0 x =0 x =1 ( x - 1 ¥
¥
ahora si hacemos y = x ­1, se tendría 0 £
y £ ¥ , y por tanto
21
l y -l l
= l e e = l
y = 0 ( y )! ¥
E ( x ) = le - l å
Ejemplo 1.10: Encontrar la media o valor esperado de la distribución binomial. Solución: La distribución binomial esta dada por:
ì n! p x ( 1 - p ) n - x ï
í( n - x )! x ! ï0 î
f ( x ) = x = 0 , 1 , 2 , ... , n 0 £ p £ 1 , n Î Z +
en cualquier otro valor entonces n
E ( x ) =
n
å x. P ( x ) =
x = 0 n ! x p x ( 1 - p ) n x å
( n - x )! x ! x -
= 0 n -1 =
( n - 1 )! p x ( 1 - p ) n - x ( n x )! ( x 1 )! x =1 n å
n -1 ( n - 1 )! p x å
) - ( x - 1 )]! ( x - 1 )! x [( n - 1 = np ( 1 - p ) ( n -1 ) -( x -1 ) -1 =1 Ahora si y = x - 1 , m = n - 1 se tendría 0 £ y £ m , y por tanto m m ! p y ( 1 - p ) ( m - y ) = np ( m y )! ( y )! y = 0 E ( x ) = np å
Es bueno recordar para los ejemplos 1.11 1.12 1.13 la función Gamma y la función Beta 1. La función Gamma esta definida por:
22 ¥
G ( n ) = ò u n -1 e -u du = ( n - 1 )! n > 0 0 y sus propiedades son:
· G ( n + 1 ) = n ! · G (n
+ 1 ) = n G ( n ) ·
G ( 1 / 2 ) = p
2. La función Beta esta definida por. 1 B( a , b ) = ò xa -1 ( 1 - x ) b -1 dx a , b > 0 0 £ x £ 1 0 La función Beta y la función Gamma se encuentran relacionadas por G (a ) G( b ) B (a , b ) = G ( a + b ) Nota: En el apéndice al final de este documento se muestran las deducciones anteriores y sus respectivas propiedades. Ejemplo 1.11: Encontrar la media o valor esperado de la distribución Gama Solución: La distribución Gamma esta dada por - x ì 1 a - 1 q
ï
x e f ( x ; a , q ) = í G( a ) q a
ï
0 î
x > 0, a, q > 0 , en cualquier otro valor entonces E ( x ) =
ò
¥
0 xf ( x ) dx =
ò
¥
0 -x
x x a -1 e q
a
G (a
) q
dx =
1 G ( a ) q a
ò
¥
0 -x
x a e q
dx ahora si observamos la integral podría transformarse en una función Gamma Sea u =
x 1
Þ du = dx Þ dx = qdu q q 23 a
æ x ö
u = ç ÷ Þ xa = u a q a
èq ø
a
luego 1 G ( a ) q a
E ( x ) =
ò
¥
0 u a q a e -uq du =
q ¥ a -u
u e du G (a
) ò0 q ¥ ( a +1 ) -1 -u
qG(a + 1 ) qaG(a ) u e dx = = = qa
ò
0 G (a
) G( a ) G( a ) =
Ejemplo 1.12: mostrar que la media de de la distribución Beta es:
a
a +b
Solución: La distribución Beta se encuentra definida por: ì G( a + b ) a - 1
x ( 1 - x ) b -1 ï
f ( x ; a , q ) = í G( a ) G( b ) ïî
0 0 £ x £ 1 a, q > 0 , en cualquier otro valor entonces E ( x ) =
1 1 0 0 G (a
+ b ) a
ò xf ( x ) dx = ò G( a ) G( b ) x
( 1 - x ) b -1 dx =
G (a
+ b ) 1 a
x ( 1 - x ) b -1 dx ò
0 G ( a ) G ( b ) = G(a + b ) G(a + b ) G( a + 1 ) G ( b ) B( a + 1 , b ) = G ( a ) G( b ) G ( a ) G ( b ) G ( a + b + 1 ) = G (a + b ) aG ( a ) a
= G( a ) ( a + b ) G ( a + b ) (a + b ) Ejemplo 1.13 Supóngase que la variable aleatoria Y representa el intervalo de tiempo entre dos llegadas consecutivas a una tienda y que su función de distribución esta dada por:
24
f ( y ) =
ì1 - 4y ï e í 4 ï0 î
y > 0, en cualquier otro valor Si las ganancias de dinero es igual a al cubo del tiempo entre dos llegadas, encontrar el valor esperado de las ganancias. Solución: El valor esperado de las ganancias, es encontrar E ( Y 3 ) , luego y 1 1 3 - 4 y e dy 4 ò0 1 E ( y 3 ) =
3 ò y f ( y ) dy =
0 Ahora si hacemos u=
y 1
Þ du =
dy Þ dy = 4du 4 4 3 æ y ö
u = ç ÷ Þ y3 = 64 u 3 è4ø
3 Entonces 1 E ( y 3 ) = 64 ò u 3 e - u du = 64 G (4 ) = 64(3!) = 384 0 Ejemplo 1.14 Encontrar el valor esperado de la distribución de Cauchy en el caso a = 0 y b = 1 . Solución: La distribución de Cauchy con a = 0 y b = 1 se encuentra definida por: f ( x ; 0,1) =
ì 1 ï
2 íp ( 1 + x ) ï0 î
x > 0
en cualquier otro valor 25 E ( X ) =
ò
¥
0 xf ( x ) dx =
=
ò
¥
0 x
1 1 ¥ x
dx = ò
dx 2 p ( 1 + x ) p 0 ( 1 + x 2 ) 1 ln( 1 + x 2 ) 2 p
¥
0 Lo cual indica que a medida de que x crezca E ( x ) también va a crecer o sea que la integral diverge, por tanto el valor esperado de la distribución no existe.
26 CAPITULO DOS MOMENTOS Y FUNCIONES GENERADORAS DE MOMENTOS 2.1 Momentos Los momentos de una variable aleatoria funciones de X son los valores esperados de ciertas x . Ellos forman una colección de medidas descriptivas que pueden ayudar a caracterizar la distribución de probabilidad X y verificar si todos los momentos son conocidos. Generalmente estos momentos se definen alrededor de 0 o del valor esperado. Definición 2.1: “ sea X una variable aleatoria. El r­ésimo momento de X alrededor de 0 se define por:” 6
m r ' ìå x r p ( x ) ïï x r = E ( x ) = í ¥
ï ò x r f ( x ) dx ïî- ¥
en el primer momento alrededor de 0 ( r = 1 ) para 6 Probalidad y estadística. George C.Canavos. Pág. 67
27 donde x es discreta donde x es continua X una variable discreta. m1' = E ( x 1 ) = E ( x ) Lo cual indica que es el conocido valor esperado o media, similarmente se tiene este valor si X fuese una variable continua. Definición 2.2: “ Sea X una variable aleatoria. El r­ésimo momento central de X (también conocido como el r­eximo momento alrededor de la media) se define por:” 7
m r ìå( x - m ) r p ( x ) ïï x r = E [( x - m ) ] = í ¥
ï ò ( x - m ) r f ( x ) dx ïî- ¥
donde x es discreta donde x es continua El momento central cero de cualquier variable aleatoria es 1. m 0 = E [( x - m ) 0 ] = E [1] = 1 El primer momento central de cualquier variable aleatoria es 0 m1 = E [( x - m ) 1 ] = E [x - m ] = E ( x ) - E ( m ) = m - m = 0 El segundo momento alrededor de la media es la varianza que se denota por var( X ) m 2 = var( X ) = E [( x - m ) 2 ] = E ( x 2 - 2 x m + m 2 ) = E ( x 2 ) - 2 mE ( x ) + m 2 = m 2 ' - 2 mm + m 2 = m 2' - m 2 La varianza de cualquier variable aleatoria es la diferencia del segundo momento alrededor de 0 y el cuadrado de la media o valor esperado. Generalmente se denota s 2 aunque a veces será conveniente denotarla por var( X ) . La varianza de una variable aleatoria es la medida de la dispersión de la distribución de probabilidad de esta. Por ejemplo, en el caso continuo si la mayor parte del área por debajo de la curva 7 Probalidad y estadística. George C.Canavos. Pág. 67
28 de distribución se encuentra cercana a la media, la varianza es pequeña o si por el contrario la mayor parte del área se encuentra muy dispersa de la media la varianza será grande. La raíz cuadrada de la varianza recibe el nombre de desviación estándar y se denota por s . La varianza al igual que el valor esperado tiene propiedades, así: Dadas dos constantes a y b.
· var(aX
+ b ) = a 2 var( X ) · var(aX
+ bY ) = a 2 var( X ) + b 2 var( Y ) + 2 cov( X , Y ) X y Y sean estadísticamente independientes
en al caso en que · var(aX
+ bY ) = a 2 var( X ) + b 2 var( Y ) Como se ha podido observar el segundo momento alrededor de la media se expresó en términos de los primeros dos momentos alrededor de 0. En general todos los momentos centrales de una variable se pueden expresar en términos de los momentos alrededor de 0, dado que: m r = E [( x - m ) r ]
Recuerdese que
æ n ö
n
( a + b ) n =
çç ÷÷a n i b i å
i i = 0 -
è ø
O sea que:
r
( x - m ) r =
æ r ö
(- 1 )i çç ÷÷ x r i m i å
i i = 0 -
è ø
ahora
é r ù
æ r ö
m r = E êå (- 1)i çç ÷÷ x r -i m i ú = è i ø
ë i =0 û
r
r r
r (- 1)i æçç ö÷÷ m i E ( x r -i ) = å æçç ö÷÷(- m ) i m r ' -i å
i = 0 i = 0 è i ø
è i ø
ejemplo si se necesitara el tercer momento central 3 m 3 = æ 3 ö
çç ÷÷( - m ) i m
å
i
i = 0 è ø
' 3 -i æ 3ö
æ 3 ö
æ 3 ö
æ 3 ö
= çç ÷÷( - m ) 0 m 3 ' + çç ÷÷( - m ) m 2 ' + çç ÷÷( - m ) 2 m1 ' + çç ÷÷( - m ) 3 m 0 ' è 0 ø
è 1 ø
è 2 ø
è 3 ø
= m 3 ' - 3mm 2 ' + 3 m 2 m 1 ' - m 3 = m 3 ' - 3mm 2 ' + 3 m 3 - m 3 29 = m 3 ' - 3mm 2 ' + 2 m 3 Los momentos centrales tercero y cuarto proporcionan información muy útil con respecto a la forma de la distribución de probabilidad de X y reciben el nombre de factores de forma. El tercer momento de cualquier variable aleatoria se encuentra relacionado con la asimetría de la distribución de probabilidad de X . En el caso en que las distribuciones de probabilidad presenten más de un pico, el tercer momento puede presentar datos erróneos, por eso es conveniente usar el tercer momento estandarizado, dado por: a 3 = m 3 /( m 2 ) 3 / 2 = m 3 / var( X ) 3 / 2 a 3 recibe el nombre de coeficiente de asimetría y como su nombre lo indica mide la asimetría de la distribución de probabilidad con respecto a su dispersión. La distribución puede ser:
·
Asimétrica positivamente a 3 > 0 0 5 10 Gráfico 2.1
30 15 · Simétrica a 3 = 0 0 1 2 3 4 5 6
Gráfico 2.2
· Asimétrica negativamente a 3 < 0 0 0,5 1 1,5 2 2,5 3 Gráfico 2.3 El cuarto momento ( m ) de cualquier variable aleatoria mide que tan puntiaguda es la distribución de probabilidad de X y recibe el nombre de curtosis . 4 m 4 = æ 4 ö
çç ÷÷( - m ) i m
å
i
i = 0 è ø
' 4 - i æ 4ö
æ 4 ö
æ 4 ö
æ 4 ö
æ 4 ö
= çç ÷÷( - m ) 0 m 4 ' + çç ÷÷( - m ) m 3 ' + çç ÷÷( - m ) 2 m 2 ' + çç ÷÷( - m ) 3 m1 ' + çç ÷÷( - m ) 4 m 0 ' è 0 ø
è 1 ø
è 2 ø
è 3 ø
è 4 ø
= m 4 ' - 4mm 3 ' + 6 m 2 m 2 ' - 4 m 3 m 1 ' + m 4 = m 4 ' - 4mm 3 ' + 6 m 2 m 2 ' - 4 m 4 + m 4 = m 4 ' - 4mm 3 ' + 6 m 2 m 2 ' - 3 m 4 31
Al igual que en el tercer momento es recomendable usar el cuarto momento estandarizado, dado por: 2 a 4 = m 4 / m 2 = m 4 / var( X ) 2 · Si a 4 > 3 la distribución de probabilidad presenta un pico relativamente alto y se dice que la variable tiene distribución que recibe el nombre de leptocúrtica 0 5 10 15 20 Gráfico 2.4
· Si a 4 = 3 la distribución no presenta un pico ni muy alto ni muy bajo y recibe el nombre de mesocúrtica. 5 7 9 11 Gráfico 2.5
32 13 15 · Si a 4 < 3 la distribución de probabilidad es relativamente plana y recibe el nombre de platicúrtica. 5 7 9 11 13 15 Gráfico 2.6 Ejemplo 2.1: Encontrar la media, la varianza, y los factores de forma de la distribución exponencial. f ( x ; q ) =
ì 1 - qx ï e íq ï0 î
x > 0, en cualquier otro valor Solución: Primero se debe encontrar los primeros 4 momentos alrededor de cero, para esto:
x ¥
m r ' = E ( x r ) =
x ¥ r x r - q
r - 1 x =
e dx q
ò0 q
ò0 q r e q dx si reemplazamos
u=
x q du =
Þ 1
dx q entonces se tendría que
¥
' m r = q
r
r - u ò u e du = q r G (r + 1 ) = r ! q r 0
Luego
m 1' = E ( X ) = 1 ! q = q
33
m 2' = 2! q 2 = 2q 2 m 3' = 3! q 3 = 6q 3 m 4' = 4! q 4 = 24q 4 ahora ya teniendo los cuatro primeros momentos alrededor de cero, se puede calcular los momentos alrededor de la media. m2
= var( X ) = m 2' - m 2 = 2q 2 - q 2 = q 2
m 3 = m 3 ' - 3mm 2 ' + 2 m 3 = 6q 3 - 3 q ( 2 q 2 ) + 2 q 3 = 6q 3 - 6 q 3 + 2 q 3 = 2q 3 m 4 = m 4 ' - 4 mm 3 ' + 6 m 2 m 2 ' - 3 m 4 = 24q 4 - 4 q ( 6 q 3 ) + 6 q 2 ( 2 q 2 ) - 3 q 4 = 24q 4 - 24 q 4 + 12 q 4 - 3 q 4 = 9q 4 ahora teniendo estos momentos se puede encontrar los coeficientes de asimetría y de curtosis. a 3 = m 3 /( m 2 ) 3 / 2 = m 3 / var( X ) 3 / 2 = 2q 3 /( q 2 ) 3 / 2 = 2. 2 a 4 = m 4 / m 2 = 9q 4 / q 4 = 9. Luego E ( X ) = q , var( X ) = q 2 ,
a 3 = 2,
a 4 = 9. entonces si se observa los factores de forma se tiene que la grafica de una distribución exponencial siempre es asimétrica positivamente y leptocúrtica.
34
DISTRIBUCION EXPONENCIAL 0 5 10 15 20 Gráfico 2.7 Ejemplo 2.2: Encontrar la media, la varianza, y los factores de forma de la distribución de poisson.
f ( X ; l ) = ì e - l lx
ï
í x ! ï0 î
x = 0, 1 , 2 , ... en cualquier otro valor Solución: Para este caso es muy complicado encontrar m r' por esto se procede a encontrarlos uno por uno.
m 1' = E ( X ) = l (ver ejemplo 1.8)
m 2' = E ( X 2 ) = E[ X ( X - 1 ) + X ] = E[ X ( X - 1 )] + E ( X ) ahora ¥
E[ X ( X - 1 )] =
¥
e - l l x l x - 2 = l 2 e -l å
x ! i = 2 ( x - 2 )! x( x - 1 ) å
i =0 ahora si se hace y = x - 2 , se tendría
0 £ y £ ¥ , y por tanto y ¥
E[ X ( X - 1 )] = l 2 e - l l = l 2 e - l e l = l2 ósea que
å
i = 0 ( y )! 35 m 2' = l2 + l
m 3' = E ( X 3 ) = E[ X ( X - 1 )( X - 2 ) + 3 X 2 - 2 X ] = E[ X ( X - 1 )( X - 2 )] + E ( 3 X 2 - 2 X ) ahora e - l l x x
(
x - 1 )( x 2 ) å
x ! i =0 ¥
E[ X ( X - 1 )( X - 2 )] =
l x -3 i = 3 ( x - 3 )! ¥
= l3 e -l å
si se hace y = x - 3 , se tendría 0 £ y £ ¥ , y por tanto l y = l 3 e - l e l = l3 ósea que
(
y )! i = 0 ¥
E[ X ( X - 1 )( X - 2 )] = l3 e - l å
m 3' = l3 + E ( 3 X 2 - 2 X ) = l3 + 3 E ( X 2 ) - 2 E ( X ) = l3 + 3l2 + l
m 4' = E ( X 4 ) = E[ X ( X - 1 )( X - 2 )( x - 3 ) + 6 X 3 - 11 X 2 + 6 X ] = E[ X ( X - 1 )( X - 2 )( x - 3 )] + E ( 6 X 3 - 11 X 2 + 6 X ) ahora e -l lx x ! ¥
E[ X ( X - 1 )( X - 2 )( x - 3 )] =
x( x - 1 )( x - 2 )( x - 3 ) å
i =0 l x - 4 i = 4 ( x - 4 )! ¥
= l 4 e -l å
si se hace y = x - 4 , se tendría 0 £ y £ ¥ , y por tanto l y = l 4 e - l e l = l4
(
y )! i = 0 ¥
E[ X ( X - 1 )( X - 2 )( x - 3 )] = l 4 e - l å
ósea que
m 4' = l4 + E ( 6 X 3 - 11 X 2 + 6 X ) = l4 + 6 E ( X 3 ) - 11 E ( X 2 ) + 6 E ( X ) 36
4
3
2 2 = l + 6 ( l + 3 l + l ) - 11 ( l + l ) + 6 l
= l4 + 6 l3 + 18 l2 + 6 l - 11 l2 - 11 l + 6 l
= l4 + 6 l3 + 7 l2 + l
ahora se procede a calcular los momentos alrededor de la media. m2
= var( X ) = m 2' - m 2 = l2 + l - l2 = l m 3 = m 3 ' - 3mm 2 ' + 2 m 3 = l3 + 3l2 + l - 3 l ( l2 + l ) + 2 l3 = l3 + 3l2 + l - 3 l3 - 3 l2 + 2 l3 = l m 4 = m 4 ' - 4 mm 3 ' + 6 m 2 m 2 ' - 3 m 4 = l 4 + 6l3 + 7 l2 + l - 4 l ( l3 + 3 l2 + l ) + 6 l2 ( l2 + l ) - 3 l4 = l4 + 6l3 + 7 l2 + l - 4 l4 - 12 l3 - 4 l2 + 6 l4 + 6 l3 - 3 l4 2 = 3 l + l
Y con esto calcular los factores de forma a 3 = m 3 /( m 2 ) 3 / 2 = m 3 / var( X ) 3 / 2 = l /(l ) 3 / 2 = l / l3 = 1 / l a 4 = m 4 / m 2 2 = m 4 / var( X ) 2 = 3l2 + l
l
2 = 3+
1 l luego E ( X ) = l , var( X ) = l 2 + l ,
a 3 = 1 / l ,
a 4 = 3 +
1 l Si se observan los factores de forma encontramos que la grafica es asimétrica positiva y leptocúrtica pero a medida de que
l ® ¥ la grafica tiende a ser simétrica y mesocúrtica
37 DISTRIBUCION DE POISSON 0,25 0,2 0,15 0,1 0,05 0 0 2 4 6 8 10 12 Gráfico 2.8 2.2 Funciones gener ador as de momentos Cuando existen todos los momentos de una distribución (esto es cuando todos los momentos son finitos), es posible asociar una función generadora de momentos. Se define esta como E ( e x .t ) donde x es la variable aleatoria y t una variable continua; el valor esperado de e x . t será una función de t que representaremos por
ìåe x. t p ( x ) ïï x x .t M x ( t ) = E ( e ) = í ¥
ï ò e x . t f ( x ) dx ïî- ¥
donde X es discreta donde X es continua M x (t ) Genera todos los momentos de X alrededor del origen. Para demostrar esto se deriva M x (t ) con respecto a t y se evalúa la derivada en t =0 pero antes veamos que: E[ h ( t )]' = E [ h ' ( t )] 38 d d E [ h ( t )] =
å [ h ( t ) P ( x )] dt dt x d = ( t ) P ( x )] åx dt [h =
åx [ h' ( t ) P ( x )] = la derivada de una suma es la suma de las derivadas. E [ h ' ( t )] para el caso continuo hay que tener en cuenta que la derivada de una integral es la integral de la derivada, Ahora si se tiene d r d r =
M ( t ) E ( e x . t ) x r r dt dt t = o t = o é d r = E ê
r ë dt ù
e x . t ú
û
t = o = E ( x r e x . t ) t = o = E ( x r ) = m r' Así como los momentos alrededor de 0 tienen su función generadora de momentos los momentos alrededor de la media también tiene dicha función y se define como:
ìåe t ( x - m ) p ( x ) ïï x M ( x - m ) ( t ) = E ( e t ( x - m ) ) = í ¥
ï ò e t ( x -m ) f ( x ) dx ïî-¥
donde x es discreta donde x es continua M ( x- m ) ( t ) genera todos los momentos alrededor de la media
39 Veamos : d r d r =
M ( t ) E ( e t ( x - m ) ) ( m - x ) r dt r dt t = o t = o é d r = E ê
r ë dt ù
e t ( x - m ) ú
t =o û
= E[( x - m ) r e t ( x -m ) ) t = o = E ( x - m ) r = m r
Ejemplo 2.3: Determinar la función generadora de momentos de:
·
la distribución Gamma
·
la distribución Chi­cuadrado
·
la distribución Exponencial y usela para calcular la media, la varianza y los factores de forma de cada una de las distribuciones. Solución: La distribución Gamma esta dada por f ( x ; a , q ) =
x ì 1 a - 1 q
x e ï
a
íG( a ) q
ï0 î
x > 0, a , q > 0 en cualquier otro valor Luego su función generadora de momentos es: - x ¥
M x (t ) = E ( e x .t ) =
=
1 1 e x. t x a -1 e q dx =
a ò
G ( a ) q 0 G ( a ) q a
1 G ( a ) q a
¥
x q
- (1 -q . t )
a -1 ò x e dx 0 Ahora
40 ¥
x ö
æ
ç x. t - ÷
qø
a -1 ò x e è
0 dx si
u = (1- q . t )
x =
x q
(1- q . t ) dx du =
Þ
Þ dx =
q
q .du 1 - q . t q .u (1 - q . t ) Reemplazando se tiene que 1 M x (t ) =
G ( a ) q a
=
=
a -1 ¥
æ q . u ö
ò0 ççè (1 - q . t ) ÷÷ø
q
du 1 - q . t e -u
¥
q a -1 q
u a -1 e -u du a -1 ò
a
G (a
) q (1 - q . t ) ( 1 - q . t ) 0 qa
a
G (a ) q (1 - q . t ) a
1
G( a ) =
-a
= (1 - q . t )
a
(1 - q t. )
y teniendo esta función se puede calcular los primeros cuatro momentos alrededor de 0. m 1' = d
d
m x (t ) =
(1 - q . t )-a
dt dt t = o [
] -a -1 = - a (1 - q . t ) t = 0 ( -q ) t = 0 -a -1 = qa (1 - q . t ) = qa = m m 2' = d2
d
m ( t ) =
qa (1 - q . t )-a -1 2 x dt dt t = o [
] -a - 2 = q 2 a (a + 1 ) (1 - q . t ) m 3' = t = 0 -a - 2 = qa ( -a
- 1 ) (1 - q . t ) ( -q ) t = 0 t = 0 = q 2a ( a + 1 ) d3
d 2 q a (a + 1 ) (1 - q . t )-a - 2 m ( t ) =
3 x dt dt t = o [
] -a - 3 = q 2 a (a + 1 )( -a - 2 ) (1 - q . t ) ( -q ) t = 0 -a - 3 t = 0 = q 3 a (a + 1 )( a + 2 ) (1 - q . t ) = q 3a ( a + 1 )( a + 2 ) 41 t = 0 t =0 m 4' = d4
d 3 m ( t ) =
q a (a + 1 )( a + 2 ) (1 - q . t )-a -3 4 x dt dt t = o [
] = t = 0 -a - 4 = q 3 a (a + 1 )( a + 2 )( -a - 3 ) (1 - q . t ) ( -q ) t = 0 -a - 4 = q 4 a (a + 1 )( a + 2 )( a + 3 ) (1 - q . t ) t = 0 = q 4a ( a + 1 )( a + 2 )( a + 3 ) ahora se procede a calcular los momentos alrededor de la media m2
= var( X ) = m 2' - m 2 = q 2 a (a + 1 ) - a 2 q 2 = q 2a 2 + q 2 a - a 2 q 2 = q 2 a
m 3 = m 3 ' - 3mm 2 ' + 2 m 3 = q 3 a (a + 1 )( a + 2 ) - 3 ( qa )( q 2 a ( a + 1 )) + 2 q 3 a 3 = q 3 a (a 2 + 3 a + 2 ) - 3 q 3 a 2 ( a + 1 ) + 2 q 3 a 3 = q 3 a 3 + 3a 2 q 3 + 2 q 3 a - 3 q 3 a 3 - 3 q 3 a 2 + 2 q 3 a 3 = 2q 3 a
m 4 = m 4 ' - 4 mm 3 ' + 6 m 2 m 2 ' - 3 m 4 = q 4 a (a + 1 )( a + 2 )( a + 3 ) - 4 qa [ q 3 a ( a + 1 )( a + 2 )] + 6 q 2 a 2 q 2 a ( a + 1 ) - 3 q 4 a 4 = q 4 a (a 3 + 6 a 2 + 11 a + 6 ) - 4 q 4 a 2 ( a 2 + 3 a + 2 ) + 6 q 4 a 4 + 6 q 4 a 3 - 3 q 4 a 4 = q 4a [ a 3 + 6 a 2 + 11 a + 6 - 4 a ( a 2 + 3 a + 2 ) + 6 a 3 + 6 a 2 - 3 a 3 ] = q 4a [ 4 a 3 + 12 a 2 + 11 a + 6 - 4 a 3 - 12 a 2 - 8 a ] = q 4a [ 3 a + 6 ] y por ultimo los factores de forma a 3 = m 3 /( m 2 ) 3 / 2 = m 3 / var( X ) 3 / 2 = 2 a 4 = m 4 / m 2 = m 4 / var( X ) 2 = 2q 3 a
2 3 ( q a ) = 2q 3 a
q
3 a
3 = 2a
a
3 =
2 a 2 ö
q 4 a (3 a + 6 ) (3 a + 6 ) æ
=
= 3 ç1 + ÷
2 2 ( q a ) a
è a ø
luego
42 M X (t ) = (1 - 2 . t ) - v / 2 var( X ) = q 2 a ,
m = qa , 2 a 3 = a æ
è
a 4 = 3 ç1 +
,
2 ö
÷
a ø
si se observan los coeficientes de forma, vemos que la distribución Gamma es asimétrica positivamente y leptocúrtica, si a tiende a 0. Pero tiende a ser mesocúrtica y simétrica a medida de que a tiende a infinito. DISTRIB UCION GAMMA 0 5 10 15 20 Gráfico 2.9 Ahora como la distribución Chi­cuadrado es una distribución Gamma con a =
v
y 2 q = 2 donde v son los grados de libertad de la variable. Entonces:
M X (t ) = (1 - 2 . t ) - v / 2 m = v , var( X ) = 2 v ,
a 3 = 4 2 v ,
æ
4 ö
a 4 = 3 ç1 + ÷
è v ø
Igualmente la distribución exponencial es una distribución Gamma con a = 1 , luego
M X (t ) = (1 - q . t ) -1 43
m = q , var( X ) = q 2 ,
a 3 = 2,
a 4 = 9 Como esta desarrollado en el ejemplo 2.1 NOTA: En el apéndice al final de este documento se enuncian la media, la varianza, los factores de forma y la función generadora de momentos de cada una de las distribuciones especiales.
44
CAPITULO TRES DISTRIBUCIÓN DE PROBABILIDAD DE UNA FUNCIÓN DE UNA VARIABLE ALEATORIA Frecuentemente en estadística se presenta la necesidad de deducir la probabilidad de una función de una o más variables aleatorias. Por ejemplo supongamos que dadas las variables aleatorias X 1 , X 2 ,..., X n y dadas las funciones g 1 ( x 1 , x 2 ,..., x n ); g 2 ( x 1 , x 2 ,..., x n ) ;…; g k ( x 1 , x 2 ,..., x n ) . Queremos en general encontrar la distribución de Y1 , Y 2 ,..., Y n donde Yi = g i ( x 1 , x 1 ,..., x n ) i = 1, 2 , 3 ,..., k Para esto se presentan 3 técnicas:
·
Técnica de la distribución acumulativa
·
Técnica de las transformaciones
·
Técnica de la función generadoras de momentos En este capítulo solo se presentaran las 2 primeras técnicas, la tercera la trataremos mas a fondo en el capítulo 4.
45 3.1 Técnica de la distr ibución acumulativa Esta técnica esta basada como su nombre lo indica en la distribución acumulativa de probabilidades de una variable aleatoria y es útil en distribuciones continuas de una o más variables. Teorema 3.1: Sea donde X una variable aleatoria continua con función de densidad f X ( x ) f X ( x ) > 0 para a ≤ x ≤ b, supóngase la función Y = g ( X ) estrictamente monótona creciente, y derivable, por lo tanto continúa para todo x , entonces la variable aleatoria Y = g ( X ) tiene función de densidad dada por:
f Y ( y ) = f X (g -1 ( y ) )
d -1 (g ( y ) ) dy Demostración:
F Y ( y ) = p ( Y £ y ) = p ( g ( X ) £ y ) = p ( X £ g -1 ( y )) = F X (g -1 ( y ) ) ahora como
f Y ( y ) = F Y ' ( y ) f Y ( y ) = F X ' (g -1 ( y ) )
Ejemplo 3.1: Si 4 propiedad de la distribución acumulativa
d -1 d -1 (g ( y ) ) (
g ( y ) ) = f X (g -1 ( y ) )
dy dy X se distribuye uniformemente en el intervalo (-p / 2 , -p / 2 ) encontrar la distribución de Y = tan( X ) Solución: X » f X ( x ) = U ( -p / 2 , p / 2 ) ß Y = g ( X ) = tan( X ) »
f X ( x ) esta definida como
f Y ( y ) = ? f X ( x ) = 1 p y el intervalo en el que se mueve Y es
- p / 2 £ x £ p / 2 - ¥ £ y = tan( x ) £ ¥ , por tanto
46 F Y ( y ) = p ( Y £ y ) = p (tan( X ) £ y ) = p ( X £ arctan y ) = F X (arctan y ) ß
f Y ( y ) = f X (arctan y )
=
1 1 p 1 + y 2 d (arctan y ) dy - ¥ £ y £ ¥
- ¥ £ y £ ¥
Lo cual indica que la distribución de Y es una distribución de Cauchy con parámetros a = 0 y b = 1 . ¿Que sucedería si g ( X ) fuese una función decreciente? Teorema 3.2: Sea X una variable aleatoria continua con función de densidad donde f X ( x ) f X ( x ) > 0 para a ≤ x ≤ b , suponga la función Y = g ( X ) estrictamente monótona decreciente, y derivable, por lo tanto continúa para todo x , entonces la variable aleatoria y = g ( x ) tiene función de densidad dada por:
f Y ( y ) = - f X (g -1 ( y ) )
d -1 (g ( y ) ) dy Demostración:
F Y ( y ) = p ( Y £ y ) = p ( g ( X ) £ y ) = p ( X ³ g -1 ( y )) = 1 - p ( X £ g -1 ( y )) = 1 - F X (g -1 ( y ) ) ahora como
f Y ( y ) = F Y ' ( y ) f Y ( y ) = - F X ' (g -1 ( y ) )
Ejemplo 3.2: Si d -1 d -1 g ( y ) ) = - f X (g -1 ( y ) )
(
(g ( y ) ) dy dy X se distribuye uniformemente en el intervalo (0,1) encontrar la distribución de Y = -2 ln( X ) 47
Solución: X f X ( x ) = U ( 0 , 1 ) »
ß Y = g ( X ) = -2 ln( X ) »
f Y ( y ) = ? f X ( x ) está definida como f X ( x ) = 1 y el intervalo en el que se mueve 0 £ x £ 1 y es 0 £ y = -2 Ln ( x ) £ ¥ , por tanto
FY ( y ) = p ( Y £ y ) = p ( -2 ln( X ) £ y ) = p ( X ³ e - y / 2 ) = 1 - p ( X £ e - y / 2 ) = 1 - F X (e - y / 2 ) d - y / 2 æ 1 ö
(
e ) = - ç - e - y / 2 ÷
dy è 2 ø
f Y ( y ) = - f X (e - y / 2 )
=
1 - y / 2 e
2 0 £ y £ ¥
Luego la distribución de y es la distribución de una variable Chi­cuadrado con 2 grados de libertad. El problema de esta técnica es que solo sirve para distribuciones continuas ya que en las distribuciones discretas no se cumplo que
f Y ( y ) = F Y ' ( y ) . El ejemplo que sigue es muy particular porque recordemos que las funciones acumulativas tienen la propiedad de:
y F Y ( y ) = p (Y £ y ) = p ( g ( X ) £ y ) =
ò f ( x ) dx - ¥
y mas general quedaría
y y y F Y ( y ) = p (Y £ y ) = p ( g ( X 1 , X 2 , X 3 , ) £ y ) =
ò ò ò f ( x , x , x ) dx dx dx 1 2 3 1 2 3 - ¥-¥- ¥
Ejemplo 3.3: Sea X 1 , X 2 , X 3 variables aleatorias independientes cada una con distribución normal estándar. Halle la distribución de Y Solución:
48 X1 »
f X ( x 1 ) =
X 2 »
f X ( x 2 ) =
X 3 »
f X 3 ( x 3 ) =
1 2 1 2 p
1 2 p
1 - x 1 2 2 e - ¥ £ x1 £ ¥
1 - x 2 2 e 2 - ¥ £ x 2 £ ¥
1 1 - 2 x 3 2 e 2 p
- ¥ £ x 3 £ ¥
Luego la función conjunta es:
- ¥ £ x1 £ ¥
1 2 - ( x 1 2 + x 2 + x 3 2 ) 1 2 f X 1 , X 2 , X 3 ( x 1 , x 2 , x 3 ) = e
( 2 p ) 3 / 2 - ¥ £ x 2 £ ¥
- ¥ £ x 3 £ ¥
F Y ( y ) = p ( Y £ y ) = p ( x 12 + x 2 2 + x 3 2 £ y ) .
F Y ( y ) =
1 - ( x 1 2 + x 2 2 + x 3 2 ) 1 e 2 3 / 2 òòò
p ) A (2 dx 1 dx 2 dx 3 donde A es la región determinada por el circulo de centro ( 0 , 0 , 0 ) y de radio se hace un cambio de variables. Entonces si:
x1 = r cos q . sen j ,
x 2 = r sen q . sen j ,
x 3 = r cos j
y , 0 £ q £ 2 p , 0 £ j £ p
donde 0 £ r £
Luego X 12 + X 22 + X 32 = r 2 cos 2 q . sen 2 j + r 2 sen 2 q .sen 2 j + r 2 cos 2 j
=
r 2 [cos 2 q . sen 2 j + sen 2 q .sen 2 j + cos 2 j ] =
r 2 [.sen 2 j (cos 2 q + sen 2q ) + cos 2 j ] =
r 2 [.sen 2 j + cos 2 j ] = r
2
49 y , para facilidad Luego F Y ( y ) = ò
y 2 p
0 0 0 2
y 2 p
1 - r 2 e 2 r 2 d q d r
3 / 2 ò (2 p )
0 =ò
1 - r 2 e 2 r 2 sen j d j d q d r
3 / 2 ò ò (2 p )
0 =ò
1
p
0 y 1 2( 2 p ) - 2 r 2 2 e r d r = 2 p 2 p
Þ dr
=
2
ò
p
y
0 1 - r 2 r 2 e 2 d r = 2 p
w Þ r 2 = w
si hacemos r =
F Y ( y ) = 2
y w p ò0 2 -
1
dw 2 w w
e 2 dw = 2
p
ò
y w 2 0 -
w
e 2 dw ß f Y ( y ) =
y 2 y - 2 e p 2 y =
1 ( y) 3 / 2 -1 e 2 2 p ahora veamos que:
G (3 / 2 )2 3 / 2 = 2 p 1
G(3 / 2 ) 2 3 / 2 = G(1 / 2 ) 2 2 = p 2 = 2p 2 Luego y 1 1 æ 1 ö
3 / 2 -1 2 f Y ( y ) =
( y
) e = ç ÷
3 / 2 G(3 / 2 ) 2 G(3 / 2 ) è 2 ø
o sea que 3 / 2 3 / 2 -1 ( y) -
e y 2 Y tiene una distribución Chi­cuadrado con 3 grados de libertad.
50 ò
0 y
1 - r 2 rr e 2 d r
3.2 Técnica de transfor maciones Esta técnica es usada tanto en distribuciones discretas como en distribuciones continuas. 3.2.1 Técnica de tr ansformaciones par a var iables discr etas Teorema 3.3: Supóngase que X es una variable aleatoria discreta con distribución de probabilidad f X ( x ) . Si la función Y =
los valores g ( X ) define una transformación uno a uno entre X y Y , de tal forma que la ecuación y = g ( x ) tenga su inversa x = g ( y ) , entonces la distribución de Y es:
f X (g -1 ( y ) ) f Y ( y ) =
Demostración:
F Y ( y ) = p ( Y = y ) = p ( g ( X ) = y ) = p ( X = g -1 ( y )) = f X (g -1 ( y ) ) Ejemplo 3.4: Sea X es una variable aleatoria discreta donde su distribución se encuentra dada por ì x ï
f X ( x ) = P ( X = x ) = í10 ïî0 Encontrar la distribución de x = 1, 2 , 3 , 4 en cualquier otro caso Y = 3 X + 1 Solución: si X varia entre 1 y 4 se ve claramente que Y 4,7,10,13, entonces y = g ( x ) = 3 x + 1 Þ x = g -1 ( y ) =
y - 1 3 ahora
æ
è
f Y ( y ) = p ( Y = y ) = p ( 3 X + 1 = y ) = p ç X =
51 y - 1 ö
æ y - 1 ö
÷ = f X ç
÷
3 ø
è 3 ø
æ y - 1 ö
÷
è 30 ø
f Y ( y ) = ç
y se encuentra dada por: Luego la distribución de y = 4, 7 , 10 , 13 ì y - 1 ï
f Y ( y ) = P (Y = y ) = í 30 ïî0 en cualquier otro caso Supongamos ahora el problema en el que X 1 , X 2 ,..., X n , son variables aleatorias discretas con función conjunta f X 1 , X 2 ,..., X n ( x 1 , x 2 ,..., x n ), y se desea encontrar la probabilidad conjunta f Y , Y ,..., Y n ( y 1 , y 2 ,..., y n ) de las nuevas variables aleatorias 1
2 y1 = g 1 ( x 1 , x 2 ,..., x n ), y 2 = g 2 ( x 1 , x 2 ,..., x n ), ..., y n = g n ( x 1 , x 2 ,..., x n ), las cuales definen una transformación uno a uno entre los conjuntos de puntos ( x 1 , x 2 ,..., x n ) y ( y 1 , y 2 ,..., y n ) .Si se resuelven las ecuaciones simultáneamente se encontrara la solución inversa única x1 = g 1 -1 ( y 1 , y 2 ,..., y n ), x 2 = g 2 -1 ( y 1 , y 2 ,..., y n ), ..., x n = g n -1 ( y 1 , y 2 ,..., y n ), Teorema 3.4: Supóngase que X 1 , X 2 ,..., X n , son variables aleatorias discretas con distribución de probabilidad conjunta f X , X ,..., X n ( x 1 , x 2 ,..., x n ) . Si las funciones 1
2 y1 = g 1 ( x 1 , x 2 ,..., x n ), y 2 = g 2 ( x 1 , x 2 ,..., x n ), ..., y n = g n ( x 1 , x 2 ,..., x n ), definen una transformación uno a uno entre los valores ( x 1 ,..., x n ) y ( y 1 ,..., y n ) de tal forma que las ecuaciones y1 = g 1 ( x 1 ,..., x n ),..., y n = g n ( x 1 ,..., x n ) tengan inversa respectivamente x1 = g 1 -1 ( y 1 ,..., y n ),..., x n = g n -1 ( y 1 ,..., y n ), entonces de Y 1 , Y 2 ,..., Y n , es:
f Y ,..., Y n , ( y 1 ,..., y n ) = f X ,..., X n [ g 1 -1 ( x 1 ,..., x n ),... g n -1 ( x 1 ,..., x n )] 1
1
52
la distribución conjunta Demostración: f Y , Y ,..., Y n , ( y 1 , y 2 ,..., y n ) 1
2 = p ( Y 1 = y 1 , Y 2 = y 2 , ... , Y n = y n ) = p ( g 1 ( x 1 , x 2 ,... x n ) = y 1 , g 2 ( x 1 , x 2 ,... x n ) = y 2 , ... , g n ( x 1 , x 2 ,... x n ) = y n ) = p ( x 1 = g 1- 1 ( y 1 , y 2 ,... y n ), x 2 = g -2 1 ( y 1 , y 2 ,... y n ), ..., x n = g n -1 ( y 1 , y 2 ,... y n )) f X , X ,..., X n [ g 1 -1 ( x 1 , x 2 ,..., x n ), g 2 -1 ( x 1 , x 2 ,..., x n ),... g n -1 ( x 1 , x 2 ,..., x n )] =
1
2 Ejemplo 3.5: Sean X 1 y X 2 variables aleatorias independientes de poisson. Halle la distribución de la suma de dichas variables. Solución: l1 x e - l
x 1 ! 1 X 1 » f X ( x 1 ) =
1
1 x 1 = 0,1,2,3,… l1 x e - l
x 2 ! 2 X 2 » f X ( x 2 ) =
2
1
2 x 2 = 0,1,2,3,…
l1 x l 2 x e - ( l +l ) x 1 ! x 2 ! 1
f X , X ( x 1 , x 2 ) = 2 2 1 2 x 1 , x 2 = 0,1,2,3,… Y1 = X 1 + X 2 Þ f Y ( y 1 ) = ? 1
Usamos una variable auxiliar para poder tener una transformación uno a uno. y2 = x 2 Ahora si procedemos a encontrar las inversas: x1 = y 1 - x 2 Þ x1 = y 1 - y 2 = g1- 1 ( y 1 , y 2 ) x2 = y 2 Y los Intervalos de = g 2- 1 ( y 1 , y 2 ) y 1 y y 2 son: x1 ³ 0 Þ y1 - y 2 ³ 0 Þ y2 £ y 1 x2 ³ 0 Þ y2 ³ 0 Þ 0 £ y2 £ y 1 0 £ y 1 £ ¥
por tanto y 1 = 0,1,2,3,…
53 y 2 = 0,1,2,3,…, y 1 aplicando el teorema encontramos la distribución conjunta de Y 1 y Y 2 es f Y , Y ( y 1 , y 2 ) =
1
f X , X ( y 1 - y 2 , y 2 ) 2 1
2 l1 y y l2 y e -( l +l ) ( y 1 - y 2 )! y 2 ! 1- 2 = 2 1 2 y para encontrar la distribución de f Y 1 ( y 1 ) , se calcula la distribución marginal de Y1, sumando la distribución conjunta con respecto a l1 y - y l 2 y e - ( l +l ) å0 ( y - y )! ( y )! 1 2 2 y 1 f Y ( y 1 ) =
1
y 1 å f Y , Y ( y 1 , y 2 ) =
1 2 0 1 1
2 2 1 2 l1 y - y l2 y å0 ( y - y )! ( y )! 1 2 2 y 1 1 2 2 e - ( l +l
= e - ( l + l ) y y 1 ! l1 y - y l2 y å
y 1 ! 0 ( y 1 - y 2 )! ( y 2 )! = e - ( l +l ) ( l1 + l2 ) y y 1 ! 1 2 ) 2 1 1 1 1
2 =
1 f Y ( y 1 ) = e - ( l +l ) y 2 , entonces: ( l1 + l2 ) y1 y 1 ! 2 2 2 1 y 1 = 0,1,2,3,… Luego la distribución de la suma de 2 variables de poisson es una variable de poisson con parámetro l1 + l2 .
54 3.2.1 Técnica de transformaciones para variables continuas En este caso se enuncia el siguiente teorema: Teorema 3.5: Supóngase que X es una variable aleatoria continua con distribución de probabilidad f X ( x ) . Si la función entre los valores y = g ( x ) define una correspondencia uno a uno X y Y ,de tal forma que la ecuación y = g ( x ) tenga su inversa x = g -1 ( y ) , entonces la distribución de Y es:
f Y ( y ) = f X (g -1 ( y ) ) J donde J =
d -1 g ( y ) y recibe el nombre de jacobiano de la transformación. dy Demostración: La demostración puede abrirse en dos casos, en el caso en el que creciente y en el caso en el que ·
Supongamos que y = g ( x ) es decreciente.
y = g ( x ) es creciente. 4 b a 0 0 g­1(a) escojamos dos puntos arbitrarios de 1,5 y , por ejemplo a y b entonces:
55 y = g ( x ) es P (a £ Y £ b ) = P (Y £ b ) - P ( Y £ a ) = P ( g ( X ) £ b ) - P ( g ( X ) £ a ) = P ( X £
g -1 ( b )) - P ( X £ g -1 ( a )) -1 = P[ g ( a ) £
X £ g -1 ( b )] g -1 ( b ) =
ò f X g - 1 ( a ) ( x ) dx Ahora cambiando la variable de integración de x a y por la relación x = g -1 ( y ) se tendría que: dx = [ g -1 ( y )] ' dy luego b P (a £ Y £ b ) =
-1 òa f X ( g ( y ))[ g -1 ( y )] ' dy como a y b recorren todos los valores permisibles de y siempre que a < b se tiene que f Y ( y ) = f X ( g -1 ( y ))[ g -1 ( y )] ' (
) = f X g -1 ( y ) . J Se conoce a J = [ g -1 ( y )] ' como el reciproco de la pendiente de la línea tangente a la curva de la función creciente y = g ( x ) es obvio entonces que J = J . Luego
f Y ( y ) = f X (g -1 ( y ) ) J
·
Supongamos que y = g ( x ) es decreciente.
56 b a 0 g­1(a) 0 5 escojamos otra vez puntos arbitrarios de y , a y b entonces: P (a £ Y £ b ) = P (Y £ b ) - P ( Y £ a ) = P ( g ( X ) £ b ) - P ( g ( X ) £ a ) = P ( X £
g -1 ( b )) - P ( X £ g -1 ( a )) -1 = P[ g ( b ) £
X £ g -1 ( a )] g -1 ( a ) =
ò f X ( x ) dx g - 1 ( b ) otra vez cambiando la variable de integración de x a y se tiene que: a P (a £ Y £ b ) =
-1 òb f X ( g ( y ))[ g -1 ( y )] ' dy b = - f X ( g -1 ( y ))[ g -1 ( y )] ' dy òa como a y b recorren todos los valores permisibles de y siempre que a < b se tiene que P (a £ Y £ b ) = - f X (g -1 ( y ) ). J en este caso la pendiente de la curva es negativa, por tanto J = - J .
57 f Y ( y ) = f X (g -1 ( y ) ) J con lo cual se concluye el teorema. Ejemplo 3.6: Sea X variable aleatoria B(a , b ) . Halle la distribución de y = 1 - x . Solución: X »
f X ( x ) =
G ( a + b ) a -1 x ( 1 - x ) b -1 G( a ) G ( b ) Y = g ( X ) = 1 - X Þ f Y ( y ) = ? encontramos la inversa de g ( X ) x = 1 - y = g -1 ( y ) Y el intervalo en el que se mueve y es: 0 £ y = 1 - x £ 1 aplicando el teorema encontramos la distribución de Y
f Y ( y ) = f X (1 - Y ) - 1
= f X (1 - Y ) =
G(a + b ) ( 1 - Y ) a -1 ( Y ) b -1 G( a ) G( b ) Luego Y es una distribución B( b , a ) 58
0 £ x £ 1 Teorema 3.6: Supóngase que X 1 , X 2 ,..., X n son variables aleatorias continuas con distribución de probabilidad conjunta f X 1 , X 2 ,..., X n , ( x 1 , x 2 ,..., x n ) . Si y1 = g 1 ( x 1 , x 2 ,..., x n ), y2 = g 2 ( x 1 , x 2 ,..., x n ), ..., y n = g n ( x 1 , x 2 ,..., x n ), definen una transformación uno a uno entre los valores ( x 1 , x 2 ,..., x n ) y ( y 1 , y 2 ,..., y n ) de tal forma que las ecuaciones y1 = g 1 ( x 1 , x 2 ,..., x n ), y 2 = g 2 ( x 1 , x 2 ,..., x n ),..., y n = g n ( x 1 , x 2 ,..., x n ), tengan inversa x1 = g 1 -1 ( y 1 , y 2 ,..., y n ), x 2 = g 2 -1 ( y 1 , y 2 ,..., y n ),..., x n = g n -1 ( y 1 , y 2 ,..., y n ), , respectivamente entonces la distribución conjunta de Y 1 , Y 2 ,..., Y n , es: f Y , Y ,..., Y n , ( y 1 , y 2 ,..., y n ) 1
2 = f X 1 , X 2 ,..., X n [ g 1 -1 ( x 1 , x 2 ,..., x n ), g 2 -1 ( x 1 , x 2 ,..., x n ),... g n -1 ( x 1 , x 2 ,..., x n )] J donde el jacobiano es el determinante de n x n. ¶x 1 y 1 y 2 ¶x 2 ¶x 2 J = y 1 y 2 ¶x n ¶x n y 1 y 2 M Ejemplo 3.7: Sean ¶x 1 ... ¶x 1 ... ¶x n M
y n y 2 M
... ¶x n y n X 1 y X 2 variables aleatorias independientes con distribución normalmente estandarizada. Halle la distribución del cociente de dichas variables. Solución: 1 X1 »
N ( 0 , 1 ) = f X ( x 1 ) =
1 - 2 x 1 2 e 2 p
X1 »
N ( 0 , 1 ) = f X ( x 2 ) =
1 - 2 x 2 2 e 2 p
1 - ¥ £ x1 £ ¥
1 2 1 - ¥ £ x2 £ ¥
- ¥ £ x1 £ ¥
1 - 2 ( x 1 2 + x 2 2 ) f X 1 , X 2 ( x 1 , x 2 ) = e
2 p
- ¥ £ x 2 £ ¥
59 y1 =
x 1 x 2 Þ f Y 1 ( y 1 ) = ? Usamos una variable auxiliar para poder tener una transformación uno a uno y2 = x 1 + x 2 procedemos a encontrar las inversas: y2 = x 1 + x 2 Þ y2 = y 1 x 2 + x 2 y2 = ( y 1 + 1 ) x 2 x 2 = x 1 = y 2 = g 2- 1 ( y 1 , y 2 ) ( y 1 + 1 ) y 1 y 2 = g1- 1 ( y 1 , y 2 ) ( y 1 + 1 ) Y los Intervalos de y 1 y y 2 son: en este caso no hay ninguna restricción luego
- ¥ £ y 1 £ ¥
- ¥ £ y2 £ ¥
y el jacobiano es y 2
( y + 1 ) 2 J = 1 y 2 ( y 1 + 1 ) 2 y 1 y 1 + 1 1 y 1 + 1 = y 2 y 2 y 1 y (1 + y 1 ) +
= 2 = y 2 ( y 1 + 1 ) -2 3 3 ( y 1 + 1 ) ( y 1 + 1 ) ( y 1 + 1 ) 3 aplicando el teorema encontramos la distribución conjunta de Y 1 y Y 2 es æ y 1 y 2 y 2 ö
÷÷ y 2 ( y 1 + 1 ) -2 , è y 1 + 1 y 1 + 1 ø
f Y , Y ( y 1 , y 2 ) = f X , X çç
1
2 1 =
1 e
2 p 2 2 2 1 é æ y y ö æ y ö ù
- ê çç 1 2 ÷÷ + çç 2 ÷÷ ú
2 ê è y 1 +1 ø è y 1 +1 ø ú
ë
û
2 2 1 æ y 2 ( y 1 +1 ) ö
÷
( y 1 +1 ) 2 ÷ø
1 - 2 ççè
=
e
2 p y 2 ( y 1 + 1 ) -2 y2 ( y 1 + 1 ) 2 - ¥ £ y 2 £ ¥ , - ¥ £ y1 £ ¥
60 y para encontrar la distribución de f Y 1 ( y 1 ) integramos la distribución conjunta con y 2 , entonces: respecto a ¥
¥
1 æ y22 ( y 1 2 +1 ) ö
÷
( y 1 +1 ) 2 ÷ø
1 - 2 çç
f Y 1 ( y 1 ) = ò f Y1 , Y 2 ( y 1 , y 2 ) dy 2 = ò e è
2 p
-¥
-¥
y 2 ( y 1 + 1 ) 2 dy 2 ahora, si hacemos u = 1 y 2 2 ( y 1 2 + 1 ) 2 ( y 1 + 1 ) 2 du =
Þ ( y 1 2 + 1 ) y 2 dy 2 Þ
( y 1 + 1 ) 2 0 £ u £ ¥
luego f Y ( y 1 ) =
1
=
¥
y 2 ( y 1 + 1 ) 2 1 -u
e du 2 p ò0 ( y 1 + 1 ) 2 ( y 1 2 + 1 ) y 2 2 -u
e 2 p ( y + 1 ) ò
2 1 = 1 p ( y12 + 1 ) f Y ( y 1 ) = 1 p ( 1 + y12 ) 1
¥
du 0 - ¥ £ y 1 £ ¥
con lo que se tiene que la distribución del cociente de 2 variables normal estándar es una variable de Cauchy con a = 0 y b = 1
61 CAPITULO CUATRO TÉCNICA DE FUNCIÓN GENERADORA DE MOMENTOS 4.1 Descr ipción de la técnica Este es otro método para determinar la distribución de variables aleatorias, es construido en base a la función generadora de momentos y es muy útil en algunos casos. “Supongamos las variables aleatorias X 1 ,..., X n con función de densidad conjunta f X ,..., X n ( x 1 ,..., x n ) y las funciones g 1 ( x 1 ,..., x n ) ,…, g k ( x 1 ,..., x n ) , se desea encontrar la 1
distribución de Y1 = g 1 ( x 1 ,..., x n ) ,…, Yk = g k ( x 1 ,..., x n ) apoyados en que si la función generadora de momentos de Y1 , Y 2 ,..., Y k existe es: M Y ,..., Y n ( t 1 ,..., t k ) 1
= E [exp( t 1Y 1 + ... + t k Y k ) ] =
ò ... ò exp( t Y + ... + t k Y k ) f X =
ò ... ò exp [g ( x ,..., x n ) t + ... + g k ( x ,..., x n ) t k ] f X 1 ,..., X n 1 1 1 1 1 ( x 1 ,..., x n ) dx 1 ... dx n 1 ,..., X n 1 62 ( x 1 ,..., x n ) dx 1 ... dx n Después de encontrar la solución de la anterior integral, esta solución estará dada en función de t1 ,..., t k y puede ser reconocida como la función generadora de momentos de alguna distribución conocida, luego Y1 , Y 2 ,..., Y k tendrá dicha distribución gracias a que la función generadora de momentos un única. En el caso de que k > 1 este método puede ser de uso limitado ya que porque podemos reconocer pocas funciones generadoras de momentos. Para k = 1 la función generadora de momentos tendrá un solo argumento por tanto será sencillo reconocer las su función generadora de momentos. Esta técnica es muy útil cuando deseemos encontrar la distribución de la suma de variables independientes” 8 . Ejemplo 4.1: Sea X una variable aleatoria con una distribución Weibull de parámetros
a y q , obtener la distribución de Y = X a Solución:
X »
é æ x ö
a f X ( x ) = a x a -1 exp ê - ç ÷
q
êë è q ø
ù
ú
úû
x > 0; a , q > 0 ¥ ò exp (x t ) f ( x ) dx = M y (t ) = E [exp (x t )] =
a a
a
X
0 a
¥
=
é
a
æ x ö
xa -1 exp ê x a t - ç ÷
a ò
q 0 èq ø
êë
ù
ú dx úû
=
ù
a ¥ a -1 é x a
x exp ê- a (1 - q a t )ú dx a ò
q 0 ë q
û
Si hacemos u =
8 xa
axa - 1
a
(1 - q a t )dx Þ =
(
)
1
- q
t Þ
du qa
qa
x a -1 dx =
Introduction to the theory of statistics. Mood,Graybill, Boes. Pág 96
63 qa
du a (1 - q a t ) Luego reemplazando se tiene que: M y (t ) = a ¥ -u
qa
e du q a ò0 a (1 - q a t ) ¥
= = 1
e -u du ( 1 - q a t ) ò0 1 a
( 1 - q t ) = (1 - q a t ) -1 Luego Y es una distribución exponencial negativa con parámetro
X tiene una distribución normal con media 0 y varianza Ejemplo 4.1: Supóngase que 1, sea Y =
X 2 , encontrar la distribución de probabilidad de Y Solución: - x 2 X
»
f X ( x ) =
1 e 2 2 p
- ¥ £ x £ ¥
¥
ò exp (x t ) f ( x ) dx M y (t ) = E [e Y . t ] =
2 X - ¥
=
1 2 p
¥
ò exp (x t - x / 2 )dx = 2
2 -¥
¥
=
é x 2
ù
exp ê- ( 1 - 2 t ) ú dx = ò
2 p -¥ ë 2 û
=
2 é 1 æ
x ö ù
÷ ú dx exp ê- ç
2 p -ò¥ êë 2 çè 1 /( 1 - 2 t ) ÷ø úû
1 1
q a . ¥
Luego
64 mx
s x2 = 1 /( 1 - 2 t ) Þ s x = 1 / ( 1 - 2 t ) = (1 - 2 t ) -1 / 2 = 0, asi é 1 æ x - m ö 2 ù
x ÷÷ ú dx = (1 - 2 t ) -1 / 2 exp ê- çç
2 s
2 p s x êë
x ø ú
è
û
¥
-1 / 2 M y (t ) = (1 - 2 t ) 1 ò
-¥
Luego Y posee una distribución Chi­cuadrado con 1 grado de libertad. Entonces la distribución del cuadrado de una distribución normal estándar es una distribución Chi­ cuadrado con 1 grado de libertad En el siguiente ejemplo será necesario manipular la expresión con el fin de evitarnos la integración y encontrar la función generadora de momentos. Ejemplo 4.3: Sea X 1 y X 2 variables aleatorias independientes cada una con distribución normal estándar. Halle la distribución de Y =
( X 2 - X 1 ) 2 2 Solución: X1 »
f X ( x 1 ) =
X 2 »
f X ( x 2 ) =
1 2 1 2 p
1 2 p
1 - x 1 2 e 2 - ¥ £ x1 £ ¥
1 - x 2 2 e 2 - ¥ £ x 2 £ ¥
Luego la función conjunta es:
1 f X , X ( x 1 , x 2 ) = 1
2 - ¥ £ x 1 £ ¥
1 - 2 ( x 1 2 + x 2 2 ) e
2 p
- ¥ £ x 2 £ ¥
ahora é æ ( x - x ) 2 t ö ù
M y (t ) = E êexp çç 2 1 ÷÷ ú =
2 øû
ë è
¥ ¥
æ ( x 2 - x 1 ) 2 t ö
exp ò ò ççè 2 ÷÷ø f X 1 , X 2 ( x 1 , x 2 ) dx 1 dx 2 = - ¥- ¥
¥ ¥
=
æ ( x2 - x 1 ) 2 t - ( x 1 2 + x 2 2 ) ö
1 ÷÷dx 1 dx 2 exp ò ò 2 p ççè
2 ø
- ¥- ¥
entonces
65 ( x2 - x 1 ) 2 t - ( x 1 2 + x 2 2 ) 1 = - [( x12 + x 2 2 ) - ( x 2 - x 1 ) 2 t ] 2 2 1 = - [ x12 + x 2 2 - x 2 2 t + 2 x 2 x 1 t - x 1 2 t ] 2 1 = - [ x12 ( 1 - t ) + x 2 2 ( 1 - t ) + 2 x 2 x 1 t ] 2 2 x x t öù
1 é
æ
= - ê x 2 2 ( 1 - t ) + ( 1 - t ) ç x 1 2 + 2 1 ÷ú
2 ë
1 - t øû
è
é 2 2 x 2 x 1 t æ x 2 t ö 2 æ x 2 t ö 2 ù ù
1 é 2 = - ê x 2 ( 1 - t ) + ( 1 - t ) ê x 1 +
+ç
÷ -ç
÷ úú
2 ê
1 - t è 1 - t ø è 1 - t ø ûú ú
ê
ë
ë
û
2 x 2 t ö ( x 2 t ) 2 ù
1 é 2 æ
= - ê x 2 ( 1 - t ) + ( 1 - t ) ç x 1 +
÷ ú
2 ëê
1 - t ø
1 - t ûú
è
x 2 (1 - t ) 1 ( x 2 t ) 2 ( 1 - t ) æ
x t ö
= - 2 +
ç x 1 + 2 ÷
2 2 1 - t 2 è
1 - t ø
2 Luego 2 é x2 ( 1 - t ) x 2 2 t 2 x 2 t ö ù
1 ( 1 - t ) æ
exp - +
x +
ç
÷
ê
ò ò 2 p ê 2 2 ( 1 - t ) 2 è 1 1 - t ø úúdx 1 dx 2 - ¥- ¥
ë
û
¥ ¥
M y (t ) =
1 = 2 p
2 é ( 1 - t ) æ
æ x2 ( 1 - t ) x 2 2 t 2 öìï ¥
x 2 t ö ù üï
ò exp ççè - 2 + 2 ( 1 - t ) ÷÷øíï-ò¥exp êê- 2 çè x 1 + 1 - t ÷ø úú dx 1 ýïdx 2 -¥
ë
û þ
î
¥
ahora x t ö
æ
ç x1 + 2 ÷
2 x 2 t ö
(1 - t ) æ
1 è
1 - t ø
- ç x 1 +
÷ = 2 è
1 - t ø
2 1 /( 1 - t ) 2 Luego si hacemos: m1
x2 t , s x2 = 1 /( 1 - t ) Þ s x = 1 /( 1 - t ) = 1 / ( 1 - t ) 1 - t = - 1
1
66 entones M y (t ) é 1 æ x - m ö 2 ù üï
æ x2 ( 1 - t ) x 2 2 t 2 öìï 1 ¥ 1 ç
÷
ê- çç 1 1 ÷÷ ú dx 1 ýdx 2 exp +
exp í
ò-¥ çè
ò
÷
2 2 ( 1 - t ) øï 1 - t -¥ 2 p s 1 êë 2 è s 1 ø úû ïþ
î
¥
= 1 2 p
= 1 2 p
æ x2 ( 1 - t ) x 2 2 t 2 ö 1 exp ò ççè - 2 + 2 ( 1 - t ) ÷÷ø 1 - t dx 2 -¥
1 æ x 2 ( 1 - t ) x 2 2 t 2 ö
ç÷dx 2 exp +
2 2 ( 1 - t ) ÷ø
1 - t -ò¥ çè
= ¥
2 p
¥
1 luego - x2 ( 1 - t ) 2 +
x 2 2 t 2 =
2 ( 1 - t ) - t 2 ù
( 1 t ) 2 êë
( 1 - t ) úû
=
- x 2 é ( 1 - t ) 2 - t 2 ù
ê
ú
2 ë ( 1 - t ) û
=
- x 2 é1 - 2 t + t 2 - t 2 ù
ê
ú
2 ë
( 1 - t ) û
=
- x 2 é 1 - 2 t ù
2 êë ( 1 - t ) úû
=
ù
x 22 1 é
- ê
ú
2 ë ( 1 - t ) /( 1 - 2 t ) û
x 2 é
Luego si hacemos: m2
2 = 0, s x2 = (1 - t ) /( 1 - 2 t ) Þ s x1 = (1 - t ) /( 1 - 2 t ) de aquí M y (t ) = 1 2 p
1 1 - t
¥
æ 1 ö
x 2 2 ç
exp ò-¥ çè 2 ( 1 - t ) /( 1 - 2 t ) ÷÷ødx 2 67 1 = 1 - 2 t -ò¥
1 - t
1
= ¥
1 - t æ 1 æ x - m ö 2 ö
2 ÷÷ ÷dx 2 exp ç - çç 2 ç
2 è s 2 ø ÷
2 p s 2 è
ø
1 -1 / 2 1 - 2 t = (1 - 2 t ) Lo cual indica que Y también es una distribución Chi­cuadrado con 1 grado de libertad. 4.2 Distr ibución de suma de var iables independientes En esta sección utilizaremos la técnica de la función generadora de momentos para encontrar la distribución de la suma de variables aleatorias independientes. Teor ema 3.1: Si X 1 , X 2 ,…, X n son variables aleatorias independientes y la función generadora de momentos existe para todo - h £ t £ h para algún h > 0 , sea
n
Y = å a i X i entonces. i =1 n M Y (t ) = M x ( a i t ) Õ
i i =1 Demostr ación: é
n ù
ë
1 û
M Y (t ) = E êexp å a i X i t ú = E [exp( a 1 X 1 t + ... + a i X i t ) ] = E [exp( X 1 a 1 t )... exp( X i a i t ) ] n
= E [exp( X 1 a 1 t ) ]... E [exp( X i a i t ) ] = Õ E [exp( X i a i t ) ] = i =1 68 n M x ( a i t ) Õ
i i =1 El poder del anterior teorema es grande puesto que si pudiésemos reconocer
n M x ( t ) esta seria la función generadora de momentos de la variable aleatoria
Õ
i i =1 n
Y = å X i luego sabríamos como se distribuye la suma de las X i . i =1 Ejemplo 4.4: Sea X 1 , X 2 ,…, X n variables aleatorias Gamma independientes, encontrar la distribución de Y = X 1 + X 2 + ... + X n Solución:
X i M X i ( t ) = ( 1 - q . t ) - a
» n M Y (t ) = n M x (t ) Õ
i i =1 = (1 - q . t ) a
Õ
i -
= ( 1 - q . t ) - n a
=1 Lo cual indica que Y tiene una distribución Gamma con parámetros
q y n a . En el ejemplo 3.3 del capitulo tres vimos que la suma de los cuadrados de 3 distribuciones normales estándar poseen una distribución Chi­cuadrado con 3 grados de libertad, con el siguiente ejemplo se demostrara mas general. Ejemplo 4.5: Supóngase que X 1 , X 2 ,…, X n son variables aleatorias independientes que poseen una distribución normal con media 0 y varianza 1, encontrar la distribución de la suma: Solución: Supóngase que Y = X 1 + X 2 + ... + X n En el ejemplo 4.1 se vio que la distribución del cuadrado de una distribución normal estándar es una distribución Chi­cuadrado con 1 grado de libertad luego X i2 » M X i (t ) = ( 1 - 2 . t ) -1 / 2 69 aplicando el teorema n M Y (t ) = n M x (t ) Õ
i i = =1 -1 / 2 ( 1 - 2 . t ) Õ
i = (1 - 2 . t ) - n / 2 =1 Luego la suma de variables Chi­cuadrado posee una distribución Chi­cuadrado con n grados de libertad. Ejemplo 4.6: Mostrar que si X 1 , X 2 ,…, X n son variables aleatorias independientes de poisson cada una con parámetro l i , entonces la distribución de la suma es también una variable aleatoria de poisson con parámetro igual a
å li . Solución: Sea Y = X 1 + X 2 + ... +
X i X n M X (t ) = exp l i (e t - 1 ) » n M Y (t ) = n M x (t ) Õ
i i =1 = exp li (e t - 1 ) = Õ
i n (
)
exp å li e t - 1 i =1 =1 Lo cual muestra la suma tiene una distribución de poisson con parámetro
å li . Ejemplo 4.7: supóngase X 1 , X 2 ,…, X n variables aleatorias independientes con 2 distribución normal de parámetros m i s i2 , luego a i X i » N ( a i m i ; a i 2s
i ) y también n
2 2 M a i X i (t ) = exp( a i m i t + a i 2s
i t / 2 ) . Halle la distribución de Y = å a i x i i =1 Solución: n M Y (t ) = n n 2 2 2 Õ M a x ( t ) = Õ exp(a i m i t + a i s i t i i i =1 i =1 éæ n ö æ n ö t 2 ù
= exp êç å a i m i ÷t + ç å a i 2 s i 2 ÷ ú l
ø è i =1 ø 2 û
ëè i = 1 70 / 2 ) = exp å ( a i m i t + a i 2 s i 2 t 2 / 2 ) i =1 n
luego Y se distribuye normalmente con media
å a i mi y varianza
i =1 n
2
2 a i s i å
i =1 Uno de los resultados mas importantes de este teorema esta relacionado con la demostración del teorema del limite central pero antes recordemos: Si tenemos que X 1 , X 2 ,…, X n n variables aleatorias independientes e idénticamente distribuidas con una distribución de probabilidad no especificada donde E ( X i ) = m y Var ( X i ) = s 2 para todo i = 1, 2 ,..., n entonces X = X 1 + X 2 + ... + X n
X X X 1 n
= 1 + 2 + ... + n = å X i n n n n i =1 n Se define como la media muestral donde æ x 1 ö
æ x ö
æ x ö
÷ + E ç 2 ÷ + ... + E ç n ÷
è n ø
è n ø
è n ø
m X = E ( X ) = E ç
1
=
n m +
1 n m + ... +
1 n m = n m
=m
n y varianza
x ö
1 1 1 æ x 1 x 2 +
+ ... + n ÷ = 2 Var ( x 1 ) + 2 Var ( x 2 ) + ... + 2 Var ( x n ) n ø
n
n n è n n Var ( X ) = Var ç
= ns 2 s2
1
2 2 2 s
+
s
+
... +
s
=
= n 2 n 2 n (
Teor ema 4.2: ) Sean X 1 , X 2 ,…, X n n variables aleatorias independientes e idénticamente distribuidas con una distribución de probabilidad no especificada y que tiene una media
m y una varianza s 2 conocidos y finitos. Entonces X tiene una distribución con media
m y varianza s 2 / n que tiende hacia una distribución normal conforme n tiende a infinito. En otras palabras la variable aleatoria ( X - m ) /( s / n ) tiende como límite a una distribución normal estándar.
71 Demostr ación: Y =
Sean X - m
s / n y
Zi = X i - m
s
i = 1,2,3,…,n. Dado que.
n
X - m
n =1 1
i å
n i s / = 1 n å ( X i - m ) n s / n i =1 1
1 é n n
ù
X i -n m ú
å
ê
n s / n ë n i =1 û
1
=
n
1 é n
ù
X i -å m ú
å
ê
n s / n ë i =1 i =1 û
1
=
= 1 1 n s / [n X - n m ]
n =
X - m
s / n Luego Y = 1
n
X - m
n n X i - m
= = å
n i =1 s
n =1 i å
n i s / 1 n
å Z i n i =1 ahora usando el teorema n M Y (t ) = M 1 n
å Z i ( t ) = Õ M Z (t / i [
] [
n ] n ) = M Z i (t / n ) = E (exp( Z i t / n ) n i =1 dado que las Z i son variable aleatorias independientes al expandir exp( Z i t / n ) en una serien de Taylor exp( Z i t / n ) = 1 +
= 1 +
Z i t Z i 2 t 2 Z i 3 t 3 Z i 4 t 4 +
+ 2 / 3 +
+ ... 24 n 2 n 2 n 6 n t t 2 2 t 3 t 4 Z i +
Z i + 2 / 3 Z i 3 +
Z 4 + ... 2 i 2 n 6 n 24 n n si se toman los valores esperados
[
] E exp( Z i t / n ) = 1 +
t t 2
t 3 t 4 E ( Z i ) +
E ( Z i 2 ) + 2 / 3 E ( Z i 3 ) +
E ( Z i 4 ) + ... 2 2 n 6 n 24 n n 72 Recordemos que por ser normal E ( Z i ) = 0 y Var ( Z i ) = E ( Z i 2 ) - E 2 ( Z i ) = 1 Þ E ( Z i 2 ) - 0 = 1 Þ E ( Z i 2 ) = 1 luego
[
] E exp( Z i t / n ) = 1 +
t 2
t 3 t 4 + 2 / 3 E ( Z i 3 ) +
E ( Z i 4 ) + ... 2 n 6 n 24 n 2 entonces é t 2 ù
t 3 t 4 M Y (t ) = ê1 +
+ 2 / 3 E ( Z i 3 ) +
E ( Z i 4 ) + ... ú
2 24 n ë 2 n 6 n û
n ì 1 é t 2 ùü
t 3 t 4 = í1 + ê +
E ( Z i 3 ) +
E ( Z i 4 ) + ... ú ý
2 / 3 24 n ûþ
î n ë 2 6 n sea u = t 2
t 3 t 4 E ( Z i 3 ) +
E ( Z i 4 ) + ... 2 / 3 2 6 n 24 n +
æ uö
M Y (t ) = ç1 + ÷
è n ø
n ahora æ uö
lim M Y ( t ) = lim ç1 + ÷
n ® ¥
n ® ¥è
n ø
æ
n ® ¥
è
y por definición lim ç 1 +
n n uö
u ÷ = e n ø
luego
73 n lim M Y ( t ) =
n ® ¥
é t 2 ù
t 3 t 4 exp ê + E ( Z i 3 ) +
E ( Z i 4 ) + ... ú
2 / 3 24 n ë 2 6 n û
con lo cual queda demostrado que a medida de que n crezca Y =
una distribución normal estándar.
74
(
) = exp t 2 / 2 X - m
va a tender a s / n APÉNDICE Deducción de la función Gamma: La función Gamma esta definida por: ¥
G ( n ) = ò u n -1 e -u du n > 0 0 ahora veamos que G ( n) = ( n - 1 )! ¥
G ( n ) =
n -1 - u ò u e du 0 si z = u n -1 Þ dz = ( n - 1 ) u n -2 dv = e - u du Þ v = -e -u ¥
¥
¥
G ( n ) = - e -u u n -1 + ( n - 1 ) ò u n -2 e -u du = ( n - 1 ) ò u n -2 e -u du 0 0 0 z = u n -2 Þ dz = ( n - 2 ) u n -3 dv = e -u du Þ v = -e - u ¥
¥
é
ù
¥
G ( n ) = ( n - 1 ) ê- e - u u n -2 + ( n - 2 ) ò u n -3 e -u du ú = ( n - 1 )( n - 2 ) ò u n -3 e -u du 0 0 0 ë
û
75 z = u n -3 Þ dz = (n - 3 ) u n -4 dv = e - u du Þ v = -e - u ¥
é
ù
¥
G ( n ) = ( n - 1 )( n - 2 ) ê- e - u u n -3 + ( n - 3 ) ò u n -4 e -u du ú
0 0 ë
û
¥
= ( n - 1 )( n - 2 )( n - 3 ) u n -4 e -u du ò
0 y si seguimos la secuencia tendríamos
¥
G ( n ) = ( n - 1 )( n - 2 )( n - 3 )...( 3 )( 2 )( 1 ) ò u n -n e -u du 0 = (n - 1 )( n - 2 )( n - 3 )...( 3 )( 2 )( 1 )( 1 ) = (n - 1 )! ahora mostremos las propiedades
· G ( n + 1 ) = n ! Si reemplazamos a n por n­1 tendríamos que. G (n + 1 ) = ( n + 1 - 1 )! ósea que G ( n + 1 ) = ( n )! · G (n + 1 ) = n G ( n ) Por la propiedad anterior tenemos que G ( n + 1 ) = n ! = n (n - 1 )! = nG(n ) ·
G ( 1 / 2 ) = p
¥
G ( 1 / 2 ) = ò u -1 / 2 e -u du n > 0 0 76 ahora si u =
z 2 Þ du = 2 zdz luego
¥
¥
G ( 1 / 2 ) = ò z -1 e - z
2 2 2 zdz = 2 ò e - z dz =
0 0 2 p
= 2 p
Deducción de la función Beta: La función Beta esta definida por. 1 B( a , b ) = ò xa -1 ( 1 - x ) b -1 dx a , b > 0 0 £ x £ 1 0 mostremos que se encuentra relacionada con la función Gamma por G (a ) G( b ) B (a , b ) = G ( a + b ) 1 B (a
, b ) = ò xa -1 ( 1 - x ) b -1 dx 0 si u = (1 - x ) b -1 Þ du = -( b - 1 )( 1 - x ) b -2 dx dv = x a -1 du Þ v =
1 x a a
1 xa ( 1 - x ) b -1 b - 1 a
b - 2 B (a
, b ) =
+
ò0 x ( 1 - x ) dx a
a
0 b - 1 1 a
=
x ( 1 - x ) b -2 dx ò
a 0 u = (1 - x ) b - 2 Þ du = -( b - 2 )( 1 - x ) b -3 dx dv = x a du Þ v =
x a +1
a + 1 77 1 ù
b - 1 é xa + 1 ( 1 - x ) b -2 b - 2 1 a +1 ê
+
x ( 1 - x ) b -3 dx ú
ò
a ê
a + 1 a + 1 0 ú
0 B(a
, b ) =
ë
û
1 ( b - 1 )( b - 2 ) a +1 x ( 1 - x ) b -3 dx ò
a ( a + 1 ) 0 =
u = (1 - x ) b -3 Þ du = -( b - 3 )( 1 - x ) b -4 dx dv = x a +1 du Þ v =
x a + 2
a + 2 1 ù
( b - 1 )( b - 2 ) é xa + 2 ( 1 - x ) b -3 b - 3 1 a + 2 b - 4 ê
ú
B(a
, b ) =
+
x ( 1 x ) du a ( a + 1 ) ê
a + 2 a + 2 ò0 úû
0 ë
1 ( b - 1 )( b - 2 )( b - 3 ) a + 2 x ( 1 - x ) b - 4 du a ( a + 1 )( a + 2 ) ò0 =
y si seguimos la secuencia tendríamos que
1 ( b - 1 )( b - 2 )( b - 3 ) B (a , b ) =
... ò xa + b -2 ( 1 - x ) b - b du a ( a + 1 )( a + 2 ) 0 1 ( b - 1 )( b - 2 )( b - 3 ) ... ò xa + b -2 du a ( a + 1 )( a + 2 ) 0 =
1 ( b - 1 )( b - 2 )( b - 3 ) x a + b -1 = ... a ( a + 1 )( a + 2 ) a + b - 1 0 = ( b - 1 )( b - 2 )( b - 3 ) 1 ... a ( a + 1 )( a + 2 ) a + b - 1 G( b ) a ( a + 1 )( a + 2 )... a + b - 1 = 78
= (a - 1 )! G ( b ) ( a - 1 )! a ( a + 1 )( a + 2 )... a + b - 1 = G (a ) G ( b ) G( a + b ) Propiedades básicas de las distribuciones discretas Distribución uniforme: f ( x ) = n
1 x = 1, 2 ,... n n n=1,2,3,…
1
m x (t ) = å e it i =1 n m =
n + 1
2 s 2 = ,
n 2 - 1 12 , a 4 = a 3 = 0 , 9 n 2 - 21 240 n 2 - 240 Distribución bernoulli: f ( x ) = p x q 1 - x 0 £ p £ 1 x = 0, 1 m x (t ) = q + pe t m = p , s 2 = pq , a 3 = q - p , pq Distribución binomial
79 a 4 = -3 +
1 pq x = 1, 2 ,..., n 0 £ p £ 1 n = 1 , 2 , 3 ... æ n ö
f ( x ) = çç ÷÷ p x q n - x è x ø
m x (t ) = (q + pe t ) , n m = np , s 2 = npq , a 3 = q - p , npq a 4 = 3 +
1 - 6 pq npq Distribución hipergeométrica
x = 0, 1 , 2 ,..., n N = 1 , 2 , 3 ,... K = 1 , 2 ,..., N n = 1 , 2 , 3 ,..., N æ k öæ N - K ö
çç ÷÷çç
÷
x øè n - x ÷ø
è
f ( x ) = æ N ö
çç ÷÷
è n ø
m=
nk
,
N a 4 =
s 2 = nk ( N - k )( N - n ) , n 2 ( N - 1 ) a 3 =
( N - 2 k )( N - 2 n )( N - 1 ) 1 / 2 ( N - 2 )[ nk ( N - k )( N - n )] 1 / 2 N 2 ( N - 1 ){ N ( N + 1 ) - 6 n ( N - n ) + 3 k ( N - k )[ N 2 ( n - 2 ) - Nn 2 + 6 n ( N - n )] / N 2 } ( N - 2 )( N - 3 ) nk ( N - k )( N - n ) Nota: debe anotarse que la función generadora de momentos de la distribución hipergeométrica es demasiado tediosa de trabajar, por esto no es usada. Distribución poisson
80
f ( x ) = M
X [ (
e - l l x
x ! x = 0, 1 , 2 ,.... l>0
)] ( t ) = exp l e t - 1 ,
s 2 = l ,
m =l,
a 3 =
1 l
a 4 = 3 +
,
1 l
Distribución geométrica f ( x ) = pq x x = 0, 1 , 2 ,... , 0 < p £ 1 , p = 1 - q p ,
1 - qe t M X ( t ) = m =
q ,
p q , p 2 s 2 = a3 =
p ( 1 + q ) , q a 4 = 7 + q +
1 q Distribución binomial negativa æ r + x - 1 ö r x ÷ p q x ÷ø
è
x = 0, 1 , 2 ,... f ( x ) = çç
81
0 < p £ 1 r > 0
r æ p ö
÷ ,
M X ( t ) = çç
t ÷
è 1 - qe ø
m =
rq ,
p s 2 = rq , p 2 a 3 =
2 - p
, k ( 1 - p ) a 4 = 3 +
p 2 - 6 p + 6 k ( 1 - p ) Propiedades básicas de las distribuciones continuas Distribución uniforme f ( x ) = m x (t ) = m =
a < x < b - ¥ < a < b < ¥
1 b - a e bt - e at ,
(b - a ) t a + b ,
2 s 2 = ( b - a ) 2 , 12 a 3 = 0 , a 4 = 9 / 5 Distribución normal
é 1 æ x - m ö 2 ù
f ( x ) = exp ê- ç
÷ ú
2 ps ëê 2 è s ø ûú
1 - ¥ < x < ¥
é
ë
1 2 ù
û
M X (t ) = exp êm t + s 2 t 2 ú
a 3 = 0 , a 4 = 3 82 ¥<m<¥
s >0
Nótese que
m y s 2 son parámetros de la función. Distribución Beta 0 < x < 1 1 f ( x ) =
x a -1 ( 1 - x ) b -1 B ( a , b ) m=
a
,
a + b a4 =
s 2 = ab
2 ( a + b + 1 )( a + b ) a > 0 b > 0 a 3 =
2 ( b - a ) a + b + 1 ab ( a + b + 2 ) 3 ( a + b + 1 )[ 2 ( a + b ) 2 + ab ( a + b - 6 )] ab ( a + b + 2 )( a + b + 3 ) Nota: La función generadora de momentos de la distribución Beta no tiene una forma sencilla de trabajar por esto no se utiliza. Distribución Weibull f ( x ) =
a a -1
x exp[ - ( x / q ) a ] qa
- t æ t ö
M X (t ) = a b Gç1 + ÷
è b ø
æ
è
m = qGç1 +
1 ö
÷,
aø
é æ
ë è
s 2 = q 2 êGç1 +
2 ö
1 öù
2 æ
÷ - G ç1 + ÷ú
aø
è a øû
a 3 = G(1 + 3 / a ) - 3 G ( 1 + 1 / a ) G( 1 + 2 / a ) + 2 G 3 ( 1 + 1 / a ) [ G( 1 + 2 / a ) - G 2 ( 1 + 1 / a )] 3 / 2 a 4 =
G(1 + 4 / a ) - 4 G( 1 + 1 / a ) G( 1 + 3 / a ) 6 G 2 ( 1 + 1 / a ) G ( 1 + 2 / a ) - 3 G 4 ( 1 + 1 / a ) +
[ G( 1 + 2 / a ) - G 2 ( 1 + 1 / a )] 2 [ G( 1 + 2 / a ) - G 2 ( 1 + 1 / a )] 2 83 Distribución Gamma
f ( x ) = 1 x a -1 e - x / q
G( a ) q a
x > 0, a , b > 0 M X ( t ) = ( 1 - q . t ) a
m = aq ,
s 2 = aq 2 ,
a 3 =
2 a
æ
è
a 4 = 3 ç1 +
,
2 ö
÷
aø
Distribución exponencial La función gamma en la que a = 1 se llama distribución exponencial.
1 f ( x ) = e - x / q
q x > 0, b > 0 M X (t ) = 1 - q . t m =q ,
s 2 = q 2 , a 4 = 9 a 3 = 2 , Distribución Chi­cuadrado La función gamma en la que a = v / 2 y q = 2 se llama distribución Chi­cuadrado. Donde v es un entero positivo y se denomina grados de libertad de la variable. V / 2 1 æ 1 ö
f ( x ) = ç ÷
G( V / 2 ) è 2 ø
M X ( t ) = ( 1 - 2 . t ) v / 2 84 x V / 2 -1 e - x / 2 m = v ,
s 2 = 2 v , a3 =
4 2 v æ
4 ö
a 4 = 3 ç1 + ÷
è v ø
,
Distribución Cauchy 1 f ( x ) = pb { 1 + [( x - a ) / b ] 2 } Esta distribución tiene la particularidad de no tener media, porque E ( x ) no converge, y por tanto no existe ningún momento, ni la función generadora de momentos.
85 CONCLUCIONES
·
La función generadora de momentos es directamente aplicable al descubrimiento de la distribución de probabilidad de sumas de variables aleatorias.
·
Hallar una función generadora de momentos de una variable Y = g ( X ) asegura el conocimiento de una distribución de probabilidad única.
·
El cálculo integral es una buena herramienta para apoyar la función generadora de momentos.
·
Este trabajo intenta motivar el estudio de escenarios específicos, donde las matemáticas son útiles.
86 BIBLIOGRAFÍA
·
WALPOLE Ronald, MEYERS Raymond.2005. Probabilidad y estadística. Mc Graw Hill.
·
CANAVOS George. Probabilidad y estadística aplicaciones y métodos. Mc Graw Hill.
·
HOGG Robert. Introduction to mathemátical. Collier Macmillan publishers.
·
MOOD, GRAYBILL, BOES. introduction to the theory of statistics, Mc Graw Hill.
·
http://www.pokertips.com.es/strategy/expected­value.php
·
http://www.personal.us.es/olmedo/El%20concepto%20de%20Valor%20Esperado.pd
87