Ejemplo, En una pregunta del CIS sobre la edad hasta la que
Anuncio

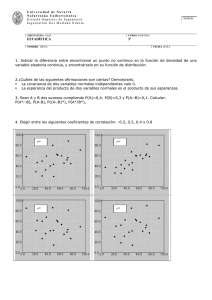
LECCIÓN 22. FUNCIÒN DE DISTRIBUCIÓN NORMAL Ejercicio. El parque está formado por 50 torres numeradas de 1 a 50. Denotamos por X 1, X2, X50 las potencias producidas por cada una de las torres en un momento dado. Supongamos que cada X i sigue una distribución Normal con media 1000 y varianza 2500. a). ¿Cuál es la probabilidad de que la potencia producida por una torre sea mayor que 1050 unidades? b). Suponiendo que las variables X1, ,X50 son independientes, ¿cuál es la probabilidad de que haya exactamente 8 torres que estén produciendo mas de 1050 unidades? c). Calcular la probabilidad de que mas de 10 torres estén produciendo mas de 1050 unidades. d). Si P es la potencia total producida por el parque en un momento dado, y si seguimos suponiendo que las variables X1, ,X50 son independientes, ¿cuál es la distribución de P? Ejemplo, La renta media de los habitantes de un país es de 4 millones de pesos/año, con una varianza de 1,5. Se supone que se distribuye según una distribución Normal. Calcular: a) Porcentaje de la población con una renta inferior a 3 millones de pesos. b) Renta a partir de la cual se sitúa el 10% de la población con mayores ingresos. c) Ingresos mínimo y máximo que engloba al 60% de la población con renta media. a) Porcentaje de la población con una renta inferior a 3 millones de pesos. z a) x4 1.22 El valor de z para 3 millones de pesos es de -0,816. P(X<3) = P(Z<-0,816) P (z>-0,816) = 1-P(z<0,816) = 1 - 0,7925 (aprox.) = 0,2075 Luego, el 20,75% de la población tiene una renta inferior a 3 millones pesos. b) Nivel de ingresos a partir del cual se sitúa el 10% de la población con renta más elevada. Vemos en la tabla el valor de la variable tipificada cuya probabilidad acumulada es el 0,9 (90%), lo que quiere decir que por encima se sitúa el 10% superior. Ese valor corresponde a z=1,282. Ahora calculamos la variable normal x equivalente a ese valor de la normal tipificada: 1.282=(x-4)/1.22 Despejando x=5,57. Por lo tanto, aquellas personas con ingresos superiores a 5,57 millones de pesos constituyen el 10% de la población con renta más elevada. c) Nivel de ingresos mínimo y máximo que engloba al 60% de la población con renta media. Vemos en la tabla el valor de la variable normalizada Y cuya probabilidad acumulada es el 0,8. Como sabemos que hasta la media la probabilidad acumulada es del 50%, quiere decir que entre la media y este valor de z hay un 30% de probabilidad. Por otra parte, al ser la distribución normal simétrica, entre -z y la media hay otro 30% de probabilidad. En definitiva, el segmento (-z,z) engloba al 60% de población con renta media. El valor de z que acumula el 80% de la probabilidad es 0,842 (aprox.), por lo que el segmento viene definido por (-0,842, +0,842). Ahora calculamos los valores de la variable x correspondientes a estos valores de z. Los valores de x son 2,97 y 5,03. Por lo tanto, las personas con ingresos superiores a 2,97 millones de pesos e inferiores a 5,03 millones de pesos constituyen el 60% de la población con un nivel medio de renta. Ejercicio. Se está investigando el tiempo de aguante de unas baterías recargables. Por estudios anteriores, se sabe que la distribución de los tiempos de aguante es aproximadamente normal con una desviación típica de 8mn. Se diseña un experimento en el que se mide el tiempo de aguante para 10 baterías, y se encuentra una media de 121 minutos. a). Construir detalladamente un intervalo de confianza al 95% de confianza para el tiempo promedio de aguante de una batería. b). ¿Se puede afirmar al 95% de confianza que el tiempo promedio de aguante es mayor de 115mn? Calcular el p-valor asociado a la prueba. c). ¿Cuántas baterías deberían probarse en el experimento si queremos asegurarnos que, con una confianza de 95%, el margen de error cometido no será mayor que 4mn? d). Planeamos contrastar, con 95% de confianza y una muestra de 10 baterías, la hipótesis de que el tiempo promedio de aguante es igual a 115mn. ¿Cuál es la potencia del test contra la alternativa µ = 120 ? ¿Te parece suficiente? ¿Como se podría mejorar? Ejemplo. La vida media de los habitantes de un país es de 68 años, con una varianza de 25. Se hace un estudio en una pequeña ciudad de 10.000 habitantes: a) ¿Cuántas personas superarán previsiblemente los 75 años? b) ¿Cuántos vivirán menos de 60 años? a) Personas que vivirán (previsiblemente) más de 75 años Calculamos el valor de la normal tipificada equivalente a 75 años: z=(75-68)/5= 1.40 Por lo tanto, P (x>75) = (z>1,4) = 1 - P (z<1,4) = 1 - 0,9192 = 0,0808 Luego, el 8,08% de la población (808 habitantes) vivirán más de 75 años. b) Personas que vivirán (previsiblemente) menos de 60 años Calculamos el valor de la normal tipificada equivalente a 60 años, z=(60-68)/5=1.60 Por lo tanto P (x<60) = (z< -1,6) = P(z> 1,6) = 1 - P (z<1,6) = 0,0548 Luego, el 5,48% de la población (548 habitantes) no llegarán probablemente a esta edad. La función característica de la distribución normal y sus parámetros son Z ( t ) e itz E ( X) 1 e z 2 /2 2 V( X) 2 x ( t ) e it( t 2 2 / 2) siendo z x Ejemplo, En una pregunta del CIS sobre la edad hasta la que consideran convenientes los padres controlar los programas y el tiempo de televisión de los hijos, la media fue de 15,4 años y la desviación típica de 2,11. Teniendo en cuenta que las respuestas se distribuyen aproximadamente como la curva normal y que van de los 7 a los 24 años, calcular: a)-Cuantos respondieron que la edad debe ser hasta los 13 años b)-Cuantos dijeron que debe estar entre 14 y 17 años. c)-Cuantos respondieron que debe estar por encima de los 19 años a) x 15,4 Sx = 2,1 z x x 13 15,4 1,13 Sx 2,11 Consultando las tablas de la curva normal comprobamos que entre la media y un desviación típica de 1,13 encontramos un área de 0,3708 que si situaría a la izquierda de la curva por tener signo negativo. Si el área que queremos calcular es el que queda a la izquierda del valor -1,13, es decir, los de menos de 13 años, restamos a 0,5 (que es la superficie de la mitad de la curva) 0,3708 y obtenemos el resultado de 12,92% 0,5-0,3708= 0,1292 b) z1 x x 14 15,4 0,66 Sx 2,11 z2 x x 17 15,4 0,75 Sx 2,11 Las áreas correspondientes a estos valores z son 0,2454 y 0,2734 respectivamente. Como en este caso nos preguntan por el área comprendida entre las unidades z –0,66 y 0,75 sumaremos ambas con el resultado de del 51,88% 0,2454+0,2734 = 0,5188 z x x 19 15,4 1,70 S 2,11 c) El área correspondiente es de 0.4554 y los que están por encima de 1,7 unidades z se obtienen restando de 0,5, el 0,4554 de las tablas. 0,5-0,4554 = 0,0446, es decir el 4,46%. Ejemplo, Supongamos que cierto fenómeno pueda ser representado mediante una variable aleatoria X N(45,9) , y queremos calcular la probabilidad de que X tome un valor entre 39 y 48, es decir, P(39 X 48) Solución, hallamos la variable estandarizada 39 45 48 45 0.666 y z2 0.333 de modo que 9 9 P(39 X 48) P(0.666 Z 0.333) 0.378 z1 Remitimos al lector a la tabla de la función de distribución Normal para evaluar los valores de la función acumulada, que se anexan a este capítulo Ejemplo, Durante cierta epidemia de gripe, enferma el 30% de la población. En un aula con 200 estudiantes, Cuál es la probabilidad de que al menos 40 de ellos padezcan la enfermedad? y Calcular la probabilidad de que haya 60 estudiantes con gripe. Solución: La variable aleatoria que contabiliza el número de alumnos que padece la gripe es X B(200,0.30) cuya media es np=60 y varianza es npq=42. Realizar los cálculos con la Binomial es muy engorroso, ya que intervienen números combinatorios de gran tamaño, y potencias muy elevadas. Por ello utilizamos la aproximación normal de X, teniendo en cuenta que se verifican las condiciones necesarias para que el error sea aceptable: n=200>30, np=60>4, y nq=140>4, entonces X N(60, 42) Así aproximando la variable aleatoria discreta binomial X, mediante la variable aleatoria continua normal, X 60 40 60 P(X 40) P P( Z 3.09) 42 42 en las tablas: P 0.999 También es necesario calcular P(X=60). Esta probabilidad se calcula exactamente como: 200 60 140 * p * q P(X 60) 60 o f (60) 1 2 e 1 60 2 2 0.063 Ejemplo, Los resultados de una prueba objetiva de selección pasada a 200 personas indicaron que la distribución de puntuaciones era normal, con media 60 puntos y desviación típica de 6 puntos. Cada prueba se puntuó con 0 ó 1 puntos. Calcular cuántos examinados han obtenido una puntuación entre 30 y 40 puntos, y cuál es la mínima puntuación por debajo de la cual están el 75 % de los examinados. Tipifiquemos la variable con los valores extremos dados: 30 60 5 6 40 60 z2 3,33 6 z1 La probabilidad de obtener una puntuación entre 30 y 40 es: p(30 X 40) p(5 z 3,33) p(3,33 z 5) p( z 5) p( z 3,33) 1 1 0 con lo cual no hay ningún examinado con una puntuación entre 30 y 40. Por otro lado, la mínima puntuación por debajo de la cual está el 75 % de los examinado la obtenemos así: para 0,67 0,7486 p( z z x ) 0,75 z x para 0,68 0,7517 El valor de zx está entre 0,67 y 0,68 podemos realizar una interpolación proporcional para obtener: Para 0,01, la diferencia es 0,0031 Para x, la diferencia es 0,0014 luego: x 0,0014 0,01 0,0045 0,0031 entonces: zx=0,67+0,0045=0,6745 x1=6zx+60=6 . 0,6745+60=64 Y la mínima puntuación por debajo de la cual está el 75 % de los examinados es 64. Ejemplo, Una empresa instala en una ciudad 20.000 bombillas para su iluminación. La duración de una bombilla sigue una distribución normal con media 302 días y desviación típica 40 días. ¿Cuántas bombillas es de esperar que se fundan antes de 365 días? ¿Cuántas durarán más de 400 días? Explica razonadamente el método seguido par encontrar la solución. 365 302 1,575 40 Tipificamos el valor 365: entonces: p( X 365) p( z 1,575) 0,9418 siendo la esperanza matemática: E= n.p= z 20000 . 0,9418 = 18836 bombillas se fundirán antes de 365 días. Tipifiquemos el valor 400: z1 400 302 2,45 40 entonces: p( X 400) p( z 2,45) 1 p( z 2,45) 1 0,9929 0,0071y la esperanza matemática: E=20000 . 0,0071 = 142 bombillas durarán más de 400 días. Ejemplo, Explica el significado de la expresión “LA BINOMIAL COMO APROXIMACIÓN A LA NORMAL”. Considera tres distribuciones binomiales B(10; 0,1), B(200; 0,1) y B(200; 0,5) y explica cuál de ellas se puede aproximar mejor y cuál peor por una distribución normal. Una distribución binomial se puede aproximar por una normal de media m = np y desviación típica s npq siempre que n tienda a infinito (en la práctica es suficiente que n sea mayor o igual que 30) y p sea muy próximo a 0,5. La aproximación es muy buena cuando np y nq son superiores a 5. En las tres binomiales dadas: B(10;0,1) m np 1 s npq 10 0,1 0,9 0,95 B(200;0,1) m 200 0,1 20 B(200;0,5) m 200 0,5 100 s 200 0,1 0,9 4,24 s 200 0,5 0,5 7,07 Siendo la mejor aproximación la última pues en ella n=200>300 y p=0,5 con np=nq=100>5 La peor es la primera pues n=10<30 y p=0,1 siendo np=1 inferior a 5 y nq=10.0,9=9 Ejemplo, Explica qué es una distribución de probabilidad de variable continua. Como ejemplo describe la ley de distribución normal. Suponiendo que las tallas de los adultos de un país A siguen una distribución normal con media 180 cm. y desviación típica 5 cm. y que las tallas de los adultos en un país B siguen una distribución también normal, pero con media 180 cm. y desviación típica 15 cm., contestar razonadamente en cuál de los dos países es más probable encontrar adultos con talla superior a 195 cm. y dónde es más probable encontrar adultos con talla comprendida entre 175 y 185 cm. Una variable aleatoria continua es aquélla que puede tomar todos los valores reales comprendidos en un intervalo. Su distribución de probabilidad es la expresión que asigna a cada valor de la variable su correspondiente probabilidad. La distribución normal es una variable aleatoria continua en la cual mediante la expresión (función de distribución): x p( X x) s 1 2 e ( xm)2 2s2 dx calculamos la probabilidad de que un determinado valor X sea menor o igual que otro dado x. Y la expresión: f ( x) 1 s 2 e ( xm)2 2s2 es la función de densidad que da los valores de las probabilidades de que X tome un valor fijo x. A la distribución normal de media m y desviación típica s la representamos abreviadamente por N(m,s), y su función densidad tiene las siguientes propiedades: - Presenta un máximo en X=m - La recta y=0 es una asíntota horizontal. - - El área encerrada por la curva de la función y el eje OX es 1. Presenta puntos de inflexión en m+s(decreciente) y en m-s(creciente. Su dominio es R. Es simétrica con relación al eje OY Es siempre positiva. Gráficamente la función f(x) presenta el siguiente aspecto: Donde se ha representado la distribución normal N(0,1), esto es, con m=0 y s=1. Elegido un punto cualquiera del eje OX, su ordenada correspondiente nos da el valor de la probabilidad de que la variable independiente tome ese valor concreto. En el problema planteado, empezaremos tipificando el valor 195 en ambas distribuciones: 195 180 3 5 195 180 z2 1 15 z1 En la primera, la probabilidad de que un adulto tenga talla superior a 195 cm es: p( X 195) p( z 3) 1 p( z 3) 0 Y en la segunda: p( X 195) p( z 1) 1 p( z 1) 1 0,8413 0,1587 luego es más probable encontrar un individuo de la talla dada en la 2ª. Tipifiquemos ahora los valores 175 y 185 en ambas distribuciones: 175 180 175 180 1 z1 ' 0,33 5 15 185 180 185 180 z2 1 z2 ' 0,33 5 15 z1 y las probabilidades son: p(175 X 185) p(1 z 1) p( z 1) p( z 1) 2 p( z 1) 1 2 0,8413 1 0,6826 p(175 X 185) p(0,33 z 0,33) 2 p( z 0,33) 1 2 0,6293 1 0,2586 luego es más probable encontrar individuos de tallas comprendidas entre 175 cm. y 185 cm. en la primera distribución. Ejemplo, El peso de los adultos de una población numerosa se distribuye normalmente con media 65 kg. y desviación típica 3 kg. Se eligen dios individuos al azar. Calculando las correspondientes probabilidades, justifica qué es más probable: a) Que cada uno de los individuos tenga un peso comprendido entre 63,5 y 66,5 kg. b) Que uno de ellos tenga un peso comprendido entre 62 y 68 kg. y el otro tenga un peso no comprendido entre 62 y 68 kg. Tipifiquemos los valores que nos han proporcionado: 63,5 65 0,5 3 66,5 65 z2 0,5 3 62 65 z3 1 3 68 65 z4 1 3 z1 La probabilidad de que un individuo tenga un peso comprendido entre 63,5 y 66,5 es: p(63,5 X 66,5) p(0,5 z 0,5) p( z 0,5) p( z 0,5) p( z 0,5) p( z 0,5) p( z 0,5) 1 p( z 0,5) 2 p( z 0,5) 1 2 0,6915 1 0,383 y la de que ambos estén en ese intervalo es: 0,383 . 0,383 = 0,147 Por otro lado, la probabilidad de que uno esté entre 62 y 68 es: p(62 X 68) p(1 z 1) p( z 1) p( z 1) p( z 1) 1 p( z 1) 2 p( z 1) 1 2 0,8413 1 0,6826 y la de que el otro no esté en ese intervalo es: p( X 62,68) p( z 1,1) 1 0,6826 0,3174 y la de que las dos cosas ocurran simultáneamente es: 0,6826 . 0,3174 = 0,2167 Luego es más probable lo que se indica en el apartado b) que lo que se indica en el a). Ejemplo, Explica qué es una distribución de probabilidad normal. Supón que x e y representan la talla de ,los adultos de dos ciudades, que supondremos que se distribuyen normalmente con medias 168 y 171 cm. y desviaciones típicas de 2 y 1 cm. respectivamente. Justifica, sin recurrir a tablas, que la probabilidad de que x esté comprendida entre 166 y 170 cm. coincide con la probabilidad de que y esté comprendida entre 170 y 172 cm. Para el concepto de distribución de probabilidad normal ver ejercicio nº 4 de este mismo capítulo. Si tipificamos los datos proporcionados para las variables x e y tendremos: x 168 166 168 1 2 2 y 171 z2 170 171 1 1 z1 y 170 168 1 2 y 172 171 1 Y, como los valores tipificados de los extremos de cada uno de los intervalos dados son iguales, se cumplirá: p(1 z1 1) p(1 z 2 1) p(166 X 170) p(170 y 172) como se quería demostrar. Ejemplo, La estatura de una población se distribuye normalmente con media 170 cm. y desviación típica 6 cm. Calcular la probabilidad de que, elegido un individuo al azar, tenga estatura comprendida entre 158 y 182 cm. Tipificamos los extremos del intervalo: 158 170 2 6 182 170 z2 2 6 z1 Con lo que la probabilidad pedida será: p(158 X 182) p(2 z 2) p( z 2) p( z 2) p( z 2) 1 p( z 2) 2 p( z 2) 1 2 0,9772 1 0,9544 Ejemplo, Los resultados de una prueba objetiva de selección pasada a 200 personas indicaron que la distribución de puntuaciones era normal, con media de 80 puntos y desviación típica de 6 puntos. Calcular cuántos examinados han obtenido una puntuación entre 70 y 90 puntos. Si se eligen al azar dos de esas 200 personas, calcular la probabilidad de que ambas personas tengan puntuación superior a 90. Tipificamos: 70 80 1,67 6 90 80 z2 1,67 6 z1 La probabilidad de obtener puntuación entre 70 y 90 es: p(70 X 90) p(1,67 z 1,67) p( z 1,67) p( z 1,67) p( z 1,67) 1 p( z 1,67) 2 p( z 1,67) 1 2 0,9525 1 0,905 y el número esperado de individuos que la obtienen es: n= 0,905 . 200 = 181 La probabilidad de que una persona tenga puntuación superior a 90 es: p( X 90) p( z 1,67) 1 p( z 1,67) 1 0,9525 0,0475 Y para dos personas: p= 0,0475 . 0,0475 =0,0023 Ejemplo, Los ingresos diarios de una empresa tienen una distribución normal con media 35560 ptas. y desviación típica 2530 ptas. Justifica si es o no razonable el esperar obtener un día unas ventas superiores a 55000 ptas.. Calcular cuántos días en un año se espera obtener unas ventas superiores a 40620 ptas. Tipificamos: 55000 35560 7,68 2530 40620 35560 z2 2 2530 z1 La probabilidad de obtener ventas superiores a 55.000 ptas. es. p( X 55000) p( z 7,68) 1 p( z 7,68) 1 1 0 luego no es razonable. La probabilidad de obtener ventas superiores a 40.620 ptas. es: p( X 40620) p( z 2) 1 p( z 2) 1 0,9772 0,0228 Lo que ocurrirá en: E= 365 . 0,0228 = 8,3 días al año. Ejemplo, Se sabe que las puntuaciones obtenidas al pasar un test siguen una distribución normal con media 210 puntos y desviación típica 0,6 puntos. Si se pasa el test a 100 personas, ¿Cuántas de esas 100 personas deberemos esperar que obtengan una puntuación entre 209 y 211 puntos? Tipificamos los extremos del intervalo: 209 210 1,67 0,6 211 210 z2 1,67 0,6 Y la probabilidad de que una persona obtenga puntuación entre 209 y 211 es: z1 p(209 X 211) p(1,67 z 1,67) p( z 1,67) p( z 1,67) 2 p( z 1,67) 1 2 0,9525 1 0,905 Con lo cual, la esperanza matemática para las 100 personas es: E= 100 . 0,905 = 90,5 personas estarán en el intervalo indicado. Ejemplo, Se sabe que dos poblaciones distintas X e Y se distribuyen normalmente con media 0. Además, p(X. Se pide que calcules sus respectivas varianzas. Indicaciones: Si Z es normal con parámetros 0, 1, entonces p(Z 1) 0,8413. Las variables tipificadas serán, llamando s1 y s2 a las respectivas desviaciones típicas: z1 2 s1 z2 3 s2 Entonces para las respectivas probabilidades se tiene: p( X 2) p(Y 3) 0,1587 p( z 2 1 p( z s ) 0,1587 p( z 1 3 1 p( z ) 0,1587 p( z s2 2 3 ) p( z ) 0,1587 s1 s2 2 ) 1 0,1587 0,8413 s1 3 ) 1 0,1587 0,8413 s2 Y de aquí se tiene, siguiendo la indicación dada en el enunciado, que: 2 1 s1 2 s12 4 s1 3 1 s 2 3 s 22 9 s2 que son las varianzas pedidas. Ejemplo, Las precipitaciones anuales en una región son, en media, de 2000 mm., con una desviación típica de 300 mm. Calcular, suponiendo distribución normal, la probabilidad de que en un año determinado la lluvia no supere los 1200 mm. Tipificamos para obtener: z 1200 2000 2,67 300 Y para la probabilidad pedida tenemos: p( X 1200) p( z 2,67) 1 p( z 2,67) 1 0,9962 0,0038 Ejemplo, Una variable aleatoria continua, tiene como función de densidad: f ( x) k x 2 x 0,1 para Calcular: a) El valor de la constante k. b) La varianza de dicha distribución. Para que se cumpla la condición de normalización, se tendrá: 1 kx 3 F ( x) kx dx 1 3 0 1 1 2 0 k 1 k 3 3 Y entonces la función densidad es: f(x)=3x2 Por otro lado vamos a calcular la media y la desviación típica, usando las definiciones: 1 m 0 1 3x 4 f ( x) xdx 3x dx 4 0 1 3 1 1 0 3 0,75 4 1 3 3x 9 s ( x m) 2 f ( x)dx ( x ) 2 3x 2 dx ( x 2 ) 3x 2 dx 4 2 16 0 0 0 1 3x 3 27x 2 3x 5 3x 4 27x 3 ( 3 x ) dx 0 2 16 5 8 48 1 4 0 3 3 27 189 63 0,7875 5 8 48 240 80 Y para la varianza tenemos: s2=0,78752=0,6202 Ejemplo, Se sabe que la talla media de la población en edad escolar es de 165 cm. con desviación típica de 12 cm. Un centro tiene 1400 alumnos matriculados: a) b) c) ¿Cuántos alumnos miden más de 155 cm.? ¿Qué proporción (%) de alumnos mide entre 150 y 178 cm.? Determinar la probabilidad de que un cierto alumno mida entre 170 y 185 cm. Tipificamos el valor 155 y da: z 155 165 0,83 12 Por tanto, la probabilidad de que un alumno mida más de 155 es: p( X 155) p( z 0,83) p( z 0,83) 0,7967 Cabe esperar, pues, que 0,7967 . 1400 = 1115 alumnos midan más de 155 cm. Tipificamos ahora los valores 150 y 178: 150 165 1,25 12 178 165 z2 1,08 12 z1 La probabilidad de que un alumno mida entre 150 y 178 cm. es: p(150 X 178) p(1,25 z 1,08) p( z 1,08) p( z 1,25) p( z 1,08) 1 p( z 1,25) p( z 1,08) p( z 1,25) 1 0,8599 0,8944 1 0,7543 Lo que supone un 75,43 % de los alumnos: Tipìficamos ahora los valores 170 y 185: 170 165 0,42 12 185 165 z2 1,67 12 z1 Y la probabilidad de que un alumno mida entre 170 y 185 cm. es: p(170 X 185) p(0,42 z 1,67) p( z 1,67) p( z 0,42) 0,9525 0,662 0,2897 __________________________________________________________________ Ejemplo, El peso de 600 alumnos se distribuye según una distribución normal N(67; 5). Calcula cuántos de ellos pesan: a) Más de 80 kg. b) Menos de 50 kg. c) Entre 50 y 80 kg. Tipificamos los valores 50 y 80 kg.: 50 67 3,4 5 80 67 z2 2,6 5 z1 La probabilidad de que un alumno pese más de 80 kg. es: p( X 80) p( z 2,6) 1 p( z 2,6) 1 0,9953 0,0047 Cabe esperar, por tanto, que: E 600 0,0047 2,82 3 alumnos pesen más de 80 kg. La probabilidad de que un alumno pese menos de 50 kg. es: p( X 50) p( z 3,4) p( z 3,4) 1 p( z 3,4) 1 1 0 y ningún alumno pesa menos de 50 kg. La probabilidad de que un alumno pese entre 50 y 80 kg. es: p(50 X 80) p(3,4 z 2,6) p( z 2,6) p( z 3,4) p( z 2,6) p( z 3,4) 1 0,9953 1 1 0,9953 Cabe esperar, pues que: E= 0,9953 . 600 = 597 alumnos pesen entre 50 y 80 kg. Ejemplo, Tras un test de cultura general se observa que las puntuaciones obtenidas siguen una distribución N(65; 18). Se desea clasificar a los examinados en tres grupos (de baja cultura general, de cultura general aceptable y de excelente cultura general) de modo que haya en el primero un 20 % de la población, un 65 % en el segundo y un 15 % en el tercero. ¿Cuáles han de ser las puntuaciones que marcan el paso de un grupo al otro? De los datos del problema se infiere que: p( z z1 ) 0,2 (1) p( z1 z z 2 ) 0,65 p( z z 2 ) 0,15 (2) (3) De (1) se deduce (al ser 0,2<0,5) que z1 es negativo, así que: p( z z1 ) p( z z1 ) 1 p( z z1 ) 1 0,2 0,8 z1 0,85 z1 0,85 x1 0,85 18 65 49,7 50 puntos De (2) se deduce que: p( z1 z z 2 ) p( z z 2 ) p( z z1 ) p( z z 2 ) 0,2 0,65 p( z z 2 ) 0,85 z 2 1,04 x2 1,04 18 65 83,7 84 Podemos, pues, tomar como notas de corte 50 y 84 puntos y afirmar que: Por debajo de 50 puntos tienen baja cultura general. Entre 50 y 84 puntos tienen cultura general aceptable. Por encima de 84 puntos tienen cultura general excelente. Ejemplo, La presión sanguínea de ciertos enfermos sigue una ley normal de media 90 mm. Hg y de desviación típica 12 mm. Hg. Hallar la probabilidad de que elegido un paciente al azar: a) Su presión sea mayor de 115 mm. Hg. b) Su presión esté comprendida entre 80 y 100 mm. Hg. Tipificando los valores 90, 80 y 100 tenemos: 115 90 2,08 12 80 90 z2 0,83 12 100 90 z3 0,83 12 z1 La probabilidad de que la presión sea mayor de 115 mm. Hg. es: p( X 115) p( z 2,08) 1 p( z 2,08) 1 0,9812 0,0188 Y la probabilidad de que la presión esté comprendida entre 80 y 100 mm. Hg: p(80 X 100) p(0,83 z 0,83) p( z 0,83) p( z 0,83) p( z 0,83) 1 p( z 0,83) 2 p( z 0,83) 1 2 0,7967 1 0,5934 Ejemplo, En una muestra de 1000 personas de una determinada población, resultó que la talla media era de 170 cm. con una desviación típica de 10 cm. Sabiendo que la talla se distribuye normalmente, calcula el número de personas que miden: a) Menos de 160 cm. b) Más de 2 m. Tipificamos los valores dados: 160 170 1 10 200 170 z2 3 10 z1 La probabilidad de medir menos de 160 cm. es: p( X 160) p( z 1) p( z 1) 1 p( z 1) 1 0,8413 0,1587 Por lo que cabe esperar que: E= 1000 . 0,1587 =158,7 159 personas midan menos de 160 cm. La probabilidad de medir más de 2 m. = 200 cm. es: p( X 200) p( z 3) 1 p( z 3) 1 1 0 Por lo que cabe esperar que nadie mida más de 2 m. Ejemplo, En una clase hay 15 alumnos y 20 alumnas. El peso medio de los alumnos es de 58,2 kg. y el de las alumnas 52,4 kg. Suponiendo que las desviaciones típicas de los dos grupos son, respectivamente, 3,1 kg. y 5,1 kg. El peso de Juan L. es 70 kg. y el de Pilar S. es 65 kg. ¿Cuál de ellos puede, dentro del grupo de alumnos de su sexo, considerarse más grueso? Tipificamos los valores dados dentro de cada sexo: 70 58,2 3,81 3,1 65 52,4 zP 2,47 5,1 zJ Como: p( z 3,81) p( z 247) pues 1 0,932 Se puede afirmar que Juan L. es igual de grueso que Pilar S. dentro de su grupo de sexo. Entre los chicos habrán 1 . 15 = 15 (todos) alumnos que pesan menos que Juan L. Entre las chicas habrán 0,9932 . 20 = 19,8 20 alumnas (todas) pesan menos que Pilar S. Luego, tanto Juan L. como Pilar S. son los más gruesos de su sexo. Ejemplo, Una persona A mide 1,75 m. y reside en una ciudad donde la estatura media es de 1,60 m. y su desviación típica es de 20 cm. Otra persona B mide 1,80 m. y vive en una ciudad donde la estatura media es de 1,70 m. y la desviación típica es de 15 cm. ¿Cuál de las dos será más alta respecto a sus conciudadanos? Tipificamos los valores dados: 175 160 0,75 20 180 170 zB 0,67 15 zA Como: p( z 0,75) p( z 0,67) pues 0,7734 0,7486 La probabilidad de medir en la primera ciudad menos de 175 cm es mayor que la de medir en la segunda menos de 180. Si ambas ciudades tuvieran el mismo número de habitantes, habria más ciudadanos en la 1ª con estaturas inferiores a la de A que en la 2ª con estaturas inferiores a la de B, por tanto A es más alto con relación a sus conciudadanos. Ejemplo, Las ventas de una determinada revista en un kiosko tienen de media 190 y una desviación típica de 25. ¿Cuántos ejemplares de la revista deben encargar para atender al 80 % de los clientes? Para que p=0,8, se ha de cumplir que: p( z z1 ) 0,8 z1 0,85 Con lo que se han de encargar: x= 0,85 . 25 + 190 = 211,25 revistas para atender al 80 % de los clientes. TEOREMA CENTRAL DEL LÍMITE Ejemplo, La variable tirar una moneda al aire sigue la distribución de Bernoulli. Si lanzamos la moneda al aire 50 veces, la suma de estas 50 variables (cada una independiente entre si) se distribuye según una distribución normal. Este teorema se aplica tanto a suma de variables discretas como de variables continuas. Los parámetros de la distribución normal son Media: n* (media de la variable individual multiplicada por el número de variables independientes), y Varianza: n* número de variables individuales) Ejemplo, Se lanza una moneda al aire 100 veces, si sale cara le damos el valor 1 y si sale Sello el valor 0. Cada lanzamiento es una variable independiente que se distribuye según el modelo de Bernoulli, con media 0,5 y varianza 0,25. Calcular la probabilidad de que en estos 100 lanzamientos salga más de 60 caras. La variable suma de estas 100 variables independientes se distribuye, por tanto, según una distribución normal. Media = 100 * 0,5 = 50 Varianza = 100 * 0,25 = 25 Para ver la probabilidad de que salgan más de 60 caras calculamos la variable normal tipificada equivalente z=(60-50)/5=2.0 Por lo tanto P(x>60) = P(z>2,0) = 1- P(z< 2,0) = 1 - 0,9772 = 0,0228 Es decir, la probabilidad de que al tirar 100 veces la moneda salgan más de 60 caras es tan sólo del 2,28% Ejemplo: Si asumimos que la resistencia de las baldosas se distribuye normalmente con y Resistencia de 100 Baldosas 1. 2. 3. 4. 5. 6. Si extraemos una baldosa al azar : Cual es la probabilidad de que: Resista menos de 448 Kg/cm2? Resista más de 588 Kg/cm2 ? Resista entre 308 y 588 Kg/cm2 ? Resista entre 168 y 728 Kg/cm2 ? Resista más de 600 Kg/cm2 ? Resista menos de 200 ó más de 700 Kg/cm2 ? Con la ayuda de los valores tabulados: CUESTIONARIO Y EJERCICIOS PROPUESTOS 1. La probabilidad de que un visitante efectúe una compra en un almacén, durante un día dado es 0.8. Si al negocio entran 20 clientes, ¿cuál es la probabilidad de que el almacén realice: 1.1 Exactamente 16 ventas? 1.2 Menos de 17 ventas? 1.3 Más de 14 ventas? 1.4 Exactamente 5 ventas? 1.5 ¿Cuál es el número esperado de ventas? 2. Si un almacén tiene en promedio 5 ventas por hora. ¿Cual es la probabilidad de que en una hora determinada: 2.1 Haya exactamente 4 ventas? 2.2 Haya más de 3 ventas? 2.3 No se efectúen ventas? 3. Una de cada 10 personas mayores de 40 años de una comunidad, sufren de hipertensión. Se toma una muestra de 50 personas mayores de 40 años. Utilizando primero la distribución binomial y luego la aproximación a la distribución de Poisson, responder y comparar los resultados: 3.1 ¿Cuál es la probabilidad que haya más de 4 hipertensos? 3.2 ¿Cuál es la probabilidad que haya exactamente 5 hipertensos? 4. Un lote de arandelas tiene un diámetro normal con media 10 milímetros y desviación típica 0.5 milímetros. Se toma una arandela al azar. ¿Cuál es la probabilidad de que tenga un diámetro: 4.1 4.2 Superior Entre 4.3 Menos de 9 milímetros? a 9 10.5 y 11 milímetros? milímetros?