tema 3: descripción numérica de variables cuantitativas

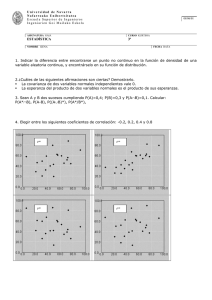
TEMA 3: DESCRIPCIÓN NUMÉRICA DE VARIABLES
CUANTITATIVAS (I)
● Hasta ahora hemos visto técnicas que permiten una
descripción de la distribución de una variable mediante
tablas y gráficos.
● La información sobre una variable puede resumirse de
forma más sencilla empleando valores numéricos que nos
den una idea de:
- ubicación o centro de los datos → medidas de posición
- concentración de observaciones alrededor del centro →
medidas de dispersión
- otros
rasgos
de
la
distribución
(asimetría,
apuntamiento…)
● En este tema veremos medidas de descripción numérica
que se construyen sumando cantidades.
1
La Media
● La media es una medida de posición (o de centralización)
que formaliza la idea intuitiva de centro de las
observaciones.
● La media de un conjunto de observaciones numéricas se
calcula sumando todos los valores y dividiéndolo por el
total de observaciones, es decir:
Dado un conjunto de observaciones:
x1 , x2 ,..., x N  1 , x N , la
media se representa como x y se calcula:
N
xi
x1  x2 ... x N 1  x N 
x
 i 1
N
N
2
Ejemplo:
Los salarios anuales (en euros) de los jefes de ventas de
una empresa pequeña son:
34.500
30.700
32.900
36.000
34.100
33.800
32.500
El salario medio de la plantilla de jefes de ventas será:
7
x  x  x3  x4  x5  x6  x7
x 1 2

7
x
i
i 1
7
es decir,
x
34.500  30.700  32.900  36.000  34.100  33800
.
 32.500
7
 33500
.
3
Propiedades de la media:
- La suma de las desviaciones de un conjunto de
observaciones respecto a su media es cero, es decir:
N
( x1  x )  ( x2  x ) ...( x N 1  x )  ( x N  x )   ( xi  x )  0
i 1
Ejemplo: Salarios
xi  x
34.500-33.500= 1.000
30.700-33.500=-2.800
32.900-33.500= -600
36.000-33.500= 2.500
34.100-33.500= 600
33.800-33.500= 300
32.500-33.500=-1.000
7
 (x
i
 x ) =0
i 1
4
- Si se multiplican (o dividen) todas las observaciones de
una variable por la misma cantidad, la media de los
nuevos datos es la media de los datos originales
multiplicada (o dividida) por esa cantidad:
ax  ax
Ejemplo: Salarios
Supongamos que multiplicamos los salarios de los jefes
de ventas por 167 para expresarlos en pesetas:
167xi
34.500x167=5.761.500
5.126.900
5.494.300
6.012.000
5.694.700
5.644.600
5.427.500
7
 167 x
i
i1
7
 5594
. .500  167  33500
.
 167 x
5
- Si sumamos varias variables, la media de esa suma es
igual a la suma de las respectivas medias:
x  y ... z  x  y ... z
Ejemplo: Salarios
Además del salario anual de los jefes de ventas sabemos
también lo que cobran anualmente en especie (comidas,
coches, etc)
18.000
16.700
15.000
17.900
17.200
15.800
16.300
El salario en especie medio será:
7
y  y2  y3  y4  y5  y6  y7
y 1

7
y
i
i 1
7
 16.700
El salario total (metálico+especie) medio será:
x y
( x1  y1 ) ... ( x7  y7 )
 50.200  33500
.
 16.700  x  y
7
El salario medio en metálico es aproximadamente el
doble que el salario medio en especie.
6
La desviación típica
● La desviación típica es una medida de dispersión que
trata de medir la variabilidad de los datos alrededor de
la media.
● Veamos con un ejemplo por qué es importante:
Supongamos que tenemos los salarios en metálico de los
jefes de ventas de otra empresa:
34.000
27.500
31.600
39.700
35.300
33.800
31.700
- Su media es 33.500, la misma que los de la primera
empresa.
- Si nos basamos en la media no tendríamos elementos
para distinguir la distribución de salarios en las dos
empresas
¿Es la misma la distribución de los salarios en las dos
empresas?
7
NO, los de la segunda empresa están mucho más
dispersos (ver otro ejemplo en Figura 4.1 de Peña y
Romo)
● Una medida de posición, como la media, casi nunca es
suficiente por sí sola para resumir adecuadamente las
características de un conjunto de datos, necesitaremos
alguna medida de dispersión como la desviación típica.
● La desviación típica se define como:
N
Sx 
 x
i
 x
2
i 1
N
● Siempre toma valores positivos y mide la dispersión
alrededor de la media:
- Mayor Sx → mayor dispersión (ver Figura 4.2 de Peña y
Romo)
- En el caso extremo, si todos los datos fueran iguales,
 xi  x   0 y la desviación típica sería cero.
8
● El cuadrado de la desviación típica se llama varianza y se
representa por S x2
● La desviación típica también puede calcularse como:
N
Sx 
x
2
i
i 1
N
 x2
Ejemplo: Ejercicio 4.3 de Peña y Romo
Calcule la media y la desviación típica de los datos del
ejercicio 3.2 (nº de bibliotecarios en las bibliotecas públicas
españolas):
4 7 5 2 4 5 6 4 7 3 7 4 3 4 4 3 4 3 2 4 4 1 10 2 5 3 2 2 5 3 3 8
12 3 2 2 5 4 1 5 8 6 6 1 3 15 16 6 7 12
x
x1  x2 ... x50 4  7...12

 4,94
50
50
50
x
42  72 ...122  1759
.
Sx 
1759
.
 4,942  3,28
50
2
i
i 1
9
● Si transformamos una variable x en ax+b, la desviación
típica de la nueva variable será:
Sax b  a S x
donde a representa el valor absoluto de a, es decir a
siempre con signo positivo.
● Regla de Chebychev: Para cualquier conjunto de datos,
al
menos
el
1

100   1  2  por
 m 
ciento
de
las
observaciones están a una distancia de la media inferior
a m veces la desviación típica (ver Figura 4.3 de Peña y
Romo).
- Esta regla permite una interpretación de la desviación
típica como medida de concentración.
- Es una regla válida para cualquier conjunto de datos,
por lo que es bastante conservadora.
10
Ejemplo: GTINE: gasto total de 75 hogares
(pag. 15 Tema 2)
GTINE  x  275663
.
SGTINE  Sx  178.219
Si multiplicamos la variable GTINE por 5 tendremos:
5  GTINE  1378
. .315  5  275663
.
 5  GTINE
S5GTINE  891095
.
 5  178219
.
 5  SGTINE
Si a la variable GTINE le sumamos 2 tendremos:
2  GTINE  275665
.
 2  275663
.
 2  GTINE
S2GTINE  178219
.
 SGTINE
Si a la variable GTINE la multiplicamos por 5 y le
sumamos 2:
2  GTINE  5  1378
. .317  2  275663
.
 5  2  GTINE  5
S25GTINE  891095
.
 5  178219
.
 5  SGTINE
11
Según la regla de Chebychev el 75% de los datos
1

100   1  2  distan menos de 2 desviaciones típicas de la
 2 
media.
En el caso de GTINE están a menos de 2 desviaciones
típicas de la media 70 observaciones es decir el 93%.
12
El Coeficiente de Variación
● La desviación típica depende de las unidades de medida
y de la magnitud de los valores de la variable. Sin
embargo no es lo mismo una variabilidad de 100.000
pesetas si hablamos de la renta de los jóvenes que si
hablamos de la renta de un país.
● El Coeficiente de variación es una medida de dispersión
que no depende ni de las unidades de medida ni del
tamaño de los datos que se define como:
CVx 
Sx
x
Ejemplo:
Si comparamos las variables GTINE (gasto total de los
hogares) y G4 (gasto en menaje) tenemos:
GTINE  275.663
G4  19.880
SGTINE  178219
.
SG4  25505
.
CVGTINE 
178.219
 0,65
275.663
CVG 4  1,28
13
Ejercicio 4.10 (Peña y Romo)
Una empresa compra frutos secos en bolsas de 10 kilos y
los envasa y luego los vende en bolsas de 100 gramos. Se
dispone de datos reales en gramos del peso de 15 bolsas
de frutos secos de las que vende la empresa (las de 100
gramos) (X) y de datos reales en gramos del peso de 20
bolsas de las que compra la empresa (las de 10 kilos)
(Y).
a) Hallar la media y la desviación típica de cada uno de
los conjuntos de datos.
b) ¿Tiene sentido comparar las dos desviaciones típicas?
c) ¿Qué debe utilizarse para comparar la variabilidad de
ambos conjuntos de datos?
d) ¿Cuál de ellos tiene mayor variabilidad?
14
Xi2
9.604
11.236
7.744
8.281
8.836
8.649
9.025
7.921
9.409
7.569
8.649
9.216
7.056
9.801
8.100
Xi
98
106
88
91
94
93
95
89
97
87
93
96
84
99
90
15

X i 1400
.
15

X i2  131096
.
Yi
9.834
9.912
9.657
9.734
9.978
9.852
10.122
9.935
9.654
9.899
9.845
9.898
9.932
9.945
9.846
9.911
Yi2
96.707.556
98.247.744
93.257.649
94.750.756
99.560.484
97.061.904
102.454.884
98.704.225
93.199.716
97.990.201
96.924.025
97.970.404
98.644.624
98.903.025
96.943.716
98.227.921
9.952
9.923
9.934
9.834
99.042.304
98.465.929
98.684.356
96.707.556
i 1
i 1
20
 Y 197.597
i
i 1
15
X

20
Y
i
2
1952
. .448.979
i 1
20
Xi
i 1
N
1400
.

 93,33
15
Y
15
Y
i
i 1
N

197.597
 9.879,85
20
15
SX 

X i2
i 1
N
2
X 
131096
.
 93,332  5,41
15
20
SY 
Y
i
i 1
N
2
2
Y 
1952
. .448.979
 9.879,852  104,94
20
CVX 
SX
5,41

 0,058
X 93,33
CVY 
SY
104,94

 0,011
Y 9.879,85
Es menor la variabilidad de la variable Y
16
El Coeficiente de Asimetría
● El Coeficiente de Asimetría trata de medir la simetría de la
distribución alrededor de la media.
● El Coeficiente de Asimetría se define como:
N
CAx 
 x
i
 x
3
i 1
NS x3
Nótese que tiene en cuenta la distancia de cada
observación a la media (centro de simetría) conservando la
información sobre el signo de esa distancia.
● El Coeficiente de Asimetría no tiene unidades.
● El Coeficiente de Asimetría toma valor 0 cuando la
distribución es simétrica:
CA>0 → Asimétrica a la derecha
CA<0 → Asimétrica a la izquierda
Ver Figura 4.5 de Peña y Romo
17
El Coeficiente de Apuntamiento o kurtosis
● El Coeficiente de Apuntamiento trata de medir lo picuda o
plana que es la distribución.
● El Coeficiente de Apuntamiento se define como:
N
CApx 
 x
i
 x
4
i 1
NS x4
● Se suele dar su valor relativo respecto a una distribución
que se toma como referencia (generalmente la distribución
normal).
Ver Figura 4.6 de Peña y Romo
18
Descripción numérica de distribuciones de frecuencia
● En algunas ocasiones no conocemos los datos originales y
sólo tenemos la distribución de frecuencias.
● A partir de la distribución de frecuencias pueden definirse
cantidades análogas a las vistas hasta ahora que permitan
la descripción numérica de la distribución.
● Supongamos que queremos estudiar una distribución con
marcas de clase c1, c2, …, ck
y con frecuencias relativas
f1, f2, …, fk se pueden definir medidas análogas a las vistas:
k
Media: x c   ci f i
i 1
Desviación típica: Sc 
 c  x 
k
i
c
2
fi
i 1
k
Coeficiente de Asimetría: CAc 
 c  x 
i
3
c
fi
i 1
Sc3
k
Coeficiente de Apuntamiento: CApc 
19
 c  x 
i
c
i 1
Sc4
4
fi