Ejemplos tema 2 (Regresión y Correlación)
Anuncio
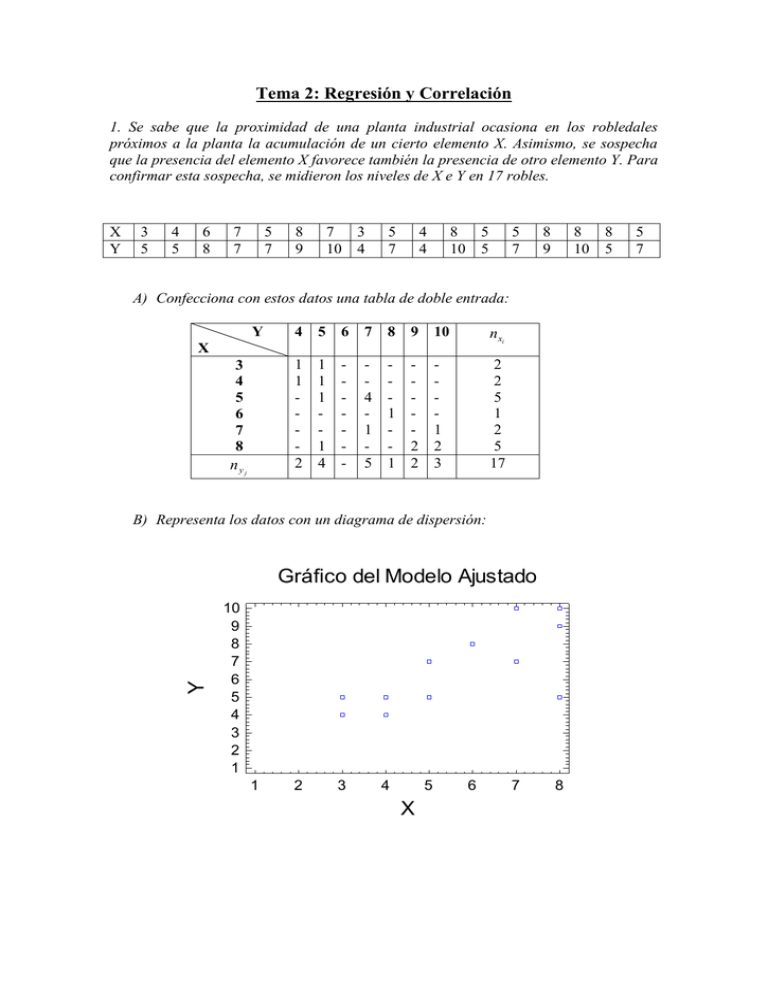
Tema 2: Regresión y Correlación 1. Se sabe que la proximidad de una planta industrial ocasiona en los robledales próximos a la planta la acumulación de un cierto elemento X. Asimismo, se sospecha que la presencia del elemento X favorece también la presencia de otro elemento Y. Para confirmar esta sospecha, se midieron los niveles de X e Y en 17 robles. 3 5 4 5 6 8 7 7 5 7 8 9 7 10 3 4 5 7 4 4 8 10 5 5 5 7 8 9 8 10 A) Confecciona con estos datos una tabla de doble entrada: Y 4 5 6 7 8 9 10 n xi 1 1 2 1 1 1 1 4 - 4 1 5 1 1 2 2 1 2 3 2 2 5 1 2 5 17 X 3 4 5 6 7 8 ny j B) Representa los datos con un diagrama de dispersión: Gráfico del Modelo Ajustado Y X Y 10 9 8 7 6 5 4 3 2 1 1 2 3 4 5 X 6 7 8 8 5 5 7 C) Calcula las medias, varianzas y desviaciones típicas marginales. xi 3 4 5 6 7 8 Total: nxi 2 2 5 1 2 5 17 xi.nxi 6 8 25 6 14 40 99 x2i.nxi 18 32 125 36 98 320 629 99 5,82 17 629 2 5,82 3,13 Varianza marginal de X: S X2 17 Desviación típica marginal de X: S X 3,13 1,768 Media marginal de X: x yj 4 5 6 7 8 9 10 Total: nyj 2 4 0 5 1 2 3 17 yj.nyj 8 20 0 35 8 18 30 119 y2j.nyj 32 100 0 245 64 162 300 903 119 7 17 903 7 2 4,11 Varianza marginal de Y: S Y2 17 Desviación típica marginal de Y: S X 4,11 2,027 Media marginal de Y: y D) Calcula la covarianza. S XY x y n i N j ij xy 3 4 1 3 5 1 5 7 4 8 10 2 5,82 7 739 5,82 7 2,7305 17 17 Para un cálculo más ordenado, se puede proceder del siguiente modo (especialmente útil cuando hay pocos datos, o las nij son casi todas iguales a 1): xi 3 4 6 7 5 8 7 3 5 4 8 5 5 8 8 8 5 Y entonces S XY yj 5 5 8 7 7 9 10 4 7 4 10 5 7 9 10 5 7 xi.yj 15 20 48 49 35 72 70 12 35 16 80 25 35 72 80 40 35 739 739 5,82 7 2,7305 17 2. Los manatíes son unos animales grandes y dóciles que viven a lo largo de la costa de Florida. Cada año las lanchas motoras hieren o matan a muchos de ellos. A continuación se presenta una tabla que contiene, para cada año, el número de licencias para motoras (expresado en miles de licencias) expedidas en Florida y el número de manatíes muertos en los años 1977 a 1990. Año 1977 1978 1979 1980 1981 1982 1983 1984 1985 1986 1987 1988 1989 1990 Licencias 447 460 481 498 513 512 526 559 585 614 645 675 711 719 Manatíes 13 21 24 16 24 20 15 34 33 33 39 43 50 47 a) Dibuja un diagrama de dispersión del número de manatíes muertos sobre el número de licencias anuales. ¿Qué indica el diagrama de dispersión? Gráfico del Modelo Ajustado Manaties 53 43 33 23 13 440 490 540 590 640 Licencias 690 740 b) Calcula el coeficiente de correlación lineal, e interpreta el resultado. Sumas: xi 447 460 481 498 513 512 526 559 585 614 645 675 711 719 7945 Marginales de x: x2i 199809 211600 231361 248004 263169 262144 276676 312481 342225 376996 416025 455625 505521 516961 4618597 yj 13 21 24 16 24 20 15 34 33 33 39 43 50 47 412 x y2j 169 441 576 256 576 400 225 1156 1089 1089 1521 1849 2500 2209 14056 7945 567 ,5 14 4618597 2 567 ,5 7843 ,5357 14 S x 88,56 S x2 Marginales de y: y 412 29,43 14 14056 2 29,43 137 ,87 14 S y 11,74 S y2 Covarianza: S xy 247521 567 ,5 29,43 978,546 14 Coeficiente de correlación: 978,546 0,94 88,56 11,74 Por lo tanto, la correlación lineal es muy fuerte, y positiva. xi.yj 5811 9660 11544 7968 12312 10240 7890 19006 19305 20262 25155 29025 35550 33793 247521 c) Halla la recta de regresión del número de manatíes muertos sobre el número de licencias anuales. y y y 29,43 S xy S x2 x x 978,546 x 567,5 y 0,1248x 41,37 7843,54 d) Si Florida decidiera congelar el número de licencias en 700.000, ¿cuántos manatíes resultarían muertos, aproximadamente, por las lanchas motoras? Sustituimos x 700 en la recta anterior, y obtenemos un valor aproximado de 46. e) Si nos dicen que un cierto año el número de manatíes muertos ha sido de 60, ¿qué número aproximado de licencias crees que habría, en ese instante? Indica hasta qué punto es fiable esta estimación. Necesitamos calcular la recta de regresión de x/y. xx S xy S y2 y y Sustituyendo los valores anteriores, se obtiene x 358,59 7,10y . En consecuencia, para un valor y 60 , obtendríamos un número aproximado de unas 785 licencias. 3. Las longitudes y pesos respectivos de cinco carpas del grupo de edad de tres años han sido: Longitud (cm): x Peso (gr): y 24 476 27 670 26 620 23 428 30 940 a) Ajusta los datos anteriores a una función potencial y axb b) Ajusta los datos anteriores a una función exponencial y abx , ó y ae x c) Halla, con cada una de las expresiones anteriores, el peso estimado para una carpa de ese grupo de edad con una longitud de 25 cm. a) Llamamos X=log x, Y=log y. xi 23 24 26 27 30 yi 428 476 620 670 940 Sumas: Xi=log xi 1,36172784 1,38021124 1,41497335 1,43136376 1,47712125 7,06539744 Yi=log yi 2,63144377 2,67760695 2,79239169 2,8260748 2,97312785 13,9006451 Xi2=(log xi)2 1,8543027 1,90498307 2,00214958 2,04880223 2,1818872 9,99212477 Yi2=(log yi)2 6,92449631 7,16957899 7,79745135 7,98669879 8,83948923 38,7177147 Xi.Yi=log xi.log yi 3,583310229 3,695663217 3,951159818 4,045141067 4,391670346 19,66694468 Recta de regresión de Y sobre X: Y 1,41728 2,9704X En consecuencia, log a 1,41728, b 2,9704. Por lo tanto, a 0,038 b 2,9704, es decir, y 0,038 x 2,9704 b) Llamamos X=x, Y=log y Sumas: xi=Xi 23 24 26 27 30 130 yi 428 476 620 670 940 Yi=log yi 2,63144377 2,67760695 2,79239169 2,8260748 2,97312785 13,9006451 Recta de regresión de Y sobre X: Y 1,50696 0,048968X Xi2 529 576 676 729 900 16900 Yi2=(log yi)2 6,92449631 7,16957899 7,79745135 7,98669879 8,83948923 38,7177147 Xi.Yi=xi.log yi 60,52320669 64,26256687 72,60218393 76,30401967 89,19383561 1807,083859 En consecuencia, log a 1,50696, logb 0,048968. Por lo tanto, a 32,13 , b 1,12 , y se tiene Y 32,13 1,12 x Si preferimos escribirlo en la forma y ae x , basta observar que e 1,12, de donde ln(1,12) (logaritmo neperiano). En consecuencia, 0,113, y el modelo es Y 32,13 e 0,113 x d) Sustituyendo x 25 en el modelo del apartado a), tenemos y 0,038 252,9704 539,79 Sustituyendo x 25 en el modelo del apartado b), tenemos 25 y 32,13 1,12 546,21