MEDIDAS DE POSICIÓN

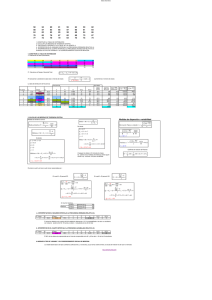
MEDIDAS DE POSICIÓN.
Las medidas de posición se usan para describir la posición que tiene un dato específico en
relación con el resto de los datos. Dos de estas medidas de posición más conocidas son los
cuartiles y los percentiles.
Cuartiles.
Son los valores de una variable que dividen en cuartos a los datos ordenados; Cada
conjunto de datos posee tres cuartiles. El primer cuartil, Q1, es el número tal que cuando
mucho el 25% de los datos es menor que el valor de Q1. El segundo cuartil es la mediana. El
tercer cuartil, Q3, es un número tal que cuando mucho el 75% de los datos es menor que Q3.
Esto se muestra en el siguiente esquema:
25%
25%
Min
Q1
25%
Q2
25%
Q3
Max
n
Percentiles.
Son los valores de una variable que dividen al conjunto de datos ordenados en 100
subconjuntos; cada conjunto de datos tiene 99 percentiles. El k-esimo percentil, Pk, es un
valor tal que cuando mucho (100-k) % de los datos es mayor. Esto se muestra en el siguiente
esquema:
1
%
Min
1
%
P1
1
%
P2
1
%
P3
P4
1
%
P5
1
%
P6
1
%
P7
Así hasta
P97
1
%
P98
1
%
P99
1
%
Max
Observaciones.
El primer cuartil y el 25avo percentil son iguales; es decir, Q1=P25. También, Q3=P75.
La mediana, el segundo cuartil Q2, y el 50avo percentil son iguales, Mediana = Q 2 = P50 , así
cuando se pida encontrar Q2 o P50, aplique el procedimiento para encontrar la mediana.
CUARTILES Y PERCENTILES PARA DATOS NO AGRUPADOS.
El procedimiento para determinar el valor de los cuartiles es el mismo que para los
percentiles y se muestran a continuación:
Paso 1. Ordenar los datos del menor al mayor.
nk
, donde n es el tamaño de la muestra y k la medida de posición
100
buscada (cuartil o percentil).
Paso 2. Calcular
Paso 3.
a) Si el resultado del cálculo anterior (
nk
) es un número entero, se le deberá sumar 0.5
100
nk
)
100
tomar como el siguiente entero más grande.
b) Si el resultado del cálculo anterior (
no es un número entero, este se deberá
Paso 4. Con la posición encontrada en el paso anterior, remitirse a los datos ordenados y
verificar a que valor de nuestros datos le corresponde la posición buscada.
Ejemplo resuelto.
Los siguientes datos corresponden al número de autos que llegan a diario al taller de la
empresa Dodge para su reparación, durante los meses de marzo y abril (40 días), de lunes a
viernes.
Determinar:
a) Primer cuartil Q1
b) Tercer cuartil Q3
c) El 45 percentil.
10
14
15
15
11
17
25
20
20
19
10
19
24
22
20
11
17
21
14
10
12
22
24
25
19
11
10
15
18
17
22
24
21
20
16
18
18
19
13
12
Paso 1. Ordenar los datos de menor a mayor.
10
12
17
19
22
10
13
17
19
22
10
14
17
20
22
10
14
18
20
24
11
15
18
20
24
11
15
18
20
24
11
15
19
21
25
12
16
19
21
25
Para el primer cuartil Q1.
Paso 2 .
n= 40 datos, k=25, ya que Q1= P25 (primer cuartil es igual al 25 percentil)
Q1=
nk
100
Q1=
40( 25) 1000
=
= 10
100
100
nk
= 10, el 10 es un número entero, por lo que se deberá de agregar 0.5,
100
entonces el Q1 se encuentra en la posición 10.5, entonces está entre 10 y 11avo dato.
Paso 3. Como
Paso 4. Q1 en este caso está entre 13 y 14 autos, Q1=
13 + 14 27
=
= 13.5
2
2
Q1=13.5 autos.
Para el tercer cuartil Q3.
Paso 2.
n= 40 datos, k=75, ya que Q3= P75 (tercer cuartil es igual al 75 percentil)
Q3=
nk
100
Q3=
40(75) 3000
=
= 30
100
100
nk
= 30, el 30 es un número entero se deberá de agregar 0.5, por lo que Q3
100
se encuentra en la posición 30.5
Paso 3. Como
Paso 4. Entonces Q3 está entre 30 y 31avo dato, Q3 está en este caso entre 20 y 21autos,
20 + 21 41
Q3=
=
= 20.5 Q3=20.5 autos.
2
2
Para el 45 percentil P45.
Paso 2.
n= 40 datos, k=45
P45=
nk
100
P45=
40( 45) 1800
=
= 18
100
100
nk
= 18, el 18 es un número entero se deberá de agregar 0.5, por lo que
100
P45 se encuentra en la posición 18.5, entonces está entre 18 y 19avo dato.
Paso 3. Como
Paso 4. P45 en este caso está entre 17 y 17 autos, P45=
17 + 17 34
=
= 17.5
2
2
P45=17.5 autos.
CUARTILES Y PERCENTILES PARA DATOS AGRUPADOS.
Si los datos se presentan en una tabla de distribución de frecuencia, los cuartiles y los
percentiles se determinan de la siguiente manera:
El primer cuartil es aquel que divide al 25% de los elementos del 75% de los valores
restantes, en una muestra o población y se calcula utilizando, la siguiente expresión:
n
− Fa
4
(Ac)
Q1 = L ri +
f
Donde: Q1=Primer cuartil.
Lri=Límite real inferior de la clase que contiene el primer cuartil.
n= Tamaño de muestra.
Fa= Número acumulado de las observaciones que preceden a la clase que contiene
el primer cuartil.
f = Frecuencia de la clase que contiene al primer cuartil.
Ac= Es el tamaño o amplitud de la clase donde se localiza el primer cuartil.
El tercer cuartil, es el valor que separa al 75% del 25% superior de los elementos de una
muestra y lo podemos obtener de la siguiente forma:
3n
− Fa
4
Q 3 = L ri +
(Ac)
f
Q3= Tercer cuartil.
Lri=Límite real inferior de la clase que contiene el tercer cuartil.
n= Tamaño de muestra.
Fa= Número acumulado de las observaciones que preceden a la clase que contiene
el tercer cuartil.
f = Frecuencia de la clase que contiene al tercer cuartil.
Ac= Es el tamaño o amplitud de la clase donde se localiza el tercer cuartil.
La amplitud cuartilica será = Q3 - Q1
De manera semejante, 99 percentiles dividen a una distribución en 100 partes iguales. La
amplitud percentilica es por lo general la distancia entre percentil 10 y el percentil 90.
Los percentiles se calculan de manera semejante a los cuartiles, Utilizando las siguientes
expresiones:
10n
− Fa
100
10°Percentil = L ri +
(Ac)
f
90n
− Fa
100
90°Percentil = L ri +
(Ac)
f
Ejemplo resuelto.
Si los datos del ejercicio anterior se presentan en una tabla de distribución de frecuencias,
hallar el primer cuartil (Q1), el tercer cuartil (Q3) y el 45 percentil (P45)
Tabla de distribución de frecuencias
Clase
N°
1
2
3
4
5
6
Límites de clase
Li
Ls
9
11
12
14
15
17
18
20
21
23
24
26
Límites reales de clase
Lri
Lrs
8.5
11.5
11.5
14.5
14.5
17.5
17.5
20.5
20.5
23.5
23.5
26.5
Frecuencia
Frecuencia relativa
fi
fri
7
0.175
5
0.125
7
0.175
11
0.275
5
0.125
5
0.125
40
marca de
clase
mi
10
13
16
19
22
25
frecuencia
frecuencia relativa
acumulada acumulada
fai
frai
7
0.175
12
0.3
19
0.475
30
0.75
35
0.875
40
1
Primer cuartil.
Como
n 40
=
= 10 en el decimo dato esta el primer cuartil, el cual corresponde a la clase 2.
4
4
n
− Fa
4
Q1 = L ri +
(Ac)
f
40
−7
Q1 = 11.5 + 4
(3)
5
10 − 7
(3)
5
9
Q1 = 11.5 +
5
Q1 = 11.5 + 1.8 = 13.3
Q1 = 11.5 +
Por lo tanto el cuartil Q1 es 13.3 autos.
Tercer cuartil (Q3).
3n 3(40) 120
=
=
= 30
4
4
4
clase 4.
Como
en el 30avo dato esta el tercer cuartil, el cual corresponde a la
3n
− Fa
4
Q 3 = L ri +
(Ac)
f
3(40)
− 19
4
Q 3 = 17.5 +
(3)
11
30 − 19
(3)
11
11
Q 3 = 17.5 + (3)
11
Q 3 = 17.5 + (3)
Q 3 = 17.5 +
Q3 es de 20.5 autos.
Percentil 45 P45
Como
45(40) 1800
=
= 18 , en el 18avo dato esta el P45, el cual corresponde a la clase a la
100
100
clase 3.
45n
− Fa
100
45°Percentil = L ri +
(Ac)
f
45(40)
− 12
100
45°Percentil = 14.5 +
(3)
7
45°Percentil = 14.5 +
18 − 12
(3)
7
6
45°Percentil = 14.5 + (3)
7
45°Percentil = 14.5 + 2.57 = 17.07
45° Percentil es de 17.07 autos.