distintos apartados

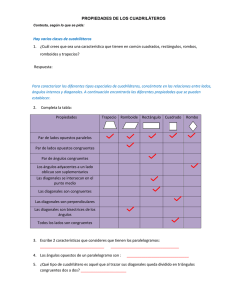
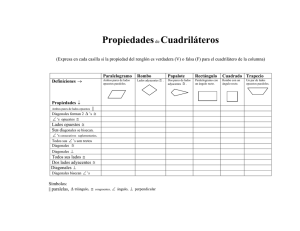
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 1
PÁGINA 232
REFLEXIONA
Para decidir el tipo de suelo que se pondrá en la Casa de la Cultura, hay
varios mosaicos.
Estos mosaicos tienen cinco tipos de losetas:
■ Todas estas losetas son cuadriláteros. Tres de ellas tienen los dos pares de
lados opuestos iguales. Identifícalas.
■ Comprueba que en ellas, y no en las otras, se cumplen las siguientes propiedades:
• Los ángulos opuestos son iguales.
• Los lados opuestos son paralelos.
• Las diagonales se cortan en sus puntos medios.
■ Las losetas 1-ª, 2-ª y 4-ª tienen los lados opuestos iguales. En ellas, los ángulos
opuestos son iguales, los lados opuestos paralelos y sus diagonales se cortan en
sus puntos medios. En las demás losetas (3-ª y 5-ª) no se cumplen ninguna de
estas propiedades.
PÁGINA 233
TE CONVIENE RECORDAR
1 Nombra cada uno de los siguientes polígonos:
a)
b)
d)
e)
a) Cuadrilátero
b) Pentágono
d) Hexágono
e) Heptágono
Unidad 12. Cuadriláteros
c)
c) Triángulo
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 2
2 Clasifica los siguientes cuadriláteros.
a)
b)
d)
e)
c)
a) Trapecio
b) Trapezoide
d) Rombo
e) Cuadrado
c) Rectángulo
PÁGINA 234
1 Di cuáles de las siguientes figuras son paralelogramos:
a)
b)
c)
d)
a) y d) son paralelogramos.
2 Construye un paralelogramo conociendo un lado, l3 cm, y las diagonales,
D8 cm y d6 cm.
Puesto que las diagonales se cortan en sus puntos medios, con las semidiagonales y el lado construimos un triángulo. Basándonos en él construimos todo el
paralelogramo.
3 cm
4 cm
4 cm
3 cm
3 cm
3 cm
Unidad 12. Cuadriláteros
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 3
3 Construye un paralelogramo sabiendo que todos sus lados miden 5 cm y
que dos de ellos forman un ángulo de 60°. ¿Cuánto miden los demás ángulos?
120°
5 cm
60°
120°
60°
5 cm
PÁGINA 235
1 Construye un rectángulo cuya diagonal mide 10 cm y uno de sus lados,
6 cm. Dibuja sus ejes de simetría.
A la mitad de su tamaño.
10 cm
10 cm
6 cm
6 cm
2 La diagonal de un rectángulo mide 10 cm y uno de sus lados, 6 cm. Halla el
otro lado.
El otro lado mide:
102 62 100
l 36
64
8 cm
PÁGINA 236
1 Construye un rombo cuyas diagonales midan 12 cm y 16 cm. Calcula la longitud del lado.
Unidad 12. Cuadriláteros
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 4
16 cm
12 cm
l
8
→ l 2 62 82 100 → l 10 cm
6
2 ¿Cómo se llama un paralelogramo que no tiene ningún eje de simetría?
Romboide.
3 Dibuja un rombo cuyos lados midan 5 cm y una diagonal, 8 cm. Calcula la
otra diagonal.
5 cm
8 cm
La otra diagonal mide:
d 2
d
52 42 9 → 9 3 → d6 cm
2
2
4 Dibuja un cuadrilátero con dos ejes de simetría que pasen, cada uno de ellos,
por dos vértices. ¿Cómo se llama?
Unidad 12. Cuadriláteros
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 5
Es un rombo.
PÁGINA 237
1 Construye un cuadrado de 6 cm de lado.
a) Traza sus ejes de simetría.
b) Calcula su diagonal.
6 cm
6 cm
La diagonal mide:
d 2 62 62 72 → d 72
8,5 cm
2 Construye un cuadrado cuya diagonal mida 8 cm. (Para hacerlo, recuerda
que las dos diagonales son iguales, perpendiculares y que se cortan en sus
puntos medios).
Unidad 12. Cuadriláteros
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 6
8 cm
8 cm
PÁGINA 238
1 De un trapecio isósceles conocemos sus bases, 26 cm y 36 cm, y sus lados
oblicuos, 13 cm. Halla la altura.
26 cm
a
5
36 cm
13 cm
a 2 132 52 144 → a12 cm de altura
5
2 Calcula el lado desconocido.
5 cm
6 cm
6 cm
x
8 cm
5 cm
x
x
x 2 52 22 21 → x 4,58 cm
2
8 cm
3 Construye un trapecio de lados 10 cm, 6 cm, 19 cm y 11 cm, sabiendo que el
primero y el tercero son paralelos.
Unidad 12. Cuadriláteros
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 7
Empezamos construyendo un triángulo de lados 6 cm, 11 cm y 19109 cm.
10 cm
11 cm
6 cm
9 cm
11 cm
10 cm
4 Dibuja un trapecio isósceles de bases 4 cm y 6 cm y cuyos lados iguales midan 3 cm. ¿Cómo son sus diagonales? Comprueba que tiene eje de simetría.
Empezamos construyendo un triángulo isósceles de lados 3 cm, 3 cm y
642 cm.
4 cm
3 cm
3 cm
2 cm
3 cm
Sus diagonales son iguales.
4 cm
PÁGINA 239
1 Dibuja en tu cuaderno un trapezoide de manera que tenga:
• Las diagonales iguales y perpendiculares.
• Los cuatro lados distintos.
Por ejemplo:
—
2 Dibuja
el cuadrilátero
ABCD
con las —
siguientes medidas: AB 6 cm,
—
—
—
BC 8 cm, CD 5 cm, DA 2 cm y AC 4 cm. ¿Qué peculiaridad tienen sus diagonales?
Con la diagonal, construimos los triángulos ABC y ADC:
Unidad 12. Cuadriláteros
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 8
B
A
C
D
Las diagonales no se cortan: una es interior y otra exterior.
PÁGINA 240
1 Halla las dimensiones de las figuras que se obtienen con los siguientes cortes
hechos a un cubo de 6 cm de arista, y represéntalas en tu cuaderno.
a)
6
3
El corte está hecho pasando por los puntos medios de
cuatro aristas.
3
3
b) 3
3
Observa que los cuatro lados son iguales. Halla su longitud.
c)
El corte contiene a dos aristas opuestas.
a)
32 32 18
a 4,2 cm
6 cm
a
Unidad 12. Cuadriláteros
Es un rectángulo de lados 6 cm y 4,2 cm.
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 9
b)
l
62 32 45
l 6,7 cm
Es un rombo de lado 6,7 cm.
c)
b
62 62 72
b 8,5 cm
Es un rectángulo de lados 6 cm y 8,5 cm.
6 cm
2 ¿Podrías obtener cuadriláteros cortando estas otras figuras? Di cómo.
a)
a)
Unidad 12. Cuadriláteros
b)
c)
Se producen cuadriláteros cortando el octaedro por cuatro de sus aristas.
12
SOLUCIONES A LAS ACTIVIDADES
DE CADA EPÍGRAFE
Pág. 10
b)
Cualquier corte perpendicular a las bases produce rectángulos.
c)
Realizando un corte que pase por las cuatro
caras, conseguimos un cuadrilátero.
Unidad 12. Cuadriláteros