Espectros de emisión y absorción. Los espectros de emisión y

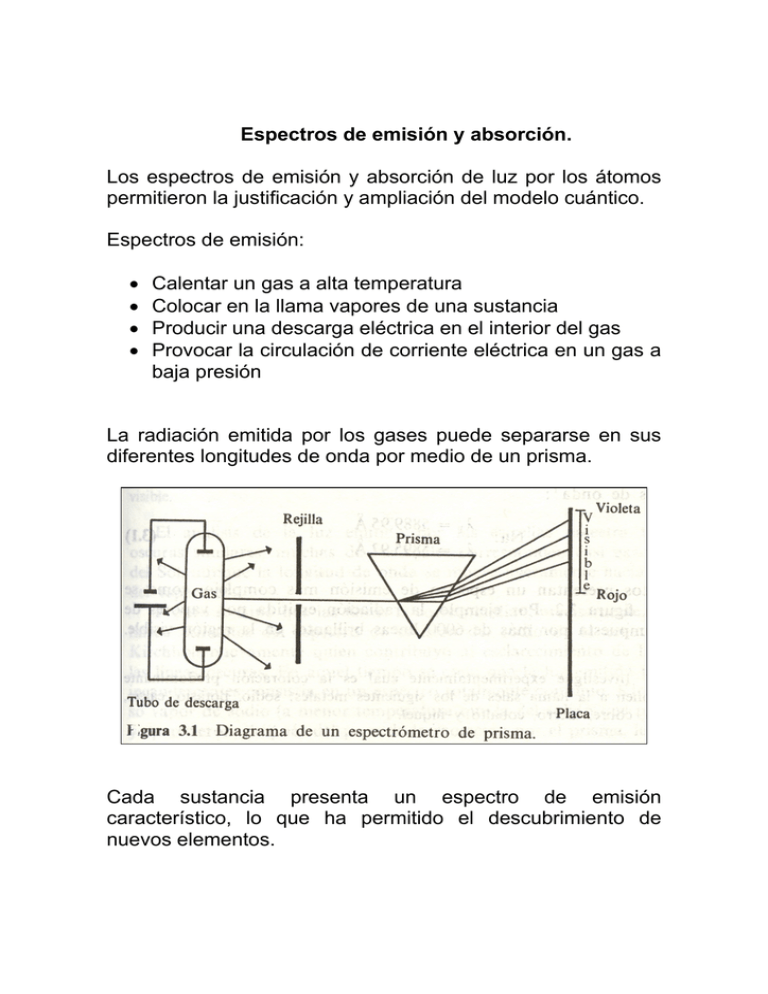
Espectros de emisión y absorción.
Los espectros de emisión y absorción de luz por los átomos
permitieron la justificación y ampliación del modelo cuántico.
Espectros de emisión:
•
•
•
•
Calentar un gas a alta temperatura
Colocar en la llama vapores de una sustancia
Producir una descarga eléctrica en el interior del gas
Provocar la circulación de corriente eléctrica en un gas a
baja presión
La radiación emitida por los gases puede separarse en sus
diferentes longitudes de onda por medio de un prisma.
Cada sustancia presenta un espectro de emisión
característico, lo que ha permitido el descubrimiento de
nuevos elementos.
Espectro de absorción
Wollaston en 1802 encontró siete líneas obscuras espaciadas
irregularmente. Doce años después Fraunhofer encontró
varios cientos de líneas oscuras.
Espectro de emisión del sodio
Espectro de absorción del sodio
La fórmula de Balmer
En 1885, Johann Jacob Balmer encontró una relación
numérica entre las líneas espectroscópicas. Estas coincidían
con los resultados experimentales reportados por Anders
Jonas Ångstrom.
⎛ n2 ⎞
λ = b⎜⎜ 2 2 ⎟⎟
⎝n −2 ⎠
Donde b=3645.6Å, para n= 3, 4, 5 y 6.
Problema:
Las líneas de emisión medidas por Ångstrom fueron:
Nombre de Hα
la línea
λ (Å)
6562.10
Color
Rojo
Hβ
Hγ
Hδ
4860.74
Verde
4340.1
Azul
4102.2
Violeta
Determina las previstas por la relación de Balmer así como el
porcentaje de error (⏐λ-λexp⏐/λexp)100
En 1890, Johannes Robert Rydberg encontró dos
generalizaciones fundamentales en los espectros de otros
elementos. Empleó números de onda:
ν =
1
λ
4⎛ 1 1 ⎞
− 2⎟
2
b⎝2 n ⎠
⎛1 1⎞
ν = RH ⎜ 2 − 2 ⎟
⎝2 n ⎠
ν= ⎜
RH=109677.581cm-1
Finalmente la ecuación correcta es:
⎛1 1⎞
ν = RH ⎜⎜ 2 − 2 ⎟⎟
⎝ n2 n1 ⎠
n1>n2
esta ecuación surge de aplicar la ecuación de Balmer
Con esta ecuación se reproducen las líneas de emisión del
Hidrógeno.
De modelos a modelos, el modelo del átomo.
Con el descubrimiento del núcleo atómico realizado por
Rutherford, se empezó a utilizar éste como base de un
modelo clásico del átomo.
Se consideraba la fuerza de atracción entre el núcleo y
electrón (para el átomo más sencillo) como la de Coulomb. La
representación era de un electrón atraído hacia una masa
mucho mayor que él. A este modelo se le denominó como
planetario.
Dado que el núcleo se encuentra en reposo y el electrón se
encuentra girando alrededor de él, la energía total sería:
1
Ec = mv2
2
V =κ
qq '
r
Ze2
V = −κ
r
1 2
Ze2
E = Ec + V = mv − κ
2
r
Considerar que la fuerza eléctrica es igual a Fe=m a
V
κZe2
E= =−
2
2r
La frecuencia, f, con la que gira el electrón dependerá del
radio de la orbita, r:
1 ⎛ κZe 2 ⎞
⎜⎜
⎟
f =
3 ⎟
2π ⎝ mr ⎠
1/ 2
Determinar las frecuencias y la energía para un átomo de
hidrógeno si r=1Å y r=2Å. Determinar la velocidad del
electrón.
Consideración clásica:
Como resultado de la emisión de radiación ultravioleta, la
energía del electrón se reduciría, lo que haría girar al electrón
más cerca del núcleo y a mayor velocidad. El átomo irradiaría
continuamente. Al acercarse más al núcleo, su energía
decrecería más y la radiación sería de mayor frecuencia.
De acuerdo con los resultados obtenidos, la trayectoria del
orbital sería una espiral y disiparía cada vez más energía
radiante de forma continua.
El modelo atómico de BOHR
En 1913, Niels Bohr desarrolló un modelo atómico
abandonando las consideraciones de la electrodinámica
clásica y tomando en cuenta la cuantización de la energía en
la interacción radiación-materia.
La propuesta de Bohr fue ponerle restricciones al modelo
planetario:
1. No se aplica el resultado clásico de que una carga
acelerada emite radiación continuamente.
2. El proceso de absorción y emisión de un átomo sólo
puede realizarse discontinuamente.
3. la cantidad de energía radiada en una emisión
fundamental debe ser igual a nhν
4. Cuando el átomo no absorba o emita radiación significa
que se encuentra en estado estacionario con una
energía constante.
5. La energía radiante tiene una sola frecuencia, la cual es
la mitad de la frecuencia a la que orbita el electrón en un
estado final (suponiendo que el electrón se acerca al
núcleo desde el infinito)
6. el núcleo es infinitamente más grande que el electrón.
− 2π 2κ 2 Z 2 e 4 m
E=
n2h2
n= 1, 2, 3,…
Determinar la energía
considerando n= 1, 2, 3
para
el
átomo
de
hidrógeno
A partir de estos resultados, Bohr propone órbitas
estacionarias, donde el valor de r para la primera órbita es
conocido como a0 o radio de Bohr.
o
h2
−11
a0 = 2 2 = 5.292x10 m = 52.92pm= 0.5292A
4π κe m
Así pues la expresión para la energía total puede expresarse
como:
⎛ 4π 2κe 2 m ⎞⎛ κZ 2 e 2
⎟⎟⎜⎜
E n = −⎜⎜
2
2
h
⎠⎝ 2n
⎝
En = −
Determinar la energía
considerando n= 1, 2, 3
⎞
⎟⎟
⎠
κZ 2 e 2 ⎛ 1 ⎞
⎜ ⎟
2a 0 ⎝ n 2 ⎠
para
el
átomo
de
hidrógeno
Para obtener la energía radiada cuando el átomo pasa de un
estado estacionario a otro propuso la siguiente relación:
2πκ 2mZ 2e4 ⎛ 1 1 ⎞
⎜⎜ 2 − 2 ⎟⎟
En = En 2 − En1 = −
2
h
⎝ n1 n2 ⎠
Er= -∆E
Considerando que la radiación es monocromática, tenemos:
2πκ 2mZ 2e4 ⎛ 1 1 ⎞
⎜⎜ 2 − 2 ⎟⎟
ν =−
3
ch
⎝ n2 n1 ⎠
Esta es igual a la propuesta por Rydberg para las líneas
espectrales del hidrógeno.
⎛1 1⎞
ν = − R∞ Z ⎜⎜ 2 − 2 ⎟⎟
⎝ n2 n1 ⎠
2
Donde R∞ es la constante de Rydberg.
Para determinar las transiciones entre las líneas espectrales:
En = E1 + hνnc
La teoría de Bohr justificaba la presencia de un menor
número de líneas.
En su estado más estable, el átomo puede absorber energía
para excitarse.
El estado inicial es n=1 y el final tendría una n de 2 en
adelante.
Al estado atómico con menor energía se le denomina estado
basal o fundamental. A cualquier otro se le denomina estado
excitado.
Los postulados de Bohr
1. Los átomos monoelectrónicos (H, He+, Li2+, Be3+,…)
están constituidos por un núcleo, de carga Ze, con una
masa M que es A veces mayor a la del electrón, el cual
gira alrededor del núcleo en una órbita circular de radio
r.
MH= 1836.1me
2. La cantidad de movimiento angular, L, del átomo está
cuantizada. De los infinitos movimientos orbitales
existentes de acuerdo al primer postulado, sólo son
posibles aquello para los cuales el momento angular sea
múltiplo entero de
h
=h
2π
Es decir L=n h
3. las órbitas determinadas por el segundo postulado son
estacionarias, es decir, el átomo no radía cuando se
encuentra en una de ellas. Sólo cuando el átomo cambia
de un estado (1) con mayor energía a otro (2) con menor
energía, se emite radiación monocromática cuya
frecuencia viene dada por
En1 − En2
ν=
h
⎡ 1
1 ⎤
ν = RH ⎢ 2 − 2 ⎥
n1 ⎦
⎣ n2
Las orbitas elípticas de Sommerfield
Las órbitas elípticas tienen energía negativa. Pero es
necesario considerar la distancia al núcleo, r, y al ángulo, φ
n
1
2
3
k
1
2
1
3
2
1
nr
0
0
1
0
1
2
b/a=k/n
1
1
½
1
2/3
1/3
Penetrabilidad:
Una orbita elíptica es más penetrante conforme más cerca
del núcleo puede pasar el electrón. A mayor excentricidad
de la elipse, menor valor de k, orbitas más penetrantes.
Localizabilidad:
Una orbita elíptica está más localizada conforme menos
varía la distancia al núcleo cuando el electrón gira. Las
orbitas menos excéntricas (k=n) son las más localizadas.
Si se considera el caso tridimensional, aparece un tercer
número cuántico. El número cuántico magnético, m.