Solución - Universidad Politécnica de Madrid

Dpto. O.E.I. – U.P.M.
ALGORÍTMICA
07/JUN/11
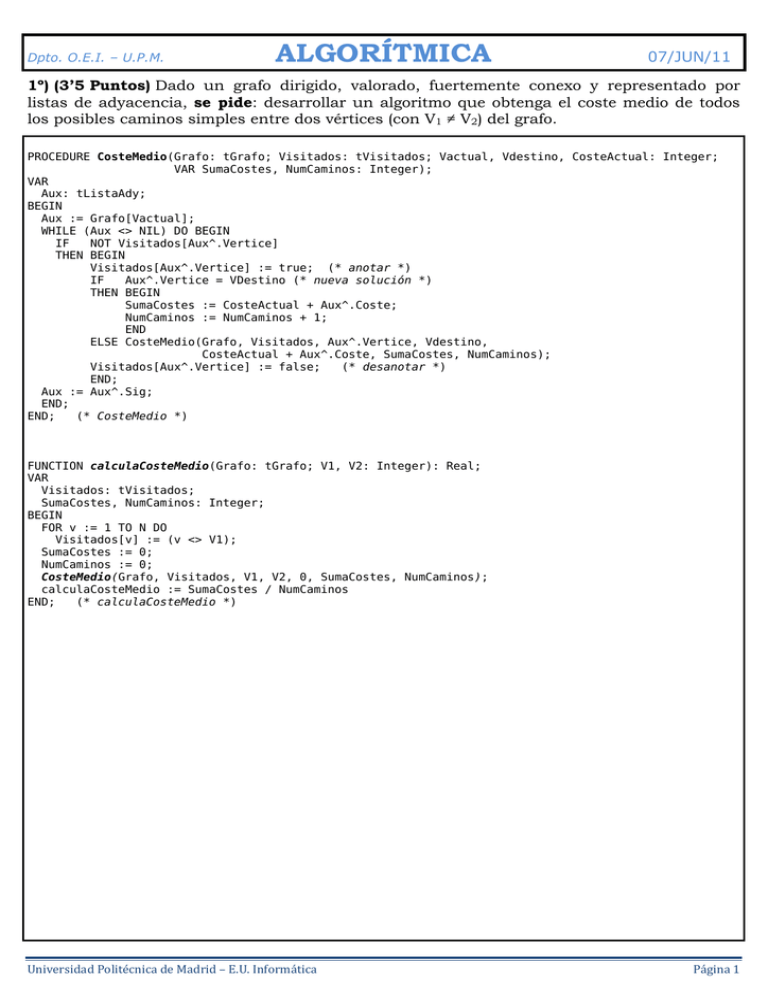
1º) (3’5 Puntos) Dado un grafo dirigido, valorado, fuertemente conexo y representado por
listas de adyacencia, se pide: desarrollar un algoritmo que obtenga el coste medio de todos
los posibles caminos simples entre dos vértices (con V1 ≠ V2) del grafo.
PROCEDURE CosteMedio(Grafo: tGrafo; Visitados: tVisitados; Vactual, Vdestino, CosteActual: Integer;
VAR SumaCostes, NumCaminos: Integer);
VAR
Aux: tListaAdy;
BEGIN
Aux := Grafo[Vactual];
WHILE (Aux <> NIL) DO BEGIN
IF
NOT Visitados[Aux^.Vertice]
THEN BEGIN
Visitados[Aux^.Vertice] := true; (* anotar *)
IF
Aux^.Vertice = VDestino (* nueva solución *)
THEN BEGIN
SumaCostes := CosteActual + Aux^.Coste;
NumCaminos := NumCaminos + 1;
END
ELSE CosteMedio(Grafo, Visitados, Aux^.Vertice, Vdestino,
CosteActual + Aux^.Coste, SumaCostes, NumCaminos);
Visitados[Aux^.Vertice] := false;
(* desanotar *)
END;
Aux := Aux^.Sig;
END;
END;
(* CosteMedio *)
FUNCTION calculaCosteMedio(Grafo: tGrafo; V1, V2: Integer): Real;
VAR
Visitados: tVisitados;
SumaCostes, NumCaminos: Integer;
BEGIN
FOR v := 1 TO N DO
Visitados[v] := (v <> V1);
SumaCostes := 0;
NumCaminos := 0;
CosteMedio(Grafo, Visitados, V1, V2, 0, SumaCostes, NumCaminos);
calculaCosteMedio := SumaCostes / NumCaminos
END;
(* calculaCosteMedio *)
Universidad Politécnica de Madrid – E.U. Informática
Página 1
2º) (3’5 Puntos) Se posee un tablero de ajedrez que contiene seis caballos blancos y el rey negro.
Inicialmente el rey se encuentra en la esquina inferior derecha y los caballos están dispersos en
posiciones conocidas del tablero. También se sabe que ningún caballo está en las esquinas del tablero.
Además, los caballos están fijos en el tablero y el rey se puede desplazar –siguiendo los movimientos
del rey de ajedrez- por cualquier posición que no esté amenazada por un caballo. El rey no puede
capturar ningún caballo.
Se pide: desarrollar un algoritmo que determine la longitud del camino más corto que debe seguir el
rey para llegar a la esquina superior izquierda. Si no existe camino se devolverá el valor infinito.
CONST
N = 8;
Movimientos = 8;
NCaballos = 6;
DestinoX = 1;
DestinoY = 1;
TYPE
TIndice = 1 .. N;
TTablero = ARRAY [TIndice, TIndice] OF Boolean;
TDesplazamiento = ARRAY [1 .. Movimientos] OF -2..2;
TCasilla = RECORD
X, Y: TIndice;
END;
TCaballos = ARRAY [1 .. NCaballos] OF TCasilla;
VAR
Tablero: TTablero;
DespReyX, DespReyY: TDesplazamiento;
DespCaballoX, DespCaballoY: TDesplazamiento;
Caballos: TCaballos;
MejorPaso: Integer;
PROCEDURE Inicializar_Desplazamiento(VAR DespReyX, DespReyY,
DespCaballoX, DespCaballoY: TDesplazamiento);
BEGIN
DespCaballoX[1] := -2;
DespCaballoY[1]:= 1;
DespCaballoX[2] := -1;
DespCaballoY[2]:= 2;
DespCaballoX[3] := 1;
DespCaballoY[3]:= 2;
DespCaballoX[4] := 2;
DespCaballoY[4]:= 1;
DespCaballoX[5] := 2;
DespCaballoY[5]:= -1;
DespCaballoX[6] := 1;
DespCaballoY[6]:= -2;
DespCaballoX[7] := -1;
DespCaballoY[7]:= -2;
DespCaballoX[8] := -2;
DespCaballoY[8]:= -1;
DespReyX[1] := -1;
DespReyY[1]
DespReyX[2] := -1;
DespReyY[2]
DespReyX[3] := -1;
DespReyY[3]
DespReyX[4] := 0;
DespReyY[4]
DespReyX[5] := 0;
DespReyY[5]
DespReyX[6] := 1;
DespReyY[6]
DespReyX[7] := 1;
DespReyY[7]
DespReyX[8] := 1;
DespReyY[8]
END; (* Inicializar_Desplazamiento
:= -1;
:= 0;
:= 1;
:= -1;
:= 1;
:= -1;
:= 0;
:= 1;
*)
PROCEDURE Inicializar_Caballos(VAR Caballos: TCaballos);
BEGIN
Caballos[1].X := 2; Caballos[1].Y := 2;
Caballos[2].X := 3; Caballos[2].Y := 4;
Caballos[3].X := 5; Caballos[3].Y := 5;
Caballos[4].X := 1; Caballos[4].Y := 5;
Caballos[5].X := 2; Caballos[5].Y := 7;
Caballos[6].X := 7; Caballos[6].Y := 7;
END; (* Inicializar_Caballos *)
Universidad Politécnica de Madrid – E.U. Informática
Página 2
PROCEDURE Inicializar_Tablero(VAR Tablero: TTablero; Caballos: TCaballos;
DespCaballoX, DespCaballoY: TDesplazamiento);
VAR
I, J, Nx, Ny: Integer;
BEGIN
FOR I := 1 TO N DO
FOR J := 1 TO N DO
Tablero[I, J] := False;
FOR I := 1 TO NCaballos DO
BEGIN
Tablero[Caballos[I].X, Caballos[I].Y] := True;
FOR J := 1 TO Movimientos DO
BEGIN
Nx := Caballos[I].X + DespCaballoX[J];
Ny := Caballos[I].Y + DespCaballoY[J];
IF (Nx IN [1 .. N]) AND (Ny IN [1 .. N]) THEN
Tablero[Nx, Ny] := True
END;
END;
END; (* Inicializar_Tablero *)
PROCEDURE Escribir_Tablero(VAR Tablero: TTablero);
VAR
I,J:TIndice;
BEGIN
FOR I:=1 TO N DO
BEGIN
FOR J:=1 TO N DO
IF Tablero[I, J] THEN
Write('1 ')
ELSE
Write('0 ');
Writeln;
END;
Writeln;
END; (* Escribir_Tablero *)
PROCEDURE Ensayar(Tablero: TTablero; X, Y: TIndice; Paso: Integer; VAR MejorPaso: Integer);
VAR
Posibilidad, Nx, Ny: Integer;
BEGIN
FOR Posibilidad := 1 TO N DO
BEGIN
Nx := X + DespReyX[Posibilidad];
Ny := Y + DespReyY[Posibilidad];
IF (Nx IN [1 .. N]) AND (Ny IN [1 .. N]) THEN
IF NOT Tablero[Nx, Ny] THEN
BEGIN
Tablero[Nx, Ny] := True;
IF (Nx = 1) AND (Ny = 1) THEN
MejorPaso := Paso
ELSE
IF Paso < MejorPaso THEN
Ensayar(Tablero, Nx, Ny, Paso + 1, MejorPaso);
Tablero[Nx, Ny] := False;
END
END;
END; (* Ensayar *)
BEGIN
Inicializar_Desplazamiento(DespReyX, DespReyY,
DespCaballoX, DespCaballoY);
Inicializar_Caballos(Caballos);
Inicializar_Tablero(Tablero, Caballos, DespCaballoX, DespCaballoY);
MejorPaso := MaxInt;
Ensayar(Tablero, N, N, 1, MejorPaso);
Escribir_Tablero(Tablero);
WriteLn('Numero de pasos = ',MejorPaso);
END.
Universidad Politécnica de Madrid – E.U. Informática
Página 3
3º) (3 Puntos) Dado un vector de tamaño N con números naturales ordenados
ascendentemente y sin repetidos, se pide: desarrollar en lenguaje Pascal un algoritmo que
determine si existe alguna posición en dicho vector en la que coincidan el índice y el
contenido del vector. En caso de existir, el algoritmo devolverá el índice de esa posición (-1 en
caso contrario).
NOTA: La complejidad de la solución desarrollada deberá ser logarítmica.
CONST
N = 5; (* Nº elementos del vector *)
Inicio = 15; (* índice inicio (un valor cualquiera) *)
Fin = Inicio + N - 1; (* índice fin *)
TYPE
tVector = ARRAY [Inicio..Fin] OF Integer;
VAR
Vector: tVector;
i: Integer;
FUNCTION BuscarCoincidencia(Vector: tVector; Iz, De: Integer): Integer;
VAR
Centro: Integer;
Encontrada: Boolean;
BEGIN
Encontrada := False;
WHILE NOT Encontrada AND (Iz <= De) DO (* búsqueda binaria *)
BEGIN
Centro := (Iz + De) DIV 2;
IF
Vector[Centro] < Centro
THEN Iz := Centro + 1
ELSE IF
Vector[Centro] > Centro
THEN De := Centro - 1
ELSE Encontrada := True
END;
IF
Encontrada
THEN BuscarCoincidencia := Centro
ELSE BuscarCoincidencia := -1
END;
(* BuscarCoincidencia *)
BEGIN
FOR i := 1 TO N DO (* Leer datos *)
BEGIN
Write('Introduce el elemento ', i, ': ');
ReadLn(Vector[Inicio + i - 1]);
END;
FOR i := Inicio TO (Inicio + N - 1) DO (* Mostrar datos *)
Write(Vector[i]:4);
WriteLn;
FOR i := Inicio TO (Inicio + N - 1) DO
Write(i:4);
WriteLn;
WriteLn('Coincidencia = ', BuscarCoincidencia(Vector, Inicio, Fin));
ReadLn;
END.
Universidad Politécnica de Madrid – E.U. Informática
Página 4