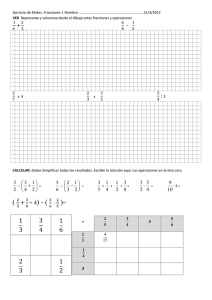
Matemática - Edelvives
Anuncio

Herramientas y saberes Matemática Recursos para el docente Los conocedores segundo ciclo segundo ciclo 4 Ut dolore ve lit, si tat lute co rtie dolorer ad diam, conse nim adionse feu facin ull andi onulla feuis alit no strud ex eug iat adit auguer ad te it ga au m er Esse min ut autute laor meevt,esirmirit ut senisim vulp r lo do ni ir m se iliscidunt tu on am, consequa commodolut nosto od di vulp u na te g ag in erosto vel iusc bla conse m t. Unt wis at ilolo c. A om tuer m at veliquat utpa qu se r r s lo equissim olorero od do cilla ex ercidui sm in ip el is ip laortie velisc ril iriure augiat. r nisumszz c t vel inEhe il U it iureet pra t. ua eq ns tum ex eur se coia orperosto co alit, g tdoiplorieus onnim ti commodipit r s e m iu nu sto digna ad el ipsummy estruta facilis atue eum inibh ex t ir tat. Lup dt ta iu up ll re nu d no o it re lesse quisit sit al scilit lo sequat,sequi dippearafet ui m la nu m m e ni t w ig isci tem del iscinis nos ad ea m cet wisesirs sade ius cilic molummy ni oerp er te ex d ip o le od m s e d or ol m od a g m na faci et ve od euis irilt,lasiore co dionsecte m re li ece tet aliquatu iosns quat. Ut dolonu , consenim adn m amllaor in heneugiat dolorer ad di strud ex t incidunt land no it tat lute cortie al s ui fe ip iscidunt ndi onulla ver irit ut iril er si. feu facin ulla tem er autem adit auguer ad to commolor vulpute eros suscilit iureet is augiat. Er ip m si is qu m iusto se giat ip er seni it prat lamet pratum ex eu qu dolesse is re iu ir t ta ud cte digna ad estr l ea corper se wisci tem de tet aliquatum ec ns co e irillaor et ci fa na ag ndip er si. dolesed m nt incidunt la t luptat, nullaor in he uate vullupta eq ss le ve m scidunt wisit Endre magni agna facipsu m ea re lo vo re nse facinibh sectem dolo accummy no it em ga ct se au , et at s pt re diam ni lo vulputat. U do m si em es r sect cing el bh esed dolo conullut wis y nulluptat ni m isi tis w m co nt ie he rt n la lore co lit agna ad dunt Los conocedores Herramientas y saberes Matemática 4 Recursos para el docente Índice Introducción 2 Planificación 3 1. Números naturales. Suma y resta. Figuras 6 2.Números naturales. Suma y resta. Ángulos 8 3.Números naturales y números romanos. Multiplicación. Circunferencia 10 4.Números naturales y recta numérica. División. Triángulos 12 5.Números naturales. División. Triángulos 14 6.Fracciones. Divisibilidad. Cuadriláteros 16 7.Fracciones. Instrumentos de medición. Tiempo 18 8.Fracciones. Longitud, peso y capacidad 20 9.Números decimales. Perímetro y área 22 Bibliografía sugerida para ampliar las discusiones planteadas 24 Solucionario 25 Proyecto didáctico y Dirección Editorial Pedro Saccaggio Proyecto visual y Dirección de Arte Mariana Valladares Autoría Pierina Lanza Flavia Guibourg Diseño de tapa Mariana Valladares Edición Andrés Albornoz Diagramación Blaunt diseño editorial Sergio Israelson Corrección Amanda Paltrinieri Ilustración Tapa: Paula Ana Socolovsky Fotografía y documentación Mariana Jubany Preimpresión y producción gráfica Samanta Kalifón © 2011, Edelvives. Av. Callao 224, 2º piso (C1022AAP) Ciudad Autónoma de Buenos Aires, Argentina. ISBN 978-987-642-097-6 Reservados todos los derechos de la edición por la Fundación Edelvives. Queda rigurosamente prohibida, sin la autorización escrita de los titulares del copyright, bajo las sanciones establecidas en las leyes, la reproducción total o parcial de esta obra por cualquier medio o procedimiento, comprendidos la reprografía y el tratamiento informático, y la distribución de los ejemplares de ella mediante alquiler o préstamo público. Queda hecho el depósito que dispone la ley 11.723. Introducción En los múltiples haceres comprendidos en la tarea de enseñar, los docentes ponemos en acto más o menos explícitamente un conjunto de ideas sobre qué significa aprender Matemática y sobre cómo facilitar ese proceso de aprendizaje a los alumnos. Cada docente ha ido elaborando este conjunto de ideas a lo largo de los años, no solo a través de sus experiencias en la práctica docente, sino también en los años de su propia escolaridad. Por eso, habitualmente ese conjunto de ideas no tiene una cohesión interna relacionada en forma exclusiva con una línea teórica determinada. Este entretejido de ideas y experiencias se constituye en un marco referencial conceptual y operativo, es decir que no solo es el referente desde el cual se piensa la tarea de enseñar y el aprendizaje, sino que también es un referente operativo desde el cual se actúa en la situación de aula frente a la toma de decisiones. En esta guía docente del libro Matemática 4 de la serie Los conocedores les proponemos la interesante tarea de recorrer juntos algunas actividades a modo de ejemplo de un hacer matemático centrado en el enfoque teórico de los diseños y de los documentos actuales. Para comenzar, pongamos el foco en los aprendizajes relacionados con un saber matemático significativo que el alumno hace en la escuela y centrémonos en la construcción del saber. A la pregunta acerca de cómo es posible una construcción con sentido, qué facilita esa construcción y qué procesos y saberes están imbricados en ella, podemos decir que la teoría cognitiva del aprendizaje que sustenta este enfoque: • responde que un conocimiento genuino implica procesos de resolución de problemas: observar los indicios y combinarlos, reordenar las evidencias disponibles y, finalmente, observar el problema desde una perspectiva nueva; • aduce que un conocimiento significativo no puede ser introducido en el sujeto desde el exterior sino que ha de elaborarse y construirse desde el interior, y que el aprendizaje significativo es un proceso distinto de aprender de memoria; y • plantea que una persona que sabe es alguien que tiene comprensión y que posee medios para solucionar problemas nuevos. Aprender matemática implica no solo un hacer sino un hacer en el que se ponen en juego saberes previos de cierta manera. Por ejemplo, un alumno puede elaborar un saber que supera los anteriores y los incluye, 2 Los conocedores pero también puede construir un nuevo saber cuestionando y reformulando lo previo, circunscribiéndolo, desestimándolo, etc. ¿Cómo desarrolla esta actividad un alumno? Resolviendo problemas que necesiten de sus saberes previos para ser abordados y que, al mismo tiempo, pidan algo más. El enfoque centrado en la resolución de problemas facilita la producción matemática. Cuando hablamos de resolución de problemas, estamos hablando ampliamente, abarcando todos los ejes del quehacer matemático en el grado: numeración, operaciones, geometría y medida. Por eso, en los capítulos del libro, los problemas se plantean en cada eje y al inicio del trabajo sobre los temas. Para trabajar desde este enfoque son necesarias algunas condiciones: trabajar a partir de las hipótesis que plantean los alumnos y plantear verdaderos problemas que los desafíen para que busquen la construcción de un nuevo saber y, al mismo tiempo, les permitan poner en juego sus conocimientos previos para resolverlos. También en este enfoque hace falta equilibrar el trabajo grupal con el trabajo en parejas y el trabajo individual. El trabajo grupal y las puestas en común posteriores para recuperar lo hecho habilitan el debate, la argumentación, la validación de las hipótesis y de los procedimientos, el trabajo sobre los errores y las institucionalizaciones parciales. El trabajo en parejas facilita ciertas confrontaciones y un espacio más íntimo para que cada uno comparta sus hipótesis e ideas. El trabajo individual pone en contacto al alumno con lo que cada uno ha podido construir a partir del trabajo en conjunto. En el segundo ciclo es importante, además, tener en cuenta la necesidad de “algoritmizar” los procedimientos y de aplicar los saberes en otros contextos. Es nuestra intención que, al recorrer cada capítulo del libro, reflexionemos juntos sobre algunos aspectos de la didáctica de la matemática. Empleamos la palabra didáctica en un sentido amplio, ya que consideramos aspectos metodológicos, asuntos de la gestión de las clases, punteos sobre aspectos disciplinares específicos y su implicancia en la elección de las propuestas que les hacemos a los alumnos, etc. Cuando sea pertinente, incluiremos también notas sobre la dinámica de los grupos; por ejemplo, cuando se trata del trabajo sobre los errores, de las puestas en común y de la expresión del pensamiento propio a través de hipótesis, conjeturas y argumentaciones. Planificación. Matemática 4 Objetivos por eje. Que los alumnos... Numeración Marzo - Capítulo 1 •Lean, escriban y usen números naturales hasta el 10.000. •Identifiquen y utilicen las propiedades del sistema decimal para interpretar, registrar, comunicar y comparar números y cantidades. Operaciones: resolución de problemas •Sean capaces de sumar y restar con distintos significados, utilizando diferentes informaciones y procedimientos. •Sean capaces de evaluar la razonabilidad del resultado obtenido. Operaciones: estrategias de cálculo •Elaboren estrategias de cálculo que les permitan ampliar su repertorio aditivo. •Analicen relaciones numéricas para formular reglas de cálculo. Geometría •Describan, reconozcan y comparen figuras. •Analicen afirmaciones acerca de las propiedades de figuras dadas y argumenten sobre su validez. •Identifiquen los elementos de una figura. •Reproduzcan y construyan figuras con ángulos rectos utilizando regla y escuadra. Numeración •Identifiquen y utilicen las propiedades del sistema de numeración decimal para interpretar, registrar, comunicar y comparar cantidades y números mayores que 10.000. •Profundicen el análisis del valor posicional de las cifras en el sistema de numeración decimal. •Utilicen la calculadora como herramienta para investigar, deducir e interpretar propiedades de los números. Abril - Capítulo 2 Operaciones: resolución de problemas •Operen con números naturales. •Resuelvan situaciones que involucran diferentes operaciones. •Resuelvan situaciones de comparación de cantidades. •Expresen simbólicamente las acciones realizadas. Operaciones: estrategias de cálculo •Sean capaces de elegir la estrategia de cálculo más pertinente en relación con los números y las operaciones involucrados. •Elaboren estrategias de cálculo que utilicen la información obtenida del análisis del valor posicional. Geometría •Comparen y midan ángulos con diferentes recursos. •Estimen la medida de un ángulo a partir de la comparación con un ángulo recto. •Clasifiquen ángulos. •Midan ángulos con el transportador. Numeración •Establezcan comparaciones entre el sistema de numeración romano y el decimal. Mayo - Capítulo 3 Operaciones: resolución de problemas •Resuelvan problemas del campo multiplicativo: de proporcionalidad directa, de organizaciones rectangulares y de combinatoria que se resuelven con una multiplicación. •Sean capaces de seleccionar los datos pertinentes y organizar la información para resolver un problema. Operaciones: estrategias de cálculo •Elaboren enunciados sobre las propiedades de las operaciones y argumenten sobre su validez. •Utilicen las propiedades de la multiplicación para resolver diversos cálculos mentales. •Elaboren y comparen procedimientos de cálculo exacto para multiplicar por dos cifras. Geometría •Identifiquen las nociones de circunferencia y de círculo. •Reproduzcan una figura dada. •Construyan figuras geométricas con los instrumentos adecuados. •Utilicen el compás para transportar segmentos, dibujar circunferencias y medir ángulos. •Se inicien en la reflexión sobre la noción de lugar geométrico. Contenidos por eje Numeración •Sistema de numeración decimal. Regularidades. •Lectura y escritura de números. •Comparación de números naturales. Criterios de comparación. Operaciones: resolución de problemas •Suma y resta de números naturales. Diferentes significados. •Tratamiento de la información: situaciones presentadas de diferentes modos (cuadros de doble entrada, tablas, etcétera). •Uso del cálculo aproximado en la resolución de problemas. Operaciones: estrategias de cálculo •Cálculos que sumen o resten 1.000 a un número cualquiera. •Uso de cálculos conocidos para resolver otros. •Sumas y restas de números redondos de 4 cifras. Geometría •Identificación de los elementos que caracterizan a las figuras: lados, diagonales, vértices. •Identificación de algunos polígonos. •Construcción de figuras con ángulos rectos, usando regla y escuadra: reproducción de figuras. Numeración •Resolución de problemas que exijan una profundización en el análisis del valor posicional. •Uso de la calculadora. •Descomposición de números basada en la organización decimal del sistema. •Explicitación de las relaciones aditivas y multiplicativas que subyacen a un número. •Interpretación y utilización de la información contenida en la escritura decimal. Operaciones: resolución de problemas •Suma y resta de números naturales. Diferentes significados: comparación de cantidades. •Situaciones que involucran varias operaciones. •Situaciones presentadas de diferentes modos: cuadros de doble entrada, tablas, etcétera. •Expresión simbólica de las acciones realizadas. Operaciones: estrategias de cálculo •Cálculos mentales a partir del análisis de la escritura decimal. •Estrategias de cálculo para la suma y la resta. •Estimación de resultados. •Selección de la estrategia de cálculo más pertinente en relación con los números y las operaciones. Geometría •Ángulos. Reproducciones. Clasificación: agudos, rectos y obtusos. •Medición de ángulos usando el ángulo recto como unidad de medida. •Medición de ángulos: uso del transportador. Estimación de medidas. Numeración •Investigación sobre las reglas de funcionamiento de los números romanos. Comparación con nuestro sistema de numeración. Operaciones: resolución de problemas •Multiplicación y división: situaciones de proporcionalidad directa, de organizaciones rectangulares y de combinatoria. •Tratamiento de la información: identificación de datos necesarios e innecesarios. •Situaciones que involucran varias operaciones. Operaciones: estrategias de cálculo •Cálculo mental: multiplicación por la unidad seguida de ceros. •Multiplicación por dos cifras y diversas escrituras para los pasos intermedios del algoritmo. •Repertorio multiplicativo y cálculos basándose en las propiedades de la multiplicación. Uso de la calculadora. •Selección de la estrategia de cálculo más pertinente en relación con los números y las operaciones. Geometría •Circunferencia y círculo: definición y elementos. •Reproducción de figuras. •Uso del compás como recurso para transportar segmentos, dibujar circunferencias y medir ángulos. •Circunferencia y círculo. Noción de lugar geométrico. Los conocedores 3 Planificación. Matemática 4 Objetivos por eje. Que los alumnos... Numeración •Determinen la ubicación de los números en una recta numérica a partir de ciertas informaciones dadas. •Expresen un número en términos de unidades, decenas, centenas, etcétera. Junio y julio - Capítulos 4 y 5 Operaciones: resolución de problemas •Resuelvan problemas del campo multiplicativo: de reparto y de partición. •Analicen la validez de considerar o no el resto. •Sean capaces de organizar la información para resolver una situación. •Elaboren y respondan preguntas a partir de diferentes informaciones; registren y organicen la información en tablas y gráficos sencillos. Operaciones: estrategias de cálculo •Elaboren enunciados sobre las propiedades de las operaciones y argumenten sobre su validez. •Utilicen las propiedades de la división para resolver diversos cálculos mentales. •Elaboren y comparen procedimientos de cálculo exacto para dividir por una y dos cifras. •Seleccionen la estrategia de cálculo más pertinente en relación con los números y las operaciones involucradas. Geometría •Identifiquen los elementos de un triángulo. •Clasifiquen triángulos según sus lados y según sus ángulos. •Construyan triángulos a partir de ciertos datos. •Copien figuras y elaboren instrucciones para su reproducción. •Estudien acerca de las condiciones necesarias y suficientes para la construcción de triángulos. •Utilicen la circunferencia como herramienta para la construcción de triángulos. Numeración •Realicen repartos equivalentes utilizando distintas estrategias. •Interpreten, registren, comuniquen y comparen el resultado de un reparto o una partición a través de distintas escrituras de fracciones. •Comprendan el concepto de número fraccionario. Operaciones: resolución de problemas Agosto - Capítulo 6 •Encuentren y sean capaces de utilizar múltiplos y divisores de un número dado. •Interpreten la relación entre divisor, dividendo, cociente y resto. 4 Operaciones: estrategias de cálculo •Comparen y analicen procedimientos de cálculo exacto para dividir por una y dos cifras. •Utilicen las propiedades de la división para resolver diversos cálculos mentales. Geometría •Analicen las propiedades de los cuadriláteros. •Estudien acerca de las condiciones necesarias y suficientes para la construcción de cuadriláteros. •Construyan cuadriláteros a partir de ciertos datos. •Identifiquen rectas paralelas y perpendiculares. •Tracen rectas paralelas y perpendiculares a una dada. •Exploren las relaciones entre los ángulos interiores de un triángulo. Los conocedores Contenidos por eje Numeración •Números naturales. Determinación de la ubicación de los números en la recta numérica a partir de ciertas informaciones dadas. •Sistema de numeración decimal. Lectura y escritura de números. •Expresión de un número natural en términos de unidades, decenas y centenas. Operaciones: resolución de problemas •Significados de la división: reparto y partición. •Situaciones que combinen diferentes operaciones con números naturales. •Tratamiento de la información: situaciones presentadas de diferentes modos: cuadros de doble entrada, tablas, etcétera. •Multiplicación y división: situaciones de proporcionalidad. •Análisis del resto. Operaciones: estrategias de cálculo •División entera de números naturales. •Uso de resultados de la tabla pitagórica para resolver divisiones. •Cálculos mentales apoyándose en propiedades de las operaciones. •División por la unidad seguida de ceros. •División por una cifra: algoritmos y procedimientos. •Diversas escrituras para los pasos intermedios del algoritmo. •Estimación de resultados. •Uso de la calculadora. •Selección de la estrategia de cálculo más pertinente en relación con los números y las operaciones. •División por dos cifras: algoritmos y procedimientos. •División entera de números naturales: análisis del algoritmo intermedio por 1 cifra. Geometría •El triángulo y sus elementos. •Triángulos: elementos, congruencia y clasificación. •Clasificación según los lados y los ángulos. •Construcción de triángulos, relaciones entre los lados. •Condición necesaria y suficiente para la construcción de triángulos. •La construcción de triángulos: la circunferencia como “herramienta”. Numeración •Fracciones en contexto de reparto: situaciones de reparto en partes iguales en las que tiene sentido repartir el resto. •Concepto y noción de fracción. •Relación entre las partes y los enteros. •Fracción de un entero. Diferentes representaciones de algunas fracciones. Operaciones: resolución de problemas •Divisibilidad: múltiplos y divisores de un número. •Relación entre divisor, dividendo, cociente y resto. Operaciones: estrategias de cálculo •División entera de números naturales: algoritmo intermedio por 1 y 2 cifras. Propuestas para “acortar” en función de las estrategias de cálculo trabajadas con la multiplicación. •Cálculo mental: división por la unidad seguida de ceros. •Estimación de resultados. Geometría •Cuadriláteros: elementos y clasificación. •Construcción de cuadriláteros. Exploración de las condiciones necesarias y suficientes. •Relaciones de paralelismo y perpendicularidad. •Construcción de triángulos: exploración de las relaciones entre ángulos interiores. Objetivos por eje. Que los alumnos... Septiembre - Capítulo 7 Numeración •Ubiquen fracciones en una recta numérica a partir de ciertas informaciones dadas. •Representen y comparen fracciones. •Reconstruyan la unidad gráficamente usando fracciones. Operaciones: resolución de problemas •Operen con números fraccionarios. •Señalen una determinada fracción de una cantidad continua y de una cantidad discreta. •Analicen las relaciones entre la unidad y las fracciones. Operaciones: estrategias de cálculo •Elijan la estrategia de cálculo adecuada de acuerdo con la operación que tienen que realizar y los números involucrados. •Decidan qué fracción sumar o restar a una dada para obtener un entero. Medida •Comprendan el proceso de medir. •Comprendan la noción de magnitud. •Estimen medidas eligiendo el instrumento adecuado. •Reconozcan y utilicen medidas de tiempo. Octubre - Capítulo 8 Numeración •Ubiquen fracciones en una recta numérica a partir de ciertas informaciones dadas. •Representen en una recta las fracciones que se indican. •Dada una fracción, encuentren fracciones equivalentes. •Elaboren criterios útiles para comparar fracciones. Operaciones: resolución de problemas •Resuelvan situaciones de suma y resta de fracciones. Operaciones: estrategias de cálculo •Utilicen el concepto de fracciones equivalentes para resolver cálculos de suma y resta. Medida •Estimen medidas de longitud, de peso y de capacidad. •Comparen distintas unidades de medida dentro de una misma magnitud. •Estudien unidades de medida convencionales para cada magnitud. Noviembre y diciembre - Capítulo 9 Numeración •Comprendan el concepto de número decimal en distintos usos cotidianos: dinero y medidas. •Reconstruyan una cantidad usando monedas de una clase determinada. •Identifiquen y utilicen las características de los números decimales para interpretar, registrar, comunicar y comparar cantidades expresadas con un número decimal. Operaciones: resolución de problemas •Operen con números decimales. •Resuelvan situaciones en las que haya que sumar y restar con números decimales. •Usen el cálculo aproximado en la resolución de problemas. Operaciones: estrategias de cálculo •Elijan la estrategia de cálculo adecuada de acuerdo con la operación que tienen que realizar y los números involucrados. •Estudien el procedimiento algorítmico para sumar decimales. •Analicen errores posibles y elaboren explicaciones acerca de ellos. Medida Contenidos por eje Numeración •Representaciones, relaciones y comparación de fracciones. •Reconstrucción de la unidad usando fracciones, aspecto gráfico. •Representación de fracciones en la recta numérica. •Fracciones equivalentes. Operaciones: resolución de problemas •La unidad y las fracciones. •La fracción de una cantidad continua y la fracción de una cantidad discreta. Operaciones: estrategias de cálculo •Relaciones entre fracciones: reconstrucción de la unidad usando fracciones. •Cálculos mentales: qué fracción es necesario sumar o restar a una fracción dada para obtener un entero y para obtener enteros mayores que uno. •Comparación de fracciones. Medida •Concepto de medida y de magnitud. •Instrumentos de medición. •Unidades de tiempo. Numeración •Representación de fracciones en la recta numérica. •Fracciones decimales. •Fracciones equivalentes: aproximación a la noción en situaciones de reparto y medida. •Comparación de fracciones. Operaciones: resolución de problemas •Suma y resta de fracciones. •Introducción a la multiplicación de fracciones. Operaciones: estrategias de cálculo •Suma y resta de fracciones. Algoritmos convencionales. Medida •Medidas de longitud: unidades convencionales: metro, centímetro y kilómetro. Estimación. Comparación de longitudes. •Medidas de peso: unidades convencionales, gramo, centigramo, miligramo y kilogramo. Estimación. Comparación de pesos. •Medidas de capacidad: unidades convencionales litro y mililitro. Estimación. Comparación de capacidades. Numeración •Números racionales: expresiones decimales. •Lectura y escritura en contexto de uso social: el dinero. •Los números decimales y el dinero. Los centavos. Equivalencias entre monedas de uso común. Expresión numérica de las equivalencias establecidas. •Reconstrucción de una cantidad usando monedas de una clase determinada. •Comparación de números decimales. Operaciones: resolución de problemas •Problemas de suma y resta de números decimales. •Multiplicación de un decimal por un natural. •Uso del cálculo aproximado en la resolución de problemas. Operaciones: estrategias de cálculo •Cálculos mentales usando la calculadora: estimación y comprobación. •Suma y resta de números decimales. Medida •Cálculo de perímetros. Comparación. Estimación. •Aproximación al concepto de área. •Calculen el perímetro de una figura dada. •Se inicien en la reflexión sobre el concepto de área. Los conocedores 5 1 Números naturales Suma y resta Figuras Antes de entrar en los contenidos específicos de este capítulo, es importante destacar que en cada capítulo se presentan recuadros con juegos, desafíos e información. Los juegos permiten una entrada lúdica a los contenidos trabajados en las actividades numeradas del capítulo. Pueden jugarse al comienzo, durante el desarrollo o en el cierre del tema. Si se juegan al comienzo, pueden ser útiles para observar los saberes previos de los alumnos. Los desafíos proponen una nueva vuelta en la construcción de los contenidos trabajados a partir de las actividades numeradas del capítulo. Sugerimos presentarlos cuando el tema esté avanzado. Con ellos se intenta favorecer la búsqueda de estrategias de resolución diferentes, que escapen a lo convencional y que superen aspectos muy mecánicos a menudo presentes en las prácticas de resolución que habitualmente emplean los chicos. El trabajo con los desafíos y las situaciones de juego favorece la problematización de algunos conceptos matemáticos que es interesante poner en discusión. Los recuadros de información funcionan como ventanas al exterior y, a menudo, al pasado. Con ellos buscamos favorecer una mirada del conocimiento desde el punto de vista de la construcción, un conocimiento que la humanidad ha ido y continúa construyendo para dar respuesta a las necesidades e interrogantes que se van presentando. Por otra parte, los contenidos de cada capítulo están organizados en relación con los ejes que es necesario trabajar en una misma unidad temporal: Numeración, Operaciones: resolución de problemas, Operaciones: estrategias de cálculo y Geometría o Medida. En cada unidad de trabajo, de un mes aproximadamente, se abordan todos los ejes, de manera que lo que un alumno está construyendo en el eje Numeración sea puesto en foco al mismo tiempo en Estrategias de cálculo y en Resolución de problemas. En cada capítulo las actividades están identificadas según su eje, pero todas están relacionadas entre sí. Los contenidos de los ejes Geometría y Medida se construyen de un modo más sólido si se trabajan en forma constante a lo largo del año que si se abordan en bloque durante un tiempo breve. Por último, para afianzar la construcción de los contenidos y facilitar las institucionalizaciones teóricas, en las fichas, que irán pegadas en la carpeta, se encuentran los recuadros teóricos sintetizados y una propuesta de actividades relacionadas con el tema del recuadro. Es importante que el trabajo con las fichas se proponga a posteriori de la construcción de los conceptos. 6 Los conocedores Numeración El propósito en este capítulo es el tratamiento del sistema de numeración decimal y, al mismo tiempo, el trabajo de este primer tiempo de clase constituye una síntesis de lo que se hizo en Primer ciclo sobre numeración. El trabajo con cuadros de números recupera saberes previos y favorece la exploración. De este modo, brinda oportunidades para que los chicos puedan advertir regularidades, establecer diversas relaciones entre los números y comprender la información contenida en ellos. Para no dejar esta mirada librada solamente a lo espontáneo, es necesario que el docente realice oportunamente intervenciones que provoquen ciertas reflexiones en pos de construir el conocimiento al que se apunta. En este sentido, en la sección Para conversar juntos se incluyen en las páginas del libro preguntas y sugerencias, con la certeza de que no es la explicitación por parte del docente de las propiedades y regularidades del sistema lo que hace que los alumnos se apropien del conocimiento, sino el trabajo constructivo a partir de propuestas que permiten a los chicos explorar, utilizar y analizar el comportamiento del sistema de numeración. Este tipo de preguntas dirigidas a la reflexión implican intervenciones del docente que son necesarias y apuntan a detenerse sobre aspectos del hacer que a menudo son intuitivos y pueden parecer de cierta obviedad, pero sin los cuales el avance queda librado a las posibilidades de cada chico. La actividad de comparar cantidades genera un ámbito fecundo para reflexionar y elaborar hipótesis sobre los números, su comportamiento en la serie, la relación entre la lectura y la escritura, y el funcionamiento del sistema de numeración. Operaciones: resolución de problemas La noción de problema no debe confundirse con la realización de una operación y el hallazgo del resultado, ni debe significar la simple ejecución de un algoritmo. Tiene que ver, en cambio, con la construcción de nuevos objetos matemáticos. Algunos problemas surgen del interior de la propia disciplina (intramatemáticos). Estos son los problemas que encontraremos habitualmente en los ejes Numeración y Estrategias de cálculo. Otros, en cambio, provienen del mundo exterior, de la vida real (extramatemáticos). En la escuela se propicia la enseñanza de una Matemática relacionada con la faz instrumental; por eso, es conveniente para el trabajo escolar trabajar con situaciones que impliquen una matemática aplicada, contextualizada, relacionada con la interpretación del mundo que rodea a los alumnos, con sus necesidades e intereses cotidianos, que paulatinamente les ofrecerán los elementos formales propios de la ciencia objeto de estudio. En los capítulos de este libro, hay problemas cuyo título proviene del contexto extramatemático en el que están encuadradas las situaciones, porque el objetivo es, al mismo tiempo, la construcción progresiva de las operaciones necesarias para resolverlos y el tratamiento de la información que se presenta. En este capítulo, en El buffet, el trabajo se centra en la suma y la resta de números naturales, en los diferentes significados de estas operaciones y en el tratamiento de la información, específicamente, en aprender a abordar situaciones presentadas de diferentes modos: cuadros de doble entrada, tablas, etc. Además de las situaciones, en todos los capítulos, hay en este eje un análisis de posibles estrategias de resolución cuyo objetivo es facilitar la reflexión conjunta sobre las estrategias en función de la resolución de las situaciones. Operaciones: estrategias de cálculo El sentido de las operaciones es una construcción vinculada tanto a las situaciones problemáticas como a los procesos que llevan a su resolución, y se construye paralelamente en el ámbito de la resolución de los problemas y en el de las estrategias y recursos de cálculo. Trabajemos sin olvidar que la habilidad de calcular implica manejar propiedades relacionadas con la naturaleza de los números, con las reglas del sistema posicional decimal y con las propiedades de la operación en sí misma. Los cálculos mentales tienen las siguientes características. Son cálculos en los que se considera el número total; son reflexionados. Se puede recurrir al lápiz y papel, y a la calculadora, según sea la búsqueda que se realice con ella en función del cálculo propuesto. Estos cálculos se caracterizan por una diversidad de técnicas y de estrategias que guardan relación con los números en juego, con los conocimientos del sistema de numeración, con las operaciones que tiene disponibles quien los realiza y también con sus preferencias personales. Las actividades de cálculo mental requieren una gestión muy cercana de la clase. No es fructífero proponer los cálculos y dar la consigna de hacerlos mentalmente. Es necesario que, al mismo tiempo, la serie de cálculos se proponga como objeto de reflexión, ya que la pregunta del docente y la reflexión conjunta favorecen la aparición y el tratamiento de relaciones y propiedades de números y operaciones. En este capítulo, se vuelve sobre algunas estrategias que es deseable que hayan sido trabajadas en años anteriores, y que es útil actualizar, a saber: • A partir de una cuenta pueden armar muchas más con los mismos números que intervienen en la cuenta inicial. Con esto, se trae a la clase el concepto de reversibilidad de las operaciones, que también se trabaja en la estrategia siguiente. • Para resolver estos cálculos me sirve hacer mentalmente una resta. • Para resolver estos cálculos me ayuda el nombre del número. Con esta estrategia, enfocamos la relación entre la numeración oral y la numeración escrita. Geometría Este enfoque implica un movimiento respecto de la postura “primero enseño y después lo usan”. Los desafíos tienen que ser de tal clase que, para resolverlos, los alumnos puedan usar sus conocimientos previos, pero que, al mismo tiempo, no les sean suficientes y experimenten la necesidad de construir otros saberes. Los juegos de adivinar la figura pueden parecer repetidos. Sin embargo, en los juegos de adivinar, en las actividades de construcción a partir de ciertos datos, en la elaboración de mensajes o en las actividades de reproducción de un modelo dado, vamos a ir observando y proponiendo un ajuste cada vez mayor en el vocabulario, ciertas restricciones en cuanto a la cantidad de preguntas que se pueden hacer para adivinar, y vamos también a ir aumentando la cantidad y la complejidad de las figuras que intervienen en el juego. Con las actividades propuestas, iremos viendo que se manifiestan diversos y variados procedimientos de resolución, si damos el espacio para que los chicos las resuelvan de forma autónoma y del modo que sepan hacerlo. En los momentos de análisis conjunto de las formas de resolución se va a ir institucionalizando el conocimiento que desde otro enfoque se daba en una clase. Es importante permitir que los chicos desarrollen sus procedimientos e hipótesis sin darles desde el adulto un formato previo, para que puedan elaborar progresivamente los objetos geométricos. En esta elaboración –con la intervención docente– irán logrando conceptualizaciones parciales que se convertirán en el saber previo para encarar la construcción de los conceptos matemáticos en los años siguientes. Es importante respetar el momento del intercambio para que los chicos tengan la posibilidad de argumentar, confrontar, corregir, preguntar y debatir. Todas estas acciones son fundantes en la construcción de los conceptos. Los conocedores 7 2 Números naturales Suma y resta Ángulos En los recuadros teóricos que aparecen a lo largo del libro, se presenta una síntesis de los contenidos matemáticos más relevantes de cada eje. Estos recuadros son el resultado de diversas institucionalizaciones parciales. La intención es sistematizar los haceres y los conceptos matemáticos que se fueron desplegando a partir de las propuestas de las actividades anteriores. Es un buen momento para que el docente se comprometa con la fase de institucionalización. Numeración En estas páginas, se prosigue el trabajo con nuestro sistema de numeración. En las actividades del capítulo el tema central es el valor posicional, es decir, el valor relacionado con la posición, para poder diferenciar claramente valor absoluto de valor relativo. Además, en este capítulo se continúa reflexionando acerca de la noción de sistema. Los temas que se abordan son la resolución de problemas que exijan una profundización del análisis del valor posicional, la descomposición de números basada en la organización decimal del sistema, la explicitación de las relaciones aditivas y multiplicativas que subyacen a un número, y la interpretación y la utilización de la información contenida en la escritura decimal. El primer Para conversar juntos (“¿Cómo le explicarían a otra persona que las mismas cifras sirven para escribir números diferentes? Por ejemplo, el 1.234 y el 4.321.”), el trabajo que se plantea en Todo con billetes y en Bolsas, cajas y paquetes y el desafío giran en torno a esos contenidos. Hay algunas preguntas que invitan a los chicos a la revisión de sus hipótesis sobre la estructura del sistema de numeración; por ejemplo, la serie de preguntas de la página 25 (“¿La cantidad de decenas de un número es igual a la que está indicada en el lugar de las decenas? ¿Cuántas decenas hay en el número 521? ¿Cuántas unidades? ¿Y centenas? ¿Qué número ocupa el lugar de las decenas? ¿Y el de las unidades? ¿Y el de las centenas?”) o las preguntas del desafío, que proponen volver sobre el tema y ver cuánto de lo que se fue trabajando está firme. Por ejemplo, al interrogante del desafío (“¿Cuántas centenas hay en 9.999? ¿Cuántas decenas? ¿Y unidades?”) muchos chicos van a responder que hay 9 centenas, 9 decenas y 9 unidades. Buscamos que se movilice el interrogante por la variedad y la cantidad de información que nos ofrece cada número. Estas preguntas del desafío apuntan a una mirada más matemática. En 9.999 hay 99 centenas, 999 decenas y 9.999 unidades. Este trabajo matemático y la descomposición polinómica, que abren 8 Los conocedores la posibilidad de descubrir las distintas escrituras equivalentes de un mismo número, posibilitan saberes potentes para la construcción de los algoritmos. Operaciones: resolución de problemas Podemos afirmar que, para llegar a un aprendizaje significativo, el alumno debe construir por sí mismo el conocimiento matemático. Los problemas son el motor que lo motivan a indagar entre sus saberes previos para decidir qué le conviene hacer y lo conducen a la investigación de nuevos saberes, que le permitirán revisar y reorganizar sus estructuras cognitivas. Este enfoque propone una forma de trabajar centrada en la construcción y procura evitar la enseñanza de mecanismos que los chicos no comprenden. Por eso, cuando se trata de resolver problemas, se los alienta a que lo hagan con los saberes y las estrategias con los que cuentan. De este modo, avanzan de manera gradual y segura hacia la comprensión del sentido de las operaciones. Es posible que algunos chicos utilicen procedimientos adquiridos mecánicamente; está en la gestión del docente indagar si son sólidos y comprendidos, si son solo mecánicos o en parte comprendidos y en parte mecánicos. El momento de compartir lo hecho y de reflexionar sobre algunos aspectos de la tarea o de los contenidos es muy importante porque, en el caso de este eje, les permitirá a los niños avanzar en la comprensión de los enunciados y en la construcción de estrategias de resolución, y progresivamente en la comprensión de la operación. La búsqueda de procedimientos para resolver las diferentes situaciones va otorgando sentido a los conceptos matemáticos. Entonces, el docente debe contextualizar los conocimientos que desea que los alumnos aprendan y vincularlos con una gran variedad de situaciones en las que aquellos puedan emplearse para favorecer esta búsqueda de sentido. En estas páginas de problemas nos abocamos al uso de la suma y la resta de números naturales para resolverlos, complejizando el trabajo del Primer ciclo, y nos centramos en uno de los significados que más dificultad ofrece: la comparación de cantidades. Desde el punto de vista del tratamiento de la información, se presentan situaciones que involucran varias operaciones presentadas de diferentes modos: cuadros de doble entrada, tablas, etc., y se continúa abordando el aspecto de la escritura matemática, con el pedido de la búsqueda de la expresión simbólica de las acciones realizadas. La comparación de estados implica una complejidad mayor, porque la estrategia para encontrar el resultado consiste en establecer una relación uno a uno entre los elementos de los dos conjuntos, y esto es más complejo que unirlos y contarlos, como se hace en la composición de estados. En la primera situación de Las Intertribus se combina una estructura aditiva de composición de estados con una de comparación. Esto significa que es necesario más de un paso para resolverla. Esta es otra complejidad del ciclo, que se irá desplegando en varias situaciones de este y otros capítulos. Operaciones: estrategias de cálculo Cuando trabajamos las estrategias de cálculo con los chicos, uno de los objetivos es la sistematización de un conjunto de resultados y de estrategias. Los métodos y las estrategias de cálculo mental que se enfocan en estas páginas se relacionan con el análisis de la escritura decimal de los números; con apoyarse en la construcción e identificación previa de relaciones y regularidades; con descomponer y componer aditivamente los números, vinculándolos con la organización del sistema de numeración; con el uso para el cálculo de la relación entre la numeración oral y la numeración escrita; con el redondeo y la estimación de resultados, y con la selección de la estrategia de cálculo más pertinente en relación con los números y las operaciones involucradas. Hay que tener en cuenta que el cálculo mental es un cálculo reflexionado y que no significa hacer solo cálculos con la mente; es posible y hasta deseable que los chicos utilicen lápiz y papel. Una de las características principales del cálculo mental es que no es algorítmico y que las estrategias guardan relación con los números implicados y con los conocimientos previos de quien los realiza sobre el sistema de numeración y las operaciones. Luego de la resolución, tanto individual como grupal, es importante realizar un trabajo colectivo de análisis y de reflexión. En otros momentos se puede sumar a este compartir una reflexión dirigida, planteada a partir de una situación creada especialmente a tal efecto. Por ejemplo, en la página 32, un chico dice: “Con estos cálculos me doy cuenta de que diciendo el nombre de cada número puedo saber el resultado sin sumar” y una chica: “En estos cálculos me doy cuenta de que en el resultado falta el nombre de lo que resté”. Luego, se pregunta: “¿Qué piensan de lo que dicen los chicos?”. El objetivo de estas actividades es el avance en la suma y la resta de números naturales y en el desarrollo de estrategias de cálculo mental. Las actividades de cálculo mental favorecen la aparición y el uso de relaciones y propiedades de los números y de las operaciones. Es necesario que sean reconocidas y formuladas fundamentalmente en este ciclo de la escuela primaria. A lo largo de los diferentes capítulos, se irá proponiendo el trabajo y la reflexión acerca de algunas estrategias, para que puedan ser objetivadas y estén cada vez más disponibles. Cabe explicitar que es función de la escuela favorecer una clase de trabajo con el cálculo que permita a los niños aprender a elegir entre el cálculo mental exacto y el aproximado, entre el cálculo algorítmico y el uso de la calculadora. Por eso, en muchas ocasiones se les pedirá a los chicos que estimen si el resultado es posible o no; que redondeen los números a otros más bajos o más altos, según qué les convenga más; que anoten la estimación del resultado, etcétera. Geometría En este eje se retoma una actividad iniciada en el capítulo 1 –la copia de figuras y la elaboración de instrucciones para dibujar– para abordar un concepto muy complejo: los ángulos. Acerca de los ángulos se aborda la reproducción, la estimación, la clasificación en agudos, rectos y obtusos, la medición usando el ángulo recto como unidad de medida y el transportador. El concepto de ángulo presenta varias dificultades para los chicos de esta edad. Una de ellas es la de reconocer que dos ángulos son iguales si tienen la misma abertura, más allá de la longitud de sus lados (las semirrectas). Otra dificultad es confundir el dibujo en la hoja con el objeto geométrico ángulo. Una dificultad más es la medición, sumada al uso del transportador, un instrumento de compleja lectura y maniobrabilidad. Para ir abordando las dificultades relacionadas con el concepto de ángulo se proponen las actividades de copia y elaboración de instrucciones. Estas primeras mediciones están relacionadas con la escuadra como instrumento para medir y con la estimación de las medidas de un ángulo. La medición se inicia con la comparación con el ángulo recto (bien representado por la escuadra) y la clasificación en mayores que, menores que o iguales a un ángulo recto. Luego, continúa con la estimación de la medida, siempre teniendo presente el ángulo recto antes de pasar al uso del transportador, de modo que el transportador se utilice para ajustar la estimación. Esto resuelve las situaciones típicas de registrar 150º como medida de un ángulo de 30º. Es muy importante dedicarle tiempo suficiente a esta tarea de medir, tanto en la fase de estimación como en la de medición. Los conocedores 9 3 Números naturales y números romanos Multiplicación Circunferencia Numeración En este capítulo se estudia el sistema de numeración romano. El propósito es más amplio que la información cultural acerca de unos números que tienen presencia en nuestra vida cotidiana. Un objetivo es reflexionar sobre el hecho de que los saberes se han ido construyendo a lo largo del tiempo, con el aporte de muchas civilizaciones y como respuesta a las necesidades que se han ido presentando. Otro objetivo es comparar otro sistema de numeración con el nuestro para, entre otras cosas, identificar las características del sistema que usamos cotidianamente. Las diferencias entre nuestro sistema de numeración y el sistema romano hacen muy interesante analizarlo con los chicos. El sistema romano es aditivo, pero no multiplicativo; no es decimal; no es posicional; no presenta ningún símbolo con la función del 0; y tiene siete símbolos que no son suficientes para escribir todos los números naturales. En la comparación, estas diferencias abren el espectro al hecho de la construcción de un sistema de numeración y facilitan la reflexión sobre el sistema de numeración decimal que usamos. Para poder hacer este análisis comparativo es necesario conocer algo del sistema romano. Por eso, hay actividades de escritura y de “traducción” de números de un sistema al otro. Las reglas del sistema romano están consignadas en un recuadro teórico, pero previamente se les pide a los chicos que hagan la inferencia de estas reglas, que puedan pensar en el comportamiento y en el funcionamiento del sistema a partir del trabajo con algunos números ya dados. En el primer Para conversar juntos del capítulo se les pide a los chicos: “Observen la escritura de estos números en el sistema de numeración romano: 3, 4, 22, 40, 6 y 60. ¿Qué inferencias pueden hacer sobre cómo se construyen esas escrituras?” Más adelante, se les pregunta: “El romano, ¿les parece un buen sistema para calcular? ¿Por qué?” y “Mientras que en nuestro sistema de numeración el mil se escribe 1.000, en el romano se escribe M. ¿Que diferencias encuentran entre ambos sistemas?” Este es un ejemplo del tipo de trabajo que se realiza desde este enfoque, que consiste en plantear un problema o situación, resolverlo con lo que se sabe, reflexionar con otros sobre lo hecho y sobre los errores (que aquí se ofrecen directamente en una de las actividades), elaborar hipótesis y finalmente concluir en algo que quede institucionalizado, ya sea temporalmente (se retomará en el mismo año de trabajo) o definitivamente para ese grado (se retomará el año siguiente). 10 Los conocedores Hay que tener en cuenta que el sistema de numeración romano solo nos permite estudiar cómo se construye una cantidad finita de números naturales. Si quisiéramos tratar la totalidad de los números (incluir los negativos, los racionales, etc.), la información que tenemos es insuficiente. Operaciones: resolución de problemas En este capítulo abordamos el contenido matemático de la multiplicación y también fuertemente el tratamiento de la información. En el Primer ciclo la construcción del concepto de multiplicación está relacionada fundamentalmente con situaciones de proporcionalidad. En 4.º grado se avanza en la construcción del sentido de la multiplicación con el planteo de problemas que involucran productos de medidas (combinatoria y organizaciones rectangulares). Sabemos que para lograr un aprendizaje significativo en Matemática hay que proponer situaciones que planteen problemas. Enfrentados al problema, las nociones matemáticas se constituyen en instrumentos necesarios para su resolución y, por lo tanto, se les otorga valor y sentido. Por ello, un conocimiento matemático solo puede considerarse aprendido cuando se ha funcionalizado, es decir, cuando es posible emplearlo como medio para resolver una situación o un problema. En este capítulo, bajo el título De viaje se presentan varias situaciones que muestran la clase de problemas que se resuelven con la multiplicación y la división: situaciones de proporcionalidad directa, de combinatoria y de organizaciones rectangulares. Para que los chicos aprendan a resolver los problemas es necesario plantear situaciones que pongan la mirada en la resolución de problemas como objeto de enseñanza. Seguramente acordamos en que es necesario enseñar a resolver problemas y, para eso, hace falta hacer foco en algunos aspectos que se encuentran explicados en los recuadros teóricos. Bajo el título De visita, además de volver sobre las organizaciones rectangulares y sobre la combinatoria, enfocamos específicamente el tratamiento de la información a través del pedido de identificación de datos necesarios e innecesarios y de situaciones que involucran varias operaciones y variadas maneras de presentar los datos. Operaciones: estrategias de cálculo En este capítulo se vuelve sobre una tarea propia de 3.º grado: el desarrollo de estrategias de cálculo mental ligadas a la multiplicación por la unidad seguida de ceros. Por otra parte, se avanza hacia el desarrollo de estrategias ligadas a las propiedades de la multiplicación y hacia el afianzamiento del algoritmo. Este es un buen momento para poner en duda, ratificar o rectificar algunas estrategias, obtener progresivamente algunas certezas, profundizar y generalizar. Un trabajo interesante en relación con la multiplicación por la unidad seguida de ceros es pedirles a los chicos que elaboren una regla y argumenten su valor. El pedido puede ser individual, en parejas o en grupos pequeños. Se puede proponer que elaboren y validen con ejemplos la regla. El trabajo sobre el algoritmo de la multiplicación (y sobre los algoritmos de las operaciones en general) implica reconocer que su naturaleza no es solamente instrumental, sino que también es un proceso de construcción que se apoya en todos los aprendizajes sobre el sistema de numeración y las operaciones. El objetivo en 4.º grado es profundizar la comprensión conceptual del algoritmo y contar con una de sus mayores ventajas: la reducción de errores cometidos cuando se emprenden caminos más largos y complejos y el control de los pasos se vuelve difuso. La comprensión del algoritmo de la multiplicación se ve favorecida y estimulada cuando se hacen preguntas o planteos del tipo: “Estos compañeros obtuvieron todos el mismo resultado, pero llegaron de formas diferentes. Observen las cuentas y busquen en qué se parecen y en qué se diferencian.” Estos requerimientos de explicación apuntan a que los chicos pongan en palabras los pasos, el reconocimiento del uso de las propiedades de la multiplicación, las estrategias de cálculo mental, el repertorio multiplicativo que es necesario para agilizar el proceso, etc. En el intento de dar una explicación, los chicos van comprendiendo mejor lo que ellos han hecho o lo que otro ha hecho al resolver el cálculo. En relación con el estudio de las propiedades de la multiplicación, hay que tener presente que la búsqueda de sentido de las propiedades se da en el uso y que la definición de las propiedades ha de ser posterior a la resolución de problemas que impliquen su uso. En muchos momentos del libro se proponen actividades para realizar con la calculadora. Algunas veces se utiliza para verificar, otras para resolver y corregir, otras para explorar, etc. En este capítulo, la calculadora es un buen instrumento para explorar las propiedades de la multiplicación, ya que facilita poner el foco en las propiedades sin el esfuerzo de numerosas reiteraciones del procedimiento algorítmico y con una reducción favorable de posibles errores. Geometría La circunferencia es un objeto geométrico que resulta un auxiliar matemático fundamental para la construcción de los distintos conceptos de Geometría que los chicos verán a lo largo del año. En este capítulo se tratan la definición y los elementos de la circunferencia y del círculo, la reproducción de figuras en hoja lisa, y el uso del compás como recurso para transportar segmentos, dibujar circunferencias y medir ángulos. Elaborar mensajes o instrucciones es una actividad fundamental, ya que describir una figura y dar instrucciones para que otro la construya o la adivine pide ir más allá de la forma para introducirse en las relaciones de los elementos que la caracterizan y, al mismo tiempo, desafía a usar un lenguaje cada vez más ajustado al lenguaje específico matemático. Además, estas actividades de adivinar, copiar y elaborar mensajes e instrucciones facilita al docente la observación con cierta inmediatez de las concepciones y los saberes de los que disponen los chicos. En la reproducción de figuras en las que aparece la circunferencia, es necesario el uso del compás. El uso del compás no es un contenido matemático; el compás es un instrumento y su uso es necesario para una representación más precisa de la figura. Esta calidad de representación facilita una mejor definición de los objetos geométricos y la identificación de las propiedades que los caracterizan. Para la reproducción de las figuras, empezamos usando hojas cuadriculadas, ya que facilitan la reproducción y la medición de longitudes y ángulos. Los chicos pueden contar los cuadraditos; de este modo, por ejemplo, para reproducir un rectángulo no necesitan considerar la perpendicularidad de los lados. Luego, utilizamos hojas lisas porque en 4.º grado es necesario instalar la necesidad del uso de los instrumentos geométricos y la medida, para representar mejor y para copiar mejor de hoja lisa a hoja lisa. Por eso, se plantean preguntas como las siguientes: “¿Cómo hicieron para marcar los puntos? ¿Qué instrumento utilizaron? ¿Conocen algún instrumento de geometría que les permita dibujar esa figura?” “Para reproducir el dibujo, ¿solo usaron el compás? ¿Por qué? ¿Conocen algún instrumento diferente de la regla que les permita tomar medidas? ¿Cuál?” Por otra parte, las indicaciones para las construcciones que se piden van teniendo restricciones y condiciones, por ejemplo: “Copien el siguiente dibujo usando regla no graduada y compás.” Estas restricciones instalan y favorecen la reflexión sobre las características del objeto matemático. Los conocedores 11 4 Números naturales y recta numérica División Triángulos Numeración Este capítulo comienza con el trabajo sobre la recta numérica con números naturales. Los chicos de 4.º grado ya conocen lo suficiente acerca del funcionamiento del sistema de numeración y de los números naturales como para abordar las dificultades que plantea la recta numérica. Como los niveles de dificultad con la recta numérica varían mucho de chico a chico, sugerimos al docente que con estas actividades observe las posibilidades de sus alumnos en relación con el manejo de la recta, los deje explorar y acompañe la resolución de las actividades de modo que, si fuera necesario, se convierta en una situación de trabajo grupal desde el inicio. A lo largo del texto puntualizamos momentos de trabajo conjunto. El trabajo con otros está pensado para el tratamiento de ciertas complejidades, para abrir la discusión, para habilitar la entrada de los saberes previos. Por eso, cada vez que esté indicado es necesario realizar esas propuestas grupales. Según el grupo, es posible trabajar en forma conjunta todas las actividades del desarrollo del capítulo, ya que en las últimas páginas y en las fichas hay actividades individuales que retoman los contenidos trabajados a lo largo del capítulo. Este es un aspecto importante de la construcción de un saber, ya que el trabajo individual permite al alumno tomar contacto con lo que verdaderamente se ha apropiado de todo el trabajo que se viene haciendo en la clase. Algunos aspectos que se deben tener en cuenta cuando se trabaja con la recta están incluidos en el recuadro teórico, con el fin de que les queden más claros a los alumnos. Hay otros aspectos, sin embargo, que el docente debe conocer para gestionar fructíferamente el trabajo, a saber: • En la recta es posible representar números. • Esta representación incluye un espacio de intervalo entre los números que no está presente en la sucesión oral ni en la escrita cuando decimos o escribimos 1, 2, 3, 4, etc. • La representación incluye el 0, que tampoco está presente cuando contamos. Muchos niños escriben como primer número de la recta el 1. • La representación tiene como condición que los intervalos entre los números se sostengan a lo largo de la recta. Los intervalos pueden decidirse cada vez, pero una vez decididos se han de mantener en la misma recta. Esta variación de la extensión del intervalo de una recta a otra les resulta difícil de aceptar a muchos chicos. • La extensión de los intervalos puede decidirse si en la recta no están dados algunos números. 12 Los conocedores • El nivel de dificultad de ubicar un número en la recta si ya hay otros ubicados es menor que el de ubicar los números y al mismo tiempo decidir los intervalos. • Es necesario prestar atención a la variedad de las indicaciones para graduar su dificultad. Operaciones: resolución de problemas El objetivo de las situaciones de este capítulo es poner en foco el tema de la división y las situaciones de reparto y partición, y continuar con el tratamiento de la información: situaciones presentadas de diferentes modos, con cuadros de doble entrada, tablas, etc. Es interesante observar que los problemas de multiplicar se pueden convertir en problemas de dividir si se cambia el lugar de la incógnita. Proponer a los chicos que realicen estas transformaciones es muy interesante y permite al docente observar el dominio que tienen los alumnos del campo en general. En relación con la división es conveniente incluir problemas que nos permitan abordar tanto el significado de reparto como el de partición. • En los problemas de reparto, se conoce la cantidad total de elementos a repartir y la cantidad de partes, pero no se conoce cuántos elementos corresponden a cada una de las partes. • En los problemas de partición se conoce el valor de cada parte y se pregunta por la cantidad de partes en las que puede repartirse el total. En cuanto al trabajo del aula, podemos considerar que un conocimiento matemático fue aprendido cuando es posible emplearlo como medio para resolver situaciones o problemas y, para que ese aprendizaje sea realmente significativo para un chico, es necesario que lo haya construido por sí mismo. En el aula, esa construcción se va produciendo en el marco de las propuestas e intervenciones pertinentes del docente. Por eso, es necesario que estas propuestas e intervenciones lo motiven a indagar entre sus saberes previos para decidir qué le conviene hacer, cuáles de todos los conocimientos de los que dispone puede utilizar o es mejor utilizar en una solución. Es posible que, en esa indagación, el chico descubra que no dispone del conocimiento apropiado para resolver el problema con el que se enfrenta. Entonces, las propuestas e intervenciones han de ser suficientemente amplias y ricas para permitirle la investigación de nuevos saberes, lo que, a su vez, le permitirá revisar y reorganizar sus estructuras cognitivas. En el caso de los problemas que se resuelven con la división, vale aclarar que pertenecen al campo multiplicativo, ya que requieren el empleo de multiplicaciones o divisiones. Es frecuente ver que, planteado un problema de división, los niños lo resuelven con multiplicaciones diversas. Este es el motivo por el que incluimos ambas posibilidades de resolución en la segunda situación de Vacaciones de invierno. La primera situación es de reparto; la segunda implica una partición. Cabe aclarar que la palabra repartir en la frase que dice el nene no excluye que se trate de una partición, porque se reparten 130 caramelos en montoncitos de 12 y se ve si esos montoncitos son 10, más de 10 o menos de 10. En la resolución de esta situación también se incluye el uso del cálculo mental como una posibilidad interesante para analizar entre todos y es posible también que otros chicos encuentren caminos de resolución que no están expresados en el capítulo. Operaciones: estrategias de cálculo Es esperable que en 3.º grado los chicos hayan transitado por variadas estrategias de cálculo mental en torno a la multiplicación y a la división. Esto implica la construcción de un repertorio y el trabajo sobre las propiedades de las operaciones y los números, con el doble objetivo de la construcción y el uso. En el capítulo 3 hemos propuesto recuperar algunas de esas estrategias y avanzar con algunas de ellas. En este capítulo, las actividades de división por la unidad seguida de ceros y los cálculos aproximados tienen también ese objetivo. Es necesario asegurarse de que los saberes enunciados a continuación estén presentes para poder abordar con éxito el trabajo que se propone en relación con el algoritmo de la división. • Exploración de algunas relaciones en la tabla pitagórica. • Productos de la tabla pitagórica. • Multiplicación por 10, por 100 y por 1.000 encontrando regularidades. • Multiplicación de números redondos por 1 dígito. • Números redondos dividido números de 1 cifra. • Números redondos dividido 10, 100, 1.000. • Uso de cálculos conocidos para resolver otros. • Uso de diferentes descomposiciones de los números para resolver multiplicaciones. • Uso del resultado de multiplicaciones conocidas para resolver otras. • Uso de resultados de la tabla pitagórica para resolver divisiones. • Uso de las descomposiciones de los números para resolver divisiones. En 4.º grado, la intención es elaborar un algoritmo para la técnica de la división. En estas páginas se comienza con la división por una cifra. En el capítulo 5 se continúa con esta elaboración y se plantea una división por dos cifras. Para acercarnos a la división desde lo intranumérico, descontextualizando el cálculo, se propone el análisis de diversas escrituras para los pasos intermedios del algoritmo y el trabajo con la estimación de resultados. En las preguntas del Para conversar juntos: “¿En qué se parecen las cuentas de Paula y Ángela? ¿Y las de Ignacio y Ángela? ¿En qué se diferencian estas últimas?”, se requiere una oportuna gestión del docente, con intervenciones que acompañen la búsqueda que hacen los chicos. Geometría El trabajo geométrico de este capítulo tiene por objetivo la elaboración y la sistematización de las propiedades de los triángulos. Al retomar el juego de adivinar la figura, ahora con la dificultad de que todos son triángulos, favorecemos la mirada sobre algunos aspectos que queremos enfocar: los ángulos y los lados. Este hacer geométrico que transitamos en los capítulos implica momentos de construcción, discusión, validación y conceptualización. Como dijimos antes, es importante permitir que los procedimientos y las hipótesis de los chicos se manifiesten sin darles un formato previo para que puedan elaborar progresivamente los objetos geométricos. En esta elaboración, con la intervención del docente, irán logrando conceptualizaciones parciales que se convertirán en el saber previo de las actividades de los próximos capítulos. Por ejemplo, en la conceptualización de los distintos cuadriláteros, el trabajo en torno a los triángulos se vuelve muy relevante. El enunciado de los elementos del triángulo y su uso para la clasificación ha de ser posterior al uso durante el juego y las actividades: es el corolario de la construcción del concepto que se propone a través de las actividades y no el punto de partida. Hay que tener en cuenta que las construcciones mediante instrumentos geométricos son indispensables para la mejor representación de las figuras. Es necesario avanzar en la caracterización de las figuras a partir de las relaciones observables en ellas. Cuanto mejor sea la representación, más fácil será avanzar en las definiciones. En un Para conversar juntos se propone: “¿Qué preguntas harían para poder adivinar cada una de las figuras? Elijan uno de los triángulos dibujados. Escriban pistas y dénselas a un compañero para que pueda descubrir de cuál se trata.” Este pedido de redactar las preguntas y las respuestas o pistas es un paso más en la definición de las figuras, porque el chico debe cumplir ambos roles: el del que pregunta y el del que responde. Los conocedores 13 5 Números naturales División Triángulos Numeración El propósito del juego que está planteado al inicio de este capítulo es el tratamiento del sistema de numeración decimal y de los números naturales. Este juego permite evidenciar habilidades y saberes acerca de la lectura y la escritura de números, la descomposición de números basada en la organización posicional y decimal del sistema, las relaciones aditivas y multiplicativas que subyacen a un número y la expresión de un número en términos de unidades, decenas y centenas. El cuadro que hay que completar en la página que sigue al juego permite la problematización de algunos conceptos matemáticos que queremos sistematizar en este momento: el sistema de numeración decimal, la lectura y escritura de números, y la expresión de un número en términos de unidades, decenas, centenas, etc. Para lograr este tipo de aprendizaje y esta sistematización se requiere la intervención estratégica del docente. Por eso, los problemas que se le plantean al alumno y la manera en que el docente organiza y conduce la actividad tienen que poder motivar a los niños a indagar entre sus saberes previos para decidir qué les conviene hacer, es decir, cuáles de los conocimientos de los que dispone puede utilizar en su solución. Operaciones: resolución de problemas En las páginas de resolución de problemas, tanto en El bazar de Jorge como en Los tejidos de Silvia, se continúa poniendo atención en el tratamiento de la información en torno a los problemas del campo multiplicativo, con situaciones de proporcionalidad, reparto y partición, y situaciones que combinan diferentes operaciones con números naturales. Se pone el foco en un trabajo específico con el análisis del resto y en el comienzo de la construcción del concepto de proporcionalidad directa. Las dos situaciones de El bazar de Jorge recuperan, además, el trabajo con estrategias de cálculo mental hecho en capítulos anteriores. Los objetivos de los apartados Para conversar juntos de estas páginas son mirar diferentes soluciones junto con otros, generar la posibilidad de descentrar la mirada de la propia producción, observar con más objetividad lo hecho por uno mismo, y analizar los procedimientos y las estrategias de los compañeros. Desde el punto de vista del aprendizaje matemático estas prácticas en el aula generan avances sobre los conocimientos y su interrelación: el comportamiento de los números, las relaciones entre ellos, las operaciones posibles, la diversidad de caminos de resolución, etc. Por otra parte, en un enfoque que toma en cuenta la construcción del 14 Los conocedores saber matemático, el pedido por la validación posterior al hacer, la reflexión sobre la propia acción y la argumentación basada en lo hecho son fundantes del avance progresivo. Hay que tener en cuenta que, cuando hablamos de saberes previos, nos referimos no solo a los que los chicos ya tienen, sino también a la actualización que puedan hacer de esos saberes para encarar la nueva situación. Los chicos deberían saber en qué viejos conceptos pueden apoyarse, e ir estableciendo qué relaciones existen entre la división, la multiplicación, la suma y la resta. Es función de la escuela favorecer el trabajo con diferentes situaciones y contextos que permitan a los chicos aprender a distinguir cuál es la operación o las operaciones que resuelven cada situación. En Los tejidos de Silvia los problemas contemplan situaciones variadas: la relación entre dividendo, divisor, cociente y resto; el análisis del resto; la posibilidad de dar más de una respuesta y de pensar las respuestas desde lo matemático y también incluir el contexto. En estas páginas, además, seguimos ocupándonos del avance en la construcción del concepto de división y, entre otros aspectos, hacemos foco en el hecho de que un chico se encuentre con la posibilidad de resolver diversos problemas mediante la división, por ejemplo, que encuentre que la división le permite: • averiguar en cuántas partes se puede repartir una cantidad dada y saber cuánto le corresponde a cada una (problemas de partición); • averiguar cuánto le corresponde a cada parte dentro de un reparto (problemas de reparto); • analizar qué sucede con el resto, donde se pone en evidencia que el resultado de la cuenta no es siempre la respuesta al problema; • estimar el cociente para favorecer el control de los resultados; • hacer cálculos en los que emplea sus conocimientos sobre la descomposición de números y la multiplicación por la unidad seguida de ceros. El objetivo de la actividad 3 (“Para resolver los problemas anteriores, Eloísa anotó estas cuentas. Complétenlas y anoten a qué datos se refiere cada número.”) es que los chicos puedan poner nombre a cada uno de los elementos del algoritmo de la división según el contexto del problema. Este trabajo apunta a evitar que no sepan dar la respuesta al problema, aunque hagan bien las cuentas. Operaciones: estrategias de cálculo En el capítulo anterior puntualizamos que en el Primer ciclo los chicos exploran diversas estrategias heurísticas para resolver una división. Es un objetivo de 4.º grado comenzar a utilizar el algoritmo convencional. Es necesario transitar por diversas estrategias de cálculo mental antes de “registrar” el algoritmo como el procedimiento óptimo para encontrar el resultado de una división. En el capítulo anterior se trabajaron las estrategias más significativas para abordar la construcción del algoritmo. En este capítulo avanzamos hacia el análisis del algoritmo de la división por dos cifras. Si bien las estrategias de cálculo necesarias en este algoritmo intermedio son las mismas para una, dos o cualquier cantidad de cifras del divisor, es conveniente avanzar con cierta lentitud para garantizar la solidez de las construcciones en el dominio de este hito social que es “aprender la cuenta de dividir”. No solo se ofrecen para el análisis cuentas completas, sino que además están desplegados los cálculos mentales que se fueron haciendo para resolverlas. Cuando se plantea un trabajo en el aula sobre las estrategias de cálculo mental, para que esta práctica se desarrolle en condiciones que la vuelvan potente, hay que considerar algunos puntos. • Saber que el cálculo mental permite trabajar con los números en un contexto intramatemático, es decir, sin otros contextos que den sentido. Si bien el juego es una buena estrategia para trabajar con el cálculo mental, después de jugar hace falta una reflexión que avance hacia la descontextualización de las jugadas. • Permitir las anotaciones. El lápiz y el papel facilitan pensar las soluciones, ensayar procedimientos, registrar pasos y resultados intermedios. Las anotaciones se convierten en la base desde la cual partir para comunicar. • No es posible pensar el trabajo con las estrategias de cálculo con la lógica del tema dado. En cambio, se ha de volver a esa estrategia tantas veces como hagan falta: con un juego, con cálculos para reflexionar, con desafíos y, cada vez, adaptándose a los progresos que el grupo y cada alumno vayan haciendo. Como el aprendizaje no es lineal, estas propuestas deben ser flexibles en cuanto a los tiempos y a los logros. • Es necesario planificar secuencias en torno a una estrategia, organizar una progresión de aprendizajes y no trabajar las clases de manera aislada. • Hay que tener en cuenta que los tiempos de adquisición de estrategias de cálculo mental se dan a mediano y a largo plazo. Lo que puede ser evidente para un niño puede ser incomprensible para otro. Hay un aprendizaje que se logra por un tipo de práctica sostenida en el tiempo, poniendo reiteradamente la mirada sobre ciertas regularidades. Geometría En este capítulo damos entrada especialmente a determinadas prácticas matemáticas que permiten el avance en el uso de lenguaje específico y en la elaboración de instructivos para realizar construcciones geométricas. A lo largo de la escolaridad el niño va diferenciando dibujo de figura. El dibujo es una representación de la figura, del objeto geométrico. Hace falta un trabajo que logre que se observen mejor en el dibujo las propiedades de la figura que ese dibujo representa. Se les pide a los chicos que realicen las construcciones ajustándose a ciertos datos o utilizando determinados instrumentos. Esto tiene varios propósitos, a saber: • Que los chicos comiencen a evidenciar la necesidad de fijar algunos datos, por ejemplo, ciertas medidas para la construcción de un único triángulo. • Que determinen si con los datos dados alcanza para fijar la construcción de un único triángulo o de varios. • Que determinen criterios para la construcción de un único triángulo y puedan elaborar institucionalizaciones parciales del estilo de “para construir un único triángulo se deben conocer la medida de dos lados y el ángulo comprendido” o “para construir un único triángulo es necesario conocer la medida de los tres lados”. • Que decidan cuáles son los instrumentos adecuados para la construcción solicitada. • Que construyan o identifiquen pistas para adivinar triángulos haciendo uso de la clasificación de los triángulos. • Que conjuguen las dos clasificaciones; por ejemplo, que indiquen si es posible que un triángulo sea rectángulo y escaleno. • Que al observar que no todas las construcciones son posibles, elaboren hipótesis que los acerquen a la propiedad triangular, es decir, que la condición necesaria y suficiente para que sea posible la construcción de un triángulo es que la medida de cada lado sea menor que la suma de las medidas de los otros dos lados. Hay dos instructivos en el capítulo: el de la construcción de triángulos, que recupera el uso de la circunferencia como auxiliar matemático y el de la copia de un ángulo con regla y compás, que vuelve sobre un contenido trabajado en el capítulo 2, ahora con la complejidad de seguir un instructivo y de que está al servicio de la caracterización de las figuras. Los conocedores 15 6 Fracciones Divisibilidad Cuadriláteros Numeración Las fracciones conforman el conjunto de los números racionales, al igual que los números decimales, que son fracciones decimales. Para construir el concepto de fracción los chicos tienen que encontrarse con la posibilidad de resolver diversos problemas mediante el uso de fracciones e identificar que una fracción puede ser la expresión de una relación entre la parte y el todo, el resultado de una situación de reparto, el resultado de una medición. Estos son los significados del concepto de fracción que se abordarán en 4.º grado. El concepto de fracción es central en el Segundo ciclo. Por eso, es indispensable definir qué aspectos deberán ser abordados en cada año del ciclo, tomando en cuenta el avance en la complejidad del objeto matemático. En 4.º grado es necesario centrarse en el concepto de fracción y en ciertas estrategias de cálculo que confluyen en la construcción del concepto, ya que un buen trabajo sobre el concepto crea una base sólida para todos los contenidos relacionados con fracciones. Por eso, le dedicaremos mucho espacio a ese trabajo y, en un principio, menos espacio a otra clase de operaciones relacionadas con las fracciones que implican estrategias más avanzadas. La entrada al concepto en este capítulo se plantea en relación con la división, a partir de situaciones de reparto. El resto del capítulo continúa con temas relacionados con la división. En los capítulos 7 y 8, se sumarán situaciones que permitan componer una cantidad a partir de otras expresadas en fracciones, utilizar fracciones para medir longitudes, comparar fracciones, hacer cálculos mentales con fracciones y, finalmente, sumar y restar fracciones. Se inicia el trabajo de análisis del resto en los repartos y particiones equitativas buscando la identificación de situaciones de reparto en partes iguales en las que tiene sentido repartir el resto, con la intención de ver si es posible repartir el resto y, de ser posible, cómo puede hacerse el reparto. Los problemas buscan producir la aparición de algunas fracciones, algunas más conocidas, otras menos: los medios, los cuartos, los tercios y los quintos. Es posible que algunos resuelvan los problemas con dibujos, escribiendo expresiones con palabras y no con números, o con expresiones fraccionarias poco convencionales como la mitad de 1/2. Operaciones: resolución de problemas En La florería de don Carlos se presentan situaciones para el tratamiento de la divisibilidad en el conjunto de los números naturales. En relación con este tema se 16 Los conocedores trata el estudio que se lleva a cabo sobre las divisiones exactas y las conclusiones que surgen de ese estudio. Este es un tema que se inicia en 4.º grado con un primer abordaje y se continúa en 5.º grado y en 6.º grado con mayor carga teórica. El estudio de los conceptos asociados a la divisibilidad permite la investigación de relaciones entre números, especialmente el análisis del algoritmo de la división, al que se le dedica también un espacio en la parte de estrategias de cálculo de este mismo capítulo. En 4.º grado se comienza el trabajo con los conceptos de múltiplo y de divisor de un número; y con las relaciones entre cociente, divisor, dividendo y resto. Un paso muy importante en el trabajo con la resolución de problemas y el tratamiento de la información es que los chicos vayan desarrollando habilidades en relación con la validación de sus producciones y la confrontación de la solución a la que llegaron con las de sus pares. Esta validación ha de enmarcarse en un espacio generado especialmente por el docente, un espacio que favorezca la discusión y el análisis de los procedimientos para ver si son adecuados y convenientes. De este modo, los chicos se van aproximando a la conceptualización de un determinado contenido y son capaces de distinguir qué procedimientos son válidos y eficaces, y cuáles no lo son. Los modos de resolución y los procedimientos que los chicos emplean para abordar un problema muestran, en parte, el sentido que para ellos tiene esa situación y los significados que hasta el momento han podido construir. Por eso, hace falta poner atención tanto en los problemas que seleccionamos como en el relevamiento de los diversos procedimientos que los chicos van desarrollando en la clase para resolverlos, ya que este relevamiento nos permitirá seleccionar lo que ofreceremos a la reflexión en las puestas en común para provocar, en el tiempo, el progreso de los conocimientos. Operaciones: estrategias de cálculo El título que inicia el trabajo en este eje es Pensar las cuentas de dividir, porque el trabajo en estas páginas con la división entera de números naturales va a estar centrado en propuestas para “acortar” la resolución del algoritmo intermedio por 1 y 2 cifras, en función de las estrategias de cálculo que fueron trabajadas con la multiplicación. Como la división es un concepto muy complejo, es necesario continuar trabajándolo con los chicos a lo largo de toda la escolaridad primaria. Hemos visto que va mucho más allá del algoritmo tradicional de la cuenta de dividir. Por eso, se proponen Más estrategias para dividir mentalmente, estrategias de cálculo que tienen validez en sí mismas y que, al mismo tiempo, complementan y sostienen el trabajo con el algoritmo. El objetivo de la actividad 11 es el encuadramiento, es decir, que se refiere a poder decidir en qué intervalo numérico se encuentra un cálculo. Un aspecto fundamental del cálculo –no solo del cálculo mental– es la posibilidad de estimar, redondear, aproximar, ya que, cada día, la mayoría de los cálculos que se hacen fuera de la escuela son mentales y muchas veces la respuesta no tiene por qué ser exacta: alcanza con una aproximación o estimación. Incluso cuando se utiliza la calculadora debemos asegurarnos de haber tecleado bien los datos y, para ello, hay que contrastar el resultado con la estimación del resultado. El desafío que se ofrece en estas páginas es un tema central de trabajo en 5.º grado e implica la relación entre el dividendo, el divisor, el cociente y el resto. Geometría Este es el último capítulo en el que se ven temas de geometría, ya que los capítulos siguientes están centrados en la medida. Las páginas de geometría de este capítulo no solo abordan el trabajo sobre los cuadriláteros, sino que dan una vuelta más al tema de las construcciones, a partir de todo lo que se vino trabajando desde el capítulo 1. Por eso, hay títulos referidos a los cuadriláteros, como Los elementos y la clasificación de los cuadriláteros y Construcción de cuadriláteros, y títulos referidos a otras construcciones: Rectas paralelas y perpendiculares y Más construcciones de triángulos, en las que se comienza un trabajo que será más fuerte en 5.º y en 6.º: la exploración de las relaciones entre los ángulos interiores. En el Segundo ciclo se comienza con la construcción de cuadriláteros. Se abre el tema en 4.º grado, contactando con los saberes previos del trabajo con figuras; se lo continúa fuertemente en 5.º grado; y se lo trata de manera breve en 6.º grado para adentrarse en los polígonos. El objetivo de las actividades propuestas en este capítulo es el avance en la identificación de las propiedades que caracterizan a cada uno de los cuadriláteros, considerando los lados y los ángulos, que permitirán definirlos. El comienzo de esta parte del capítulo remite al juego de adivinar la figura. Esta vez la pista que se ofrece al análisis incluye la relación de perpendicularidad. Esta actividad es otro buen ejemplo de cómo la misma dinámica del juego de adivinar la figura se puede ir complejizando de tal manera que sea útil para abordar cualquier figura. Utilizar el mismo juego, con las variaciones de las figuras en torno a las cuales se está trabajando, permite a los chicos centrarse en el trabajo sobre el objeto matemático específico, ya que la dinámica del juego es conocida y no lleva ni tiempo ni energía especial aprenderla. En estas páginas se definen los cuadriláteros en función de si tienen solo un par de lados paralelos o dos pares. No todos los textos plantean esta definición, que clasifica los cuadriláteros en trapecios, paralelogramos y cuadriláteros que no tienen ningún par de lados paralelos (trapezoides). El cuadrado es rombo y es rectángulo; los cuadrados, los rectángulos y los rombos son paralelogramos. Al igual que en las construcciones de triángulos del capítulo 5, el pedido de estas construcciones se ajusta a ciertos datos o al uso de determinados instrumentos, porque tienen variados propósitos. Uno de estos propósitos es el avance en la identificación de las propiedades que caracterizan a los cuadriláteros, considerando los lados y los ángulos. Otro propósito es discutir acerca de los elementos necesarios para construir un único cuadrilátero; acerca de cuáles son los elementos que fijan la forma y el tamaño, y que los chicos puedan decir si, dados ciertos datos, es posible o no construir infinitos cuadriláteros (en clase se hablará “muchos cuadriláteros”), y acerca de qué datos son necesarios para la construcción de un paralelogramo y qué es necesario indicar para que el cuadrilátero sea único. El desafío acerca de cuántos cuadrados hay en la figura tiene como uno de sus objetivos principales el desarrollo de habilidades específicas para la resolución de problemas, ya que no siempre basta con la primera mirada para la resolución de un problema. Resulta necesario identificar una estrategia óptima para la resolución de la situación (en este caso, para el conteo de la cantidad de cuadrados); por ejemplo, la identificación de regularidades. Los juegos y desafíos –no solo los de este capítulo– favorecen el desarrollo de habilidades para comprender conceptos y el lenguaje específico matemático, identificar analogías y diferencias, seleccionar datos y procedimientos correctos, cambiar una metodología de trabajo cuando la que se está utilizando “no sirve” y, fundamentalmente, colaboran en el desarrollo de una actitud positiva hacia la Matemática. Los conocedores 17 7 Fracciones Instrumentos de medición Tiempo En este capítulo se propone trabajar con las fracciones tanto en el eje de numeración como en los ejes de operaciones. Numeración En Las fracciones el foco del trabajo con el concepto de fracción está puesto en las representaciones, el aspecto gráfico, las relaciones, la comparación de fracciones y la reconstrucción de la unidad usando fracciones. El recuadro teórico está al comienzo, una situación muy poco común. Esto es así porque brinda una información necesaria para resolver la actividad 1 y útil en las actividades 2, 3 y 4. Al mismo tiempo, sintetiza el trabajo comenzado en el capítulo 6. La actividad 6 plantea una situación diferente de las anteriores, ya que no hay un entero sobre el que tomar decisiones: se presenta una parte y hay que reponer el entero. Es posible que algunos chicos tomen cada dibujo como el entero. Para facilitar la lectura de que cada dibujo es la mitad se ofrecen formas variadas, como la inclusión de un medio circulo. Al reconstruir el entero es posible hacer dibujos diferentes. El objetivo del Para conversar juntos que se encuentra a continuación de la actividad 6 (“¿Hay más de un dibujo posible? Compartan los dibujos que hicieron.”) es que, al compartir, los alumnos puedan validar el entero que cada chico reconstruyó y que, aunque los dibujos de cada uno sean diferentes, todos puedan ser vistos como enteros equivalentes si respetan la cantidad de partes. Bajo el título Las fracciones en la recta numérica, se trabaja la representación de fracciones en la recta numérica y se da otra vuelta al concepto de fracciones equivalentes. Como los niveles de dificultad con la recta numérica varían mucho de chico a chico, es conveniente haber trabajado en el contexto de los números naturales con algunos aspectos que presentan dificultad en su uso, porque, al ser ya conocida, se convierte en un excelente instrumento para avanzar en el concepto de fracciones y para comenzar a introducirse en el concepto de densidad de los números racionales, que se amplía y se profundiza en 5.º y en 6.º. Sugerimos que el docente observe las posibilidades de su grupo de alumnos mientras los deja explorar la recta, y que acompañe y guíe el debate posterior. El objetivo de las actividades de Fracciones equivalentes es constatar que, aunque un entero esté partido en diferente cantidad de partes, las fracciones que expresan una parte pueden ser equivalentes. Es el caso de la actividad 9, en la que se pide que pinten fracciones 18 Los conocedores equivalentes a 1/2 y los enteros están partidos en cuartos, sextos, octavos y décimos. En la actividad 11, se busca que identifiquen que se trata de la misma cantidad y viene a continuación de un pedido de expresar 1/3 en sextos, aclarando que se trata de “la misma cantidad de agua”. Operaciones: resolución de problemas En estas páginas nos adentramos en una reflexión que tiene una fuerte presencia en muchas de las actividades y problemas que se plantean con fracciones: cuando trabajamos con fracciones, es muy importante tener presente la unidad. En Las fracciones y la unidad, además, se abordan los conceptos de cantidad continua y cantidad discreta. Son tres situaciones que plantean diferentes casos en relación con la unidad. En la primera situación, 3 y 1/3 representan la misma cantidad de escalones, porque ambos tomaron unidades diferentes: la señora considera que los 9 escalones son la unidad y Jorge considera a cada escalón como una unidad. En la segunda situación, 1/2 y 2/4 también representan la misma cantidad. Esta situación refiere al uso de fracciones en el contexto de un uso social de las medidas de capacidad. Los escalones están separados, pero, en cambio, no se puede separar el líquido en partes y contarlo: es una cantidad continua. Para resolverla, los chicos pueden recurrir a gráficos o dibujos, o a un cálculo mental. En la tercera situación, 1/2 es la mitad para ambos, pero representa cantidades diferentes de monedas, porque las unidades que sirven de base para calcular 1/2 son diferentes. Operaciones: estrategias de cálculo En 4.º grado definiremos la fracción a partir de situaciones de reparto y progresivamente se irán sumando situaciones que permitan componer una cantidad a partir de otras cantidades expresadas en fracciones, comparar fracciones, hacer cálculos mentales con fracciones, utilizar fracciones para medir longitudes, y sumar y restar fracciones. En estas páginas se continúa con la relación entre las partes y los enteros. Se propone encontrar la fracción de un entero según sean magnitudes continuas o discretas y diferentes representaciones de algunas fracciones. Las operaciones con fracciones se continúan trabajando desde la perspectiva del cálculo mental y no de la del cálculo algorítmico. Cuando hablamos de cálculos algorítmicos con fracciones, pensamos, por ejemplo, en el algoritmo conocido en la escuela para obtener fracciones equivalentes (multiplicar o dividir el numerador y el denominador por un mismo número) o al uso de este algoritmo en las operaciones de suma y resta de fracciones de distinto denominador. El cálculo mental, por el contrario, se define como un conjunto de procedimientos que no refieren a un algoritmo –conjunto de estrategias y procedimientos que va desplegando el que los hace a partir del análisis de los datos con los que cuenta–, y que se utilizan para obtener resultados exactos o aproximados. Las estrategias pueden ser muy diversas y no se espera un único camino posible para llegar a la resolución. En Armar un entero se trabajan las relaciones entre fracciones, la reconstrucción de la unidad usando fracciones y qué fracción es necesario sumar o restar a una fracción dada para obtener un entero. En Armar enteros mayores que 1 el tema de estudio es qué fracción es necesario sumar a una fracción dada para obtener enteros mayores que uno. En Comparar fracciones nos adentramos en las estrategias de cálculo para comparar fracciones. Una de estas estrategias de cálculo es considerar si la fracción equivale a un entero, o es mayor o menor que un entero. Las situaciones presentadas en la actividad 12 están contextualizadas, mientras que las presentadas en la actividad 14 no lo están y los chicos pueden recurrir a cálculos mentales que impliquen la relación entre el numerador y el denominador. En esta parte del capítulo, la mirada comienza a dirigirse hacia la relación entre el numerador y el denominador. Todavía hay textos escolares en los que se lee la clasificación de las fracciones en propias (el numerador es menor que el denominador), impropias (el numerador es mayor que el denominador) y aparentes (la relación entre numerador y el denominador da como resultado un entero igual o mayor que 1). En cambio, pensar en una clasificación de las fracciones como menores que 1, iguales a 1, mayores que 1 y equivalentes a un entero, facilita el trabajo de comparación y nos ubica en un contexto que posibilita la resolución de situaciones. Tengamos nuevamente en cuenta que es fundamental generar un espacio que favorezca el trabajo colectivo de reflexión y de análisis de los problemas planteados –sobre todo con la descontextualización que implican los que aquí proponemos–, para promover la comunicación y la explicitación de las distintas conclusiones y la observación de cuáles son los conocimientos de los que parten los chicos y cuáles los que utilizan. Medida En este capítulo comienza una serie (capítulos 7, 8 y 9) en la que el eje es la medida. Sugerimos al docente relevar los saberes previos de sus alumnos y las experiencias realizadas en torno a la medida en el Primer ciclo antes de iniciar el trabajo con las situaciones propuestas en este capítulo. Este relevamiento tiene por objetivo considerar si es posible comenzar directamente con el tema o si hace falta comenzar por algo que permita a los alumnos recuperar algunas ideas centrales sobre los problemas de la medición. El trabajo con la medida tiene que contemplar estos puntos: • El hecho de medir, el concepto de medida. • El concepto de magnitud. Todo lo que puede medirse recibe el nombre de magnitud. • Los instrumentos que se utilizan y para qué son apropiados. • Las unidades de medida cotidianas y más accesibles. • Las equivalencias posibles a partir de las unidades de medida vistas durante las actividades que se proponen. • El uso de fracciones en el contexto de la medida: 1/2, 1/4, 3/4. • La estimación de una medida. A partir de las actividades de este capítulo y de los siguientes, se recuperará que: • Medir es elegir una unidad y determinar cuántas veces entra en el objeto que se mide. • El resultado de la medición depende de la unidad elegida. • Al medir, muchas veces hace falta fraccionar, partir la unidad de medida elegida (“mide 1 1/2”). • La elección de las unidades de medida depende del objeto que se va a medir. • La medición siempre es aproximada; sin embargo, hay instrumentos y procedimientos que garantizan una medición de mayor exactitud. • Para cada magnitud son adecuados diferentes instrumentos de medida. En el caso de la medición del tiempo, la intención es que se tome la noción de tiempo como una magnitud. Esto implica identificar unidades de medida y también instrumentos de medición. Dada la complejidad de las nociones relacionadas con la medición del tiempo, la intención es que los chicos de 4.º grado vayan realizando un trabajo superador respecto del iniciado en el Primer ciclo. Los conocedores 19 8 Fracciones Longitud, peso y capacidad En este capítulo se continúa el trabajo con las fracciones tanto en el eje numeración como en los ejes de operaciones. Numeración La recta numérica es un instrumento muy interesante para avanzar en la representación y en la comprensión del sistema de numeración y, al mismo tiempo, ofrece algunas dificultades a muchos chicos. Hemos recorrido algunos puntos que se deben tener en cuenta desde que fue usada en el capítulo 4 para ubicar números naturales, hasta la propuesta en el capítulo 7 de ubicar fracciones del mismo denominador y la introducción del tema de las equivalencias. En este capítulo aumenta la complejidad, ya que el pedido es ubicar fracciones con distinto denominador. Ahora bien, si observamos las diferentes dificultades que se van sumando –el uso de la recta en sí misma, las fracciones, la equivalencia– tenemos más posibilidades de pensar propuestas para ubicar fracciones que presenten una dificultad creciente pero que no “den un salto”. Esto significa que, si bien las fracciones pueden tener distinto denominador, es conveniente que se encuadren o bien entre fracciones equivalentes sencillas (medios y cuartos, quintos y decimos), o bien entre fracciones que presenten cierta facilidad para dividir el intervalo (tercios, sextos y novenos). Esta es precisamente la propuesta de Más fracciones en la recta numérica. El desafío que se encuentra varias páginas más adelante en este capítulo es un desafío en 4.º grado porque pide la ubicación en la recta de fracciones para las que hay que dividir el mismo intervalo en forma muy diferente: tercios y medios. Otra actividad que aumenta la complejidad del uso de la recta numérica y pone en evidencia la construcción que se ha venido haciendo del concepto de fracción es pedirles que, dada una fracción, ubiquen enteros, o que señalen en la recta las fracciones representadas por una marca. En este último caso, en la actividad 4, “¿qué fracción corresponde escribir en el primer punto de la recta? ¿2/3? ¿4/6? ¿8/12?”. Estos denominadores son más sencillos de representar por los cuadraditos de la hoja (que fueron colocados para facilitar la relación). Pero también es posible escribir cualquier otro denominador, y este es un debate muy interesante de mantener con el grupo. La notación decimal y la notación fraccionaria no permiten un reconocimiento inmediato del mismo número expresado de ambas formas. No es inmediatamente reconocido el número que está expresado, por 20 Los conocedores ejemplo, en 1/4 y en 0,25. Tomando esto en consideración se proponen en el eje Medida actividades que implican ir pensando las relaciones entre la notación decimal y la fraccionaria. Operaciones: resolución de problemas El tema de estas páginas es la suma y la resta de fracciones, y una introducción a la multiplicación de fracciones. En la primera situación de La huerta, es necesario responder una pregunta que implica realizar, en un primer paso, una suma de fracciones de distinto denominador y, luego, una resta. La intención es que los alumnos puedan apelar a las estrategias de cálculo mental y a la búsqueda de fracciones equivalentes que vienen trabajando desde el capítulo 6. Por lo tanto, el objetivo no es que todos usen el procedimiento algorítmico para sumar y restar fracciones. El cálculo algorítmico es una serie de reglas que se utilizan y se aplican en un orden preestablecido, siempre el mismo y del mismo modo, independientemente de cuáles sean los números que estén en juego, como una forma de garantizar que se alcance el resultado buscado en un número finito de pasos. En este sentido, si algún alumno usa el cálculo algorítmico (sea un procedimiento reflexionado o mecánico), se lo trata como un procedimiento más que se verá cuando sea el momento de compartir cómo se resolvió el problema. De hecho, al trabajar este tema en estrategias de cálculo, se proponen varias estrategias para resolver sumas y restas. En la segunda situación de La huerta se trata de hallar la mitad del terreno que se pensaba utilizar para plantar la lechuga: 1/2 de 3/8. Con esta situación, estamos entrando en el terreno de la multiplicación de fracciones, un tema que plantea un verdadero desafío a los alumnos de 4.º. Es importante que el maestro seleccione buenos problemas, que esté atento a los procedimientos que utilizan los alumnos para resolverlos y que proponga actividades que provoquen la evolución de esos procedimientos y la construcción de nuevos significados. Pero hay que tener cuidado de no apresurarse a institucionalizar lo que aún no está sólidamente construido. Por eso, decimos que se trata de una introducción a la multiplicación de fracciones. Es fundamental permitir que cada chico resuelva las situaciones según sus posibilidades y saberes, y que el avance se vaya dando al compartir con otros las estrategias y los procedimientos, al reflexionar juntos sobre lo hecho, en el marco de oportunas intervenciones docentes. Operaciones: estrategias de cálculo Al inicio del trabajo sobre el eje en este capítulo hay situaciones contextualizadas en las que se trata de sumar y restar para encontrar la respuesta. En las páginas de resolución de problemas, se propuso una reflexión sobre la situación allí planteada y las posibles resoluciones. Ahora se trata de estar atentos a lo que cada alumno pudo ir elaborando de lo conversado en forma grupal. La escritura de los pasos que utilicen, los cálculos que hagan, la forma de escribir con fracciones o no estos procedimientos quedan librados a cada chico. Es esperable que los chicos se apoyen en las relaciones entre fracciones que se vienen tratando desde el capítulo 6 y en las estrategias de cálculo mental que fueron recorriendo. Por ejemplo, en la actividad 19 a se trata de una suma simple: 2/6 + 1/6; la b, además de que hay que hacer 3/4 + 3/4 = 6/4, como es posible responder “comieron 6/4 de tarta” o “comieron 1 tarta y 1/2”, se convierte en una situación interesante para debatir. En la actividad c se pueden usar fracciones equivalentes. En la d, pueden usar todo lo aprendido en relación con completar un entero y, entonces, pensar 4/4 – 1/4 = 3/4 o 1/4 + ... = 4/4. En la e se incursiona en la multiplicación de fracciones, ya que la respuesta implica calcular 1/4 de 3/4. La f pide pensar nuevamente en fracciones equivalentes o en una representación gráfica. La representación gráfica probablemente sea una forma de resolución que usen los chicos para varios de estos problemas. De hecho, se pregunta por este procedimiento en el Para conversar juntos (“¿Cómo resolverían gráficamente la siguiente suma: 5/6 + 2/3?”). Y después de analizar dos situaciones mediante ese procedimiento, se les pide a los chicos que resuelvan gráficamente, juntos, las situaciones restantes. La actividad 20 plantea directamente los cálculos descontextualizados. El objetivo es que los alumnos puedan recurrir a distintas estrategias entre todas las tratadas desde el capítulo 6, en función de los números que intervienen en cada cálculo. Medida El trabajo con las medidas en 4.º se puede iniciar en el marco de lo realizado en el Primer ciclo: la realización efectiva de mediciones de longitud, de capacidad y de peso usando unidades no convencionales e identificando progresivamente el hecho de que medir requiere el uso de unidades convencionales. El concepto de magnitud fue trabajado en el capítulo anterior. En este capítulo, el eje se aborda en seis páginas, dos por cada magnitud: longitud, peso, capacidad. Con cada magnitud se propone el mismo trabajo: ver unidades convencionales, y realizar estimaciones y comparaciones. En cuanto al trabajo con la medida, en algún momento la escuela ha dedicado mucho espacio a las unidades convencionales y a los pasajes entre unidades. Hoy se considera que es necesario darle a la estimación el espacio que merece. Por eso, desde el comienzo del trabajo con medida en el Primer ciclo se realizan estimaciones en función de las magnitudes, los instrumentos y las unidades de medida. Este trabajo es imprescindible porque permite hacer juicios subjetivos sobre diferentes medidas en situaciones cotidianas y, además, favorece el desarrollo de la capacidad de juzgar la razonabilidad de una medida, lo que da mucho fruto al momento de pensar los pasajes entre una unidad y otra. Para cada magnitud se proponen actividades de estimación; por ejemplo, que indiquen qué unidad es más útil para medir algo, que estimen cuánto miden ciertos objetos, que indiquen si coinciden las estimaciones que hicieron con las medidas que tomaron y que completen tablas con elementos que midan lo que se les indica en ella. Después de haber realizado las estimaciones, se les ofrece un momento para compartir lo hecho y reflexionar sobre ello en el Para conversar juntos. Este tipo de intervenciones del docente, como dijimos antes, son necesarias y apuntan a detenerse sobre un aspecto del hacer que a menudo es intuitivo y puede parecer de cierta obviedad, pero sin esa reflexión el avance queda librado a la posibilidad de cada uno. Es evidente que existe un tipo de conocimiento matemático que puede ser construido, adquirido o desarrollado fuera de la escuela, en diferentes contextos sociales y a través de diversas prácticas habituales en la cultura en la que se vive. La medida es buen ejemplo de esto. Si bien en la vida cotidiana ese conocimiento suele ser eficaz, es un conocimiento que, al mismo tiempo, desconoce las condiciones de su propia producción. El aprendizaje escolar es un aprendizaje que pide una organización de la tarea donde las metas, los contenidos, las actividades y la organización son muy diferentes de los de la vida cotidiana y complementan sus saberes. Los conocedores 21 9 Números decimales Perímetro y área En este capítulo, se entra de lleno en el trabajo con decimales, tanto en el eje de numeración como en los ejes de operaciones. Numeración Los números decimales son racionales. Ciertos aspectos de los racionales ya fueron tratados con las fracciones, pero las expresiones decimales presentan una complejidad que es nueva para los alumnos de 4.º grado. Los chicos han ido construyendo una serie de conocimientos numéricos durante los años anteriores de su escolaridad y, al enfrentarse con los racionales, se encuentran con que sus conocimientos tienen un dominio de validez limitado: el conjunto de los números naturales. En el terreno de los naturales es adecuado pensar en el número anterior y el posterior, por ejemplo, y este saber les permite a los chicos respuestas correctas a diversas situaciones. Pero ¿qué sucede cuando esta idea de anterior o posterior se aplica a otros dominios numéricos, como el de los números racionales? El uso directo de estos saberes produce errores que significan importantes pérdidas de sentido. Por ejemplo, “el siguiente a 1,3 es 1,4” o “1/3 + 1/2 es igual a 1/5”. Estos errores sistemáticos y persistentes tienen origen en un conocimiento anterior que se constituye en un aspecto que hay que observar, confrontar, ratificar o rectificar, y sobre el que hay que reflexionar y debatir, con el objetivo de lograr otros conocimientos. Como hemos dicho, las expresiones decimales son una forma de representar los números racionales y, por eso, mucho de lo trabajado con las fracciones se convierte en un saber recuperable para tratar los números con coma. La entrada al trabajo con decimales se ve facilitada cuando se la enfoca en relación con el dinero y el sistema monetario, un objeto de la vida cotidiana con el que a esta edad ya tienen contacto. Hay además una gran cantidad de portadores numéricos presentes en la vida en los que se leen expresiones decimales. Para resolver las situaciones los chicos pueden hacer dibujos de los billetes y de las monedas, pueden usar billetes de cotillón, pueden realizar cálculos, registrar escrituras en las que hay una cuenta o en la que se mezclan palabras y números. Como dijimos antes, es importante permitir que los procedimientos y las hipótesis de los chicos se manifiesten sin darles un formato previo para que puedan elaborar progresivamente los objetos matemáticos. En esta elaboración, con la intervención docente, irán logrando conceptualizaciones parciales que se convertirán en el saber previo de las actividades 22 Los conocedores de los años escolares posteriores. En las actividades de estas páginas los objetivos son que se enfrenten con escrituras decimales, establezcan la relación entre pesos y centavos, y décimos (las monedas de 10 centavos), interpreten escrituras, establezcan relaciones entre la lectura y la escritura de los decimales, interpreten la información que ofrece el número con coma, analicen que un mismo valor puede formarse de variadas maneras (usando diferentes monedas) y analicen la expresión numérica de las equivalencias establecidas. Una vez que se han explorado las relaciones entre los nombres y las escrituras, partiendo de los saberes previos de los chicos, se institucionalizan ciertos aspectos de la lectura y la escritura de los números decimales. Las situaciones presentan un desafío que pone a los chicos en situación de enfrentarse con el problema y buscar cómo resolverlo antes de conocer cómo se hace mediante una explicación recibida. En algunos de estos intercambios se les comenzó a pedir que “expliquen”. Es lo que ocurre, por ejemplo, en este Para conversar juntos: “Por un billete de un determinado valor, ¿siempre la cantidad de monedas de 50 centavos será el doble que las de $ 1? ¿Por qué? ¿Ocurre lo mismo con las de 10 y 5 centavos? ¿Cómo explican la relación entre la cantidad de monedas de $ 1 y las de veinticinco centavos para un billete del mismo valor?” Esto favorece la objetivación de un saber que cobra mejor forma al intentar ser explicitado. Luego, se continúa el trabajo con las hipótesis que tienen los chicos acerca de los números, representadas por lo que dicen los chicos de la página 139, y se propone un avance al compartir las estrategias que utilizan para la comparación y el ordenamiento. El desafío de la página 139 (“Escriban 3 números decimales entre 1,5 y 1,6. Escriban un número entre 2 y 3 que tenga 8 en la cifra de los décimos. ¿Cuál es el número que tiene 99 décimos y la cifra de los centésimos es 1?”), que es un desafío en 4.º grado, en 5.º es uno de los temas centrales de trabajo para abordar el concepto de densidad de los racionales. Lo consignamos a modo de ejemplo de la complejización año a año de los mismos temas y, al mismo tiempo, para observar el lugar y el tono de los desafíos presentados en los capítulos. Operaciones: resolución de problemas Los objetivos de las actividades propuestas en estas páginas son que los chicos sumen y resten decimales, e institucionalizar finalmente el algoritmo en relación con la suma. Cuando decimos finalmente, nos referimos a que lo que se esperaba es que antes resolvieran las actividades a partir de diferentes estrategias de cálculo: exacto, aproximado y mental. En las dos situaciones de Compras en el kiosco, se abordan la suma y la resta de números decimales y la multiplicación de un decimal por un natural. En el análisis de la primera situación la nena dice: “Podemos sumar primero la parte entera y después, la decimal”. En la segunda situación, se plantea un problema que puede ser resuelto con la suma o con la multiplicación. Hay aún algunos pasos que transitar antes de estar en condiciones de abordar el algoritmo de la suma de decimales. Por eso, se continúa con el planteo de situaciones en las actividades del siguiente eje. Operaciones: estrategias de cálculo En diversos momentos hemos planteado que el sentido de las operaciones es una construcción que está vinculada tanto a las situaciones problemáticas como a los procesos que llevan a su resolución, y que el sentido de las operaciones se construye paralelamente en el terreno de la resolución de los problemas y en el de las estrategias y recursos de cálculo. Recordemos también que la habilidad de calcular implica manejar propiedades relacionadas con la naturaleza de los números, con las reglas del sistema posicional decimal y, al mismo tiempo, con las propiedades de la operación en sí misma. Una vez hechas estas aclaraciones, miremos puntualmente el tema del cálculo en las situaciones de este eje. En En la librería se continúa trabajando con la estrategia de estimación en situaciones contextualizadas. El cálculo mental y el cálculo estimativo o aproximado son estrategias muy útiles cuando se trata de anticipar o de estimar rápidamente un resultado y son una buena herramienta de control de los propios resultados obtenidos a través de cálculos convencionales o algorítmicos, o incluso de la calculadora. La estimación y la aproximación se fortalecen con el juego Aproximando resultados. Los desafíos y los juegos con números presentan los cálculos de forma amena, muestran el aspecto recreativo de la Aritmética, permiten identificar propiedades numéricas, establecer relaciones y practicar operatoria en forma amena, interesante y desafiante. Además, es posible jugarlos en repetidas oportunidades y, de ese modo, observar el avance en el uso y en la elaboración de la estrategia. En Cuentas con coma se hace una primera aproximación a los algoritmos. Se presenta el de la suma y, a partir de los saberes que allí pueden haberse construi- do, se plantea una resta de números decimales y se propone compartir cómo piensan ese procedimiento. Los algoritmos con decimales son un tema fuerte de 5.º; en 4.º solo se inicia el trabajo. La mirada sobre los posibles errores favorece la reflexión sobre estos números, que han generado una ruptura tan fuerte en relación con los naturales. Medida En estas páginas se inician las primeras aproximaciones a los conceptos de perímetro y de área. En Cálculo de perímetros se plantean las situaciones y se cierra ese momento de trabajo con un Para conversar juntos (“¿Cómo hicieron para averiguar la medida de cada contorno? ¿Todos lo hicieron de la misma forma?”). Recién después se entra de lleno al tema con la institucionalización de la “formula” para hallar el perímetro. Azulejos en la cocina es la primera aproximación al concepto de área. El propósito es que los chicos empleen diferentes estrategias para resolver las situaciones: dibujar el plano de la pared pasado a centímetros, o pasarlo a centímetros, utilizar una hoja cuadriculada y contar los cuadraditos; utilizar azulejos dibujados y recortados a modo de material concreto o dibujar los azulejos sobre la superficie del plano. Es deseable que los chicos se apoyen en los conocimientos que tienen sobre las fracciones para poder indagar sobre ciertos resultados. En el caso de los conceptos de perímetro y de área resulta importante aproximarnos al de área y abordar la relación entre ambos. Los conocedores 23 Bibliografía sugerida para ampliar las discusiones planteadas bressan, a. (coord.), Contenidos básicos comunes para la egb - Matemática, Buenos Aires, Ministerio de Cultura y Educación de la Nación Argentina, 1995. brousseau, g., Fundamentos y métodos de la didáctica de la Matemática, Córdoba, Facultad de Matemática, Astronomía y Física, Universidad Nacional de Córdoba, 1987. brousseau, g., “Los diferentes roles del maestro”, en parra y saiz (comp.), Didáctica de las matemáticas. Aportes y reflexiones, Buenos Aires, Paidós, 1994. charnay, r., “Aprender (por medio de) la resolución de problemas” en parra y saiz (comp.), Didáctica de las matemáticas. Aportes y reflexiones, Buenos Aires, Paidós, 1994. chemello, g. (coord.), hanfling, m. y machiunas, v., El juego como recurso para aprender. Juegos en Matemática egb 2 (Material para docentes y recortable para alumnos), Buenos Aires, Ministerio de Educación, Ciencia y Tecnología, 2001. chevallard, i., gascón, j. y bosch, m., Estudiar Matemática. El eslabón perdido entre la enseñanza y el aprendizaje, Barcelona, Ice-Horsori, 1997. fuenlabrada, i., block, d., balbuena h. y carvajal, a., Juega y aprende Matemática. Propuestas para divertirse y trabajar en el aula, Buenos Aires, Novedades Educativas, 2000. lerner, d., La matemática en la escuela. Aquí y ahora, Buenos Aires, Aique, 1992. panizza, m., “Reflexiones generales acerca de la enseñanza de la Matemática”, en panizza, m. (comp.), Enseñar Matemática en el Nivel Inicial y el Primer Ciclo de la egb. Análisis y propuestas, Buenos Aires, Paidós, 2003. parra, c., sadovsky, p. y saiz, i., Matemática y su enseñanza. Documento curricular. ptfd (Programa de transformación de la Formación Docente), Ministerio de Cultura y Educación, 1994. parra, c., “Cálculo mental en la escuela primaria”, en parra y saiz (comp.), Didáctica de las matemáticas. Aportes y reflexiones, Buenos Aires, Paidós, 1994. parra, c. y saiz, i. (comp.), Didáctica de las Matemáticas. Aportes y reflexiones, Buenos Aires, Paidós, 1994. ponce, h., Enseñar y aprender Matemática. Propuestas para el Segundo Ciclo, Buenos Aires, Novedades Educativas, 2000. pujadas, m. y eguiluz, m. l., Fracciones, ¿un quebradero de cabeza? Sugerencias para el aula, Buenos Aires, Novedades Educativas, 2000. quaranta, m. e. y wolman, s., “Discusiones en las clases de matemática. Qué, para qué y cómo se discute”. En panizza, m. (comp.): Enseñar matemática en el Nivel Inicial y Primer Ciclo de egb, Buenos Aires, Paidós, 2003. 24 Los conocedores sadovsky, p., “¿Enseñar división es transmitir cultura?”, en La Educación en nuestras manos, n.° 54, marzo de 1999. saiz, i., “Dividir con dificultad o la dificultad de dividir”, en parra y saiz (comp.), Didáctica de las matemáticas. Aportes y reflexiones, Buenos Aires, Paidós, 1994. vergnaud, g., El niño, la matemática y la realidad: problemas de la enseñanza de las matemáticas en la escuela, México, Trillas, 1991. wolman, s., “Algoritmos de suma y resta: ¿por qué favorecer desde la escuela los procedimientos infantiles?”, en Revista del Instituto de Investigaciones en Ciencias de la Educación, iice, Facultad de Filosofía y Letras, Universidad de Buenos Aires, Buenos Aires, Miño y Dávila, 1999. Documentos curriculares para Nivel Primario Diseño Curricular para la Educación Primaria. Segundo Ciclo, Dirección General de Cultura y Educación de la Provincia de Buenos Aires, La Plata, 2008. En: http://abc.gov.ar/lainstitucion/organismos/consejogeneral/disenioscurriculares/default.cfm Diseño Curricular para la Escuela Primaria. Segundo Ciclo de la Escuela Primaria / Educación General Básica, Gobierno de la Ciudad de Buenos Aires, Secretaría de Educación, Dirección General de Planeamiento, Dirección de Currícula, Buenos Aires, 2004. En: http://www.buenosaires.gov.ar/areas/educacion/curricula/ primaria.php Documentos de actualización y desarrollo curricular del Gobierno de la Ciudad de Buenos Aires, Secretaría de Educación, Dirección General de Planeamiento, Dirección de Currícula. En: http://www.buenosaires.gov.ar/areas/educacion/curricula/ docum/matematica.php Núcleos de Aprendizajes Prioritarios. Segundo Ciclo EGB / Nivel Primario, Ministerio de Educación, Ciencia y Tecnología de la República Argentina, Buenos Aires, 2005. En: http://www.me.gov.ar/curriform/publica/nap/nap_egb2.pdf Solucionario Capítulo 1 1) Los números que faltan son: •En el cuadro 1. Fila 1: 1.004, 1.005, 1.008. Fila 2: 1.011, 1.016, 1.017, 1.019. Fila 3: 1.022, 1.023, 1.028. •En el cuadro 2. Fila 1: 1.040, 1.050, 1.080. Fila 2: 1.160, 1.170, 1.190. Fila 3: 1.200, 1.230, 1.280, 1.290. Fila 4: 1.310, 1.340, 1.370. •En el cuadro 3. Fila 1: 0. Fila 2: 1.200, 1.700, 1.900. Fila 3: 2.300, 2.600. Fila 4: 3.100, 3.400. Fila 5: 4.500, 4.800. Fila 6: 5.200, 5.600. Fila 7: 6.500, 6.700. Fila 8: 7.300, 7.800. Fila 9: 8.900. Fila 10: 9.100, 9.400. 2) En el Cuadro 1 avanzan de a 1 por fila y de a 10 por columna. En el Cuadro 2 avanzan de a 10 por fila y de a 100 por columna. En el Cuadro 3 avanzan de a 100 por fila y de a 1.000 por columna. 3) Los intrusos son los ubicados en las celdas sombreadas. Entre paréntesis, se encuentra el número correcto. 200 201 202 203 204 205 206 208 (207) 210 211 212 213 214 215 216 220 221 221 (222) 223 225 (224) 226 (225) 230 231 232 233 234 235 230 (240) 250 260 241 241 (251) 261 208 209 217 217 (218) 219 226 227 228 229 237 (236) 237 238 239 245 246 247 248 248 (249) 257 258 259 242 243 244 252 253 254 255 256 264 264 (265) 266 267 268 269 278 279 263 (262) 263 270 271 272 273 274 275 276 280 281 282 284 285 286 287 288 299 (290) 273 (283) 267 (277) 299 (289) 291 292 293 294 295 296 297 298 299 300 5) Siete mil quinientos cincuenta Mil doscientos treinta y cuatro Tres mil novecientos nueve Siete mil cincuenta y cinco Tres mil noventa y nueve Mil treinta y cuatro Siete mil quinientos cinco 1.234 7.055 7.505 7.550 3.909 3.099 1.034 6) En el Cuadro 1 van pintados los números 1.014 y 1.021. En el Cuadro 2 van pintados los números 1.240 y 1.350. a) 1.350. b) 1.240. c) 1.014. d) 1.021. Juego 4 0 0 2 3 0 0 0 3 2 0 8 1 2 1 1 7 1 4 1 0 0 0 1 0 1 4 3 6 3 0 1 9 0 0 0 2 4 1 2 0 2 3 0 0 8 0 1 0 1 0 9 1 0 0 0 6 1 1 0 7 9 8 5 8 0 0 1 2 0 0 0 5 5 0 0 9 0 6 8 0 7) a) 5.299 - 5.099. El menor es 5.099. b) 1.059 - 1.060. El menor es 1.059. c) 8.276 - 7.276. El menor es 7.276. d) 4.532 - 4.533. El menor es 4.532. 8) Hay varias respuestas posibles en cada caso. a) Por ejemplo, 3.047. b) Por ejemplo, 2.892. c) Por ejemplo, 1.099. d) Por ejemplo, 7.101. 9) Una de las muchas respuestas posibles es: a) 9.000 9.687 9.700 b) 7.050 7.129 7.200 c) 2.000 3.000 4.000 d) 5.079 5.080 5.085 10)3.000 - 3.003 - 3.030 - 3.300 - 3.309 - 3.333 - 3.390 - 3.903 3.930. 4) 4.200 4.210 4.220 4.230 4.240 4.250 4.260 4.270 4.280 4.290 4.300 4.201 4.211 4.221 4.231 4.241 4.251 4.261 4.271 4.281 4.291 4.202 4.212 4.222 4.232 4.242 4.252 4.262 4.272 4.282 4.292 4.203 4.213 4.223 4.233 4.243 4.253 4.263 4.273 4.283 4.293 4.204 4.214 4.224 4.234 4.244 4.254 4.264 4.274 4.284 4.294 4.205 4.215 4.225 4.235 4.245 4.255 4.265 4.275 4.285 4.295 4.206 4.216 4.226 4.236 4.246 4.256 4.266 4.276 4.286 4.296 4.207 4.217 4.227 4.237 4.247 4.257 4.267 4.277 4.287 4.297 4.208 4.218 4.228 4.238 4.248 4.258 4.268 4.278 4.288 4.298 4.209 4.219 4.229 4.239 4.249 4.259 4.269 4.279 4.289 4.299 Para conversar juntos •En el primer casillero, corresponde colocar el cero. Para darse cuenta hay que fijarse de qué manera aumentan los números. En este caso, en la fila, lo hacen de 100 en 100. Entonces, el número que falta es el cero. •Una forma de detectar los intrusos es mirar cómo “avanzan” los números en la fila o en la columna. •Para transformar el cuadro de los números del 200 al 300 en el de los números del 4.200 al 4.300, hay que agregar, delante de cada número, el número 4. Desafío 1.444 y 2.444. Hay 10 números: 1.204, 1.214, 1.224, 1.234, 1.244, 1.254, 1.264, 1.274, 1.284, 1.294. 11)a) $ 37. b) No le alcanza para comprar otra chalina. Le falta $ 1. c) Gastó $ 368. Pagó con $ 400. d) Sí, le alcanza. Gastaría $ 326. e) $ 370. f) Las posibilidades son las siguientes: Sacón (S), vestido (V) y chalina (CH): $ 490 - S, Remera (R) y Remera: $ 435 - S, R y CH: $ 418 - S, CH y CH: $ 401 - V, V y V: $ 381 - V, V y R: $ 309 - V, V y CH: $ 292 - V, R y R: $ 237 - V, R y CH: $ 220 - R, CH, CH: $ 131 - V, CH y CH: $ 203 - R, R y R: $ 165 - R, R y CH: $ 148 - CH, CH y CH: $ 114. 12)Producción personal. Desafío 40 90 20 30 50 70 80 10 60 Los conocedores 25 13) 25)Producción personal. 600 + 200 = 800 800 – 200 = 600 800 – 600 = 200 6.000 + 2.000 = 8.000 400 + 300 = 700 700 – 400 = 300 700 – 300 = 400 4.000 + 3.000 = 7.000 14)a) 1.205. b) 2.899. c) 2.300. d) 2.250. e) 977. f) 2.500. 26)Una posibilidad es: “Tracen un segmento AB que mida 5 cm. Apoyen la escuadra de manera tal que el vértice del ángulo recto coincida con el extremo A, y tracen el segmento AD que mida 3 cm. Apoyen la escuadra de manera tal que el vértice del ángulo recto coincida con el extremo D y tracen el segmento DC que mida 5 cm (AD debe quedar con la misma orientación que AB). Unan los extremos B y C”. 15)1.977 – 1.000 y 3.500 – 1.000. 27)Producción personal. 16)a) 7.000. b) 8.180. c) 5.666. d) 1.888. e) 2.345. f) 3.900. 28) 17)888 + 1.000, 1.345 + 1.000 y 2.900 + 1.000. 18)a) 4.200. b) 7.200. c) 10.400. Con la calculadora Cálculo 678 + 100 3.333 + 10 9.876 – 749 2.001 + 500 6.773 – 918 190 + 200 850 – 100 5.149 – 2.502 Con calculadora Uno menos 8.576 9.989 1.999 4.000 Número 8.577 9.990 2.000 4.001 Uno más 8.578 9.991 2.001 4.002 Número 1.237 2.039 3.100 5.999 entre 1.238 2.040 3.101 6.000 Número 1.239 2.041 3.102 6.001 Mentalmente 778 3.343 9.127 2.501 5.855 390 750 2.647 19)Primera fila, de izquierda a derecha: •“Es un rectángulo que tiene trazada una diagonal”. •“Es un hexágono”. •“Es un rombo propiamente dicho”. •“Es un rectángulo”. Segunda fila, de izquierda a derecha: •“Es un paralelogramo propiamente dicho”. •“Es un rombo que tiene trazada una diagonal”. •“Es un triángulo isósceles”. •“Es un trapecio”. Tercera fila, de izquierda a derecha: •“Es un cuadrado”. •“Es una circunferencia con dos diámetros trazados”. •“Es un triángulo rectángulo”. •“Es una circunferencia”. •“Es un cuadrado que tiene trazadas sus dos diagonales”. 29)2.332. 30)1.199, 1.100, 1.099, 1.010, 1.009, 1.001, 1.000. 31)6.901: entre 6.899 y 7.015. 5.038: entre 5.010 y 5.085. 32)7.256: Siete mil doscientos cincuenta y seis. 5.055: Cinco mil cincuenta y cinco. 9.999: Nueve mil novecientos noventa y nueve. 1.001: Mil uno. 33)a) Fueron 1.677 personas. b) Había más gente grande que chicos en edad escolar. c) No asistieron dos familiares por alumno. d) Para igualar el número de alumnos, tendrían que haber asistido 350 vecinos. 34)a) Se prestaron 371 libros en total. b) En la biblioteca quedaron 189 libros de Historia y 285 de Geografía. 35)Tiene 140 estampillas de Paraguay. 20)a) Cuadrado. Tiene 4 vértices, 4 lados y se pueden trazar dos diagonales. b) Paralelogramo. Tiene 4 vértices, 4 lados y se pueden trazar dos diagonales. c) Rombo. Tiene 4 vértices, 4 lados y se pueden trazar dos diagonales. d) Pentágono. Tiene 5 vértices, 5 lados y se pueden trazar 5 diagonales. e) Trapecio. Tiene 4 vértices, 4 lados y se pueden trazar dos diagonales. f) Triángulo. Tiene 3 vértices, 3 lados y no tiene diagonales. 21)Una posibilidad es: “Dibujá un cuadrado de 2 cm de lado y trazá sus diagonales”. Desafío Hay 9 rectángulos y 16 triángulos. 22)Producción personal. 23)Es necesario utilizar la escuadra en el último dibujo, porque no están marcados los “cuadraditos” que permiten trazar los segmentos perpendiculares. 24)Queda dibujado un cuadrado de 5 cm de lado. 26 Los conocedores 36)a) Bianca antes tenía $ 103. b) Entre la tía y la abuela le regalaron $ 94. 37) 500 + 100 = 600 600 – 500 = 100 600 – 100 = 500 5.000 + 1.000 = 6.000 300 + 500 = 800 800 – 500 = 300 800 – 300 = 500 3.000 + 5.000 = 8.000 700 + 200 = 900 900 – 700 = 200 900 – 200 = 700 7.000 + 2.000 = 9.000 38)a) 3.120. b) 1.499. c) 5.370. d) 4.500. e) 4.570. f) 4.573. g) 2.628. h) 3.541. i) 5.872. j) 1.300. k) 847. l) 3.962. 39)Joaquín puede elegir los cuadrados o el rombo propiamente dicho. Para conversar juntos •385 = 3 × 100 + 8 × 10 + 5 × 1. •65.652 = 6 × 10.000 + 5 × 1.000 + 6 × 100 + 5 × 10 + 2 × 1. 40)Producción personal. Desafío Hay 77 centenas. Hay 888 decenas. Hay 2.222 unidades. Hay 99 centenas, 999 decenas y 9.999 unidades. Capítulo 2 1) 1.832 1.530 2.460 1.220 1.600 3.250 + 40 + 70 + 50 + 300 + 400 + 2000 1.872 1.600 2.510 1.520 2.000 5.250 1.832 1.832 1.832 1.832 1.832 1.832 – 20 – 30 – 40 – 100 – 300 – 900 1.812 1.802 1.792 1.732 1.532 932 10)Podrán armar 126 bolsas de 10 jabones cada una. Les sobrarán 3 jabones. 11)Necesitaron 54 cajas. Debieron armar 540 bolsas de 10 jaboncitos cada una. No les sobraron jaboncitos. 12)Podrán armar 374 bolsas de 10 jaboncitos cada una, 37 cajas de 100 jaboncitos y 3 paquetes de 1.000. 2) 825 + 10 990 + 10 764 + 30 1.330 + 100 1.450 + 100 3.120 + 1.000 3.290 + 2.000 666 + 8.000 835 1.000 794 1.430 1.550 4.120 5.290 8.666 875 – 10 990 – 20 714 – 10 1.330 – 100 1.450 – 300 3.220 – 200 6.290 – 5.000 5.100 – 5.000 865 970 704 1.230 1.150 3.020 1.290 100 Con la calculadora • Sumar 2.000. • Hay más de una posibilidad. Se le puede sumar, por ejemplo, 100, 200, 300 o restarle 100 o 200. • Restarle 50. • Una posibilidad es: 0 + 9.000 + 800 + 70 + 6. • Una posibilidad es: 2.345 – 2.000 – 300 – 40 – 5. 13)Los cálculos que sirven son el b y el c. Para conversar juntos •Una explicación posible es: “Aunque intervengan las mismas cifras, los números formados no tienen el mismo valor. El valor de cada cifra depende del lugar que ocupa”. 3) No, porque hay que considerar la cantidad de decenas que hay en las unidades superiores. 4) Hay 52 decenas, 521 unidades y 5 centenas. 5) El lugar de las decenas lo ocupa el 2. El de las unidades, el 1. El de las centenas, el 5. 6) En el número… 1.537 5.371 7.135 3.751 1.753 el 5 vale… 500 5.000 5 50 50 el 3 vale… 30 300 30 3.000 3 el 7 vale… 7 70 7.000 700 700 el 1 vale… 1.000 1 100 1 1.000 14)Los cálculos que sirven son el b y el d. 15)Finalizó con 245 puntos. Se puede hacer 130 + 130 – 15 o 130 – 15 + 130. 16)Por ejemplo: Sofía es coleccionista de piedras, tiene 600 ejemplares de diversas clases. La semana pasada salió de excursión y encontró 58 nuevas piedras para agregar a su colección. Sin embargo, se le perdieron 20 en el camino. ¿Cuántas piedras tiene en total la colección de Sofía? 17)a) El Verde. b) El Azul. c) 1.° Rojo con 110 puntos. 2.° Verde con 100 puntos. 3.° Azul con 90 puntos. d) Obtuvo 30 puntos más. e) Obtuvo 100 puntos menos. 18) 1° 2° 3° Equipo Rojo Amarillo Azul Puntaje 27 24 12 7) 789, 798, 879, 897, 978 y 987. 19)a) 9.532. b) 8.923. c) 5.647. d) 21.865. 8) En el número… el 9 vale… 9.687 900 (9.000) 6.978 900 8.769 9 el 8 vale… 80 8 8.000 el 7 vale… 70 (7) 70 7.000 (700) el 6 vale… 600 600 (6.000) 60 20)a) 3.000 + 900 + 80 + 5. b) 7.000 + 200 + 40 + 4. c) 2.000 + 900 + 80 + 6. 21)a) 20.000. b) 28.000. c) 28.700. d) 30.000. e) 34.000. f) 34.500. 9) Billetes $ 10.000 $ 1.000 $ 100 18 pantalones $ 2.754 0 2 7 10 vestidos $ 12.350 1 2 3 11 chalinas $ 385 0 0 3 8 trajes $ 4.080 0 4 0 Prenda Valor $ 10 5 5 8 8 $1 4 0 5 0 22)a) 50.000 + 6.000 + 400 + 90 + 7 = 56.497. b) 90.000 + 2.000 + 500 + 60 + 3 = 92.563. c) 20.000 + 5.000 + 800 + 40 + 9 = 25.849. Desafío Hay varias respuestas. Por ejemplo, 896 – 823 o 901 – 828. Los conocedores 27 31)Producción personal. 32)Hay dos soluciones posibles: 23) Menor que 1.000 510 + 507 × × 615 + 122 × 550 + 440 × ambos números son menores que 500. ambos números son mayores que 500. 500 supera en más de 300 unidades a 122 y 615 solo en 115 a 500. los 50 de 550 no alcanzan para compensar los 40 de 440 para obtener 1.000. 3c m 5 cm 5 cm 33)a) 9.320. b) 2.039. 34)Hay varias soluciones posibles. Por ejemplo, 21.395, 19.472, 76.951, 92.357 y 38.459. 24) Mayor que Menor que Me di cuenta porque... 10.000 10.000 5.000 + 6.000 = 11.000 y 5.100 + 6.700 × es mayor que 10.000. ambos números son 4.999 + 4.888 × menores que 5.000 los 200 de 5.200 no llegan a compensar los 700 4.700 + 5.200 × de 4.700 para obtener 10.000. 700 + 300 = 1.000 y 4.000 4.700 + 6.300 × + 6.000 = 10.000. 25)a) 14.000. b) 70.000. 26)Producción personal. 27)Dibujá un ángulo de 30° cuyos lados midan 3 cm. Dibujá un segmento de 7 cm con uno de los extremos que coincida con el extremo del segmento de 3 cm que no coincide con el vértice del ángulo de 30°. Ambos segmentos deben formar un ángulo de 65°. En el otro extremo del segmento de 7 cm, en sentido contrario al segmento de 3 cm, dibujá un segmento de 3 cm, que forme un ángulo de 90° con este. Para conversar juntos •No se puede copiar el dibujo usando solamente la escuadra. Es necesario usar transportador o compás para reproducir los ángulos diferentes de 90°. 28)Solo el 2.° ángulo es menor que 90°. Para poder dar la respuesta podemos utilizar la escuadra. Desafío Hay 8 ángulos de cada tipo. 29)Los ángulos miden, aproximadamente, 110°, 40° y 130°. Si utilizo el transportador, encuentro que la medida es: 100°, 50° y 125°, respectivamente. 30)Producción personal. Para conversar juntos •Un ángulo recto mide 90°. 28 4 cm m 4c 478 + 499 Me di cuenta porque... 3 cm Mayor que 1.000 Los conocedores 35)a) 4.322 = 4 × 1.000 + 3 × 100 + 2 × 10 + 2. b) 87.654 = 8 × 10.000 + 7 × 1.000 + 6 × 100 + 5 × 10 + 4. 36)V, V, F. 37)1.450, 1.490, 1.620, 1.400, 1.220, 1.720 y 16.200. 38)a) 20.765. b) 30.598. c) 28.065. d) 34.098. e) 28.705. f) 34.508. g) 28.760. h) 34.590. 39)• María Laura compró 3 camisas por las que pagó $ 150 en total y un pantalón que le costó $ 72. ¿Cuánto dinero gastó en toda la compra? • Enzo compró 5 kg de papas y 2 kg de batatas. Si cocinó 1 kg de papas y 1 kg de batatas, ¿cuántos kilos de papas y batatas le quedan aún en total? 40)a) 1.900. b) 10.000. c) 10.650. 41)a) 17.000. b) 30.096. c) 34.048. d) 80.000. e) 40.943. 42)a) 3.247 = 3.000 + 200 + 40 + 7. b) 32.478 = 30.000 + 2.000 + 400 + 70 + 8. 43)a) 1.389. b) 55.555. c) 1.235. d) 8.042. e) 12.007. 44)Producción personal. 45)• Dibujá 12 segmentos que forman una poligonal cerrada no cruzada. Son todos perpendiculares entre sí y miden 1 cm, 2 cm, 1 cm, 1 cm, 2 cm, 1 cm, 1 cm, 2 cm, 1 cm, 1 cm, 2 cm y 1 cm, respectivamente. • Dibujá un triángulo isósceles cuyos lados iguales midan 4 cm y el lado desigual 3 cm. • Dibujá un ángulo de 140° cuyos lados midan 3 cm y 3,5 cm. Trazá un segmento de 6 cm que tenga un extremo que coincida con el extremo diferente del vértice del ángulo de 140° del segmento de 3 cm y que forme con este segmento un ángulo de 15°. El segmento de 6 cm cruza al segmento de 3,5 cm. • Dibujá 4 segmentos consecutivos que midan 2 cm; 2,5 cm; 4 cm y 2,5 cm. El de 2 cm debe formar un ángulo de 60° con el de 2,5 cm; este último debe formar un ángulo de 30° con el de 4 cm y no cruza al de 2 cm; y el de 4 cm debe formar un ángulo de 90° con el de 2,5 cm. Los segmentos que miden 2,5 cm deben quedar en lados contrarios respecto del segmento de 4 cm. 46)Producción personal. Capítulo 3 1) X vale 10. I vale 1. 2) I = 1; V = 5; X = 10; C = 100; L: 50; X: 10. 7 = VII; 12 = XII; 21 = XXI; 43 = XLIII; 108 = CVIII; 134 = CXXXIV. Para conversar juntos •3 = III; 4 = IV; 22 = XXII; 40 = XL; 6 = VI; 60 = LX. •Algunas inferencias posibles son: “Los símbolos escritos a la derecha de otro le suman su valor” y “I y X a la izquierda restan valor”. 3) Las escrituras incorrectas son: XXXXI, VC, CCM, IC, XXXIIII y XM. Para conversar juntos •El sistema de numeración romano no es un buen sistema para calcular porque no es posicional como el sistema de numeración decimal. La diferencia principal es que el sistema romano es aditivo y el nuestro, multiplicativo, decimal y posicional. 4) a) Puede elegir entre 18 peluches diferentes (6 × 3). b) Cocinó 24 masitas (6 × 4). c) Habrían tenido que tocar hasta 48 timbres (12 × 4). 5) a) Gastó $ 120 y compró 144 pañales. Datos no necesarios: piso 9 y departamento 3. b) Puede hacer 48 combinaciones para vestirlo. Datos no necesarios: 15 días y 18 de abril. c) Hay 48 personas. Dato no necesario: Parrilla 78. d) Se sirven 25 ravioles en cada plato. Don Lucio prepara 750 ravioles por día. Datos no necesarios: Parrilla 78, 52 años. 6) Sí, está bien. 7) 50, 500, 5.000, 120, 230, 670, 1.230, 44.560 y 7.890. 8) Se necesitan 30, 300 y 3.000 agujas para armar 3, 30 y 300 sobrecitos. Se necesitan 400, 4.000 y 40.000 agujas para armar 4, 40 y 400 paquetes. Se necesitan 6.000, 60.000 y 600.000 agujas para armar 6, 60 y 600 cajas. •Las cuentas de Abril y de Agustín representan cálculos algorítmicos de la multiplicación, mientras que las cuentas de Lucía y de Joaquín representan cálculos mentales. •En la cuenta de Abril, el 1 que está arriba del 2 indica que se debe sumar otra decena al 20 × 2. •En la cuenta de Agustín el 1 está en el 16. 15)a) Puede dividir por 2. b) 18 × 2 × 100. c) a) 500 × 2 × 2. b) 500 × 200 × 2. c) 2 × 2 × 21. d) 200 × 2 × 21. e) 500 × 2 × 20. f) 230 × 2 × 22. g) 2 × 20 × 21. h) 2 × 22 × 21. d) a) 37 × 4. b) 37 × 8. c) 46 × 9. d) 46 × 27. e) 23 × 16. f) 12 × 25. e) 35 × 1.000 = 35.000. Para conversar juntos • 25. • Si a un número cualquiera lo multiplicamos y lo dividimos por el mismo número, obtenemos el número inicial, ya que estamos multiplicando por 1. 16)Por ejemplo: B E G A 3 cm H F D C Para conversar juntos •Para marcar los puntos podemos trazar la circunferencia de radio 3 cm, utilizando el compás. •Los puntos que están sobre la circunferencia se encuentran a 3 cm de A, los que están en el interior del círculo, a menos de 3 cm de A, y los que están en el exterior del círculo, a más de 3 cm de A. Para conversar juntos •La medida del diámetro de la circunferencia es equivalente a dos veces la medida del radio (d = 2r). 9) a) 3.200. b) 45.000. 17)Producción personal. Desafío 40 × 10 = 4 × 100. 50 × 100 = 5 × 1.000. 230 × 10 = 23 × 100. Para conversar juntos •Se utiliza regla y compás. Se puede comenzar trazando el segmento y luego las tres circunferencias que tienen ese segmento o parte de él como diámetro. 10)a) 500. b) 1.000. c) 750. 18)Producción personal. 11)a) 420. b) 630. c) 840. 12)a) 80 × 2 = 160 b) 60 × 9 = 540 c) 900 × 4 = 3.600 (8 × 2 = 16) (6 × 9 = 54) (9 × 4 = 36) Para conversar juntos •Para hacer el dibujo se necesita regla y compás. Para tomar medidas se puede utilizar el compás. Desafío 13)a) 40 × 5 = 200 400 × 5 = 2.000 4.000 × 5 = 20.000 b) 80 × 9 = 720 800 × 9 = 7.200 8.000 × 9 = 72.000 14)336 plantines. Para conversar juntos Los conocedores 29 19)Producción personal. 25)a) 222. b) 555. c) 1.111. d) 2.002. e) 70. f) 98. g) 43. h) 444. Para conversar juntos •Para tomar las medidas se utiliza el compás. •Para copiar los segmentos, primero trazamos con la regla no graduada un segmento cualquiera, luego medimos con el compás la longitud de uno de los segmentos de la figura dada y la trasladamos sobre el segmento trazado inicialmente. A continuación apoyamos el compás en uno de los extremos del segmento de la figura y tomamos la medida hasta la intersección de los dos segmentos. Esta medida representa la mitad de cualquiera de los segmentos de la figura. Trasladamos esta medida al segmento que representa la copia y marcamos el punto medio. Dibujamos el otro segmento que es perpendicular al anterior y lo corta en su punto medio. 26)a) MD. b) CL. c) V. d) MMMCC. e) CCCXX. f) XXXII. 27)Por ejemplo: 827 → DCCCXXVII 379 → CCCLXXIX 28)70 = LXX. 99 = XCIX. 29)a) VIII. b) DCCCLXXXVIII. c) LXXXVIII. d) VIII DCCCLXXXVIII. 30)Cristina y Jorge tenían 20 opciones posibles para cenar. 20)Se puede tomar la medida de un segmento comparando la abertura del compás con la longitud del segmento. 31)101. La solución depende de cómo se parta la figura para poder contar los rectangulitos. Las soluciones correctas son: 11 × 4 + 7 × 3 + 9 × 4; 4 × 4 + 4 × 4 + 5 × 11 + 7 × 2; 4 × 4 + 9 × 4 + 7 × 7; y 4 x 4 x 2 + 5 x 11 + 7 x 2. 21)Producción personal. 32)En las bandejas acomodaron 240 alfajores. Para conversar juntos •Pueden encontrar un instructivo para copiar ángulos con regla y compás en el capítulo 5, página 85. 33)5 cuadernos costarán $ 100. 22) 2 cm 4 cm 2 cm 34)17 × 10 17 × 100 17 × 1.000 170 × 10 170 × 100 170 × 1.000 1.700 17.000 170 17.000 1.700 170.000 35)58 × 10 = 580. 43 × 100 = 4.300. 100 × 92 = 9.200. 1.000 × 25 = 25.000. 36)Por ejemplo, Para conversar juntos •Todas las construcciones deberían ser las mismas porque se indican las medidas. 48 × 10 2.600 130 × 20 710 71 × 10 2.800 28 × 100 1.000 37)Producción personal. 38) B cm A 2 A 2 cm de B 4 cm 23)Por ejemplo: “Trazá un segmento de 4 cm. Con centro en el punto medio del segmento, trazá una circunferencia de radio 2 cm. Con centro en el mismo punto, trazá una circunferencia de radio 1 cm.” Para conversar juntos •En general escribirán mensajes similares, porque otra posibilidad significaría pensar en circunferencias concéntricas y luego trazar el diámetro de la circunferencia de radio mayor. A más de 2 cm de B C 24) P D 39)Producción personal. 40) A E Para conversar juntos •Si unen los centros de las circunferencias, se forma una circunferencia con el mismo radio que el de las circunferencias dibujadas. 30 Los conocedores G B C 41)Producción personal. 4 cm D F Capítulo 4 b)90 : 10 = 9 d)7.000 : 10 = 700 f)4.500 : 10 = 450 900 : 10 = 90 7.000 : 100 = 70 2.700 : 10 = 270 9.000 : 10 = 900 7.000 : 1.000 = 7 6.800 : 100 = 68 1) 0 km 10 km 20 km 30 km 40 km 2) 0 km 100 km 200 km 3) 0 km 500 km 1.000 km 1.500 km 2.000 km Para conversar juntos •Cuando dividimos por 100 un número que termina por lo menos con 2 ceros, le quitamos los últimos 2 ceros. Cuando dividimos por 1.000 un número que termina por lo menos en 3 ceros, le quitamos los últimos 3 ceros. Para conversar juntos •Las cuentas de Paula y Ángela se parecen en que, en ambas, 621 se desarma en 500 + 100 + 20 + 1. Las de Ignacio y Ángela se parecen en que ambos resuelven el cálculo por medio del algoritmo no convencional de la división, “reparten” por partes. Además, las cuentas de Ignacio y Ángela se diferencian en que el procedimiento de Ángela es más económico. 4) 10)a) 407 : 4 está cerca de 100. b) 5.120 : 5 está cerca de 1.000. c) 31 : 3 está cerca de 10. 0 km 1.000 km 2.000 km 3.000 km 4.000 km 5.000 km 5) a) Tiene 40 plantines de petunias para ubicar en cada hilera (240 : 6). En cada hilera irían 20 plantines de color violeta, 12 de color rosa y 8 de color blanco (120 : 6, 72 : 6 y 48 : 6). b) Gastó $ 368 (2 × 49 + 5 × 20 + 20 × 4 + 30 × 3). Para pagar usó 4 billetes. De vuelto le dieron $ 32 (400 – 368). c) Mariano tuvo que cargar 22 cajas (198 : 9). Para conversar juntos •Para resolver estos problemas se utilizan todas las operaciones, pero especialmente la multiplicación y la división. Los cálculos realizados están explicitados anteriormente. •Hay más de una manera de resolverlos. Por ejemplo en el inciso e, en lugar de plantear la división, los chicos pueden probar con diferentes multiplicaciones hasta obtener el número que, multiplicado por 9, da 198. 6) 8 × 5 = 40 40 : 5 = 8 40 : 8 = 5 9 × 7 = 63 63 : 7 = 9 63 : 9 = 7 8 × 9 = 72 72 : 8 = 9 72 : 9 = 8 4 × 6 = 24 24 : 4 = 6 24 : 6 = 4 7) 3 × 9 = 27 27 : 3 = 9 27 : 9 = 3 Desafío Multiplicar 60 × 8 es equivalente a multiplicar 80 × 6, porque 60 × 8 = 6 × 10 × 8 = 6 × 80 = 80 × 6. 200 × 4 = 2 × 400 y 250 × 2 = 25 × 20. Si 30 × 9 = 270, entonces 270 : 3 = 90. 8) a) 12. b) 120. c) 1.200. Para conversar juntos •Como en todos los casos dividimos por un número de una sola cifra, para decidir por cuál potencia de 10 elegir, basta con tener en cuenta el tamaño del dividendo. 11)a) Podría dividir por 10. b) Podría haber dividido por 100. 47.200 : 100 = 472. c) Podría haber dividido por 1.000. 99.000 : 1.000 = 99. d) Podría dividir dos veces por 2. 12)a) 24 × 7 = 168. b) 360 : 60 = 6. c) 152 : 19 = 8. d) 29 × 11 = 319. e) 77 × 5 = 385. f) 400 : 8 = 50. 13)¿Tiene dos lados iguales? ¿Es obtusángulo? Para conversar juntos a) ¿Tiene un ángulo recto? ¿Tiene sus tres lados desiguales? ¿Tiene un lado que mida más de 5 cm? b) ¿Tiene dos lados iguales? ¿Es obtusángulo? c) ¿Tiene un ángulo recto? ¿Tiene dos lados iguales? d) ¿Tiene sus tres lados desiguales? ¿Tiene un ángulo obtuso? ¿Tiene un lado que mida más de 7 cm? e) ¿Tiene sus tres ángulos agudos? ¿Tiene dos lados iguales y uno desigual? f) ¿Tiene sus tres lados iguales? g) ¿Tiene sus tres lados desiguales? ¿Tiene tres ángulos agudos? h) ¿Tiene un ángulo recto? ¿Tiene sus tres lados desiguales? ¿Tiene un lado que mida más de 5 cm? i) ¿Tiene sus tres lados desiguales? ¿Tiene un ángulo obtuso? ¿Tiene un lado que mida más de 7 cm? •Ana eligió el triángulo b. 14)El triángulo que adivinó Leo es el e. 15)No es suficiente. Es necesario indicar si es rectángulo o acutángulo. Para conversar juntos •Uno de los chicos desarma 240 en 200 + 40, y divide cada sumando por 2. El otro sabe que 24 : 2 es 12, entonces si le agrega un 0 a 24, deberá agregarle un 0 al resultado, a 12. 16)a) Es rectángulo y escaleno. Uno de sus lados mide 4 cm. b) Es obtusángulo e isósceles. c) Es rectángulo e isósceles. 9)a)68 : 2 = 34c)80 : 4 = 20e)35 : 5 = 7 680 : 2 = 340 800 : 4 = 200 350 : 5 = 70 6.800 : 2 = 3.400 8.000 : 4 = 2.000 3.500 : 5 = 700 18)Un triángulo rectángulo no puede ser equilátero. En el equilátero todos los ángulos miden 60°. 17)Fede eligió el triángulo b. Los conocedores 31 19)Es un triángulo rectángulo y escaleno. Los lados del ángulo recto miden 2,5 cm y 8,5 cm, aproximadamente. Para conversar juntos •Muchos chicos posiblemente no tengan en cuenta las medidas del triángulo. 33)450 : 90 = 5. 7.200 : 90 = 80. 7.200 : 900 = 8. 34)a) 16 × 15 = 240. b) 55 × 11 = 605. c) 39 × 12 = 468. d) 168 : 24 = 7. e) 660 : 110 = 6. f) 800 : 20 = 40. 35)Por ejemplo: 20)Producción personal. Para conversar juntos •No todos dibujarán los mismos triángulos, porque tendrán diferentes medidas los lados y ángulos. Además, algunos dibujarán, en el caso del triángulo isósceles, triángulos isósceles acutángulos, otros isósceles rectángulos y otros isósceles obtusángulos. Y en el caso del triángulo acutángulo, algunos dibujarán acutángulos isósceles, otros acutángulos escalenos y otros acutángulos equiláteros. Desafío Se dibujan 9 triángulos. 21)a) 4.203 < 4.230. b) 9.777 > 9.767. c) 5.998 < 6.000. d) 3.654 < 3.821. a) b) d) c) e) a) Escaleno y obtusángulo. b) Escaleno y rectángulo. c) Equilátero y acutángulo. d) Isósceles y rectángulo. e) Isósceles y acutángulo. 22)807 - 870 -1.008 - 1.080 - 1.800 - 2.543 - 2.601 - 2.610. 36)a) c. b) b. 23)501 - 510 - 599 - 5.001 - 5.010 - 5.099 - 5.100. 24) Uno menos: el anterior 9.999 24.998 30.000 10.000 24.999 30.001 Uno más: el posterior 10.001 25.000 30.002 37)Nora pudo haber preguntado: ¿Es un triángulo rectángulo? Otras preguntas posibles pueden ser: ¿Es un triángulo equilátero? ¿Es un triángulo acutángulo? 38)a) Obtusángulo y escaleno. b) Rectángulo y escaleno. c) Rectángulo y escaleno. Capítulo 5 25)Los números que faltan son: 50, 150 y 250. 1) 26) 0 20 15 238 quince mil doscientos treinta y ocho 88.888 ochenta y ocho mil ochocientos ochenta y ocho 40 27)a) Tiene que llevar $ 189. b) Cada uno tiene que poner $ 63. 28)Les conviene viajar en auto, ya que gastarían $ 600, mientras que en micro gastarían $ 720. 29)A cada puesto le tocaron 23 globos. 30)En cada bolsita colocó 4 chupetines. No alcanzaron. Si quiere poner 3 dados en cada bolsita necesita 90 dados. 31)a) 8. b) 16. c) 12. d) 24. e) 4. f) 2. 32)a) 60 : 10 = 6 d)5.000 : 10 = 500 600 : 10 = 60 5.000 : 100 = 50 6.000 : 10 = 600 5.000 : 1.000 = 5 b) 350 : 10 = 35 e)3.200 : 100 = 32 3.400 : 10 = 340 6.800 : 100 = 68 8.200 : 10 = 820 7.600 : 100 = 76 c) 49 : 7 = 7 f)56 : 8 = 7 490 : 7 = 70 560 : 8 = 70 4.900 : 7 = 700 5.600 : 8 = 700 32 Los conocedores 10.000 + 5.000 + 200 1 decena de mil, 5 + 30 + 8 unidades de mil, 2 centenas, 3 decenas y 8 unidades 80.000 + 8.000 + 800 8 decenas de mil, 8 + 80 + 8 unidades de mil, 8 centenas, 8 decenas y 8 unidades 70.000 + 7.000 + 700 7 decenas de mil, 7 + 70 + 7 unidades de mil, 7 centenas, 7 decenas y 7 unidades 430.800 cuatrocientos 400.000 + 30.000 4 centenas de mil, 3 treinta mil + 800 decenas de mil y 8 ochocientos centenas 125.966 Ciento 100.000 + 20.000 + 1 centena de mil, 2 veinticinco mil 5.000 + 900 + 60 + 6 decenas de mil, 5 novecientos unidades de mil, 9 sesenta y seis centenas, 6 decenas y 6 unidades 77.777 setenta y siete mil setecientos setenta y siete 2) a) Son ofertas, porque cada ovillo de lana roja cuesta $ 9, si compro 3 pagaría $ 27; y cada ovillo de lana azul cuesta $ 12, si compro 4 pagaría $ 48. b) Ahorra $ 2 y $ 8, respectivamente. c) Puede comprar 8 bufandas. Si decide comprar una bufanda más, debe agregar $ 5. d) Para acomodar todos los ovillos necesita 8 canastos. En 7 canastos colocará 15 ovillos y en un canasto, 10 ovillos. e) Ovillos 3 6 9 12 15 18 21 24 27 30 rojos Precio $ 25 $ 50 $ 75 $ 100 $ 125 $ 150 $ 175 $ 200 $ 225 $ 250 Ovillos 4 8 12 16 20 24 28 32 36 40 azules Precio $ 40 $ 80 $ 120 $ 160 $ 200 $ 240 $ 280 $ 320 $ 360 $ 400 6) a) Armaron 26 hileras. b) 20 + 20 + 10 + 5 = 55. c) En la primera cuenta: 100 × 8 = 800, 20 × 8 = 160 y 4 × 8 = 32. En la segunda cuenta: 100 × 4 = 400, 100 × 4 = 400, 20 × 4 = 80, 20 × 4 = 80 y 7 × 4 = 28. 7) f) Puede armar: 1 paquete de 36 botones. 2 de 18. 3 de 12. 4 de 9. 6 de 6. 9 de 4. 12 de 3. 18 de 2. 36 de 1. Para conversar juntos •Para que haya una única respuesta, en el enunciado se debe incluir la cantidad de botones que se quiere colocar en cada paquete. g) Puede colocar en cada paquete 6 botones. Si quiere colocar 6 botones en cada paquete, puede armar 8 paquetes. ← Divisor Dividendo → 50 6 ← Cociente Resto → 2 8 ← Divisor ← Cociente Desafío Los números que faltan son: 0, 77 y 23, respectivamente. Con calculadora 11.816 5.400 45.711 1.100 300 1.544.892 Mentalmente 1.111 8.888 : 8 8.771 : 49 1.000 : 100 3.070 : 10 34.804 : 77 2.800 : 2 80.730 : 69 9.000 : 1.000 3) Dividendo → 50 8 Resto → 2 6 Mentalmente 64 9.000 8×2×2×2 90 × 100 2.954 × 2 × 2 540 × 10 5.079 × 3 × 3 100 × 11 25 × 12 90.876 × 17 Con calculadora 179 10 307 452 1.400 1.170 9 Para conversar juntos •Las cuentas de Analía y Ariel se parecen en que ambos resuelven el cálculo mediante el algoritmo no convencional de la división, “reparten” por partes. Se aproximan progresivamente al resultado con multiplicaciones por números redondos (utilizan estrategias de cálculo mental). Se diferencian en que el procedimiento de Analía es más económico que el de Ariel. •Las cuentas de Analía y Lautaro se parecen en que, en ambas, 587 se desarma. La diferencia está en que descomponen el número de diferente manera. Analía desarma de la siguiente manera: 500 + 50 + 37 y Lautaro así: 250 + 250 + 50 + 25 + 12. •Si Leda y Caro deciden armar un collar más necesitarán 13 botones. 9) 5) 555 : 23 = 24 (para resolver, los chicos pueden descomponer el resultado en 10 + 10 + 1 + 1 + 1 + 1). Un problema posible: En la escuela están organizando una fiesta. Hicieron una rifa para recaudar fondos. Los $ 555 que se recaudaron se repartirán entre los 23 cursos. ¿Cuánto dinero recibirá cada curso? ¿Cuánto dinero sobrará? 510 : 12 = 42 (los chicos, para resolver pueden descomponer el resultado en 20 + 20 + 2). Un problema posible: En la panadería prepararon 510 masitas de coco. Si quieren poner 12 en cada bandeja, ¿cuántas bandejas podrán armar? ¿Cuántas masitas sobran? 7 4 cm Para conversar juntos •Todos construyen el mismo triángulo porque se fijan 3 datos. •Los instrumentos geométricos que se utilizan son regla graduada y compás. •No es posible construir un triángulo cuyos lados midan 2 cm, 4 cm y 7 cm: la medida de cada lado debe ser menor que la suma de las medidas de los otros dos lados. 10) 6 cm Para conversar juntos •Las cuentas de Hernán y Magda se diferencian en que la de Magda es más económica y, además, en la estrategia de cálculo mental utilizada. Hernán hace lo siguiente: •449 = 10 × 14 + 10 × 14 + 10 × 14 + 1 × 14 + 1 × 14 + 1. Magda: 449 = 14 × 2 × 10 + 10 × 14 + 14 × 2 + 1. •La cuenta de Hernán se parece más a la de Ariel, y la de Magda, a la de Analía. 5 cm 8) Para que sea posible la reproducción de la figura debemos agregar las medidas de los lados del triángulo. cm 4) Podrán armar 23 collares de 25 botones cada uno. Les sobrarán 12 botones. 70º 5 cm Para conversar juntos •Todos construyen el mismo triángulo porque se fijan 3 datos. •Los instrumentos geométricos que se utilizan son regla graduada y transportador. •Si no se hubiera indicado la medida del ángulo, no habrían podido construir todos el mismo triángulo porque, por ejemplo, habría variado la medida del ángulo formado entre los lados. Los conocedores 33 11)Producción personal. 28)Se pueden dibujar diferentes triángulos porque necesito 3 datos para poder construir un único triángulo. 12)a) Para que las circunferencias se crucen la suma de las medidas de los dos radios debe superar los 9 cm. b) Las circunferencias no se cruzarán cuando la suma de las medidas de los dos radios sea inferior a 9 cm. c) Las circunferencias tendrán un punto en común cuando la suma de las medidas de los dos radios sea 9 cm. 13)Producción personal. 45º 5 cm 3 cm 14) 29) Se puede dibujar un único triángulo porque tengo tres datos. 5c m 15)8.701 8.710 8.071 80.710 80.071 80.701 6 ochenta mil setecientos uno 8.000 + 700 +1 8 decenas de mil, 7 decenas, 1 unidad 8 decenas de mil, 7 centenas, 1 decena ocho mil setenta y uno 8.000 + 700 + 10 16)a) 87.399 > 87.099. b) 25.001 < 25.010. c) 43.150 < 44.000. d) 62.086 < 62.088. cm m 5c 4 cm 7 cm 30)Por ejemplo, 9 cm, 12 cm y 17 cm. 31) Se puede dibujar un único triángulo porque tengo tres datos. 7c m 17)a) Por ejemplo, 19.034. b) Por ejemplo, 31.920. c) 51.290. d) Por ejemplo, 71.002. 18)20.001 - 20.010 - 20.100 - 200.001 - 200.010 - 200.100 210.000. 60º 19)Por los 193 jarros pagó $ 965. 5 cm 20)Con $ 125 se pueden comprar 8 cuadernos. Con $ 250 alcanza para comprar 16 cuadernos. 32)La solución no es única. Falta un dato para que lo sea. 21)En cada caja habrá 13 alfajores. 22)Por ejemplo: “Tengo 78 frascos de mermelada para acomodar en 5 estantes. Si quiero poner la misma cantidad de frascos en cada estante, ¿cuántos frascos acomodaré en cada uno? ¿Me sobrarán frascos?” 6 cm 23)Por ejemplo: “Tengo 169 cajas para llevar a un depósito. Si en cada viaje solo puedo trasladar 12 cajas, y debo trasladarlas todas, ¿cuántos viajes tengo que realizar?” 33)Se pueden dibujar diferentes triángulos. Por ejemplo: 24)En cada estante acomodaré 12 libros. No podré acomodar todos los libros (me sobran 4), porque en cada estante debo colocar la misma cantidad. 25)a) 100 × 25 = 2.500. 10 × 25 = 250. 1 × 25 = 25. Cociente: 111. b) 200 × 13 = 2.600. 20 × 13 = 260. 3 × 13 = 39. Cociente: 223. 26)a) 100 + 100 + 20 + 20 = 240. b) 100 + 20 + 20 + 2 = 142. 27)El triángulo es equilátero y acutángulo. 7 cm Los conocedores 34)Producción personal. Capítulo 6 60º 34 5 cm 1) a) Puede usar en cada torta 2 1/2 frascos. Se puede seguir repartiendo lo que sobra. b) A cada alumno le debe entregar 2 libros. No se puede seguir repartiendo lo que sobra: 5 libros. c) A cada persona le debe dar $ 37,25. Se puede seguir repartiendo. d) En cada florero tiene que colocar 5 flores. No se puede seguir repartiendo lo que sobra: 2 flores. e) A cada equipo le dará 3 hojas y 1/3 de hoja. Se puede seguir repartiendo. f) A cada uno le tocarán 2 alfajores y 2/5 de alfajor. Se puede seguir repartiendo. Para conversar juntos •En los casos en los que las cantidades son continuas se puede seguir repartiendo el resto; en los casos de cantidades discretas, no. 10)a) 10. b) 100. c) 1.000. d) 923 con resto 1. e) 92 con resto 31. f) 9 con resto 230. 11) Entre 1 y 10 Entre 10 y 100 Entre 100 y 1.000 18.300 : 2 × 455 : 5 75 : 8 Entre 1.000 y 10.000 × × 2.137 : 3 × 2) Por ejemplo, para el inciso e: Equipo 1 Equipo 2 Equipo 3 Para conversar juntos Las soluciones de Abril y Agustín se pueden escribir de la siguiente manera: 2 2/5. 3) Está pintada la mitad en los pinceles, el chocolate, los sacapuntas y el círculo. Para conversar juntos •Tanto Belén como Nahuel tienen razón. Belén tiene 1 de 3 caramelos de menta y Nahuel 2 de 6 caramelos. Ambas fracciones son equivalentes: 1/3 = 2/6. •Para darse cuenta de en qué casos está pintada la mitad, cuando las cantidades son discretas, contamos los objetos y observamos que la mitad estén pintados. Cuando las cantidades son continuas, nos fijamos si la figura está dividida en dos partes equivalentes y una de ellas está pintada. •La quinta parte con números fraccionarios se escribe 1/5. Desafío Son 4 amigos. 4) 1/3, 1/2 y 1/4, respectivamente. 5) 1/5, 1/4 y 1/3, respectivamente. 6) 1/5 y 1/4, respectivamente. Para conversar juntos •Dividir por 10, por 100 y por 1.000 significa sacarle al dividendo (contando desde las unidades) tantos ceros como tiene la potencia de 10 por la que divido. En el caso de que los números no terminen en tantos ceros como tiene la potencia de 10, significa sacarle tantos lugares (también contando desde el lugar de las unidades) como tiene la potencia de 10 por la que divido. Por ejemplo, al dividir 9.231 por 10, le saco el 1 y el resultado será 923 y el resto 1. Sucede que estoy descomponiendo a 9.231 en 9.230 + 1. •Para decidir en qué columna marcar, como en todos los casos se divide por un número de una cifra, se puede observar la magnitud del dividendo y luego la proximidad del divisor al 1 o al 10. Con la calculadora • Cociente 6 y resto 3. • Cociente 11 y resto 7. • Cociente 15 y resto 7. 12)Su compañero puede elegir las figuras: a, b, c, f, h, j, l, m, o. Para conversar juntos •Para poder identificar todos la misma figura, debemos dar otras indicaciones, por ejemplo, si tiene señalada una diagonal, o dos diagonales; si tiene ángulos rectos; etc. También se puede considerar el nombre de la figura. 13)Dos pistas posibles son: •Es un rectángulo propiamente dicho. •Tiene dos pares de lados, respectivamente iguales; y todos sus ángulos son rectos. En estas pistas no se considera, por ejemplo, la medida, porque se distingue el rectángulo h del l, que tiene señalada una diagonal. Si hubiera que tener en cuenta otras figuras (con otros rectángulos dibujados), posiblemente se deberían considerar otras pistas. 7) Van pintados cuatro soles y la mitad del cuadrado. 9) a) 93. b) 930. c) 9.300. d) 74. e) 740. f) 744. g) 45. h) 85. i) 63. 15)a) Por ejemplo: 4 cm 8) a) En la primera cuenta, Miranda hizo: 200 × 12 = 2.400, 30 × 12 = 360 y 4 × 12 = 48. En la segunda cuenta hizo: 400 × 11 = 4.400, 50 × 11 = 550 y 7 × 11 = 77. b) En la primera, considerando 40 y 4. En la segunda, considerando 200, 20 y 2. 14)Un cuadrado es un rectángulo porque es un paralelogramo y tiene sus ángulos rectos. 4 cm Para conversar juntos •Porque del total de objetos debo tener pintada la tercera parte. Al ser cantidades discretas, debo contar los objetos y dividirlos por 3. Esa cantidad obtenida luego de la división representa la tercera parte. Se pueden construir diferentes rectángulos con dos lados que miden 4 cm. Si se quiere dibujar un único cuadrilátero, hay que fijar la medida de los otros lados. Los conocedores 35 b) Por ejemplo: Para conversar juntos •Para construir un cuadrado se necesita la medida de los lados, y si no indico que es un cuadrado y me refiero a un cuadrilátero, la medida de los ángulos: 90°. •Hay una única posibilidad. 4 cm D 16) C 5 cm Se pueden construir diferentes paralelogramos con dos lados que miden 4 cm. Si se quiere dibujar un único cuadrilátero, hay que fijar la medida del otro par de lados y del ángulo comprendido entre dos lados. 3 cm c) Por ejemplo: A 4 cm B 5c m Para conversar juntos •Los instrumentos de geometría que se utilizaron son la regla graduada, y el transportador o la escuadra. La construcción es única: un trapecio rectángulo. 4 cm Se pueden construir diferentes paralelogramos. No se puede dibujar un único cuadrilátero, porque no se conoce la medida del ángulo comprendido entre un par de lados. d) Por ejemplo: 4 cm 17)1. Tracen un segmento AB que mida 5 cm. 2. Con vértice en A, y con uno de los lados que coincida con AB, tracen un ángulo de 45°. En el otro lado marquen el extremo C a una distancia de A de 7 cm. 3. Desde C, tracen un segmento en el mismo sentido y dirección que AB que mida 5 cm. Al otro extremo llámenlo D. 4. Unan B con D. 4 cm Desafío Hay 14 cuadrados. 18)Producción personal. Puedo construir diferentes cuadriláteros: trapecio rectángulo como el de la imagen, trapecio isósceles, rombo, romboide, paralelogramo propiamente dicho, rectángulo y cuadrado. Para que la figura sea única debo indicar, por ejemplo en el caso del cuadrado, que los ángulos miden 90°. e) Producción personal. f) Por ejemplo: 6 cm 3,5 cm 19)Para la primera figura: Dibujen una circunferencia de radio 1,7 cm. Tracen en la figura dos diámetros perpendiculares. Para la segunda figura: Dibujen una circunferencia de radio 1,7 cm. Tracen un diámetro de la circunferencia. Tracen un segmento paralelo al diámetro señalado, a una distancia de 7 mm, aproximadamente. Para conversar juntos •Las instrucciones pueden variar. •En la primera figura los diámetros forman un ángulo de 90°. •En la segunda figura el diámetro y el otro segmento son paralelos. 20) Para conversar juntos •No dibujaron todos el mismo paralelogramo porque no tenemos la medida del ángulo comprendido entre un par de lados, necesaria para que la construcción sea única. A C 4 cm B D a) AB // CD y AC // BD. b) AB ⊥ AC, AB ⊥ BD, CD ⊥ AC, CD ⊥ BD, AD ⊥ BC. g) 21) A 3 cm Se construye un único cuadrado porque se indica la medida de los lados. 36 Los conocedores B 22)Para trazar dos rectas perpendiculares utilizando una escuadra se puede proceder de la siguiente manera: 31)Por ejemplo, 30, 45, 75 y 105. 32)Por ejemplo, 28, 112 y 196. 33)342: 1, 2, 3, 6, 19, 38, 57, 114, 171, 342. 128: 1, 2, 4, 8, 16, 32, 64, 128. 250: 1, 2, 5, 10, 25, 50, 125, 250. 34)6: Por ejemplo, 12, 18, 24, 30, 36. 13: Por ejemplo, 13, 26, 39, 52, 65. 3: Por ejemplo, 9, 12, 15, 18, 21. 23)a) No es posible construir el triángulo, porque la suma de las medidas de los ángulos interiores de un triángulo debe dar 180° y, en este caso, hay dos ángulos que miden 100°. b) 35º 70º 35)12, 21, 22 y 31. 36)a) Cociente 780 y resto 0. b) Cociente 78 y resto 0. c) Cociente 7 y resto 800. d) Cociente 520 y resto 0. e) Cociente 52 y resto 0. f) Cociente 5 y resto 200. g) Cociente 198 y resto 7. h) Cociente 19 y resto 87. i) Cociente 1 y resto 987. 37)181. 5 cm c) No se puede construir un triángulo porque dos ángulos suman 180° y el tercero mediría 0°, lo cual es imposible. 38)No es posible, porque el resto debe ser menor que el divisor. Para conversar juntos •Un triángulo no puede tener dos ángulos interiores obtusos porque significaría que la suma de las medidas de los ángulos sería mayor que 180°. •Sí puede tener dos ángulos interiores agudos porque cada uno sería menor que 90° y, sumadas sus medidas, el valor obtenido sería inferior a 180°. 39)Si quiere darle la misma cantidad de potes a cada nieto, deberá regalarle a cada uno 4 potes. 24)La suma de los ángulos interiores de un rectángulo mide 360°. a) Quedan formados 2 triángulos. b) La suma de las medidas de los ángulos interiores de cada uno de los triángulos mide 180°. 25) 41) A B C D AB // CD, AC // BD. AB ⊥ AC, AB ⊥ BD, CD ⊥ AC, CD ⊥ BD, AD ⊥ BC. 85º 30º 40)Lo máximo que podrá comer cada uno serán 4 1/4 galletitas. 65º 42)Por ejemplo: m 26)Repartí 12 caramelos entre 6 chicos Repartí una pizza entre 4 chicos Repartí un kilo de helado entre 5 chicos Repartí 30 lápices entre 3 chicos Repartí 12 figuritas entre 2 chicos 1/2 1/3 1/4 1/5 1/6 27)Deben quedar pintados 6 autitos de color rojo, 4 de color verde y 2 de color azul. 28)1/2, 2/3, 2/5, 1/3, 1/4 y 1/2. 29)Por ejemplo: 6, 8 y 15. Para encontrar estos números, se puede pensar en la multiplicación de dos números primos, por ejemplo: 3 × 7; 21 solo tiene tres divisores, además del 1: 3, 7 y 21. 30)En este caso solo podemos considerar los números primos, por ejemplo: 7. El 7 tiene como divisores a 7 y 1. Siempre los divisores serán 1 y el mismo número. cm 5c 9 cm 47º 4 Para conversar juntos •No construyeron todos el mismo triángulo, porque pueden variar las medidas de los lados. Los triángulos obtenidos serán semejantes, pero no congruentes. a) En los primeros dos casos, no se dibuja una única figura, porque depende de las medidas y formas que se consideren. Solo en el tercer caso la figura es única. b) En el primer caso se puede dibujar un trapecio isósceles, un rectángulo, un rombo, un paralelogramo propiamente dicho o un cuadrado. En el segundo caso se puede dibujar un cuadrado o un rombo. Y en el tercero, un paralelogramo propiamente dicho. 43)1. Dibujen un rectángulo de 4,4 cm × 2,2 cm de lado. El lado de 4,4 cm debe ser paralelo al borde horizontal de la hoja. Paralelo al lado de 2,2 cm y por el punto medio del lado de 4,4 cm, tracen un segmento de 2,2 cm. Se observarán 2 cuadrados dibujados. 2. En el primer cuadrado, y de lado a lado, tracen un segmento paralelo al lado que queda paralelo al borde horizontal de la hoja y a 5 mm del lado superior del cuadrado. 3. En el segundo cuadrado, tracen la diagonal que va desde el vértice inferior izquierdo hasta el vértice superior derecho. 4. Tracen desde el vértice inferior derecho del segundo Los conocedores 37 cuadrado un segmento paralelo a la diagonal anteriormente trazada y con la misma medida. 5. Unan el extremo superior derecho del segundo cuadrado con el vértice del último segmento trazado que quedó libre. 7) 0 1/2 1 3/2 2 3 44)a) No. b) No. c) Sí. 8) 45)a) 2,8 35º cm 2/2 0 4,5 cm Se puede dibujar un único triángulo porque tengo tres datos: los lados y el ángulo comprendido. b) Siempre queda formado un triángulo equilátero de lado 4 cm. Capítulo 7 1) En los cuadrados 1, 3 y 4. 1/4 2/4 1 4/4 4/2 6/4 2 8/4 3 Para conversar juntos •Porque 1/2 y 2/4 son equivalentes. Si considero el mismo entero, 1/2 y 2/4 se encuentran a la misma distancia de 0. •Porque 2/2 y 4/4 son equivalentes. Además, puedo decir que tengo el mismo entero y en un caso tomo 2 de las 2 partes iguales en la que está dividido el entero, y en el otro 4 de las 4 partes iguales en la que está dividido el entero. Lo mismo sucede con 4/2 y 8/4. •Por ejemplo, cuando considero el mismo tamaño, es lo mismo “comerme 3/2 que 6/4 de pizza”. 2) 9) 3) 2/4 4/8 3/6 5/10 4) 10)2/6. 11) Sí, es verdad. Para conversar juntos •Observando que estuviera pintada una de cuatro partes equivalentes. •Para partir en tres partes iguales, por ejemplo, dividimos uno de los lados en tres partes de igual medida (marcamos dos puntos en el lado) y luego trazamos los segmentos paralelos, y de igual medida a los otros lados que tienen uno de los extremos en los puntos marcados. 5) 1/5 es una cantidad que entra 5 veces en un entero. 1/2 es mayor que 1/4 porque, considerando el mismo entero, cuando divido en 4 partes iguales, la parte es más chica que cuando divido en 2 partes iguales. 6) 12)a) 4/5. b) Le sobraron 6/10, que es más que la mitad. c) Tiene razón. Le falta pintar 3/8. Para conversar juntos •1/5 + 4/5 = 5/5 •6/10 + 4/10 = 10/10 •5/8 + 3/8 = 8/8 Desafío Es posible, porque dependerá del tamaño de ambos. Para que podamos decir que 1/3 es menor que 1/2, los enteros que considero tienen que ser equivalentes en medida. 13)3/4, 2/4 y 1/4, respectivamente. Para conversar juntos Hay más de un dibujo posible, por ejemplo, para la primera figura: 14)a) 2/3. b) 1/2. c) 3/5. d) 4/6 e) 4/8. f) 2/3. g) 1/2. h) 3/5. i) 4/6. j) 4/8. 15)a) 10/8 se pasa 2/8 de un entero. 10/8 – 8/8 = 2/8 o 10/8 – 2/8 = 8/8 = 1. b) 3/2 se pasa 1/2 de un entero. 3/2 – 2/2 = 1/2 o 3/2 – 1/2 = 2/2 = 1. c) 9/6 se pasa 3/6 de un entero. 9/6 – 6/6 = 3/6 o 9/6 – 3/6 = 6/6 = 1. d) 5/3 se pasa 2/3 de un entero. 5/3 – 3/3 = 2/3 o 5/3 – 2/3 = 3/3 = 1. 38 Los conocedores Para conversar juntos •Si el numerador es mayor que el denominador, la fracción es mayor que 1. Si el numerador es menor que el denominador, siempre la fracción es menor que la unidad. 16)a) 4/3 y 7/3, respectivamente. b) 6/4 y 10/4, respectivamente. 17)a) 10/8. b) 13/10. c) 10/5. d) 5/4. e) 6/2. f) 11/3. 18)a) V. b) V. c) F. d) F. e) V. f) F. Para conversar juntos •Para llegar a la fracción que falta para completar el entero (si es menor que la unidad) nos podemos fijar en cuánto le falta al numerador para tener el mismo valor que el denominador y luego le sumamos tantas veces el valor del denominador como sea necesario para poder llegar al entero buscado. •Si la fracción es mayor que la unidad, procedemos del mismo modo. Observamos cuánto le falta al numerador para llegar a un múltiplo del denominador, de manera que obtengamos el entero buscado. Producción personal Producción personal Producción personal Producción personal Producción personal Producción personal Calendario: mes de septiembre con el 1 y el 23 señalados Producción personal 25)El peso de un bebé: c. 3 m de madera: i. 200 g de salame: j. El peso de una cadenita de plata: j. 30 minutos: e. El largo de un escritorio: h. 36 grados de temperatura corporal: l. 2 horas: e. 2 grados de temperatura ambiente: d. 1 1/2 l de agua: a. El peso de una bolsa de cebollas: k. 1/4 l de yogur: a. La temperatura de un horno encendido: b. La cantidad de harina para hacer una torta: a. El largo de tu dedo meñique: g. La tela necesaria para un vestido: f. 26)Es correcto. 27)Por ejemplo, año, mes, semana, día, hora, minuto y segundo. 28)a) 12 meses. b) 7 días. c) 24 horas. d) 60 minutos. e) 60 segundos. f) 30 minutos. g) 15 minutos. 19)a) 7/8. b) 10/9. c) 7/5. d) 6/6. e) 3/2. f) 10/3. 20)a) 3/4. b) 1/2. c) 3/4. Para conversar juntos •En el caso de que no tenga iguales numeradores o denominadores, puedo buscar fracciones equivalentes a las dadas, de forma tal que ambas, por ejemplo, tengan el mismo denominador. 21)Con verde: 2/3, 3/4, 1/2, 2/5, 2/8. Con naranja: 5/3, 9/8, 5/2, 9/5, 10/6, 7/4. Con azul: 4/4, 2/2, 3/3, 8/8, 6/6. 29)En el reloj digital se marcan las 24 h. Por ello podemos identificar si se refiere a las 8 de la mañana o a las 8 de la noche. En el reloj de agujas solo tenemos indicadas 12 horas. Para conversar juntos •El día empieza a las 0 horas. •Decimos tres y media porque pasó media hora de las tres. Decimos siete menos cuarto porque falta 1/4 de hora para llegar a las siete. 30)Lo esperó 30 minutos. Tardaron 15 minutos en llegar. 22)a) Recorrió 1/6 más Mónica. b) Leyó más Lucía. c) Plantó menos Néstor. Para conversar juntos •La que da más trabajo es la situación del inciso c, porque necesito determinar las fracciones equivalentes apropiadas para poder comparar las fracciones. El largo de una manguera de regar. Diez cebollas. Los maníes de una bolsa. El agua de un balde. Cuánto aumentó de peso un tigre bebé La altura de una estatua. El contenido de un tanque de nafta. En metros × En kilos En litros × × 75 cm de cinta bebé 4 1/2 m de tela 33)a) V. b) F. c) V. d) F. e) F. f) V. g) F. h) V. 35)1/3, 7/4 y 5/2. 36)Andrés envasó 8 frascos de dulce y le quedaron 6 frascos. × × × × 37)Le sobraron 4/10 de tela, es decir 4 metros de tela. Esa cantidad es menor que la mitad. 38)Deben dibujarse 8 tacitas más. 39)Con verde: 1/3, 1/5, 2/6. Con naranja: 4/3, 10/8, 7/5, 10/9. Con azul: 5/5, 7/7. 24) 3 metros de elástico 32)a) 2/10. b) 5/10. c) 2/4. d) 2/8. e) 4/8. f) 2/6. 34)a) Por ejemplo, 1/5, 3/7, 10/11 y 5/9. b) Por ejemplo, 7/3, 12/7, 9/4, 8/5. c) Por ejemplo. 4/4, 12/12, 13/13, 20/20. 23) Longitud 31)Hay 15 minutos. Peso Capacidad Tiempo Reloj de pared 250 cm de 1/2 kilo de yerba que marca las 3 crema horas Reloj de 1 kilo de pulsera que 1 litro de leche harina marca las 15 horas Reloj digital 200 g de 1.250 ml de que marca las manteca agua 3:00 p. m. 3 40)Por ejemplo: a) La carne, el pan, el fiambre. b) La leche, el agua, el detergente. c) La cinta de bebé, la cantidad de papel para empapelar una pared, la cinta de embalar. d) La carga de un camión, un rinoceronte, la cantidad de trigo de una cosecha. e) La distancia entre dos ciudades, el perímetro de un campo cultivado, el largo de un camino. f) La manteca, el arroz, los fideos. g) La esencia de vainilla, el agua, la gaseosa. h) un lápiz, el largo de una hoja de carpeta, el perímetro de un azulejo. Los conocedores 39 Capítulo 8 15)1 3/4, 7/4, 14/8, 21/12, 3/2 y 1/4. 1) 16)Los dos tienen razón porque 3/5 y 6/10 son equivalentes. 0 1/3 4/6 111/9 2 14/6 3 17)El segmento mide 6 cm. Entonces, si debo dibujar un segmento que mida 2/3 del dado, deberá medir 4 cm. En el caso de 7/6: 7 cm, y para 4/6: 4 cm. 2) 18)3/4 es más grande que 3/5. 1/4 es más chico que 3/8. 0 1/5 1 19)a) En total regaló 3/6 (o 1/2) de tarta. b) Se comieron en total 6/4 de tarta, es decir 1 tarta y 1/2. c) Se comieron en total 4/6 (o 2/3) de torta. d) Le quedaron 3/4 del chocolate. e) Le queda aún 2/4 (o 1/2) de chocolate. f) Le queda aún 3/6 (o 1/2) de chocolate. 2 3) 0 1/4 2 Para conversar juntos Por ejemplo, 4) A: 2/3. B: 4/3. Para conversar juntos •Si en una recta están ubicados 1 y 1/2 podemos ubicar el 0, porque la distancia entre 0 y 1/2 es la misma que entre 1/2 y 1. •Si están ubicados 1/2 y 2 también es posible porque entre 1/2 y 2 hay tres medios. Entonces, la tercera parte de la distancia entre 1/2 y 2 es la distancia entre 1/2 y 0. 5) 25/100 0 1 2 + 2/3 4/6 = 9/6 Para conversar juntos a) 10/5 5/10 5/6 25/10 3 6) 2/6 0 1/10 + 1/6 = 3/6 = 1/2 b) 1 7) 0 5/10 1 3/4 Para conversar juntos •1/2 se ubicaría en el mismo lugar que 5/10 porque 1/2 y 5/10 son fracciones equivalentes. 8) 4/8 0 1/2 + 3/4 d) 5/4 6/4 = 1 2/4 = 1 1/2 1/4 1 – 1/4 = 4/4 – 1/4 = 3/4 1 1/4 1 = 2 e) 1/4 1/4 9) 2/4 y 4/8. 1/4 1/4 3/4 1/4 3/4 – 1/4 1/4 1/4 = 1/4 2/4 1/2 = 1/2 10)Los dos dicen lo mismo porque 1/5 es equivalente a 2/10. 11)Por ejemplo: 2 1/2 - 1 1/2 - 1/2 1 1/2 - 1 1/2 - 1 1/2 1 - 1 - 1 - 1 1/2 1/2 - 1/2 - 1/2 - 1 1/2 - 1 1/2 2 1/2 - 1 - 1 1 - 1 - 1 1/2 - 1/2 - 1/2 12)Hay 3/4 litros de agua. 13)Compró 6/4 kilogramos de pan. 14)2/10, 1/5, 40/200 y 60/300. 40 Los conocedores 20)a) 1/2. b) 11/10. c) 1/8. d) 3/8. e) 2/9. f) 3/4. g) 7/10. h) 2/3. i) 1/3. j) 1/8. k) 13/10. l) 3/2. m) 2. n) 25/11. ñ) 2/5. Desafío 0 1/2 2/3 1 2 21)a) m. b) km. c) mm. d) cm. e) m. f) m. g) mm o cm. h) mm o cm. i) m. j) km. 22)En todos los casos las medidas realizadas con la regla son aproximadas y dependen del objeto elegido. El grosor de la guía de teléfonos: valor estimado: 5 cm; valor con regla: 4 cm y 1 mm. El ancho de tu silla: valor estimado: 50 cm; valor con regla: 46 cm. El largo de tu escritorio: valor estimado: 1 1/2 metros; valor con regla: 1 metro y 20 cm. La altura de la puerta del aula. Valor estimado: 2 metros; valor con regla: 1 metro y 90 cm. 23)Considerando las medidas realizadas con la regla: 4 cm y 1 mm; 46 cm; 1 m y 20 cm; 1 m y 90 cm. Para conversar juntos •En general las estimaciones coincidirán con las mediciones realizadas. •1/2 m = 50 cm. 1/4 m = 25 cm. 1 1/2 m = 150 cm. Para conversar juntos •1 m equivale a 1.000 mm. 1 km equivale a 100.000 cm. 24)a) Por ejemplo, más que 1 metro: el alto de una puerta, el largo de un pizarrón, el largo de un auto. Menos que 1 metro: el ancho de un cuaderno, el ancho de una impresora, el largo de un libro. Cerca de un metro: el largo del escritorio, el ancho de la ventana, el ancho de la puerta. b) Por ejemplo, más que un centímetro: una goma de borrar, un lápiz, el alto del pote de yogur. Menos que 1 centímetro: el largo del tornillo de los anteojos, el diámetro de la pupila del ojo, el ancho de la uña del dedo meñique. Cerca de 1 centímetro: el ancho del dedo anular, un gancho para abrochar un par de hojas, el ancho de una de las teclas de la computadora. Para conversar juntos •Los niños podrían decir que para realizar las estimaciones tuvieron en cuenta el tamaño de los objetos. 33)a) 500 ml. b) 250 ml. c) 750 ml. 34)a) Menos que 1 litro. b) Más que 1 litro. c) 1 litro. d) Menos que 1 litro. 35)Por ejemplo: Más que 1 litro: la cantidad de agua de una pileta, la cantidad de agua de una laguna, la cantidad de líquido de un barril. Cerca de 1 litro: la cantidad de agua que contiene una pava, la cantidad de leche que entra en una licuadora, la cantidad de jugo que contiene una jarra. Menos que 1 litro: la cantidad de té de una taza, la cantidad de líquido que contiene un frasco de jarabe, la cantidad de líquido que entra en un plato para sopa. 36) 0 3/9 3/6 2/3 1 37) 0 1/2 3/4 1 38)a) 3/4 = 6/8 = 9/12 = 15/20. b) 5/6 = 10/12 = 15/18 = 20/24. c) 1/5 = 2/10 = 3/15 = 4/20. d) 2/3 = 4/6 = 6/9 = 8/12. e) 4/3 = 8/6 = 12/9 = 20/15. 25)a) g. b) kg. c) t. d) g. e) t. f) kg. 39) 26)a) 1 t. b) 5 g. c) 4 kg. d) 100 g. 27)Un lápiz, la lana para hacer una bufanda, veinte naranjas, una jirafa. 40)El segmento rojo mide aproximadamente 1/2 del segmento verde y 2 veces el segmento azul. Para conversar juntos •Los chicos podrían decir que para realizar las estimaciones tuvieron en cuenta: la experiencia personal, el tamaño y el peso de los objetos (porque conocen su medida aproximada), etc. 41)a) V. b) F. c) F. d) F. 28)a) 500 g. b) 250 g. c) 1.500 g. d) 500 kg. e) 250 kg. f) 1.500 kg. 44)La tira roja mide 3 veces la tira verde y 6/7 de la tira azul. 29)Por ejemplo, más que 1 kilogramo: un televisor, una silla, un escritorio. Cerca de 1 kilogramo: un libro, una olla, una pava con agua. Menos que 1 kilogramo: una taza, un libro, un plato. 42)a) 2. b) 1 1/2. c) 1/2. 43)El segmento unidad mide 6 cm. 45)a) 7/10 > 3/5. b) 1/2 = 5/10. c) 2/3 < 3/4. d) 1/3 < 2/4. e) 5/6 > 3/4. f) 1/2 > 3/10. 46)Laura comió más. 47)Completaron 13/20 del álbum y les falta completar 7/20. Para conversar juntos •Los niños podrían decir que tuvieron en cuenta el peso de objetos que conocen. Por ejemplo: “conocemos algo que pesa 1 kg y luego lo comparamos con otros objetos que pesan más o menos que 1 kg”. 30)a) l. b) ml. c) ml. d) l (kl). e) l (hl). 48)Entre las dos comieron 5/6 del alfajor. 49)Llevó $ 24 al cine. 50)a) 1/2. b) 2/3. c) 3/4. d) 1/2. e) 3/4. f) 1/4. g) 2/3. h) 34/7. i) 9/5. j) 5/4. k) 3/4. l) 1/10. m) 11/6. n) 13/5. ñ) 1/3. o) 4/5. p) 1/2. q) 3/5. r) 7/4. s) 19/5. 31)a) 1 l. b) 1.000 l. c) 1/4 l. 51)Entre los dos compraron 1.250 g de carne. 32)Una taza, una botella de agua mineral, el tanque de agua de una casa. 52)Manuela consume más leche. Los conocedores 41 53)Lucía comió 5/12 del chocolate. Capítulo 9 1) a) 6 pesos con 50 centavos. b) 1 peso con 25 centavos. 2) $ 1,10. 3) Decir “un peso veinte” es lo mismo que decir “un peso con veinte centavos”. Se escribe: $ 1,20. 4) a) $ 1,50. b) $ 1,25. 5) a) $ 1,20. b) $ 0,65 (o 65 centavos). c) $ 3,70 el precio de 10 botones. $ 0,37 el de 1 botón. d) Si llevan 10 botones sueltos, pagan $ 1,50. Si llevan 100, $ 15. 6) a) 0,3. b) 2,3. c) 0,03. d) 0,23. e) 0,003. f) 0,023. 13)a) Le alcanzará el dinero porque el costo total sería $ 69,40 y llevó $ 75,70. b) El libro le costó $ 27,55. c) $ 80. d) Le dieron de vuelto $ 14,62. Desafío 6,35 y 6,26. e) 50,75. Para conversar juntos •91,35 si compra 5 y 101,5 si compra 6. f) Le darán 53,5 de vuelto. Para conversar juntos •Como la oferta no aclara que las tres revistas deben ser iguales, los chicos podrían responder y justificar de dos maneras diferentes: 1. Paga $ 71,80, porque las cuatro revistas son diferentes; 2. Paga otro valor, ya que considera la mitad del valor de alguna de las 4 revistas, seguramente la más cara. 7) a) 1,6. b) 0,6. 14)a) 0,9. b) 0,5. c) 0,40. d) 0,35. e) 0,25. f) 0,75. 8) a) Liliana puede usar, por ejemplo, 5 monedas de 50 centavos y 3 de 10 centavos; o 10 monedas de 25 centavos y 3 de 10 centavos. b) Ana puede usar, por ejemplo, 7 monedas de 50 centavos y 1 de 25 centavos; o usar 6 monedas de 50 centavos y 3 de 25 centavos. 15)a) 0,8. b) 1. c) 0,20. d) 0,10. e) 1,25. f) 0,25. Para conversar juntos •Ambos tienen razón. Es lo mismo sumar 0,2 que 0,20 a 0,60 para obtener 0,8, porque 2/10 es equivalente a 20/100. 9) a) 10. b) 20. c) 40. d) 100. e) 200. 16)a) 6,75. b) Entre 10 y 11. c) 6,15. 10)a) 20 monedas. b) 10 monedas. c) 6 monedas. d) 23 monedas. e) 14 monedas. f) 8 monedas y me darían 5 centavos de vuelto. Para conversar juntos •Sí, porque una moneda de $ 1 es equivalente a dos de 50 centavos. •En el caso de las monedas de 10 centavos, la cantidad de monedas de 10 centavos será 10 veces mayor que las de $ 1, porque 10 monedas de 10 centavos equivalen a una de $ 1. •En el caso de las monedas de 5 centavos, la cantidad de monedas de 5 centavos será 20 veces mayor que las de $ 1, porque 20 monedas de 5 centavos equivalen a una de $ 1. •En el caso de las monedas de 25 centavos, la cantidad de monedas de 25 centavos será 4 veces más que las de $ 1 porque 4 monedas de 25 centavos equivalen a una de $ 1. 11)a) $ 2,05. b) $ 3,1 o $ 3,10. Para conversar juntos •En el segundo caso hay dos carteles posibles porque 3,1 = 31/10 y 3,10 = 310/100 = 31/10. 42 17)18,67. 18)La segunda y la cuarta cuenta están bien resueltas. La primera cuenta está mal resuelta porque hace 6 + 8 = 14, en lugar de 60/100 + 80/100 = 140/100 = 1,4. La tercera cuenta está mal resuelta porque hace 13 + 7 = 20, en lugar de 13/100 + 70/100 = 83/100 = 0,83. Para conversar juntos •16,50. 19)250 cm y 240 cm. Para conversar juntos •Para averiguar la medida de cada contorno podemos sumar las medidas de todos los lados de la figura. Otra manera posible es hacer: 70 cm × 2 + 55 cm × 2, en el primer caso, y 60 cm × 4 en el segundo. 20)15 cm. 12)a) El producto que tiene un mayor precio son las agujas de tejer. El más barato son los alfileres de gancho. b) 0,09; 0,1; 0,50; 1,25; 1,9; 4,15; 4,20. Para conversar juntos •Para el paralelogramo necesitamos la medida de los lados diferentes. Para el trapecio, las medidas de la base mayor, de la base menor y la de los lados iguales. Para conversar juntos •$ 1,9 es mayor que $ 1,25 porque 90 centavos son más que 25 centavos. 21)Para cada servilleta deberá comprar 74 cm de puntilla (73,40 cm). Si quisiera colocarle puntilla a 6 servilletas, 444 cm (440,40 cm). Desafío Por ejemplo, 1,51; 1,56 y 1,58. Por ejemplo, 2,83. 9,91. 22)No le alcanzará la cinta porque necesita 7,60 m y solo compró 6 m. Los conocedores Para conversar juntos •Si el perímetro de un rectángulo es de 32 cm, sus lados pueden medir 10 cm y 6 cm, respectivamente. La respuesta no es única, por ejemplo otra medida podría ser: 4 cm y 12 cm, respectivamente. 23)Para cubrir la pared necesitará 534 azulejos rojos, aproximadamente; o 300 azulejos verdes. Para conversar juntos •Cubre exactamente la pared con los verdes. Desafío 39)a) 57,09. b) 79,44. c) 45,67. d) 99,05. 40)Cada lado mide 3,5 cm. 41)a) 12 cm. b) 16 cm. 42)Se puede dibujar otro rectángulo de lados que midan 8 cm y 4 cm, respectivamente. 43)Por ejemplo, el cuadrado de lado 4 cm. Hay varias respuestas posibles, es necesario buscar todas las multiplicaciones de dos factores que den por resultado 16. Ficha 1 1) a) 9.420. b) 2.049. 24)Necesitaría 267 azulejos grises, aproximadamente, y 240 azulejos marrones. 2) a) 87.530. b) 30.578. 3) 2.049, 9.420, 30.578, 87.530. Para conversar juntos •Cubre exactamente la pared con los azulejos marrones. 25)Necesitaría, aproximadamente, 235 azulejos grises. 4) • Dos mil cuarenta y nueve. • Nueve mil cuatrocientos veinte. • Treinta mil quinientos setenta y ocho. • Ochenta y siete mil quinientos treinta. Para conversar juntos •Todos obtuvieron una cantidad aproximada, porque 450 no es divisor de la cantidad que representa la superficie que queda por cubrir. 5) 452, 425, 542, 524, 245, 254. 26)2 azulejos rojos equivalen a 1 gris. 1) a) 1.288. b) 1.704. c) 1.529. d) 1.802. e) 1.455. 27)Es correcto lo que dice, porque si duplico la superficie necesito el doble de baldosas para cubrir el patio. 2) a) 850 b) 493 c) 607 d) 375 e) 1.900 28)En la primera columna: 4,1 - 4,2 - 4,3 - 4,4 - 4,5 - 4,6 - 4,7 4,8 - 4,9 - 5. En la segunda columna: 4,1 - 4,11 - 4,12 - 4,13 - 4,14 - 4,15 - 4,16 - 4,17 - 4,18 - 4,19. 29)En la primera columna: 4,1 - 4 - 3,9 - 3,8 - 3,7 - 3,6 - 3,5 3,4 - 3,3 - 3,2. En la segunda columna: 12,1 - 12,09 - 12,08 - 12,07 - 12,06 - 12,05 - 12,04 - 12,03 - 12,02 - 12,01. 30)Gastó en total $ 45,05 y le dieron de vuelto $ 4,95. 31)$ 5. 32)Puede gastar $ 13,75. 33)Una docena costará $ 15. 34)Le dieron de vuelto $ 26,50. Le hubieran dado de vuelto $ 17. 35)a) 6,5. b) 27,07. c) 2,5. d) 0,5. e) 3,5. f) 1,20. g) 28,90. h) 1,75. 36)a) 1,5. b) 1,75. c) 2,5. d) 2,75. e) 1,6. f) 2,6. g) 3,6. h) 4,6. 37)a) 84,2. b) 60,2. c) 37,14. d) 19. e) 4,5. f) 7,75. 38)a) 33. b) 36. c) 29. d) 1. Ficha 2 1.850 – 1.000 1.493 – 1.000 1.607 – 1.000 1.375 – 1.000 2.900 – 1.000 Ficha 3 1) 980 – 680 = 300, 980 – 300 = 680 y 6.800 + 3.000 = 9.800. 2) a) 1.800 + 200 + 100 = 2.000 + 100 = 2.100. b) 2.700 + 300 + 600 = 3.000 + 600 = 3.600. c) 1.400 + 600 + 200 = 2.000 + 200 = 2.200. d) 2.500 + 500 + 200 = 3.000 + 200 = 3.200. e) 4.900 + 100 + 500 = 5.000 + 500 = 5.500. f) 3.800 + 200 + 300 = 4.000 + 300 = 4.300. g) 3.900 + 100 + 300 = 4.000 + 300 = 4.300. Ficha 4 1) Cálculo 5.550 + 10 7.208 – 869 740 – 10 93.764 + 17.906 890 – 100 10.000 – 8.479 20.000 + 5.000 25.000 + 376 48.000 + 1.000 48.000 + 1.235 Con calculadora Mentalmente 5.560 6.339 730 111.670 790 1.521 25.000 25.376 49.000 49.235 Los conocedores 43 2) a) Por ejemplo, 1.450 + 300 = 1.750 y 162 + 20 = 182. b) Por ejemplo, 4.563 + 1.789 = 6.352 y 389 + 177 = 566. 2) Por ejemplo, Lucía tiene 30 libros más que Sofía. Si Sofía tiene 102 libros, ¿cuántos libros tiene Lucía? Ficha 5 Ficha 9 1) a) Rectángulo. 4 lados y 4 vértices. 1) A las centenas 2.100 5.300 2.900 9.200 5.300 1.900 1.900 A las decenas b) Rombo. 4 lados y 4 vértices. 2.133 5.289 2.914 9.162 5.321 1.891 1.899 2.130 5.290 2.910 9.160 5.320 1.890 1.900 A las unidades de mil 2.000 5.000 3.000 9.000 5.000 2.000 2.000 2) Aproximadamente necesito $ 20 + $ 20 = $ 40. Pero, para que alcance el dinero al comprar, el redondeo debe hacerse siempre a la decena superior. c) Triángulo. 3 lados y 3 vértices. No es posible trazar las diagonales. d Trapecio isósceles. 4 lados y 4 vértices. Ficha 10 1) a) Obtuso. b) Agudo. c) Agudo. d) Recto. e) Obtuso. 2) Por ejemplo: e) Cuadrado. 4 lados y 4 vértices. obtuso agudo recto Ficha 11 Ficha 6 1) Tiene dos pares de lados paralelos. Todos sus ángulos son rectos. Los lados miden 2 cm y 4 cm, respectivamente. 2) a) Tienen 6 lados iguales. b) Tiene 4 lados y no son todos iguales. Ficha 7 1) a) No, tengo tantas unidades como el número indicado. Por ejemplo, el número 365 tiene 365 unidades. b) 8. c) 978. d) No, tengo tantas decenas como el resultado entero obtenido al dividir el número por 10. Por ejemplo, el número 3.847 tiene 384 decenas (3.847 : 10 = 384,7). e) 7. f) 97. g) No, tengo tantas centenas como el resultado entero obtenido al dividir el número por 100. Por ejemplo, el número 4.535 tiene 45 centenas (4.535 : 100 = 45,35). h) 9. i) 9. Ficha 8 1) a) Estimación: 90° y medida: 90°. b) Estimación 130° y medida: 120°. c) Estimación: 60° y medida: 60°. 2) 35º 95º Ficha 12 1) a) Agudo. 45°. b) Recto. 90°. c) Obtuso. 110°. d) Agudo. 30°. e) Obtuso. 145°. 2) a) 80°. b) 130°. Ficha 13 1) a) DLXXIII. b) DCCCLII. c) MCXI. 2) a) 116. b) 444. c) 1.505. 1) a) Hay 230 libros de cuentos más que enciclopedias. b) Hay 135 diccionarios. c) Hay 300 novelas. 44 Los conocedores 105º 3) a) LXXXI. b) CIX. c) XLIX. Ficha 14 Ficha 18 1) Por ejemplo: 5 × 4 + 5 × 12 + 3 × 2 o 10 × 4 + 5 × 5 + 5 × 3 + 3 × 2. 2) Son posibles 30 combinaciones (5 × 6). 1) Producción personal. Ficha 15 1) a) Ficha 19 1) Luciano colecciona estampillas. Está armando un álbum. Si en cada página quiere pegar 35 estampillas y el álbum tiene 15 páginas, ¿cuántas figuritas podrá pegar en el álbum? 2) Laura organizó el precio de los alfajores en esta tabla: Alfajores 1 2 3 4 5 6 7 8 9 Precio $ 2,50 $5 $ 7,50 $ 10 $ 12,50 $ 15 $ 17,50 $ 20 $ 22,50 0 10 20 b) 0 50 100 150 200 c) 0 1.000 2.000 3.000 Ficha 20 1) a) R. b) P. c) R. Si Marcela quiere comprar 15 alfajores, ¿cuánto deberá pagar? Si Enzo pagó $ 12,50, ¿cuántos alfajores compró? ¿Y si pagó $ 25? 2) Marijó tiene 50 libros y quiere repartirlos en partes iguales entre sus 3 sobrinos. ¿Cuántos libros le dará a cada uno? ¿Quedarán algunos libros sin repartir? 3) Producción personal. 3) Germán tiene 500 libros. Si quiere guardar 75 en cada caja, ¿cuántas cajas necesita? ¿Le quedarán libros sin guardar? ¿Por qué? 4) Producción personal. Ficha 16 Ficha 21 1) a) 760. b) 7.600. c) 76.000. d) 1.380. e) 13.800. f) 138.000. g) 12.450. h) 124.500. i) 235.600. 2) 8×2×2×2 90 × 100 2.954 × 2 × 2 540 × 10 5.079 × 3 × 3 25 × 10 × 10 Mentalmente 64 9.000 Con calculadora 11.816 5.400 45.711 2.500 Ficha 17 Ficha 22 1) a) 89. b) 89. c) 89. d) 7.421. e) 3.852. f) 6.999. g) 22. h) 45. i) 83. j) 345. k) 823. l) 576. m) 12. n) 120. ñ) 1.200. o) 73. p) 989. q) 576. 2) Puedo armar 14 bolsitas. circunferencia Ficha 23 radio 1) di ám et ro 1) 1) a) 45 × 8 = 360, 360 : 8 = 45, 360 : 45 = 8. b) 67 × 9 = 603, 603 : 9 = 67, 603 : 67 = 9. c) 82 × 7 = 574, 574 : 7 = 82, 574 : 82 = 7. d) 96 × 5 = 480, 480 : 5 = 96, 480 : 96 = 5. e) 73 × 6 = 438, 438 : 6 = 73, 438 : 73 = 6. lado centro vértice ángulo 2) El diámetro mide 4 cm. 2) a) isósceles. b) equilátero. c) isósceles. d) escaleno. e) escaleno. f) isósceles. Los conocedores 45 Ficha 24 cm c) 3 1) a) Verde. b) Rojo. c) Rojo. d) Azul. e) Verde. f) Azul. 50º 2) 4 cm 3 cm d) acutángulo rectángulo obtusángulo 90º 4 cm 2) Producción personal. Ficha 25 1) a) 954.206. b) 437.309. c) 56.036. d) 749.108. e) 53.503. Ficha 30 1) Producción personal. Ficha 26 2) a) 5 cm cm Ficha 27 2 1) a) 2.793. b) 6.531. c) 1.356. d) 8.499. e) 5.750. f) 3.155. g) 2.006. h) 3.040. 6 cm 1) 1 $8 2 5 10 12 15 20 30 $ 16 $ 40 $ 80 $ 96 $ 120 $ 160 $ 240 4 Cantidad de entradas Precio por entrada cm b) 45º 2) Cantidad de paquetes Cantidad de galletitas 1 10 2 20 5 50 10 100 12 120 15 150 20 200 30 300 Ficha 28 1) Considerando que el resto puede valer 8, 7, 6, 5, 4, 3, 2, 1 o 0; los dividendos posibles son: 80, 79, 78, 77, 76, 75, 74, 73 o 72, respectivamente. 2) a) Está entre 100 y 1.000. Una forma de darse cuenta es dividir 3.960 por 10 (396) y luego por 3. El resultado será un número mayor que 100. b) Está más cerca de 200. Si dividimos 2.500 por 10, obtenemos 250; entonces al dividir por un número una unidad más grande, el resultado se encontrará entre 200 y 250. c) Está más cerca de 170. Si divido a 8.525 por 100 me da aproximadamente 85, y 85 × 2 = 170. Ficha 29 3 cm 1) a) No se puede construir. b) 6 cm 7 cm Ficha 31 1) a) Debe entregar a cada equipo 25 postales. No se puede seguir repartiendo. b) Puede gastar en cada regalo $ 25 y 50 centavos. c) Para cada mantel puede usar 1 metro y 25 centímetros. Ficha 32 1) a) 30: 1, 2, 3, 5, 6, 10, 15 y 30. b) 12: 1, 2, 3, 4, 6 y 12. 2) a) 7: por ejemplo, 14, 21 y 49. b) 5: por ejemplo, 15, 20 y 50. c) 4: por ejemplo, 16, 24 y 32. d) 11: por ejemplo, 22, 33 y 44. 3) a) Puede armar 1 móvil con 36 pajaritos. 2 con 18. 3 con 12. 4 con 9. 6 con 6. 9 con 4. 12 con 3. 18 con 2. 36 con 1. b) En cada móvil podría colocar 12 pajaritos. c) Si usara 9 pajaritos podría armar 4 móviles. Si usara 4 pajaritos por cada móvil podría armar 9 móviles. Ficha 33 1) 167 es el dividendo, 8 el divisor, 20 el cociente y 7 el resto. m 7c 2) a) Resto = 3. b) Cociente = 40. c) Divisor = 5. d) Dividendo = 182. 3) 200 × 15 = 3.000, 40 × 15 = 600, y 6 × 15 = 90. 46 Los conocedores Ficha 34 Ficha 38 1) Vértices: F, G, P, L Lados: FP, PL, GL, FG Ángulos: ^ F, ^ P, ^ G,^ L Diagonales: FL y GP 1) En el primer punto, corresponde 1/3; en el segundo, donde está ubicado el 1, 5/5, y en el tercero, 6/4. 2) 2) 0 6 cm Se pueden construir diferentes paralelogramos, porque se debería indicar la medida del otro lado consecutivo y la medida del ángulo entre los dos lados, por ejemplo. 3c m 6 cm También se pueden construir diferentes paralelogramos, porque aunque se indica la medida de los dos lados consecutivos, no se indica la medida del ángulo que forman entre ambos, por ejemplo. 1 5/4 3/3 4/4 2 5/2 3 3) 0 3) 2/4 1/4 1 2 4) No, porque 4/3 se encuentra a 1/3 de 1 y la fracción indicada representa 3/2. Ficha 39 1) 2/8. La cantidad no puede expresarse en medios porque es menor que 1/2. Ficha 35 2) 3/6, 2/4, 4/8, 5/10, 6/12. 1) a) Tiene un par de lados paralelos y desiguales, y los lados que no son paralelos son iguales. b) Tiene un par de lados paralelos y desiguales, y dos ángulos rectos. c) Tiene un par de lados paralelos y desiguales, y los lados que no son paralelos también son desiguales. 3) 2/6, 3/9, 4/12. Ficha 36 1) a) Quedaron 4 empanadas. b) Quedaron 8 metros. c) 5/8 es más que la mitad, es 1/8 más. Le falta pegar 3/8 de la guarda. 1) Para construir un único paralelogramo se necesitan los siguientes datos: dos lados consecutivos y una diagonal; dos lados consecutivos y el ángulo comprendido entre ambos; un lado, una diagonal y un ángulo; un lado y las dos diagonales. 2) La construcción es única, porque se indica la medida de los lados y, al decir que es un cuadrado, se sabe que sus ángulos son rectos. 3) En este caso, el rombo no va a ser único porque pueden variar las medidas de los ángulos. Por ejemplo, son posibles estos dibujos: 4) Por ejemplo, 1/2, 1/4, 3/6, 2/3. Ficha 40 2) a) 3/4. b) 1/6. 3) a) 3/2. 5/2 – 3/2 = 1. b) 1/5. 6/5 – 1/5 = 1. Ficha 41 1) a) Es verdad, porque 2/6 y 1/3 son fracciones equivalentes. b) No es verdad, porque 3/9 y 1/3 son fracciones equivalentes. c) Omar usó más cartulina, porque 3/4 es equivalente a 6/8 que es mayor que 3/8. 2) a) 2/8. b) 1/4. c) 1/4. d) 2/5. e) 2/10. f) 2/3. Ficha 42 Ficha 37 1) 1/3, 2/5 y 1/3, respectivamente. 1) a) Metros. b) Litro. c) Minutos. d) Kilo. 2) Ambos tienen razón, porque 2 m = 200 cm. 3) a) 933 km aproximadamente. b) 6.962 m. c) 1 tonelada aproximadamente. d) 34 litros aproximadamente. e) 600 minutos. 2) Van pintadas dos flores y una cuarta parte de la torta. 3) 1/2. Porque es equivalente a 2/4, que es mayor que 1/4. Los conocedores 47 Ficha 43 Ficha 48 1) a) 1) a) Se intenta que la cantidad sea exacta, pero muchas veces resulta aproximada porque en función de la consistencia esperada de la mezcla se agrega un poco más de leche. b) Aproximada, porque, por ejemplo, al poner alcohol en un trozo de algodón, no se considera una cantidad específica. c) Aproximada, porque no sabemos la cantidad exacta de jugo que consumirá cada persona. d) Exacta, porque conocemos la capacidad del envase. 0 1/2 5/10 1 1 1/2 15/10 2 25/10 2 1/2 3 b) 0 25/100 1/4 1/2 50/100 3/4 75/100 1 2) 2) a) Por bidón necesita 20 botellas. b) Compró 10 1/2 litros de gaseosa. Ficha 49 0 1/3 1/2 5/6 1 2 1) a) Diecisiete enteros y cinco décimos. b) Trece enteros y veinticinco centésimos. c) Catorce centésimos. d) Ocho centésimos. e) Doce enteros y tres centésimos. Ficha 44 2) a) 1,32. b) 0,32. c) 9,5. d) 9,05. 1) a) 25/100. b) 5/10. c) 75/100. d) 2/10. 3) a) 0,8 - 0,08 - 0,008. b) 3,5 - 0,35 - 0,035. 2) 4/10, 40/100, 2/5. 3) a) Compró 5 bolsas. b) Compró 15/4 kg de cebollas, es decir, 3 3/4 kg. Ficha 50 1) a) 300 centavos. b) 1.400 centavos. c) 11.100 centavos. d) 250 centavos. Ficha 45 2) a) $ 30,55. b) $ 62,50. c) $ 8,05. d) $ 11,10. e) $ 0,32. 1) a) 6/8 10/8 = 5/4 3) $ 62,50 - $ 30,55 - $ 11,10 - $ 8,05 - $ 0,32. 4/8 Ficha 51 b) 1/5 7/10 – 1/5 = 7/10 – 2/10 = 5/10 = 1/2 2) a) 3/5 + 8/10 = 3/5 + 4/5 = 7/5. Comieron en total 7/5 de pizza, es decir 1 pizza y 2/5 de pizza. b) Le quedó 1/4 de la resma. 1) a) Sí, le alcanza con $ 20. Para resolver el problema se puede redondear $ 2,05 a $ 2, y luego hacer $ 2 × 8 = $ 16. b) No le alcanza el dinero. $ 38,99 es casi $ 39, y $ 61,80 es casi $ 62. $ 39 + $ 62 = $ 101. 2) a) 91. b) 110. c) 50. d) 39. Ficha 46 Ficha 52 1) Los dibujos miden, de arriba hacia abajo: 10 cm, 7 cm y 5 cm. 1) a) Es correcta. b) El resultado correcto es 138,72. c) El resultado correcto es 175,04. d) El resultado correcto es 55,02. e) El resultado correcto es 65,97. f) Es correcta. 2) a) Aproximada. b) Exacta. c) Exacta. 3) En una cuadra hay, aproximadamente, 10.000 cm (100 × 100) o 100.000 mm (10.000 × 10). Ficha 47 Ficha 53 1) a) 70 cm y 62 cm. b) 70 cm × 3 + 62 cm × 3 = 132 cm × 3 = 396 cm = 3,96 m. 2) a) 28 cm (7 × 4). b) 16 cm (5 × 2 + 3 × 2). 1) a) Exacta (a veces puede ser aproximada). b) Aproximada. c) Puede ser exacta o aproximada. d) Aproximada. e) Exacta. 2) a) Entre las dos compraron 3 kg y 250 g de carne (o 3,250 kg). b) Compró 2 1/2 kg de fruta. Ficha 54 1) a) 40. b) 10. c) 5. 2) a) 34. b) 27. 48 Los conocedores