PROBLEMAS RESUELTOS
Anuncio
Tema 3
PROBLEMAS RESUELTOS
PROBLEMA 1
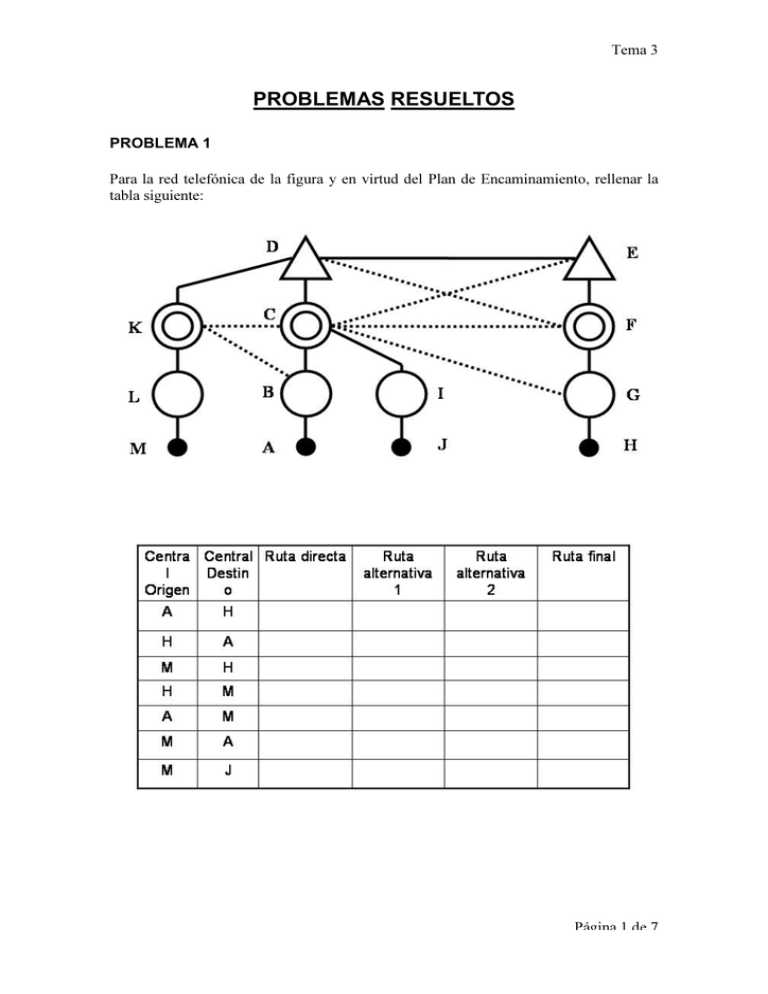
Para la red telefónica de la figura y en virtud del Plan de Encaminamiento, rellenar la
tabla siguiente:
Página 1 de 7
Tema 3
PROBLEMA 2
Para la red telefónica de la figura y en virtud del Plan de Encaminamiento, rellenar la
tabla siguiente:
Página 2 de 7
Tema 3
PROBLEMA 3
La figura representa parte de la estructura de una región telefónica junto al tráfico
intercambiado en la HC por las distintas centrales.
Las rutas finales se han dimensionado en base a una probabilidad de pérdida del 1% y
las secciones directas con una probabilidad de desbordamiento del 10%.
a) Rutas posibles con origen en A y destino en la central K. Ordénelas por
prioridad según las normas de encaminamiento en redes jerárquicas telefónicas.
b) Tráfico en la central A y con destino al sector telefónico definido por la central
primaria H
c) Tráfico en la central A y con destino a la provincia telefónica definida por la
central secundaria E.
d) Tráfico ofrecido a la sección directa B → H
e) Tráfico ofrecido a la sección directa B → E
f) Tráfico de desbordamiento en B.
g) Para el trámo B-C:
1º. Tráfico ofrecido
2º. Tráfico cursado
3º. Número de circuitos necesarios
4º. Número de pares necesarios si los enlaces entre primarias y secundarias
se establecen con sistemas TAT(12+12).
Utilice la aproximación: B(c,u) = 0.012 u/c
Página 3 de 7
Tema 3
PROBLEMA 4
Considere de nuevo la figura del problema anterior. Considere igualmente que las rutas
finales se han dimensionado en base a una probabilidad de pérdida del 1% y las
secciones directas con una probabilidad de desbordamiento del 10%.
La duración de las llamadas puede aproximarse por la ley exponencial-negativa. Se
estima que todas las llamadas de salida de la central A tienen el mismo tiempo de
duración (tiempo medio de duración de una llamada) y que la probabilidad de que la
duración de cualquiera de ellas sea mayor o igual a 5 minutos es del 8.2085%.
a) Rutas posibles desde E con destino A, indicadas por orden de prioridad según
las normas de encaminamiento.
b) Tráfico desbordado en la central B.
c) Tráfico ofrecido y cursado por la sección directa C → E en la hora cargada.
d) Duración media de llamadas salientes en la central A.
e) Tráfico total de salida en HC en la central A y número de intentos de llamadas
salientes en la misma.
PROBLEMA 5
La figura representa parte de la estructura de una región telefónica junto al tráfico
intercambiado en la HC por las distintas centrales. Las rutas finales se han
dimensionado en base a una probabilidad de pérdida del 1% y las secciones directas con
una probabilidad de desbordamiento del 10%.
Calcule el tráfico ofrecido al tramo C→D.
Página 4 de 7
Tema 3
PROBLEMA 6
La figura muestra una alternativa de ruta entre 2 abonados telefónicos, para la que se
estiman las probabilidades de bloqueo pci y pRi. Calcular la probabilidad de fallo en la
llamada.
pci = p R2 = 0.01
p R1 = pR3 = 0.02
PROBLEMA 7
Página 5 de 7
Tema 3
SOLUCIONES A LOS PROBLEMAS
PROBLEMA 1
PROBLEMA 2
PROBLEMA 3
a) Ruta directa: ABHK
Ruta alternativa 1: ABCEHK
Ruta final: ABCDEHK
b) TA →sector H = 2E
c) TA →prov E = 4E
Página 6 de 7
Tema 3
d) TO B→H = 7E
e) TO B→E = 8E
f) TDB = 1.5E
g) 1º. TO B→C = 86.5E
2º. TCB→C = 0.99*TOB→C = 85.635E
3º. c=104 circuitos
4º. Nº de haces de 12 ctos/haz → 10 haces
PROBLEMA 4
a) Ruta directa: EBA
Ruta final: EDCBA
b) TDB = 1.5E coincide con apartado f del problema anterior.
c) TOC→E = 46.5E
TCC→E = 0.9 *TOC→E = 41.85E
d)
1 = 2 minutos
µ
e) 34 Erlangs
1020 llamadas
PROBLEMA 5
TOC→D = 104.65E
PROBLEMA 6
Pr {éxito} = 0.99 × 0.98 = 0.9133
Pr {fallo} = 1 − Pr {éxito} = 8.67%
Pr {éxito} = 0.99 × 0.98 = 0.9133
Pr {fallo} = 1 − Pr {éxito} = 8.67%
5
2
5
2
Página 7 de 7