Diseño de Contadores Síncronos con flip flops. Documento escrito

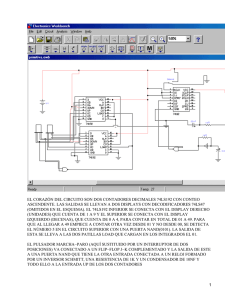
Diseño de contadores síncronos.
Por jcrls.
Para comenzar, debes tener en cuenta que la principal característica de estos contadores radica en la conexión
del reloj a todos los flip flops al mismo tiempo. En los asíncronos, la señal de reloj se propaga en cascada entre
los flip flops.
A partir de las tablas de funcionamiento de cada flip flop, es posible obtener las propias de excitación, las cuales
son fundamentales para el diseño asíncrono.
Dividiremos este documento en dos aproximaciones: diseño síncrono sin variables de control y diseño síncrono
con variables de control de dirección.
Contadores síncronos sin variable adicional de control.
La primera aproximación se refiere a contadores cuya única condición de conteo radica en el pulso de reloj; es
decir, sólo esperan por un cambio en la señal de reloj para pasar al estado siguiente y mantener una dirección
determinada.
Considérese el diseño de un contador descendente de números primos de 3 bits. Utilizaremos flip flops J-K para
nuestra solución. A continuación se aprecian las tablas de funcionamiento y de excitación del flip flop en
cuestión.
Tabla de funcionamiento del flip flop J-K
J
K
Q
Q+
0
0
0
0
0
0
1
1
0
1
0
0
0
1
1
0
1
0
0
1
1
0
1
1
1
1
0
1
1
1
1
0
Tabla de excitación del flip flop J- K
Q
Q+
J
K
0
0
0
X
0
1
1
X
1
0
X
1
1
1
X
0
El diagrama de estados propuesto es el siguiente. Obsérvese que la única condición de cambio es el pulso de
reloj y estamos regresando al estado 0 (000) después del estado 1 (001); idealmente no debería pasar por cero,
más que al iniciar la máquina de estados.
La tabla que resuelve el diseño es la siguiente. C, B y A son los estados presentes en orden de significancia.
Debido a que no se tiene ninguna condición que controle la dirección del conteo (siempre es descendente), se
utiliza la misma columna de estados presentes para determinar los estados siguientes.
De acuerdo a la tabla de excitación y refiriéndonos exclusivamente al flip flop C tenemos que la primera
combinación determina pasar de 0 a 1, por lo que JC tendrá 1 y KC una condición don’t care; tal y como se
aprecia con la flecha indicada en la misma tabla.
C
0
1
1
0
0
0
Estados presentes
B
A
0
0
1
1
0
1
1
1
1
0
0
1
JC
1
X
X
0
0
0
KC
X
0
1
X
X
X
Flip flops J-K
JB
KB
1
X
X
1
1
X
X
0
X
1
0
X
JA
1
X
X
X
1
X
KA
X
0
0
1
X
1
Los mapas que entregan las ecuaciones son los siguientes. Existen algunos estados (4 y 6) que no son parte de
la solución, por lo que se consideran como don’t care y se indican de diferente color.
00
0
1
A
1
0
JC = B’A’
00
0
1
A
1
0
JB = A’ + C
0
A
1
JA = 1
00
1
X
CB
01
X
X
CB
01
0
0
11
X
X
10
X
X
CB
01
X
X
11
X
X
10
X
1
CB
00
01
0
X
1
A
1
X
0
KB = A’ + C
CB
01
1
X
11
X
X
10
X
X
00
X
1
00
0
X
A
1
X
KC = B’
0
A
1
KA = C’
CB
01
X
1
11
X
0
10
X
1
11
X
1
10
X
X
11
X
0
10
X
0
Finalmente, las ecuaciones obtenidas son las siguientes. El apóstrofe después de una variable indica negación.
JC = B’A’
KC = B’
JB = A’ + C
KB = A’ + C
JA = 1
KA = C’
El siguiente diagrama fue capturado y simulado en CircuitMaker. Los flip flops utilizados son J-K, 74LS112.
Contadores síncronos con una variable adicional de control
Para un diseño con una variable que permita controlar la dirección del conteo (ascendente o descendente), es
necesario considerar una tabla con n flip flops más la variable mencionada. Como ejemplo diseñaremos un
contador de 3 bits, que de manera ascendente muestre números pares y de manera descendente números
primos. En la tabla, la variable “p” permite el cambio en el sentido del conteo. Los flip flops a utilizar serán de
tipo “T”.
El diagrama de estados que cumple el conteo es el siguiente. Obsérvese que cuando la variable de control “p” es
0, el conteo es ascendente; y cuando p = 1, será descendente. La señal de reloj se obvia para pasar de un estado
a otro. En el conteo descendente de números primos, no se regresa al estado 0; es decir, no se considera el 0
como número primo.
Para escribir la tabla de funcionamiento del contador completo, es obligatorio considerar la variable adicional
que controla la dirección del conteo. En la tabla siguiente, C es el flip flop más significativo y A es el menos
significativo.
Estados presentes
C
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
A
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
p
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Estados
siguientes
C
B
A
0
1
0
1
1
1
0
1
0
1
1
1
1
0
0
0
0
1
1
0
0
0
1
0
1
1
0
0
1
1
1
1
0
0
1
1
0
0
0
1
0
1
0
0
0
1
0
1
Para obtener los datos de excitación del flip flop en cuestión, es posible aplicar dos mecanismos de búsqueda:
horizontal y vertical. Cualquiera de ambas búsquedas es válida; aunque visiblemente, la primera técnica deriva
en ecuaciones más reducidas que la segunda. Además, cuando se trabaja con la búsqueda vertical posiblemente
se requiera forzar al circuito con un reset para comenzar un conteo lógico (no siempre es necesario).
La búsqueda horizontal permite obtener la tabla de los flip flops comparando directamente el bit del estado
presente contra el estado siguiente, como lo indican las flechas marcadas en la tabla siguiente. Recuerda que el
flip flop utilizado es de tipo T.
Tabla de funcionamiento del flip flop tipo T
T
Q
Q+
0
0
0
0
1
1
1
0
1
1
1
0
Tabla de excitación del flip flop tipo T
Q
Q+
T
0
0
0
0
1
1
1
0
1
1
1
0
De acuerdo a la columna de la variable C, en la primera combinación se aprecia que cuando el conteo es
ascendente con p = 0, pasaremos de un estado presente 0 a un estado siguiente 0, con respecto a una linealidad
horizontal.
Estados presentes
C
0
0
0
0
B
0
0
0
0
A
0
0
1
1
P
0
1
0
1
Estados
siguientes
C
B
A
0
1
0
1
1
1
0
1
0
1
1
1
Flip Flops T
TC
0
1
0
1
TB
1
1
1
1
TA
0
1
1
0
0
0
0
0
1
1
1
1
1
1
1
1
1
1
1
1
0
0
0
0
1
1
1
1
0
0
1
1
0
0
1
1
0
0
1
1
0
1
0
1
0
1
0
1
0
1
0
1
1
0
1
0
1
0
1
0
0
1
0
1
0
0
0
1
1
1
1
1
0
0
0
0
0
1
0
0
0
1
0
1
0
1
0
1
1
0
1
0
0
1
0
1
1
0
1
0
1
1
1
0
1
1
1
1
1
1
1
1
0
1
1
1
0
1
1
0
0
1
1
0
Los resultados de los mapas de Karnaugh son:
TC = B $ p
TB = C + B’ + A’ + p’
TA = A $ p + (C’BA)
El caracter $ representa el operador xor.
Para la búsqueda vertical, sólo se utilizan los estados siguientes de C, B y A. La comparación se realiza de
acuerdo a la flecha dibujada.
Estados presentes
C
0
0
0
0
0
0
0
0
1
1
1
1
1
1
1
1
B
0
0
0
0
1
1
1
1
0
0
0
0
1
1
1
1
A
0
0
1
1
0
0
1
1
0
0
1
1
0
0
1
1
P
0
1
0
1
0
1
0
1
0
1
0
1
0
1
0
1
Estados
siguientes
C
B
A
0
1
0
1
1
1
0
1
0
1
1
1
1
0
0
0
0
1
1
0
0
0
1
0
1
1
0
0
1
1
1
1
0
0
1
1
0
0
0
1
0
1
0
0
0
1
0
1
Flip Flops T
TC
1
1
1
0
1
1
1
1
1
1
1
0
1
1
1
1
TB
0
0
0
1
0
0
1
0
0
0
0
1
0
0
0
1
TA
1
1
1
1
1
1
0
0
1
1
1
1
1
1
1
1
Los resultados de los mapas de Karnaugh son:
TC = A’ + B + p
TB = A (B’p + Cp + C’Bp’)
TA = A’ + C + B’
También es recomendable realizar el diseño con otros flip flops, buscando el circuito mínimo a alambrar. Con flip
– flops tipo D, obtienes las siguientes ecuaciones a través de la búsqueda vertical:
DC = C’A’p + Bp + C
DB = B’ (C + A’ + p’)
DA = p (A’ + B + C)
Si lo realizas con J-K, obtienes las siguientes ecuaciones.
JC = KC = B $ p
JB = 1
KB = p’ + (C $ A)’
JA = p
KA = p’+ C’B
El caracter $ representa una operación xor. JC y KC son iguales, JB se conecta a Vcc, KB contiene una
operación xor negada, JA y KA son complementos entre sí.
Juan Carlos Herrera Lozada, [email protected]
CIDETEC IPN, México