Leer Texto.

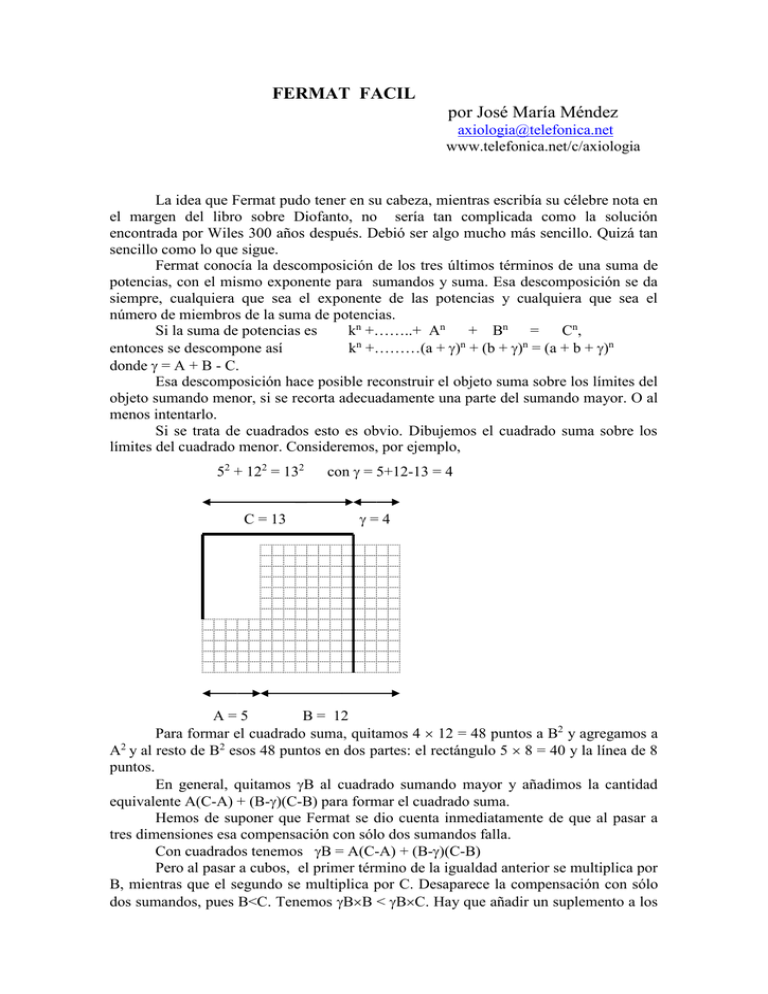
FERMAT FACIL
por José María Méndez
[email protected]
www.telefonica.net/c/axiologia
La idea que Fermat pudo tener en su cabeza, mientras escribía su célebre nota en
el margen del libro sobre Diofanto, no sería tan complicada como la solución
encontrada por Wiles 300 años después. Debió ser algo mucho más sencillo. Quizá tan
sencillo como lo que sigue.
Fermat conocía la descomposición de los tres últimos términos de una suma de
potencias, con el mismo exponente para sumandos y suma. Esa descomposición se da
siempre, cualquiera que sea el exponente de las potencias y cualquiera que sea el
número de miembros de la suma de potencias.
Si la suma de potencias es
kn +……..+ An
+ Bn = Cn,
entonces se descompone así
kn +………(a + )n + (b + )n = (a + b + )n
donde  = A + B - C.
Esa descomposición hace posible reconstruir el objeto suma sobre los límites del
objeto sumando menor, si se recorta adecuadamente una parte del sumando mayor. O al
menos intentarlo.
Si se trata de cuadrados esto es obvio. Dibujemos el cuadrado suma sobre los
límites del cuadrado menor. Consideremos, por ejemplo,
52 + 122 = 132
C = 13
con  = 5+12-13 = 4
=4
A=5
B = 12
Para formar el cuadrado suma, quitamos 4  12 = 48 puntos a B2 y agregamos a
2
A y al resto de B2 esos 48 puntos en dos partes: el rectángulo 5  8 = 40 y la línea de 8
puntos.
En general, quitamos B al cuadrado sumando mayor y añadimos la cantidad
equivalente A(C-A) + (B-)(C-B) para formar el cuadrado suma.
Hemos de suponer que Fermat se dio cuenta inmediatamente de que al pasar a
tres dimensiones esa compensación con sólo dos sumandos falla.
Con cuadrados tenemos B = A(C-A) + (B-)(C-B)
Pero al pasar a cubos, el primer término de la igualdad anterior se multiplica por
B, mientras que el segundo se multiplica por C. Desaparece la compensación con sólo
dos sumandos, pues B<C. Tenemos BB < BC. Hay que añadir un suplemento a los
dos sumandos cubos para lograr una compensación nueva y distinta, como en el
ejemplo que sigue donde superficie FC < B2.
En este caso mínimo ese suplemento es sólo un tercer cubo:
23 + 123 + 163 = 183
con  = 10
Recortemos en 163 para reconstruir la suma 183 sobre los límites de 123.
18
F
12
16
18
El recorte en 163 es 10.16.16 = 2560 (B2)
Con eso habría que rellenar:
Volumen sobre F (FC)
[(12.6) + (6.2)] 18 = 1512
Vacío sobre 123
12.12.6
= 864
2
Vacío sobre parte no recortada 16
6.16.2
= 192
Total
2568
3
Obviamente hacen falta además las 8 unidades del suplemento 2 .
Cabe también que la nueva compensación exija más de un cubo, como en
23 + 33 + 83 + 133 = 143
con  = 7
Si pasamos a cuartas potencias, el suplemento puede exigir tres
sumandos como en
14 + 24 +124 + 244 + 444 = 454
con  = 23
Pero en el caso de Elkies el suplemento es un solo sumando:
958004 + 2175194 + 4145604 = 4224814
con  = 209598
No se explica bien por qué los matemáticos se obsesionasen tanto y por tanto
tiempo, siguiendo ciegamente a Descartes y despreciando a Euclides. Descartes abrió la
puerta a los grandes adelantos técnicos que nos han proporcionado las matemáticas
desconectadas de la geometría. Pero el castigo ha sido tener delante algo tan simple
como lo anterior delante de los ojos y no verlo durante 300 años.
Regla para la descomposición:
Cuadrados
B = (C -A)(A -B + C)
Cubos
Suplemento + B2 = (C -A)(A2 -B2 + C2 +AC)
4ª potencias
Suplemento + B3 = (C -A)(A3 -B3 + C3 + A2C + AC2)