tarea 04 - Liceo Emperadores Aztecas

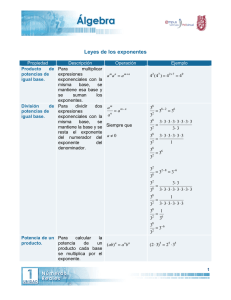
TAREA 04
Productos y cocientes de potencias
Leyes de los exponentes
Leyes de los exponentes
La introducción de la notación de exponentes “x” se le atribuyó al matemático y filósofo
francés René Descartes (1596-1650). Dicha notación, así como otros progresos en álgebra,
se encontraron en su famoso libro Geometría, publicado en 1637.
El producto de varios factores iguales recibe el nombre de potencia.
Se llama base el número que se repite como factor y el exponente, el número que nos indica
cuántos factores iguales hay.
Ejemplos:
32  3 x 3  9
3 es la base y 2 es el exponente.
 53   5 5 5   125
- 5 es la base y 3 es el exponente.
a 4  a a a a
a es la base y 4 es el exponente.
En general, si a es un número racional cualquiera, y n es un número natural mayor que 1.
a n  a a a ...a
n factores
a es la base y n es el exponente.
Todo número racional con exponente 1 es igual a sí mismo.
a1  a
Todo número racional no nulo (distinto de cero) con exponente 0 es igual a 1.
a0  1
0
La expresión 0 no está definida.
De acuerdo con la regla de los signos de la multiplicación, las potencias de números
positivos son siempre positivas, y las potencias de números negativos pueden ser positivas
o negativas. Son positivas si el exponente es par, y negativas si el exponente es impar.
Ejemplos:
1.
Escribir en forma de producto la potencia que en cada caso se indica:
4
3
 3  3  3  3 
m3  m  m  m
a)
b)
       
4
 4  4  4  4 
c)
 25   2 2 2 2 2
d)
a  bx
 a  b a  b ...a  b 
x factores
2. Escribir en forma de potencia los siguientes productos:
a)
x x x x  x 4
c)
 1  1  1  1   1 
            
 2  2  2  2   2 
e)
a a a ...a  a b
b factores
b)
 a a a   a3
d)
m nm nm n  m n3
f)
x  yx  y...x  y  x  ys
4
s
factores
3. Calcular en cada caso la potencia que se indica:
a)
43
d)
 26
 64
 64
5
b)
 32
e)
 1.22
9
 1.44
c)
1
 1
   
2
32


f)
33
 27
Ejercicios.
A.
B.
Escribe en forma de producto las siguientes potencias:
3
a)
4
 
5
e)
 m4
4
b)
 2
 
 3
f)
c dm
c)
d)
70
Escribe en forma de potencia los siguientes productos:
a)
d)
 m m m
5 x 5 x 5...x 5
12 factores
b)
 2  2  2  2 
    
 5  5  5  5 
e)
z  z  z...z
x factores
Leyes de los exponentes enteros y positivos.
1.
a5
Producto de dos potencias de la misma base.
Ejemplos:
c)
f)
  a   a 



 b  b 
r  sr  s...r  s
20 factores
3 factores 4 factores
3
4
3 x 3  3x3x3 x 3x3x3x3
7 factores
3 3 4  3 7
3 factores
53 x 52 
2 factores
5x5x5 x 5x5
5 factores
3
5 2  5 5
2 factores
2
3 factores
3
2 2
22
 2  2  2 
         x    
3 3
33
 3  3  3 
5 factores
2 3
5
2
2
 
 
3
3
a 3  a 2  aaa aa  a 32  a 5
b 3b 4  bbb bbbb  b 34  b 7
(Primera Ley)
El producto de dos potencias de la misma base (distinta de cero es igual a la
base elevada a la suma de los exponentes.
Ejemplos:
1.
a 3 a 4  a 3 4  a 7
2.
4
5
4 5
9
b b
b
b
 
     
c c
c
c
3.
x 4 x  x 4 1  x 5
4.
y3 y2  y3  2  y5
5.
a x a y  a xy
Ejercicio:
3
a)
45 x 42
b)
3 3
   
5 5
d)
a 3a
e)
x a xb
2
c)
m5 m2
f)
m3 m a