Problema. Un pelotero de grandes ligas batea una pelota de modo

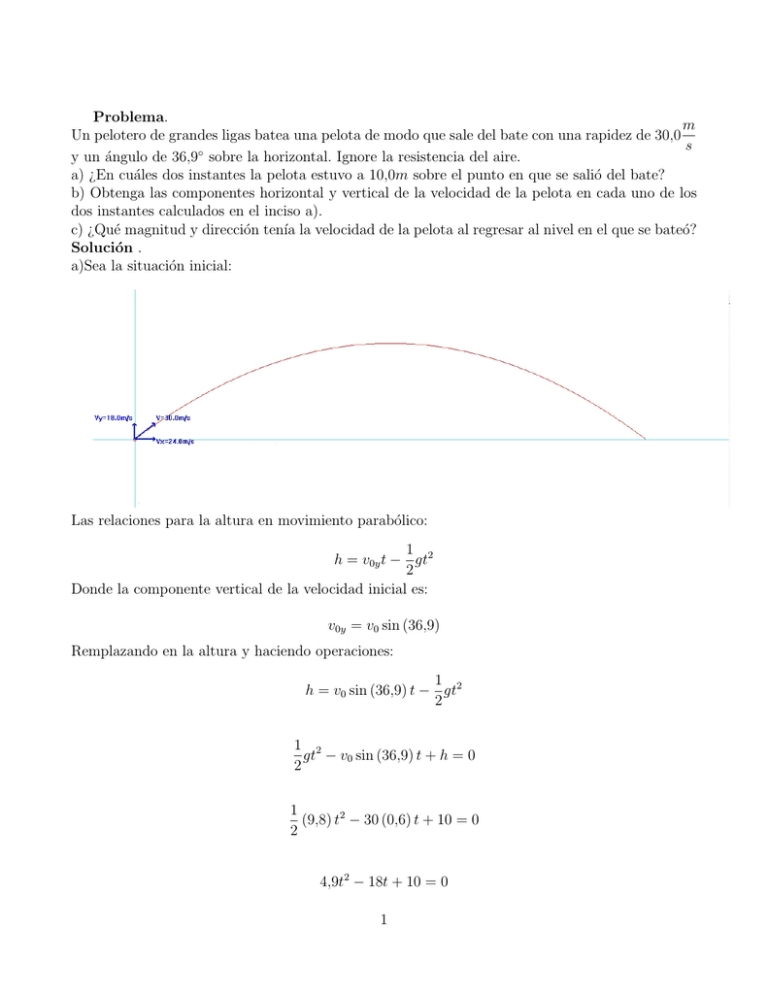
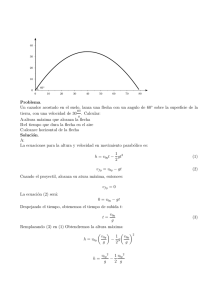
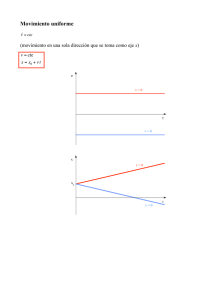
Problema.
m
Un pelotero de grandes ligas batea una pelota de modo que sale del bate con una rapidez de 30,0
s
y un ángulo de 36,9◦ sobre la horizontal. Ignore la resistencia del aire.
a) ¿En cuáles dos instantes la pelota estuvo a 10,0m sobre el punto en que se salió del bate?
b) Obtenga las componentes horizontal y vertical de la velocidad de la pelota en cada uno de los
dos instantes calculados en el inciso a).
c) ¿Qué magnitud y dirección tenı́a la velocidad de la pelota al regresar al nivel en el que se bateó?
Solución .
a)Sea la situación inicial:
Las relaciones para la altura en movimiento parabólico:
1
h = v0y t − gt2
2
Donde la componente vertical de la velocidad inicial es:
v0y = v0 sin (36,9)
Remplazando en la altura y haciendo operaciones:
1
h = v0 sin (36,9) t − gt2
2
1 2
gt − v0 sin (36,9) t + h = 0
2
1
(9,8) t2 − 30 (0,6) t + 10 = 0
2
4,9t2 − 18t + 10 = 0
1
t=
−b ±
√
b2 − 4ac
2a
a = 4,9
b = −18
c = −10
− (−18) ±
q
(−18)2 − 4 (4,9) (10)
t=
2 (4,9)
t=
18 ± 11,31
9,8
18 − 11,31
9,8
18 + 11,31
t2 =
9,8
t1 =
t1 = 0,68s
t2 = 2,99s
b)
La Componente vertical final de la velocidad:
vf y = v0y − gt2
En donde:
v0y = v0 sin (36,9)
vf y = v0 sin (36,9) − gt
Remplazando los tiempos del inciso a):
vf y = v0 sin (36,9) − gt1
vf y = v0 sin (36,9) − gt2
2
vf y = 30 sin (36,9) − 9,8 (0,68)
vf y = 30 sin (36,9) − 9,8 (2,99)
m
s
m
= −11,29
s
vf y = 11,3
vf y
Como se aprecia en las figuras, para el tiempo t1 :
para el tiempo t2
c)
Para determinar la magnitud, primero calcular el tiempo de vuelo:
La velocidad final vertical en cualquier momento es:
vf y = v0y − gt
3
Cando el movil llega a su punto más alto, entonces la velocidad final de la componente vertical es:
vf y = 0
Por tanto:
0 = v0y − gt
Despejar t, es el tiempo de subida ts :
ts =
v0y
g
El tiempo de vuelo tv es:
tv = 2ts
tv = 2
v0y
g
v0y = v0 sin (36,9)
tv = 2
v0 sin (36,9)
g
La componentes de la velocidad para el tiempo de vuelo son:
vf x = v0x = v0 cos (36,9)
vf y = v0y − gtv
vf y = v0 sin (36,9) − g2
v0 sin (36,9)
g
vf y = v0 sin (36,9) − 2v0 sin (36,9)
4
vf y = −v0 sin (36,9)
El módulo dela velocidad es:
v=
p
vf x 2 + vf y 2
q
v = (v0 cos (36,9))2 + (−v0 sin (36,9))2
v=
v=
q
v0 2 cos2 (36,9) + v0 2 sin2 (36,9)
q
v0 2 cos2 (36,9) + sin2 (36,9)
Por las relaciones de identidad trigonométricas:
cos2 (36,9) + sin2 (36,9) = 1
v=
p
v0 2
v = v0
El Módulo, magnitud o tamaño es el mismo que el de la velocidad inicial.
La dirección es la tangente a la trayectoria, como se observa en la figura.
El sentido está dado por el sigo de la componente final de la velocidad vertical. en vectores serı́a:
vf x = v0 cos (36,9)
vf y = −v0 sin (36,9)
El vector velocidad:
v = vf xy~i − vf y~j
5
Tal como se aprecia en la figura:
6