Hoja de problemas Tema 7

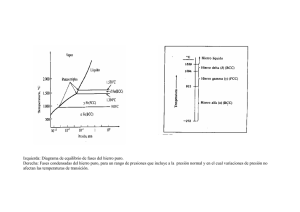
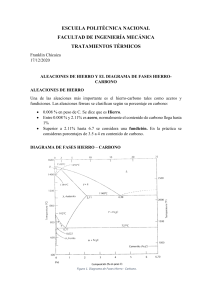
Hoja 7
FUNDAMENTOS DE CIENCIA DE MATERIALES
1
Hoja de problemas
Tema 7
1. Sea el diagrama de fases esquemático de la figura para el sistema A-B. Indique la posición de
las líneas de liquidus, solidus y solvus.
(a) Dibuje esquemáticamente las curvas de energía libre de Gibbs G versus
composición correspondientes a las temperaturas de 1500 ºC, 1300 ºC, 1000 ºC y
500 ºC.
(b) Dibuje esquemáticamente las curvas de enfriamiento para aleaciones de
composición 90 %A y 50 %A desde una temperatura de 1500 ºC hasta una
temperatura de 500 ºC. Muestre esquemáticamente la evolución de la
microestructura de dichas aleaciones en el mismo rango de temperaturas.
(c) Explicar cómo cambiaría el diagrama de fases si la energía de Gibbs de la fase
líquida fuera significativamente menor.
2. Para el sistema MgO-FeO, los extremos puros de composición, es decir, los compuestos MgO
y FeO tienen la misma estructura cristalina (igual a la estructura cristalina del NaCl), con
parámetros de red a de 0.4213 nm (MgO) y 0.4307 nm (FeO). La siguiente tabla recoge los
valores del parámetro de red a (obtenidos mediante la técnica de Rayos X) para varias
soluciones sólidas de MgO-FeO en equilibrio con un líquido en función de la temperatura.
Suponiendo que el valor del parámetro de red es proporcional a la composición, determinar
las composiciones de las soluciones sólidas en equilibrio con el líquido a cada temperatura y
dibujar esquemáticamente el diagrama de fases del sistema.
Hoja 7
FUNDAMENTOS DE CIENCIA DE MATERIALES
Composición del líquido
%Mol MgO
0
20
40
60
80
100
Temperatura
(ºC)
1350
1900
2200
2500
2700
2800
2
Solución Sólida
Parámetro de red, a (nm)
%Mol MgO
0.4307
0
0.4253
0.4235
0.4222
0.4217
0.4213
100
La siguiente figura muestra las curvas de energía libre de Gibbs de las fases líquido y sólido
del sistema MgO-FeO en función de la composición ( %Mol) a una temperatura determinada.
Por comparación con el diagrama de fases deducido en el apartado anterior, determinar la
temperatura a la que corresponde esta figura.
3. Considere un hipotético diagrama de fases de los metales A y B similar al del Sn-Pb.
Suponiendo que: (1) las fases α y β existen en los extremos A y B del diagrama,
respectivamente, (2) la composición (en peso) del eutéctico es 36% A- 64% B y (3) la
composición (en peso) de la fase α a la temperatura eutéctica es de 88% A-12% B.
Determinar la composición de la aleación cuyas fracciones de masas β primaria y β total son
0’367 y 0’768, respectivamente.
4. Considere 1’5 kg de acero al carbono con un 0’3% C (en peso), enfriados hasta temperatura
justo inferior a la eutectoide.
(a) ¿Cuántos kg de ferrita proeutectoide se forman?
(b) ¿Cuántos kg de ferrita eutectoide se forman?
(c) ¿Cuántos kg de cementita se forman?
Hoja 7
FUNDAMENTOS DE CIENCIA DE MATERIALES
3
5. La fracción másica de cementita eutectoide en un acero es 0’109. ¿Es posible determinar, con
este dato, la composición del acero? ¿Cuál es? Si no es posible, justifique por qué.
6. Enfriar hasta temperaturas inferiores a 727ºC 3,5 kg de austenita con 0,95% C en peso.
(a)
(b)
(c)
(d)
¿Cuál es la fase proeutectoide?
¿Cuántos kilogramos de ferrita y de fase proeutectoide se forman?
¿Cuántos kilogramos de perlita se forman?
Esquematizar y designar la microestructura resultante.
7. En un acero de composición 99,65% Fe y 0,35% C (en peso) a temperatura muy próxima e
inferior al eutectoide, determinar:
(a) Las fracciones de las fases ferrita y cementita.
(b) Las fracciones de ferrita proeutectoide y perlita.
(c) La fracción de ferrita eutectoide.
8. Considere el diagrama de fases correspondiente a las aleaciones entre el estaño y el plomo.
Sea una aleación Pb-Sn, con un 40% en peso de Sn a 150 ºC.
(a) ¿Qué fases presenta?
(b) ¿Cuáles son las composiciones de cada fase?
(c) Calcular la fracción en masa y la fracción en volumen de cada una de las fases
(Suponer que las densidades de α y β son 11.200 kg/m3 y 7.300 kg/m3,
respectivamente)
9. La fracción másica de ferrita eutectoide es 0,71. ¿Es posible determinar, con ese dato, la
composición del acero? ¿Cuál es? Si no es posible, justificarlo.
Hoja 7
FUNDAMENTOS DE CIENCIA DE MATERIALES
4
10. Considere una aleacion de Sn-Pb de 1,5kg que justo por encima de la temperatura eutectoide
tiene una fracción másica de fase α sólida de 0,15. Suponga que calentamos la aleación hasta
350ºC y le añadimos 1,5 kg de una aleación de Sn-Pb con 85 % de Sn. Determinar:
(a) La evolución de la microestructura resultante al enfriar muy lentamente la aleación
justo por debajo de la temperatura eutéctica.
(b) Las fases presentes y su fracción en peso.
Soluciones:
3. C=75 %B.
4. (a) 0,94 kg de ferrita proeutectoide (αproeutectoide)
(b) 0,49 kg de ferrita eutectoide (αeutectoide)
(c) 0,06 kg de cementita Fe3C
5. No, ya que el acero podría ser hipoeutectoide o hipereutectoide
6. (a) Cementita Fe3C
(b) En total, se forman 3,01 kg de ferrita α y 0,49 kg de cementita Fe3C,
de los cuales 0.11 kg corresponden a Fe3C proeutectoide y 0,38 kg
corresponden a Fe3C eutectoide.
(c) 3,39 kg de perlita
7. (a) fα=0,95
fFe3C=0,05
(b) fα proeutéctica=0,56
fperlita=0,44
(c) fα eutéctica= 0,39
8. (a) Fases α y β.
(b) Cα =11% Sn
Cβ =99% Sn
(c) fα másica= 0,67
fβ másica= 0,33
fα volumen= 0,57
fβ volumen= 0,43
9. No, ya que el acero podría ser hipoeutectoide o hipereutectoide
10. (a) C=70,25 %
(b) La microestructura consiste en granos de β primario embebidos en un
microconstituyente eutéctico (formado por láminas de α y β)
(c) fβ primario= 0,235
feutectico = 0,765
fα total=0,35
fβ total=0,65