3. movimiento en dos y tres dimensiones

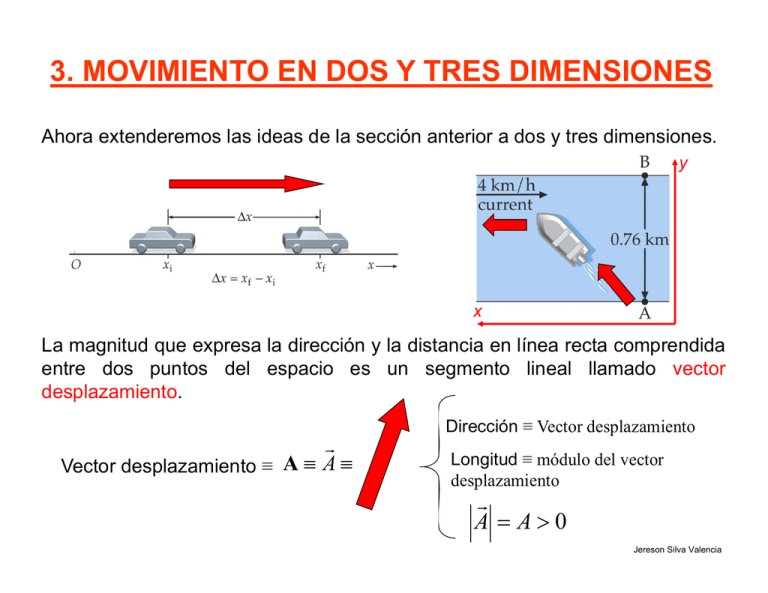
3. MOVIMIENTO EN DOS Y TRES DIMENSIONES
Ahora extenderemos las ideas de la sección anterior a dos y tres dimensiones.
y
x
La magnitud que expresa la dirección y la distancia en línea recta comprendida
entre dos puntos del espacio es un segmento lineal llamado vector
desplazamiento.

Vector desplazamiento ≡ A  A 
Dirección ≡ Vector desplazamiento
Longitud ≡ módulo del vector
desplazamiento

A  A0
Jereson Silva Valencia
El desplazamiento resultante de P1 a
P3, llamado C, es la suma de los dos
desplazamientos sucesivos A y B :
  
C  A B
Suma de vectores desplazamientos :
Jereson Silva V.
Propiedades Generales de los Vectores.
“Los vectores son magnitudes con módulo, dirección y sentido que
se suman como los desplazamientos”.
Las magnitudes que carecen de dirección asociada se denominan
escalares.
Dirección ≡ dirección del Vector

Vector ≡ A  A 
Longitud ≡ proporcional al módulo del vector
A. Igualdad entre vectores

A A

BB
 
AB
Jereson Silva Valencia
B. Producto de un vector por un escalar


B  sA

A A


B  2A 
C. Resta de vectores
Para restar el vector B del vector A basta sumarle –B:
 
 
 

C  A  B  A B
Jereson Silva Valencia
D. Componentes de los vectores
La componente de un vector a lo largo de una línea en el espacio es la
longitud de la proyección del vector sobre dicha línea. Se obtiene trazando
una línea perpendicular desde el extremo o flecha de un vector a la línea.
Componentes rectangulares:
Si conocemos Ax y Ay podemos obtener el
ángulo 
tan  
Ay
Ax
  arcotan
,
Ay
Ax
El módulo de A es
A A  A
2
x
2
y
Jereson Silva Valencia
C x  Ax  Bx
C y  Ay  B y
Rx  Ax  Bx
R y  Ay  B y
Jereson Silva Valencia
Jereson Silva Valencia
Ejemplo 1: Suponga que usted trabaja como animador en un centro turístico
en un a isla tropical. Dispone de un mapa que le indica las direcciones a
seguir para enterrar un tesoro en un lugar determinado. Usted no desea
malgastar el tiempo dando vueltas por la isla, porque quiere acabar pronto
para ir a la playa y hacer surfing. Las instrucciones son ir 3 km hacia el
oeste y luego 4 km en la dirección de 60° al nordeste. ¿En qué dirección
debe moverse y cuánto tendrá que caminar para cumplir su objetivo con la
máxima rapidez?
Vectores unitarios:
Un vector unitario es un vector sin dimensiones de módulo unidad.

A A

aˆ  A A 
1




A  Ax i  Ay j  Az k
Jereson Silva Valencia
Posición, Velocidad y Aceleración.
El vector posición de una partícula es un vector trazado desde el origen de
un sistema de coordenadas hasta la posición de la partícula. Para un punto
(x,y) su vector posición r es
 

r  xi  yj
El cambio de posición de
la partícula es el vector
desplazamiento r:
  
r  r2  r1
Jereson Silva Valencia
El cociente entre el vector desplazamiento y el intervalo de tiempo t = t2 – t1
es el vector velocidad media.

 r
v m
t
Definimos el vector velocidad
instantánea como el límite del
vector velocidad media cuando t
tiende a cero:
 

Δr dr
v = lim
=
Δt0 Δt
dt


 dx  dy 
v i
j  vx i  v y j
dt
dt
Jereson Silva Valencia
Ejemplo 2: Un barco de vela tiene las coordenadas (x1, y1)=(110 m, 218 m)
en el instante t1=60 s. Dos minutos más tarde, en el instante t2, sus
coordenadas son (x2 , y2)=(130 m, 205 m). Determinar la velocidad media
en este intervalo de dos minutos.
Jereson Silva Valencia
Velocidad relativa
Si una partícula se mueve con
velocidad VpA relativa a un
sistema de coordenadas A, y
éste a su vez se mueve con
velocidad VAB relativa a otro
sistema B, la velocidad de la
partícula respecto a B es



V pB  V pA  VAB
Jereson Silva Valencia
Se define el vector aceleración media como el cociente entre la variación del
vector velocidad instantánea v y el intervalo de tiempo t:


v
am 
t
El vector aceleración instantánea es la derivada del vector velocidad respecto
al tiempo



v dv
a  lim

t 0 t
dt
También tenemos
2 
2
2 




dv
 dvx
d z
dvz
d x
d y
y
k = 2 i + 2 j+ 2 k
j+
a=
i+
dt
dt
dt
dt
dt
dt



= ax i + a y j + az k
Jereson Silva Valencia
Ejemplo 3: La posición de una pelota de béisbol golpeada por el bateador viene
dada por la expresión r(t) = 1.5 m i +(12 m/s i + 16 m/s j) t – 4.9 m/s2 j t2.
Determinar su vector velocidad y vector aceleración.

 

r  xi  yj  zk

 dr dx  dy  dz 
v
j k
 i
dt dt
dt
dt



 vx i  v y j  vz k

 dv dv x  dv y  dv z 
a
i
j
k

dt
dt
dt
dt
d 2x  d 2 y  d 2z 
 2 i  2 j 2 k
dt
dt
dt
Jereson Silva Valencia
Ejemplo 4: Un coche se mueve hacia el este a 60 km/h. Toma una curva y 5 s
más tarde viaja hacia el norte a 60 km/h. Determinar el vector aceleración
media del coche.
Jereson Silva Valencia
Velocidad y aceleración
•
Usted lanza un objeto hacia arriba en el aire.
En el punto mas alto, el objeto tendrá:
1. Velocidad y aceleración nulas.
2. Aceleración nula pero velocidad diferente de
cero.
3. Velocidad cero y aceleración diferente de cero.
4. Velocidad y aceleración diferentes de cero.
Jereson Silva Valencia
Movimiento de Proyectiles
La figura muestra el lanzamiento de una
partícula con velocidad inicial v0 y formando
un ángulo 0 con el eje horizontal.
Las componentes de la velocidad inicial son:
v0 x  v0Cos 0
v0 y  v0 Sin 0
Las componentes de la aceleración son:
ax  0
ay  g
Para las velocidades tenemos
v x  v0 x
v y  v0 y  gt
Las componentes horizontal y vertical del movimiento de
proyectiles son independientes
Los desplazamientos x e y vienen dados por
x(t )  x0  v0 x t
;
y (t )  y0  voy t  gt
1
2
2
Jereson Silva Valencia
Ejemplo 5: Desde el tejado de un edificio de 20 m de altura se lanza una
piedra con un ángulo de tiro de 53° sobre la horizontal. Si el alcance
horizontal de la piedra es igual a la altura del edificio, con qué velocidad
se lanzó la roca?¿Cuál es la velocidad de ésta justo antes de chocar
contra el suelo?
Jereson Silva Valencia
Más sobre movimiento de proyectiles


 

a  axi  a y j   g j  g



v  vx i  v y j
 
 
 v0  gt ; v  gt
  
2
1
r  r0  v0t  2 gt
 
2
1
r  v0t  2 gt
Jereson Silva Valencia
Preguntas cuarta sesión
•
•
•
•
Definición de fuerza y método de medición
Explique la Ley de Inercia (historia)
Masa inercial y masa gravitacional
Fuerzas en la caída libre y en el tiro
parabólico
• Ejemplo de fuerzas de contacto, fuerza
eléctrica, magnética y en un resorte.
• Diagrama de las fuerzas que actúan sobre
un cuerpo en un plano inclinado.
Jereson Silva Valencia