Unas breves notas sobre las máquinas térmicas y la 2a ley.

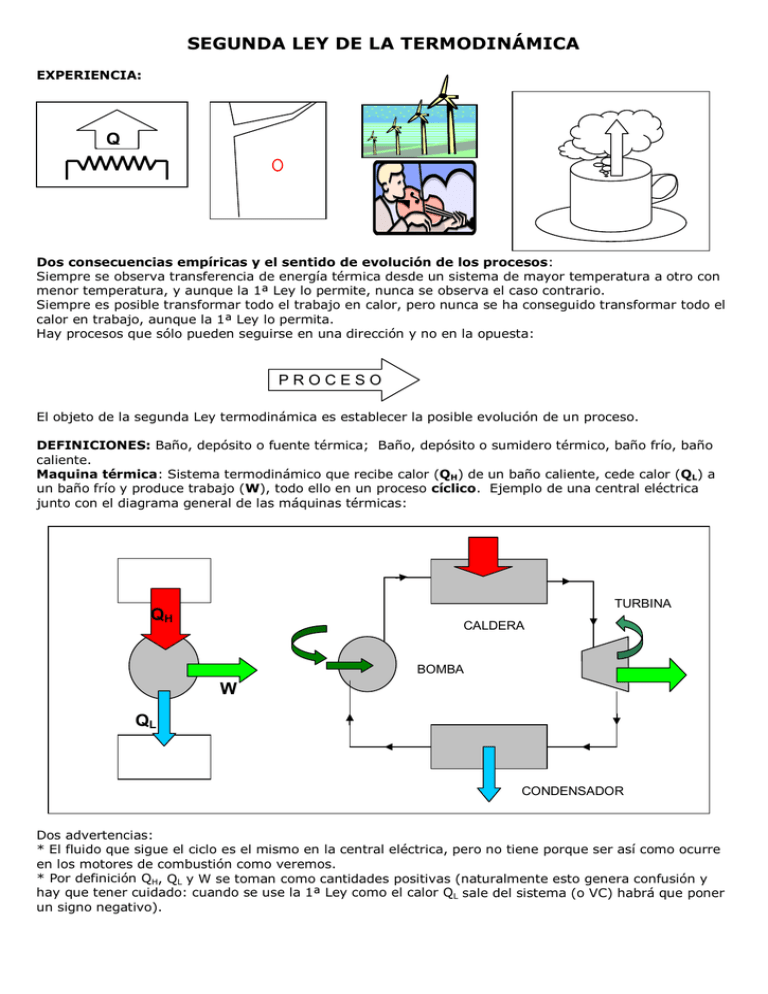
SEGUNDA LEY DE LA TERMODINÁMICA
EXPERIENCIA:
Q
Dos consecuencias empíricas y el sentido de evolución de los procesos:
Siempre se observa transferencia de energía térmica desde un sistema de mayor temperatura a otro con
menor temperatura, y aunque la 1ª Ley lo permite, nunca se observa el caso contrario.
Siempre es posible transformar todo el trabajo en calor, pero nunca se ha conseguido transformar todo el
calor en trabajo, aunque la 1ª Ley lo permita.
Hay procesos que sólo pueden seguirse en una dirección y no en la opuesta:
PROCESO
El objeto de la segunda Ley termodinámica es establecer la posible evolución de un proceso.
DEFINICIONES: Baño, depósito o fuente térmica; Baño, depósito o sumidero térmico, baño frío, baño
caliente.
Maquina térmica: Sistema termodinámico que recibe calor (QH) de un baño caliente, cede calor (QL) a
un baño frío y produce trabajo (W), todo ello en un proceso cíclico. Ejemplo de una central eléctrica
junto con el diagrama general de las máquinas térmicas:
TURBINA
QH
CALDERA
BOMBA
W
QL
CONDENSADOR
Dos advertencias:
* El fluido que sigue el ciclo es el mismo en la central eléctrica, pero no tiene porque ser así como ocurre
en los motores de combustión como veremos.
* Por definición QH, QL y W se toman como cantidades positivas (naturalmente esto genera confusión y
hay que tener cuidado: cuando se use la 1ª Ley como el calor QL sale del sistema (o VC) habrá que poner
un signo negativo).
La 1ª Ley establece que: ∆U=Q-W=QH – QL – W, como el proceso es un ciclo (∆U=0):
QH – QL = W
No todas las máquinas obtienen el mismo trabajo consumiendo el mismo calor y por tanto, se define
rendimiento o eficiencia de una máquina al cociente entre lo que se desea (trabajo) y lo que se gasta
(QH):
η = W/QH = (QH – QL)/QH = 1 – QL/QH,
que necesariamente tiene que ser η<1 (si fuera igual a 1 ⇒ QL=0 y todo el calor se ha convertido en
trabajo, algo que no ocurre nunca como hemos visto).
¿Dónde está el origen de la pérdida de energía QL?
Hay dos causas: una es debida a la fricción y que puede ser reducida en principio sin límite, es una
cuestión de técnica. Otra es inevitable y forma parte del comportamiento de la materia: la segunda ley
nos enseña a saber hasta donde podemos llegar para aumentar el rendimiento al máximo posible, que
nunca será UNO. El siguiente proceso muestra claramente la imposibilidad de eliminar todas las pérdidas
en un proceso cíclico.
W=15kJ
30ºC
90ºC
30ºC
Q=100kJ
Q=-85kJ
Baño a 100ºC
Baño a 20ºC
De lo dicho podemos concluir con el enunciado de Kelvin-Planck de la 2ª Ley:
Es imposible para cualquier máquina térmica recibir calor de un baño caliente, producir trabajo y no ceder
nada de calor a un baño frío.
REFRIGERADORES Y BOMBAS DE CALOR:
Q
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
A
EVAPORADOR
800kPa
30ºC
QH
VÁLVULA
W
QL
800kPa
60ºC
COMPRESOR
120kPa
-25ºC
120kPa
-20ºC
CONDENSADOR
Son “máquinas térmicas” usadas en la dirección opuesta: gastando trabajo, W, se saca energía de un
baño frió, QL, y se cede calor, QH, a un baño caliente. La 1ª Ley exige que W+QL=QH, es decir QH>QL
Según se utilice para enfriar el baño frío o calentar el caliente se llama refrigerador o bomba de calor
respectivamente. Los acondicionadores de aire suelen actuar de las dos formas mediante un sistema de
controles de forma que en invierno enfrían la calle para calentar la casa y en verano al revés.
Coeficientes de operación o rendimiento (NO ES LO MISMO QUE η)
COP(refrigerador)
=energía deseada/coste energético =QL/W = 1/(QH/QL – 1)
que puede ser mayor que 1.
COP(bomba de calor)=energía deseada/coste energético= QH/W = 1/(1 – QL/QH)
que es necesariamente mayor que 1
De lo dicho podemos concluir con otro enunciado de la 2ª Ley debido a Clausius:
Es imposible para cualquier máquina térmica recibir calor de un baño frío y cederlo a un baño caliente sin
gasto de trabajo.
Equivalencia entre los dos enunciados
TH
QH
QH+QL
W=QH
η=100%
QL
≡
QL
QL
TL
Movimientos perpetuos de primera y segunda especie: máquinas que violan el premier o el segundo
principio de la termodinámica.
PROCESOS REVERSIBLES E IRREVERSIBLES.
REVERSIBLES: LOS QUE SE PUEDEN VOLVER A RECORRER ESTADO A ESTADO, DEL SISTEMA Y
EL RESTO DEL UNIVERSO, EN SENTIDO OPUESTO.
IRREVERSIBLES: LOS QUE NO SON REVERSIBLES. ≡
Observaciones
• No olvide que siempre tenemos el sistema y el resto del universo.
• Ningún proceso real es reversible: caídas, roturas, mezclas, fricción, deformaciones, transferencia
de calor, ...
• La irreversibilidad suele estar ligada a la violencia del proceso y exigen mayor cantidad de trabajo
o generan menor cantidad de trabajo ¡siempre en contra nuestra! Reducen el rendimiento de
cualquier dispositivo termodinámico.
•
•
Los procesos reversibles son infinitamente lentos. El proceso pasa por sucesivos estados de
equilibrio los cuales, estrictamente, se alcanzan en un tiempo infinito.
Los procesos irreversibles también pueden ser lentos.
A
I
S
L
A
N
T
E
TH
•
TL < TH
Un sistema puede volver al estado inicial en un proceso irreversible PERO el resto del universo,
inevitablemente, ha cambiado.
P
P
SISTEMA
RESTO
UNIVERSO
•
•
•
•
•
•
•
•
V
V
En un proceso irreversible puede ocurrir que el proceso seguido por el sistema que estamos
estudiando haya pasado por sucesivos estados de equilibrio, entonces es posible recorrerlos en
sentido opuesto para volver al estado inicial (y no el resto del universo); estos procesos se llaman
internamente reversibles, el proceso sigue siendo irreversible. (El diagrama anterior es un caso de
este tipo)
En un proceso irreversible puede ocurrir que el proceso seguido por el resto del universo haya
pasado por sucesivos estados de equilibrio, entonces es posible recorrerlos en sentido opuesto
para volver al estado inicial (y no el sistema); estos procesos se llaman externamente reversibles,
el proceso sigue siendo irreversible. (Los baños suelen verificar esta condición).
Hay procesos que son a la vez internamente y externamente reversibles y aún son procesos
totalmente irreversibles. (Un ejemplo es el caso mencionado de la transferencia de energía térmica
entre dos sistemas con un aislante).
Podemos tratar de hacer los procesos “lo menos irreversibles” posible. La razón de ello es doble:
en los procesos reversibles es relativamente fácil evaluar cualquier variable termodinámica y sirven
de comparación de los sistemas reales.
El procedimiento para hacer a un proceso reversible es producir lentamente el trabajo (proceso
cuasi-estático) y disponer de muchos baños térmicos para hacer los intercambios de calor poco a
poco. Un proceso reversible necesita producir trabajo de una manera infinitamente lenta y
disponer de infinitos baños térmicos.
En principio se podría tender a mejorar los rendimientos haciendo los sistemas “más reversibles”
pero, además de los problemas técnicos, la potencia sería cada vez menor.
No olvide nunca que las propiedades de un estado termodinámico no dependen de cómo se haya
alcanzado ese estado, sea reversible o irreversiblemente.
EL CICLO DE CARNOT
Es el proceso cíclico reversible que sigue un sistema y que consiste de cuatro pasos: dos procesos
isotermos y dos procesos adiabáticos según se indica a continuación. Aunque nos referiremos a un gas, el
sistema puede ser cualquier material, incluso puede renovarse como ocurre en los motores de explosión.
Expansión isotérmica a TH ( 1  2 )
El sistema se pone en contacto con un baño caliente
de temperatura TH absorbiendo una cantidad de calor
QH mientras se expande a la temperatura del baño
y por tanto realizando un trabajo W(1-2) y aumentando
su entropía justo en QH/TH.
1
QH
TH
Expansión adiabática ( 2  3 )
El sistema se aísla térmicamente y se sigue expandiendo
adiabáticamente hasta que baja la temperatura a TL.
Mientras se expande realiza un trabajo W(2-3) a expensas
de la energía interna y se mantiene la entropía constante.
Compresión isotérmica a TH ( 3  4 )
El sistema se pone en contacto con un baño frío de
temperatura TL cediendo una cantidad de calor QH mientras
se comprime a la temperatura del baño y sufriendo un
trabajo W(3-4) y disminuyendo su entropía en QL/TL.
2
3
4
3
TH
TL
QL
TL
1
Compresión adiabática ( 4  1 )
El sistema se vuelve a aislar térmicamente y se sigue
comprimiendo adiabáticamente hasta que sube la temperatura a
Mientras se comprime sufre un trabajo
W(4-1) y se mantiene la entropía constante.
P
2
4
TH
TH.
TL
T
1
QH
TH
2
TH
W
4
QH
1
Q
TL
QL
3
2
TL
V
QL
4
S
3
S
S
Observaciones:
• El ciclo es reversible porque se realiza lentamente, el baño caliente está a una temperatura
infinitesimalmente mayor a TH y el frío está a una temperatura infinitesimalmente inferior a TL.
• En un ciclo completo el trabajo total es W=W12+W23+W34+W41 y el calor total es Q=QH-QL, y el
cambio de energía interna ∆U=0, por tanto: W=Q o [W12+W23+W34+ W41]=[QH-QL].
• Por ser reversible puede recorrerse en el otro sentido (como un refrigerador o bomba de calor).
Principios de Carnot:
Todas las maquinas térmicas que sigan un proceso reversible entre los mismos baños térmicos tienen
igual rendimiento.
El rendimiento de una máquina térmica que siga un proceso irreversible entre dos baños térmicos es
menor que el rendimiento de cualquier máquina térmica que siga un proceso reversible entre los dos
mismos baños
Si los principios de Carnot no se cumplen se violaría la 2ª Ley:
TH
QH
QH
-QH
W(I)-W(R)
W(R)
IRREV
REV
W(I)
-W(R)
QL(I)<QL(R)
QL(R)
QL(I)-QL(R)
-QL(R)
TL
TL
ESCALA TERMODINÁMICA DE TEMPERATURAS
T1
Del 2º principio de Carnot (o lo que es lo mismo la
2º ley) se deduce que el rendimiento sólo depende de
las temperaturas de los baños: η=η(TH, TL) ⇒ QH/QL =
función(TH,TL). Con tres maquinas siguiendo procesos
reversibles como indica la figura se llega a:
Q1/Q2=f(T1,T2),
Q2/Q3=f(T2,T3),
Q1
Q1
Q1/Q3=f(T1,T3).
Y como Q1/Q3=Q1/Q2 Q2/Q3 ⇒ f(T1,T3)=f(T1,T2)f(T2,T3)
Q2
La única forma para que se verifique esta igualdad es
que la función f sea de la forma: f(A,B)=F(A)/F(B), o
lo que es lo mismo que QH/QL=función(TH,TL)=
F(TH)/F(TL).
T2
Kelvin propuso una escala de temperaturas basada en
este resultado tomando la función más sencilla para
F(T)=T. Esta es la conocida escala absoluta de
temperaturas que se determina en parte por la
expresión: QH/QL = TH/TL. Pero esta expresión es sólo
una proporción entre temperaturas, hace falta otra
condición para determinar la escala completamente.
Para ello se asignó el valor 273.16K a la temperatura
del agua en el punto triple.
Q2
Q3
Q3
T3
MAQUINA TÉRMICA DE CARNOT
Es la que opera siguiendo un ciclo de Carnot
⇒ η = 1 – QL/QH = 1 – TL/TH < 1 ⇒
1 > η(cualquier ciclo Reversible) = 1 – TL/TH > η(cualquier ciclo IRReversible)
CALIDAD Y DEGRADACIÓN DE LA ENERGÍA:
TH≈TL
QH
TH>>TL
TH-TL pequeño
⇓
η pequeño
⇓
QH de poca
calidad
TL
TH-TL grande
⇓
η grande
⇓
QH de gran
calidad
QH
TL
De la relación entre las temperaturas de los baños y el rendimiento de una máquina de Carnot (y por
tanto de cualquier máquina térmica reversible) se llega a que la obtención de trabajo es mayor, para una
misma cantidad de calor cuanto mayor sea la diferencia de las temperaturas de los baños. Este mayor
calor se dice que es de mayor CALIDAD. La energía térmica que pasa de un baño a otro de menor
temperatura se DEGRADA en el sentido de que aun siendo la misma energía se podrá sacar menor
trabajo de ella.
LIMITES DE LOS COEFICIENTES DE OPERACIÓN DEL REFRIGERADOR Y LA BOMBA DE CALOR:
Como todo ciclo reversible, operando entre los mismos baños térmicos, tiene el mismo rendimiento (η)
que un ciclo de Carnot, también tendrá los mismos coeficientes de operación cuando se recorra el ciclo en
sentido inverso (refrigerador o bomba de calor según su uso) así que:
COP(refrigerador)
= 1/(QH/QL – 1) = 1/(TH/TL – 1).
COP(bomba de calor) = 1/(1 – QL/QH) = 1/(1 – TL/TH).
Estos son los coeficientes de operación mayores posibles (para cualquier ciclo reversible entre las mismas
temperaturas). Cualquier ciclo reversible tendrá coeficientes de operación menores.