GUIA PARA EL USO DE MATLAB PARTE 3 Symbolic Math Toolbox

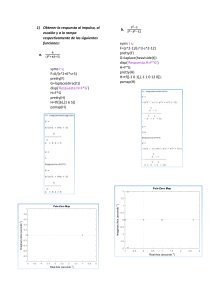
GUIA PARA EL USO DE MATLAB PARTE 3
Symbolic Math Toolbox
Las rutinas de matemática simbólica de MatLab son utilizadas para poder escribir
ecuaciones con variables genéricas sin necesidad de crear vectores.
Algunas ventajas del Symbolic Math Toolbox para el diseño y análisis de sistemas:




Las funciones y ecuaciones se pueden ingresar de manera simbólica, pudiéndose
utilizar tanto caracteres alfabéticos como numéricos. Por ejemplo puede ingresar
B = x^2+3*x+7, en lugar de B= [1 3 7]. También puede ingresar B=a*x^2+b*x+c.
Se pueden manipular algebraicamente y simplificar expresiones simbólicas.
Las transformadas de Laplace y Z se pueden ingresar y determinar sus inversas
en forma simbólica.
Las funciones se puede “imprimir con una mejor presentación” para mejor claridad
en la Command Window y entonces imprimirse en papel.
1. Definición de objetos simbólicos:
El inicio de cualquier cálculo simbólico requiere definir los objetos simbólicos, por ejemplo,
la variable de la transformada de Laplace (s) o la variable de tiempo (t).
Se utiliza el comando:
syms s t, siendo s y t la variables simbólicas.
Solamente en necesario definir los objetos que entran al programa, las variables
producidas por el programa no necesitan definirse. De este modo, si se está
determinando transformadas inversas de Laplace, solamente se necesita definir s puesto
que t resulta del cálculo.
2. Imprimir con mejor presentación:
Se utiliza el comando pretty(F), siendo F la función que se quiere imprimir en bonito.
Ejemplo 1:
syms s; %declaro variable simbólica
F=2/[(s+1)*(s+2)^2] %función de transferencia
pretty(F) %imprimo en bonito
f=ilaplace(F) %transformada inversa
pretty(f)
Vista en Command Window:

Sin pretty:
F=
2/((s + 1)*(s + 2)^2)

Con pretty:
2
---------------2
(s + 1) (s + 2)
3. Cambios en la apariencia de los resultados desplegados:






collect(F,s): Reúne los términos con coeficientes comunes de F, si coloco s le
aclaro que variable quiero que reúna.
expand(F): Expande los productos de factores.
factor(F): Factores de F.
simple(F): Determina la forma más sencilla de F con el menor número de
términos.
simplify(F): Simplifica F.
vpa(expression, places): Quiere decir precisión aritmética variable, este
comando convierte términos simbólicos fraccionarios en términos decimales con
un número específico de lugares después de la coma.
Ejemplo 2:
syms t;
f=2*exp(-t)-2*t*exp(-2*t)-2*exp(-2*t);%defino la función en el tiempo
'Función en el tiempo' %desplego etiqueta
pretty(f)
F=laplace(f);%calculo su transformada, tener en cuenta que Matlab da F(s)
%fracciones parciales
'Transformada'
pretty(F) %imprimir en bonito las fracciones paciales
F=simplify(F); %Combino las fracciones parciales
'Con simplify'
pretty(F)
Vista en Command Window:
Función en el tiempo
2
2
2t
------ - -------- -------exp(t) exp(2 t)
exp(2 t)
Transformada
2
2
2
----- - ----- - -------s+1 s+2
2
(s + 2)
Con simplify
2
---------------2
(s + 1) (s + 2)
Ejemplo 3:
syms t;
f=3/16-3/16*exp(-t)*[cos(2*t)+(1/2)*sin(2*t)];
F=laplace(f);
'Transformada'
pretty(F)
F=vpa(F,3);
'Precisión aritmética variable con pretty'
pretty(F);
Vista en Command Window:
Transformada
3
3 (s + 1)
---- - ----------------- 16 s
2
16 ((s + 1) + 4)
3
----------------2
16 ((s + 1) + 4)
Precisión aritmética variable con pretty
0.188
----- s
0.188
---------------- 2
(s + 1.0) + 4.0
0.188 (s + 1.0)
---------------2
(s + 1.0) + 4.0
Ejemplo 4:
syms x y z;
a=collect(((log(x)+2*x)*(x+2)))
b=collect((2*x+y)*(x^3+5*y+3),y)
d=expand((z+3)*(z+6)*(z-4))
e=x^3+x^2+3*x+x*y+x*z;
f=factor(e)
g=sin(x)^2+cos(x)^2;
h=simple(g)
Vista de Command Window
a=
2*x^2 + (log(x) + 4)*x + 2*log(x)
b=
5*y^2 + (x^3 + 10*x + 3)*y + 2*x*(x^3 + 3)
d=
z^3 + 5*z^2 - 18*z - 72
f=
x*(x^2 + x + y + z + 3)
h=
1
4. Funciones transferencia con la regla de Cramer:
La regla de Cramer da la solución de un sistema de ecuaciones lineales con el mismo
número de incógnitas que de ecuaciones, el determinante de la matriz de los coeficientes
debe ser distinto de cero.
Un sistema de ecuaciones lineales tiene la forma Ax=B, siendo A la matriz formada por
los coeficientes de las incógnitas, x es el vector de las incógnitas y B es un vector que
contiene las entradas.
Xk= det(Ak)/det(A), siendo Ak la matriz formada al reemplazar la k-ésima columna de la
matriz A con elvector de entrada B
Ejemplo 5:
Dado el siguiente circuito obtener la función de transferencia (I2/V) aplicando regla de
Cramer.
Solución:
Obtenemos el sistema de ecuaciones:
(R1+Ls) I1 - Ls
I2 = Vi
-Ls
I1 + (Ls+R2+1/Cs) I2 = 0
G( s) 
LC.s 2
( R 2  R1)CL.s 2  ( R1R2C  L).s  R1
En MatLab:
syms Vi R1 L R2 C s;
A2=[(R1+L*s) Vi;-L*s 0];
A=[(R1+L*s) -L*s; -L*s (L*s+R2+(1/(C*s)))];
I2=det(A2)/det(A)
G=I2/Vi;
G=collect(G,s)
pretty(G)
Vista en Command Window
I2 =
(C*L*Vi*s^2)/(R1 + L*s + C*L*R1*s^2 + C*L*R2*s^2 + C*R1*R2*s)
G=
((C*L)*s^2)/((C*L*R1 + C*L*R2)*s^2 + (L + C*R1*R2)*s + R1)
2
(C L) s
------------------------------------------2
(C L R1 + C L R2) s + (L + C R1 R2) s + R1
5.
Ingreso de funciones de transferencia complicadas:
Cuando se tiene funciones de transferencia complicadas, se puede hacer distributiva en
tres pasos.
Ejemplo 6:
En MatLab:
syms s;
G=(54*(s+27)*(s^3+52*s^2+37*s+73))...
/(s*(s^4+872*s^3+437*s^2+89*s+65)*(s^2+79*s+36));
[numg,deng]=numden(G);
numg=sym2poly(numg);
deng=sym2poly(deng);
'Función transferencia reordenada'
Gtf=tf(numg,deng)
'Función de transferencia en forma de ceros y polos'
Gzpk=zpk(Gtf)
Vista en Command Window
Función transferencia reordenada
Transfer function:
54 s^4 + 4266 s^3 + 77814 s^2 + 57888 s + 106434
--------------------------------------------------------------------s^7 + 951 s^6 + 69361 s^5 + 66004 s^4 + 22828 s^3 + 8339 s^2 + 2340 s
Función de transferencia en forma de ceros y polos
Zero/pole/gain:
54 (s+51.31) (s+27) (s^2 + 0.6934s + 1.423)
-------------------------------------------------------------------s (s+871.5) (s+78.54) (s+0.558) (s+0.4584) (s^2 - 0.05668s + 0.1337)
6. Graficación:
Se pueden hacer gráficas bidimensionales con objetos simbólicos, se utiliza la instrucción
ezplot(f, [xmin xmax]), si no se colocan los valores [xmin xmax], MatLab grafica
automáticamente entre -2*pi y 2*pi.
Ejemplo7:
En MatLab:
syms x;hold on;
ezplot(abs(x), [-3 3]);
ezplot(x^2, [-3 3])
figure
subplot(2,1,1)
ezplot(cos(x))
subplot(2,1,2)
ezplot(x^3)